基于约束的MLEM 图像重建算法

张 斌，王 英，艾宪芸，魏 星

（防化研究院 国民核生化灾害防护国家重点实验室，北京 102205）

编码孔γ相机作为一种新型的核辐射监测设备，能通过生成可视化图像使操作人员快速识别并定位视野中放射源目标，可极大缩短作业时间，减少人员受到的照射剂量，在环境辐射监测、核废料处理、通关口岸货物放射性检测等领域具有广泛应用。与普通光学相机不同的是，编码孔γ相机并不能直接对放射性物质进行成像，而要在成像过程中进行所谓的“编码”和“解码”：放射源发射出的γ射线经过编码孔准直器调制后在探测器上形成投影图像，经过离散采样后传入计算机中，再通过特定图像重建算法恢复出可视化的放射性强度二维分布图像。线性算法和迭代算法是编码孔γ相机图像重建中的两类主要算法。线性算法如交叉相关法［1］等具有算法简单、计算速度快的优点，但在投影图像受噪声影响较大的情况下重建图像质量较差。以MLEM 算法为代表的迭代算法能很好地抑制噪声，对不完全数据亦能重建，然而MLEM 算法的缺点是收敛速度慢，且在投影图像中包含噪声较大时，迭代次数过高会使重建图像中噪声随迭代次数的增加而加剧。针对这种情况，本文将直接解调法（direct demodulation method）［2］思想应用于MLEM 算法中，在迭代过程中加入先验物理约束条件，并以交叉相关法计算结果作为迭代初始值，加快MLEM迭代的收敛速度，提高重建图像的质量。

1 算法介绍

1.1 二维MLEM 算法

极大似然估计法是根据极大似然准则来求解似然函数中未知参数的一种参数估计法，解决这类问题的基本方法是求偏导解方程，但在图像重建中，未知参数众多，计算如此繁复的方程组几乎是不可能的。用期望最大化法实现极大似然图像重建最早由Shepp等［3］于1982年提出，最终形成MLEM 算法。期望最大化法以迭代法为基础，通过迭代更新方程组中参数的估计值，使似然函数不断增大，直至逼近其最大值，最终获得极大似然参数的估计值，这样就把原本极其复杂的极大似然估计问题转化为简单的求解期望值最大化过程。MLEM 算法是一种基于泊松统计模型的贝叶斯后验概率最大的图像复原方法，该算法以符合实际情况的模型为基础，重建图像的分辨率和本底噪声抑制能力较传统线性算法提升很多，因此在核医学等领域得到了广泛应用。编码孔γ相机图像重建中的二 维MLEM 算 法［4］可 表 示 为：

式中：“＊”表示卷积运算；“⊗”表示相关运算；fk（x，y）为第k次迭代后的图像估计值；p（x，y）为γ射线透过编码板后在探测器上的实际投影图像；h（x，y）为编码函数。

1.2 基于约束的MLEM 算法（DD-MLEM）

在理想无噪声的情况下，MLEM 迭代的解是收敛的，重建出的图像与目标图像最终趋于一致。但实际成像中所测得的投影图像数据中必然包含有各种噪声，这使得迭代不能完全收敛：在迭代次数较低时，图像质量逐渐提高；当迭代次数超过某一值后，图像质量反而变差。这主要是因为MLEM 迭代的修正准则是要求投影估计值与实测投影越接近越好，但对于重建出的图像却无任何约束。为改善MLEM 迭代在实际使用中的收敛性，本文借鉴了直接解调法思想来优化MLEM算法，提高重建图像质量。直接解调法最初是一种应用于高能射线天文望远镜中的成像方法，该方法与其他算法的显著区别是利用先验的物理知识作为约束条件，并添加到迭代求解的过程中。在迭代过程中加入的物理约束是对于被测目标的已知信息，所以使用这种方法不仅能有效抑制投影数据中本底噪声的影响，使迭代收敛性得到明显改善，而且最终重建出的图像较单纯使用MLEM 算法能更加趋近于真实情况。

实际成像的图像重建过程中主要使用本底约束条件：若fk（x，y）＜fb（x，y），则令fk（x，y）＝fb（x，y），其中fb（x，y）为本底约束值。如果本底噪声水平较低，可选择fb（x，y）＝0；如果本底噪声较强，为了提高成像灵敏度，需先得到背景辐射强度分布db，db可取估计值或由实际观测数据中剔除放射源影响后获取，然后再求解调制方程Hfb＝db（H 为系统的传递函数），最终得到迭代的本底约束fb。

此外，在进行图像重建迭代时，一般选择均匀的灰度图像作为迭代的初始值，本文仿真中采用了交叉相关法的重建结果作为迭代的初始值，实验证明这种方法可在一定程度上加快迭代收敛速度。交叉相关法的计算过程可由下式表示：

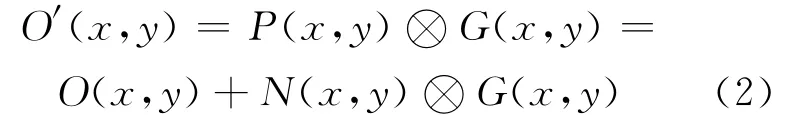
其中：O′（x，y）为对放射源目标O（x，y）的估计图像；P（x，y）为投影图像；G（x，y）为解码函数（由成像系统的编码函数决定）；N（x，y）为噪声项。

由此，本文中基于约束的MLEM 算法计算过程可分为以下几个步骤：

1）令k＝0，初始化fk（x，y）（一般将初始化图像f0（x，y）设置为各像素相等的均匀灰度图像，本文中将其设置为交叉相关法的重建图像）；

2）应用式（1）计算fk＋1（x，y）；

3）对fk＋1（x，y）施加一定的物理约束条件；

4）根据一定的准则判断迭代重建结果是否达到收敛要求，若已达到要求，则停止迭代；若未达到要求，则令k＝k＋1，将更新后的fk（x，y）再次转入执行步骤2。

2 仿真实验与分析

2.1 仿真条件

仿真实验以19×19的改良均匀冗余阵列（modified uniformly redundant array，MURA）编码孔准直器为基础，成像系统参数选择为：物距500mm，像距80mm，编码板小孔单元边长2mm，编码板厚度5mm，材料为钨。探测目标为位于视野中心轴线上的1 个点源，活度为1 MBq，能量为662keV。由上述条件模拟的理想点源图像和投影图像如图1所示。迭代时在模拟投影图像中加入随机高斯噪声，得到含噪声的投影数据进行图像重建。

2.2 评价准则

在对比两种算法重建图像的效果时，有时通过主观观察很难判断，为了验证所提出方法的有效性，采用归一化均方误差（normalized root mean square error，NRMSE）衡量算法的收敛速度，用相关系数（correlation coefficient，CC）评价重建图像的质量，它们的定义［5］分别为：

式中：xij和分别为真实图像和重建图像的像素灰度值和分别为真实图像和重建图像的平均像素灰度值。归一化均方误差表示重建图像与真实图像的接近程度，其值越小代表重建效果越好，而相关系数评价的是重建图像与真实图像的相似度，其值越大表示重建图像与真实图像越接近。

图1 模拟的点源图像和投影图像Fig.1 Simulated point source image and projection image

2.3 仿真结果分析

在实际成像中，当成像系统计数率足够高时，投影图像中叠加的噪声趋近于高斯分布。仿真实验采用了这一噪声模型，在DD-MLEM迭代中构造基于高斯分布的本底并进行图像重建，将重建后的背景图像作为迭代约束条件，采用交叉相关法计算结果作为迭代初值。图2和图3分别为MLEM 算法和DD-MLEM 算法迭代次数n＝30、90、270时的重建图像。通过直接观察可看出，在选取合适迭代次数的情况下，两种算法均能得到相对较好的重建效果，但在迭代次数过高时，MLEM 算法重建的图像局部区域噪声被放大，原本光滑的图像出现离散的斑点，在视觉上难以接受；而DD-MLEM 迭代则不然，在过高迭代次数下依然能很好地控制图像噪点，保持图像的可辨识性。

图2 MLEM 迭代重建图像Fig.2 Reconstructed image by MLEM iteration

图3 DD-MLEM 迭代重建图像Fig.3 Reconstructed image by DD-MLEM iteration

为进一步评价重建图像的质量，利用式（3）和式（4）给出的评价准则对两种算法的重建图像效果进行定量分析。图4示出两种算法所重建图像的归一化均方误差随迭代次数的变化情况。由图4a可看出，在迭代次数相对较低时，两种算法的归一化均方误差均随迭代次数的增加而减小，重建图像质量不断提高，但DD-MLEM算法的收敛速度显然要快得多；当迭代次数继续增加时，由图4b可知，MLEM 算法的归一化均方误差在达到一最小值后迅速增大，重建图像的质量也随之变差，而DD-MLEM 算法在迭代次数过高的情况下归一化均方误差只是略微变大，重建图像的质量仍能保持得比较好。图5示出两种算法的相关系数随迭代次数的变化情况，可更加明显地看出DD-MLEM 算法收敛速度不但更快，而且提高了算法最佳迭代次数，重建图像的质量也优于原算法。在迭代次数过高时，MLEM迭代的重建图像质量迅速下降，而DD-MLEM 迭代则能将图像质量一直保持在较高水平上。

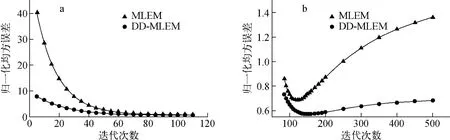
图4 归一化均方误差随迭代次数的变化Fig.4 NRMSE of two algorithms versus iteration time

图5 相关系数随迭代次数的变化Fig.5 CC of two algorithms versus iteration time

3 结论

在编码孔γ相机图像重建中，MLEM 迭代算法能较为有效地抑制统计噪声，较传统交叉相关法恢复出的图像质量要高得多，但缺点是收敛速度较慢且迭代次数过高时图像质量变差。本文提出一种基于约束的MLEM 算法，在迭代过程中加入物理约束条件，并用交叉相关法计算值作为迭代初始值。实验结果证明，DD-MLEM 算法不仅收敛速度加快，且重建图像质量和迭代的收敛性与收敛速度均得到显著提高。使用这种方法可更加充分地利用被观测目标的已知信息，从而有效抑制由于噪声等因素所引起的迭代解的病态特征，相比仅用迭代法或相关法能更好地重建出反映真实情况的图像。值得注意的是，此方法重建图像的质量对约束条件有较强的依赖，对于复杂的测量环境，应根据现场实际情况选取更为合理的物理约束条件以保证成像质量。

［1］ 何会林，董永伟，吴伯冰，等.空间硬X 射线编码孔成像望远镜样机的研制及初步实验结果［J］.高能物理与核物理，2007，31（5）：437-441.HE Huilin，DONG Yongwei，WU Bobing，et al.A prototype of spatial hard X-ray coded aperture imaging telescope and the primary laboratory experimental results［J］.High Energy Physics and Nuclear Physics，2007，31（5）：437-441（in Chinese）.

［2］ 李惕碚，吴枚.高能天文中成像和解谱的直接方法［J］.天体物理学报，1993，13（3）：215-224.LI Tibei，WU Mei.The direct method for spectral and image restoration in high energy astronomy［J］.Acta Astrophysica Sinica，1993，13（3）：215-224（in Chinese）.

［3］ SHEPP L A，VARDI Y.Maximum likelihood restoration for emission tomography［J］.IEEE Transactions on Medical Imaging，1982，1（2）：113-122.

［4］ MU Z P，LIU Y H.Aperture collimation correction and maximum-likelihood image reconstruction for near-field coded aperture imaging of single photon emission computerized tomography［J］.IEEE Transactions on Medical Imaging，2006，25（6）：701-711.

［5］ 何佳伟，刘东升，桂志国.可变有序子集PML 算法在PET 中的应用［J］.中北大学学报：自然科学版，2010，31（6）：646-650.HE Jiawei，LIU Dongsheng，GUI Zhiguo.Application of modified subsets PML algorithm to PET image reconstruction［J］.Journal of North University of China：Natural Science Edition，2010，31（6）：646-650（in Chinese）.