凸度测量过程中点扩展函数的蒙特卡罗模拟与解析表达研究

胡克敏，吴志芳，苗积臣，谈春明

（清华大学 核能与新能源技术研究院 核检测技术北京市重点实验室，北京 100084）

清华大学核能与新能源技术研究院研制成功的凸度测量系统是利用X 射线法高精度测量板带材（钢板）横断面厚度分布，进而计算出板带材凸度、楔度及中心线厚度等参数的大型多功能轧钢自动化装备。为保证±0.1%的测量精度，对测量过程中康普顿散射的影响分析及校正是一必需的关键环节。凸度测量系统中散射的影响主要分为两部分：1）被测钢板自身康普顿散射造成的影响，也是散射影响的主要原因；2）凸度测量系统各结构部件造成的散射影响，此部分的影响较小，且错综复杂，较难定量分析。本文主要针对第一部分即钢板自身的散射影响作深入研究。

目前国内外散射校正的方法［1］包括3类：1）硬件方法，基本原理为采用物理方法消除或减少进入探测单元的散射射线来实现；2）软件较正方法，包括卷积法、反卷积法、蒙特卡罗（MC）方法、理想模型估计等；3）混合校正方法，通过散射校正板、频率调制［2］等硬件的设计取得散射影响分布，再融合软件方法进一步得到精确信息的方法。本文采用蒙特卡罗方法模拟计算凸度测量系统中点扩展函数（PSF）与板材厚度、射线能量间的关系曲线，采用非线性拟合方法确定PSF理论模型参数，得到单能射线下凸度测量系统的PSF理论公式，为进一步实现凸度测量系统的散射校正奠定基础。

1 点扩展函数的蒙特卡罗模拟计算［3］

1.1 计算模型

以凸度测量系统为参照，模拟计算能量为E的δ脉冲射线垂直照射厚度为D 的铁板，探测面至被测钢板下表面的距离H 为60cm（图1）。

图1 PSF MC模拟计算模型Fig.1 MC simulation model of PSF

本文采用MCNP 软件对上述模型在不同射线能量、不同铁板厚度情况下的PSF 进行相关计算分析。另外，本文所述的PSF仅指到达探测器的散射光子数占射线源光子总数的概率（或称散射光子的贡献），不包括透射光子。

1.2 射线能量、钢板厚度对PSF的影响

参照凸度测量系统，射线能量范围设置为0～0.3MeV，测量厚度范围为0～16mm，探测面到钢板下表面的距离为60cm。由射线与物质的相互作用宏观经验公式可得到透射光子概率为：

其中：μ 为线性衰减系数；D 为钢板厚度；μm 为质量衰减系数；Dm为质量厚度。

1）当入射射线为单一能量时，PSF 随射线能量的变化

钢板厚度设置为8mm，分别模拟计算出不同能量的射线作用下，探测器接收的散射、透射光子概率分布情况，计算结果如图2～4所示。

图2 不同射线能量下PSF沿探测面的分布曲线Fig.2 Distribution curve of PSF with detection surface under different ray energy

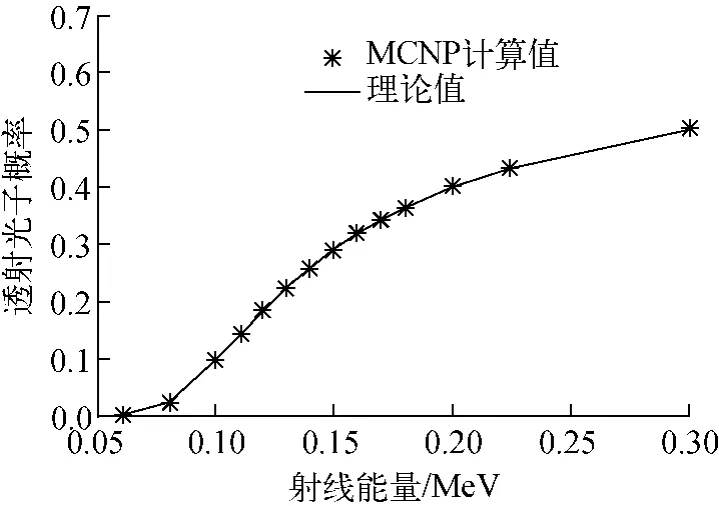
图3 透射光子概率随射线能量的变化Fig.3 Transmission probability vs ray energy

由图2可看出，随射线能量从60keV 增加到300keV，PSF的幅值逐渐增大，但增长幅度渐缓，且曲线形状保持轴对称不变。从物理分析的角度，虽然随着能量的增加，康普顿散射的截面Σs减小，发生散射的概率减小，但由于低能段光子更易发生光电效应和多次散射，被衰减吸收的较多，导致最终出射的散射光子减少，因此PSF 的幅值随能量的增大稍有增大。由图3可看出，透射光子的概率随能量的变化呈多次曲线形状，且MCNP 模拟计算值与理论值完全符合。由图4可看出，探测位置离入射中心点越近，散射光子概率越大，即所接收发生散射的光子越多；当射线能量在0.06～0.18 MeV之间时，E 越大，散射量越大，也呈多次曲线形状。

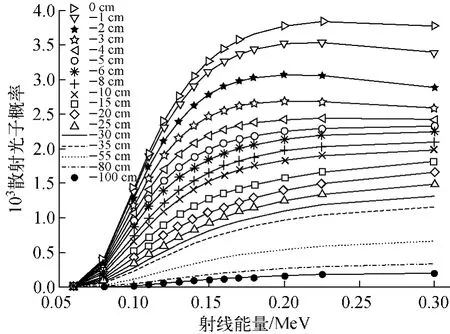
图4 不同探测位置处散射量随射线能量的变化曲线Fig.4 Curve of scattering probability vs ray energy at different detection positions

2）单能射线与连续能谱射线作用下PSF的计算

实际上，凸度测量系统所用的X 射线源具有连续能谱，因此，研究在连续能谱射线作用下PSF的计算很有必要。但直接对连续能谱射线进行分析计算较困难，且管电压和管电流不稳定，也会造成能谱的较大差值，因此，本文设想采用多个单能计算结果的线性组合来代替对整个连续能谱的分析计算，即首先选择若干典型的单能射线，分别代表整个连续能谱的不同能段；然后，分析计算出每个单能射线下的MCNP模拟结果（如散射光子分布）；再将这些单能射线下的计算结果进行加权求和，作为整个连续能谱作用下的MCNP计算结果。

针对最大能量为180keV 的X 光机连续能谱，本文选取一简单模型（仅选4个单能值）进行分析（表1），钢板厚度取8mm。分别计算单能情况下加权求和的结果和直接用整个连续能谱计算的结果（图5、6），可看出，两者基本吻合，但存在约10%的差距，对8mm 厚度钢板，10%的差距对散射的影响在万分之几范围，小于凸度测量系统千分之一的精度要求，且通过选用更多的单能射线及优化权重因子，可获得更好的模拟结果，因此，在实际应用中，可考虑用单能的线性组合代替实际能谱计算。

表1 能谱分段数据Table 1 Division data of energy spectrum

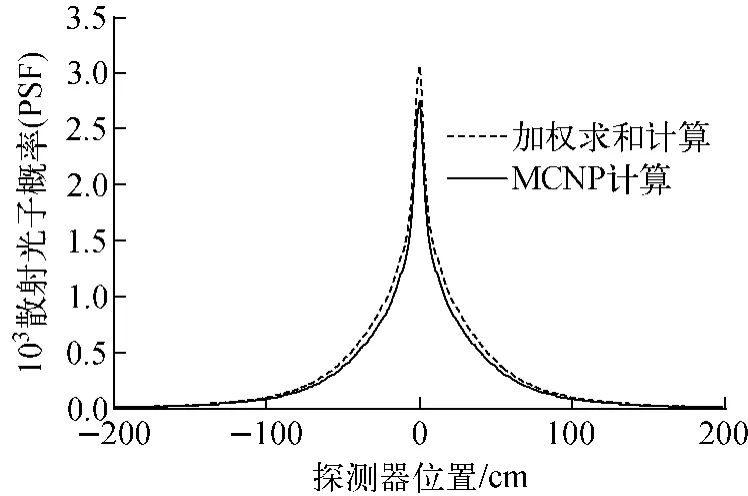
图5 散射光子概率分布结果对比Fig.5 Contrast of scattering photon probability distribution

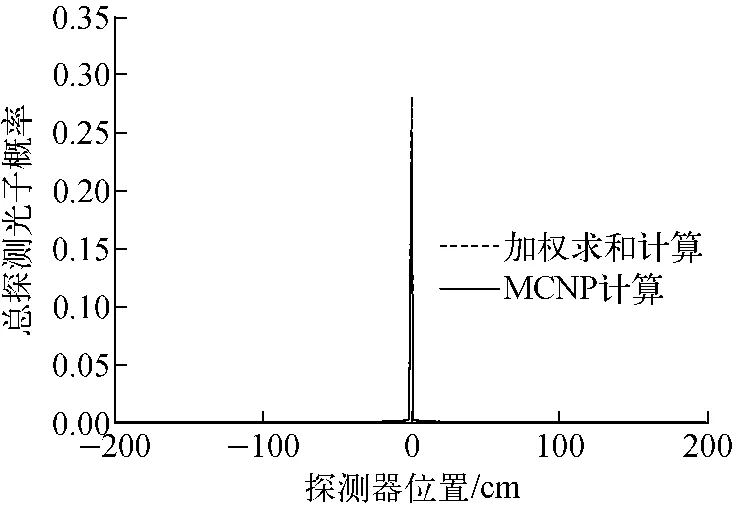
图6 总探测光子概率分布结果对比Fig.6 Contrast of total detection photon probability distribution

3）PSF随钢板厚度变化分析

选用射线能量为0.18 MeV，分别计算钢板厚度D 为1～16mm 的PSF，计算结果如图7～9所示。由图7 可看出，随着铁板厚度从1mm增大到10mm，散射的PSF（即散射光子的概率分布）逐渐增大，且随着厚度的增加，PSF增大的幅度却逐渐减小，主要原因是随着厚度的增大，光子发生多次散射而被吸收的比例增多，导致散射后最终出射的光子减少。由图8可看出，MCNP模拟计算的透射概率和理论值较吻合，符合射线衰减规律。由图9可看出，在0.18 MeV 射线下，PSF 随钢板厚度D的增大先增大后减小，距入射中心点越近，幅值越大，散射光子越多。

图7 PSF沿探测面的分布曲线Fig.7 Distribution curve of PSF with detection surface

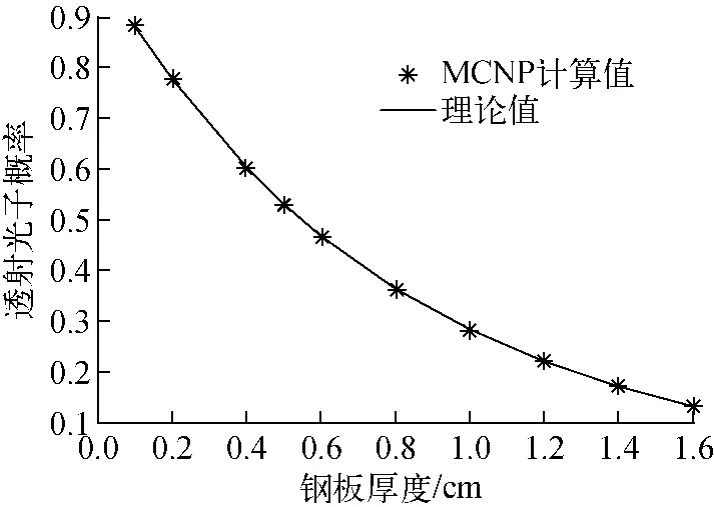
图8 透射光子概率随钢板厚度的变化Fig.8 Transmission probability vs steel thickness

2 PSF的解析表达

上述PSF 的分析研究是基于数值表达的，若能把PSF用解析形式表达出来，将更有利于实际应用。通过对PSF的曲线形状分析可知，其近似于高斯分布，若用1 个高斯函数表述，其结果与实际偏差较大，因此，本文选择采用两个高斯函数的线性组合来拟合PSF，这一点在SPECT、PET 散射校正中已得到验证，在中子成像中也有较好的效果［4］。用两个高斯函数的线性组合模型来近似PSF，其二维形式［5］为：

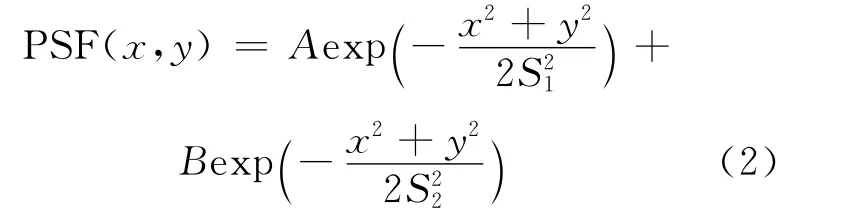
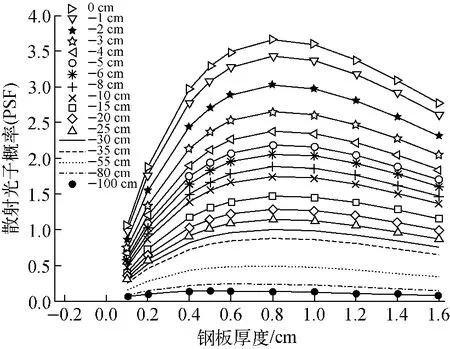
图9 不同探测位置处散射量随钢板厚度的变化曲线Fig.9 Curve of scattering probability with steel thickness under different detection positions

对PSF沿y 轴方向积分，得到PSF的一维积分形式为：

其中，C1、C2、S1、S2均为参数。

对于理想单能准直射线束，参数C1、C2、S1、S2与射线能量、被测钢板性质、被测钢板厚度、被测钢板到探测面的距离（空气隙）相关。

针对凸度测量系统，探测器到钢板下表面的距离为设定值60cm，假定射线能量为180keV，则参数C1、C2、S1、S2仅与钢板厚度相关，即：

通过蒙特卡罗方法模拟，分别计算出厚度为1～16mm 的钢板PSF的结果，然后采用非线性最小二乘原理和方法，用式（5）进行曲线拟合，求出分别对应于不同厚度钢板的参数C1、C2、S1、S2的最佳拟合估计值（表2），均方差R 越趋近于1，相干系数RMSE 越趋近于0，所得拟合值就越好。各参数与钢板厚度的曲线关系如图10所示。对各曲线采用多项式拟合的方法，可得到凸度仪系统在射线能量为180keV 时PSF各参数与钢板厚度的关系式，据此，就可计算出任意钢板厚度下的PSF分布，从而进行散射校正，提高测量精度。

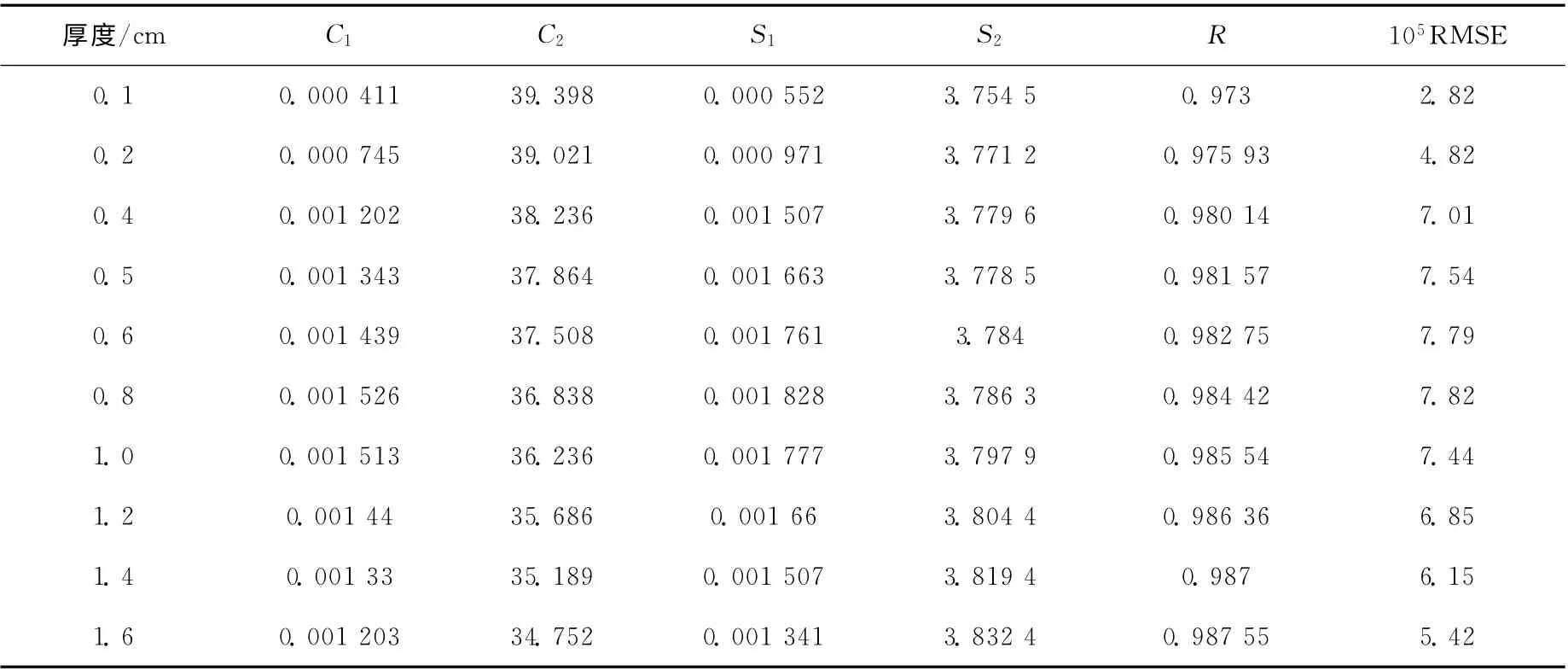
表2 参数C1、C2、S1、S2 拟合估计值及其均方差和相干系数Table 2 Fitting parameters，mean square error and correlation coefficient

图10 各参数与钢板厚度的拟合曲线Fig.10 Fitting curve of parameters and steel thickness

3 结论

本文通过蒙特卡罗模拟方法，研究了钢板凸度测量中散射影响的PSF及其影响因素，在此基础上，采用双高斯函数模型，对PSF 的解析表述方法进行了分析探究，给出180keV 射线情况下点扩展函数的解析表达形式，这对钢板凸度测量中的散射校正问题提供了技术支持。

［1］ 张峰，闫镔，李建新，等.工业X-CT 散射校正技术综述［J］.CT 理论与应用研究，2009，18（4）：34-43.ZHANG Feng，YAN Bin，LI Jianxin，et al.Review of scatter correction on X-ray industrial computed tomography［J］.CT Theory and Applications，2009，18（4）：34-43（in Chinese）.

［2］ ZHU L，BENNETT N R.Scatter correction method for X-ray CT using primary modulation：Theory and preliminary results［J］.IEEE Transactions on Medical Imaging，2006，25（12）：1 573-1 587.

［3］ 裴鹿成，张孝泽.蒙特卡罗方法及其在粒子输运问题中的应用［M］.北京：科学出版社，1980.

［4］ 魏彪，马晓昕，金炜，等.定量中子数字成像散射校正的蒙特卡罗模拟［J］.强激光与粒子束，2008，20（9）：1 545-1 550.WEI Biao，MA Xiaoxin，JIN Wei，et al.Monte-Carlo simulation of scattering correction forquantitative neutron imaging system［J］.High Power Laser and Particle Beams，2008，20（9）：1 545-1 550（in Chinese）.

［5］ NUYTS J，BOSMANS H，SUETENS P.An analytical model for compton scatter in a homogeneously attenuating medium［J］.IEEE Transactions on Medical Imaging，1993，12（3）：421-429.