基于改进爬山法的带电粒子圆径迹重建

牛莉博，李玉兰，傅楗强，黄 孟，何 彬，李元景

（1.清华大学 工程物理系，北京 100084；2.第二炮兵工程大学102教研室，陕西 西安 710025；3.清华大学 粒子技术与辐射成像教育部重点实验室，北京 100084）

径迹探测器是一重要的电离辐射探测器，被广泛应用于大型物理实验、核技术及应用等领域，基于时间投影室（TPC）的径迹探测器是目前使用最为广泛的径迹探测器之一［1-3］。TPC的基本原理为：当带电粒子经过TPC 灵敏体积时，使TPC 工作气体电离产生电子-离子对，电子在TPC 内部均匀电场作用下，向读出端盖漂移并产生雪崩放大。电子信号由按一定规则排列的若干读出盘读出，读出盘的位置信息确定了带电粒子x-y 方向的位置，而z 方向的位置由z＝vD（t1-t2）确定（vD为电子在电场中的漂移速度；t1为带电粒子穿过TPC 的时间，由外部时间探测器的触发信号给出；t2为电子到达读出端面的时间）。根据读出盘的击中信息重建带电粒子的飞行径迹是TPC 数据分析的重要步骤，在均匀磁场情况下，带电粒子的径迹是1条空间螺旋线，其在二维读出平面上的投影为圆形。圆径迹重建的任务为：对于给定的1 组二维读出平面上的击中点（xi，yi）（i＝1，2，…，n），通过一定的算法判断这些击中点是否来自于同一圆径迹，即这些击中点是否由同一带电粒子产生；若这些测量点由同一带电粒子产生，则对这些击中点进行拟合得到该圆径迹参数，即圆心（a，b）和半径R 的拟合值。

霍夫变化是一种简单有效的径迹重建方法，在粒子径迹重建算法中得到了广泛使用［4-6］。然而，由于霍夫变换需将参数空间进行离散化，随参数空间维数的增加，计算量将急剧增加，计算速度变慢。文献［7］指出，霍夫变换法已很难满足对圆径迹的识别与检测。爬山法最早由Yager和Filev［8-9］提出，是一有效的快速聚类算法。与霍夫变化一样，传统的爬山法也需将参数空间进行网格化，对高维数据的聚类速度急剧下降。而改进爬山法则使用数据点替代网格点，在数据点构造密度函数替代在网格点构造山峰函数，通过寻找密度函数最大值以确定参数拟合结果，可极大提高计算速度，对高维数据的聚类分析具有良好适应性。本文通过空间映射将圆径迹寻迹问题转化为寻找参数空间上的聚类中心问题，使用改进爬山法获得圆径迹的参数拟合值，并给出不同情况下圆径迹拟合参数的精度。

1 方法

1.1 爬山法

假设有n个数据点｛x1，x2，…，xn｝，每个数据点是p 维的，即xj∈Rp（j＝1，…，n）。传统爬山法中，首先在数据空间中定义1组网格点｛Ni｝，Ni∈RF，聚类中心被固定在这些网格点上。然后在每个网格点上定义山峰函数如下：

其中，d（xj，Ni）为数据点xj和网格点Ni之间的距离。显然，对于拥有较多临近点的网格点，其山峰函数值较大，参数α决定临近区域的大小。具有大的山峰函数值M1（Ni）的网格点Ni成为聚类中心的潜在可能性大。于是，可将具有最大峰值的网格点设定为第1个聚类中心，即可通过以下目标函数找到第1个聚类中心N＊1：

对于具有多个聚类中心的情况，在寻找下一聚类中心前，有必要消除上一网格点对下一聚类中心的影响。在找到第k-1个聚类中心N＊k-1后，估计第k个聚类中心的计算公式如下：

其中，k＝2，3，…，且有：

式（4）为峰值调整方程，参数γ决定了消减已提取聚类中心点峰值影响的临近区域的大小。通过式（3）和（4）的迭代可得到新的聚类中心。

1.2 改进爬山法

显然，爬山法的计算时间随数据维度的增加而急剧增加，Chui［10］用数据点代替网格点来改进原始的爬山算法。在此基础上，Yang等［11］对山峰函数和峰值调整方程进行了修改，进一步减小算法的计算时间。在改进的爬山算法中，考虑用核密度估计每个数据点向xi的密度：

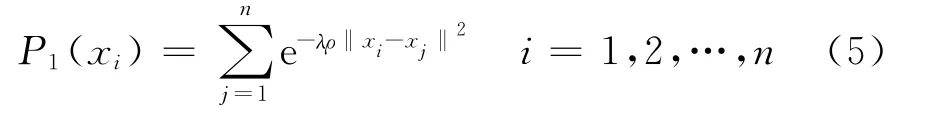
且

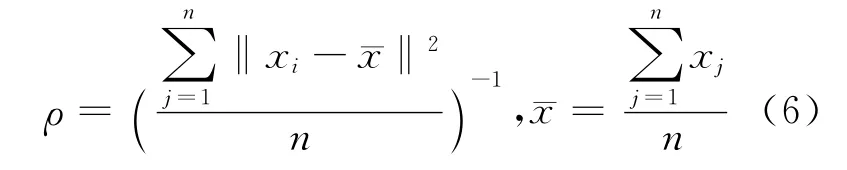
式中：参数ρ为归一化项；参数λ可由自相关有关算法得到，或由实验者给定。于是第1个聚类中心估计公式为：

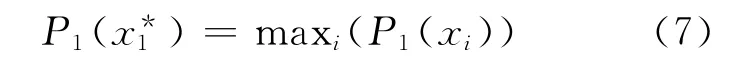
在估计出第k-1个聚类中心后，用改进的山峰调整算法调整下一轮的山峰：

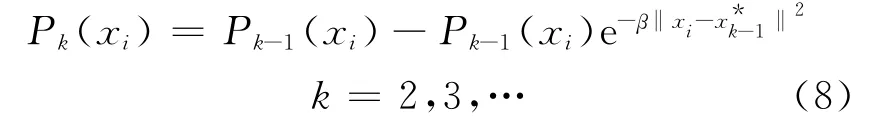
在调整后的密度中，具有最高密度值Pk（xi）的那个数据点即为所要提取的第k个聚类中心：

通过式（8）和（9）的不断迭代，可提取出新的聚类中心。

1.3 空间映射

尽管改进爬山法能很好估计出聚类中心，但由于初始测量点并不具备聚类特性，无法直接应用于圆径迹的重建。为能将改进爬山法应用于圆径迹的重建，首先需对击中点进行变换，即将测量得到的二维坐标数据（xi，yi）转变为参数空间中的参数值，该参数值与对应圆径迹参数有关。圆方程可如下表示：

式中，d＝R2-a2-b2。由于平面上任意3个不共线的点将确定1个圆，且该圆的圆心和半径可按下式计算得到：

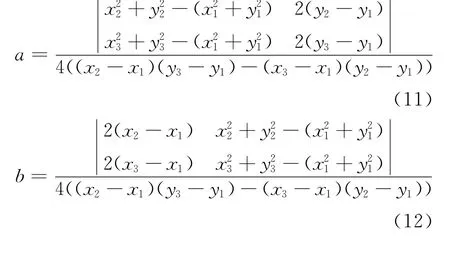
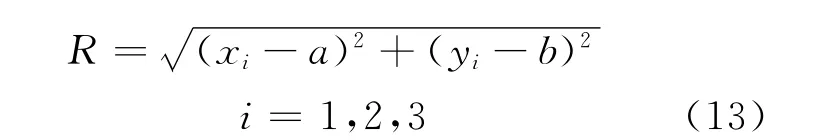
这样，对所有（xi，yi）中任意3个不共线的测量点组合便可得到个参数值（aj，bj，Rj）。由于测量点（xi，yi）来自于相同的圆径迹，因此由测量点空间映射得到的参数值（aj，bj，Rj）在参数空间里面形成聚类。图1a为有两条圆径迹并包含噪声点的原始测量数据分布，图1b、c、d分别为测量点空间映射后所得参数值在a-b、a-R、b-R 平面上的投影。由图1可知，参数值在参数空间中存在聚类中心，且该聚类中心在参数空间中的位置即为圆径迹参数的拟合值。

2 算法性能

2.1 单圆径迹重建

计算中选取的圆径迹的真实参数为圆心（a，b）＝（4，5），半径R＝2，使用该参数随机产生的击中点数目分别为8、12和16。在实际探测器中，测量点（xi，yi）的坐标存在测量误差，模拟中随机产生的测量点（xi，yi）到圆心的距离服从高斯分布，该分布的均值为半径R，方差分别为R的5%、10%和15%。除此之外，模拟数据还随机产生了一些噪声点，噪声点数分别选为数据点的50%、25%和0%，噪声点的（xi，yi）坐标均匀分布在［0，10］区间上。图2为上述模拟数据中的1个事例，图2a为随机产生的原始数据，有效数据点为20个，噪声数据点为10个，即50%的噪声数据点，（xi，yi）坐标的测量不确定度为10%的R；图2b为数据点空间映射产生的参数值在参数空间a-b平面上的投影；图2c为密度函数值在参数空间a-b 上的投影；图2d为参数空间上的密度函数值，密度函数值的大小用彩虹图表示，数值由大到小依次由红色到蓝色表示。

式（5）中参数λ 的选择决定了改进爬山法是否能正确获得拟合参数以及参数的拟合精度，文献［11］指出λ 的选择可通过自相关的有关算法给出或由实验者设定。实际上参数λ的选择与参数空间中的数据结构有直接关系，模拟研究发现对于上述模拟数据，当λρ＝50时，改进爬山法具有良好的适用性，因此本文所有计算均选择λρ＝50。在实际的径迹重建中，应当根据探测器的尺寸、圆径迹的分布及噪声水平等探测器性能参数合理设置λ。计算中，在每种情况下随机产生10 000条模拟径迹，使用改进爬山法得到每条径迹的拟合参数，表1列出了在不同情况下改进爬山法给出的圆径迹参数的拟合结果及其精度。由计算结果易知，在不同的噪声水平和测量精度下，改进爬山法均能给出较高精度的圆径迹参数拟合值。但随测量不精确度和噪声水平的增加，参数的拟合精度在下降。

图1 测量点及其空间映射Fig.1 Original data points and their transformations in parameters'space

图2 改进爬山法对单圆径迹拟合结果Fig.2 Fitting results of single circle track based on modified mountain method

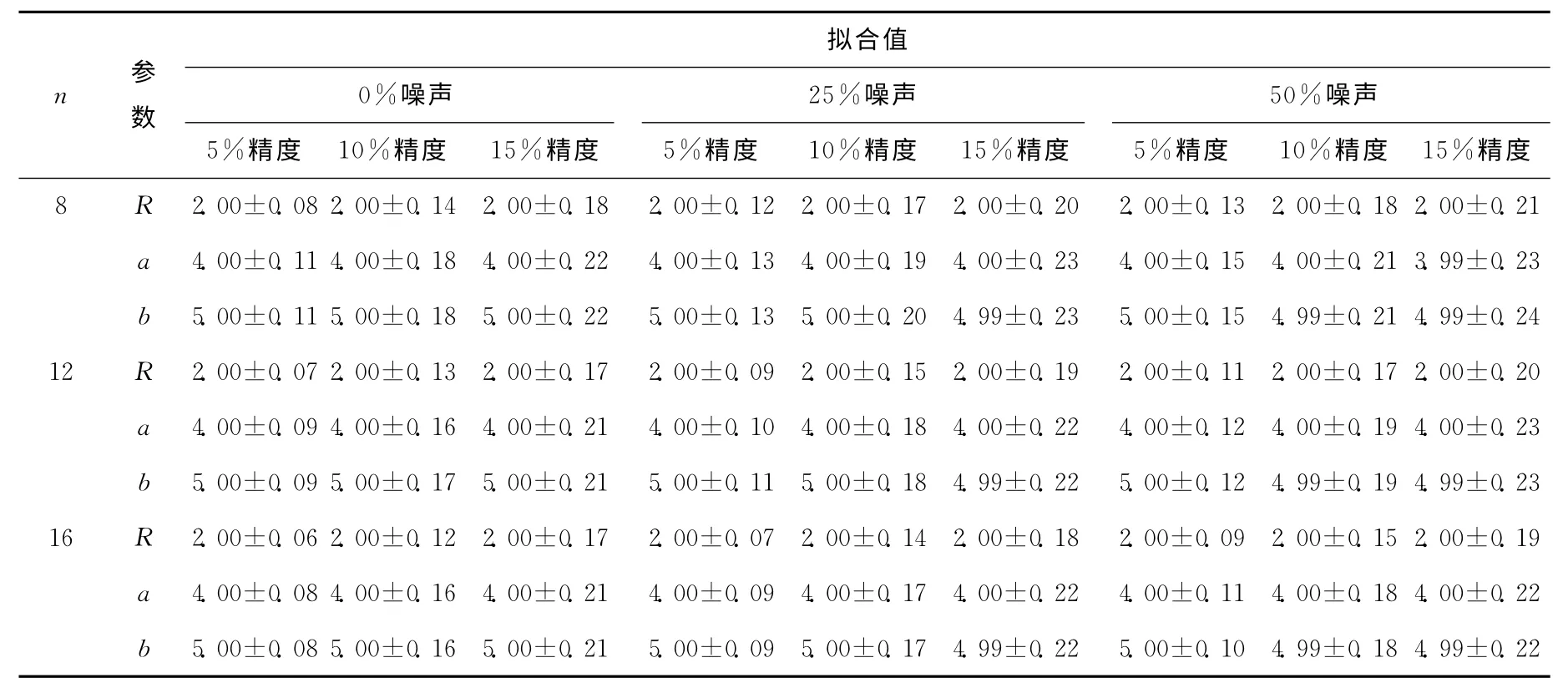
表1 不同情况下改进爬山法对圆径迹参数拟合精度Table 1 Fitting values and their errors derived by modified mountain method under various scenarios

2.2 其他圆径迹重建

图3为高能物理实验中带电粒子在TPC中的投影径迹，TPC 的中心为中心束流管。高能粒子在束流管中的对撞中心点发生碰撞，产生的初级带电粒子的径迹在读出平面上的投影为1段圆弧，该圆弧通过坐标原点，其所对应的圆心角由粒子的动量和磁场强度决定；而对于次级带电粒子的径迹，其圆弧型径迹并不一定通过坐标原点，对应的圆心角同样由粒子的动量和磁场强度决定。

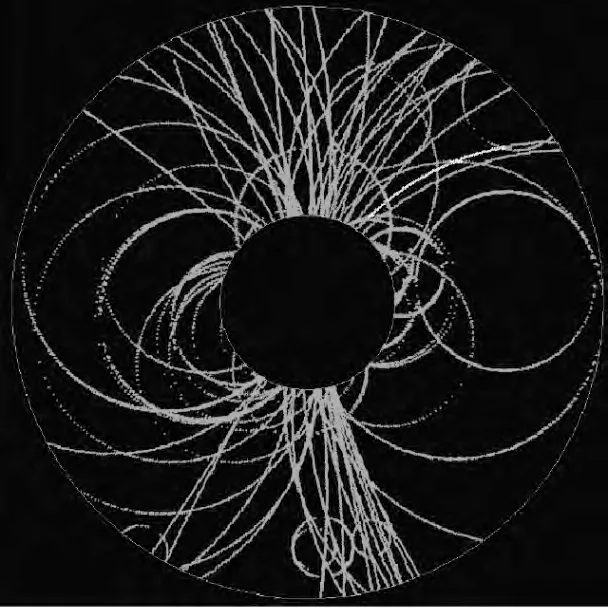
图3 带电粒子在TPC中的投影径迹Fig.3 Track projection of particles'trajectories in TPC

针对几种不同的圆弧型径迹，图4示出了使用改进爬山法的重建结果。图4a～c为单圆弧型径迹的重建结果，图4a为过原点的初级带电粒子产生的圆弧型径迹，该径迹完全投影到了读出平面，图4b为仅部分径迹投影到TPC读出平面的情况，而图4c则为次级粒子产生的径迹情况。图4d～f为上述几种情况下的双圆径迹组合情况下的径迹重建结果。与单圆径迹重建相同，计算中使用参数λρ＝50，噪声点数取信号点数的50%～100%，位置测量的随机误差为径迹半径R 的5%，每条径迹上信号点数在16～21之间。计算结果显示，改进爬山法同样适用于多条圆径迹的重建。

3 结语

本文通过空间映射将二维平面上的带电粒子圆径迹重建问题转变为参数空间上的聚类问题，其中参数聚类中心在参数空间上的位置代表了圆径迹的参数，使用改进爬山法在参数空间上寻找该聚类中心。充分考虑探测器的位置测量不精确度、噪声水平和测量点数等因素，在不同情况下使用改进爬山法计算得到了圆径迹参数的拟合值及其精度。计算结果显示，该方法具有较强的鲁棒性和抗噪声干扰能力，在不同噪声水平下均能给出较高的拟合精度。此外，使用改进爬山法对二维平面上的两条圆径迹进行了重建，结果显示该算法同样适用多条圆径迹的重建。

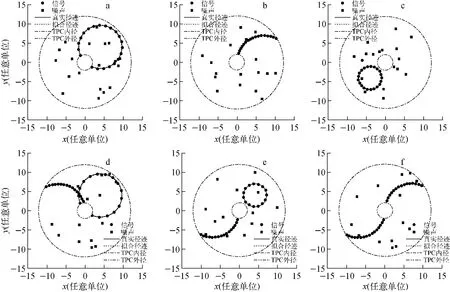
图4 不同类型的圆径迹重建Fig.4 Track reconstruction of circles under various scenarios

［1］ HILKE H J.Time projection chambers［J］.Reports on Progress in Physics，2010，73（11）：116201-116236.

［2］ BOWDEN N S，HEFFNER M，CAROSI G，et al.Directional fast neutron detection using a time projection chamber［J］.Nuclear Instruments and Methods in Physics Research A，2010，624（1）：153-161.

［3］ HANG M，LI Y L，DENG Z，et al.A fast neutron spectrometer based on GEM-TPC［C］∥IEEE Nuclear Science Symposium and Medical Imaging Conference Record （NSS／MIC）.［S.l.］：［s.n.］，2012：146-148.

［4］ FABBIETTI L，ANGERER H，ARORA R，et al.The PANDA GEM-based TPC prototype［J］.Nuclear Instruments and Methods in Physics Research A，2011，628（1）：204-208.

［5］ CHESHKOV C.Fast Hough-transform track reconstruction for the ALICE TPC［J］.Nuclear Instruments and Methods in Physics Research A，2006，566（1）：35-39.

［6］ STRANDLIE A，FRUHWIRTH R.Track and vertex reconstruction：From classical to adaptive methods［J］.Reviews of Modern Physics，2010，82（2）：1 419-1 458.

［7］ TSUJI S，MATSUMOTO F.Detection of ellipses by a modified Hough transformation［J］.IEEE Transactions on Computers，1978，27（8）：777-781.

［8］ YAGER R R，FILEV D P.Approximate clustering via the mountain method［J］.IEEE Transactions on System，Man and Cybernetics，1994，24（8）：1 279-1 284

［9］ YAGER R R，FILEV D P.Generation of fuzzy rules by mountain clustering［J］.Journal of Intelligent and Fuzzy Systems，1994，2（3）：209-219.

［10］CHUI S L.Fuzzy model identification based on cluster estimation［J］.Journal of Intelligent and Fuzzy Systems，1994，2（3）：267-278.

［11］YANG M S，WU K L.A modified mountain clustering algorithm［J］.Pattern Analysis and Applications，2005，8（1）：125-138.