基于时间序列模型的河南省房地产价格研究

聂淑媛， 武新乾

(1．洛阳师范学院数学科学学院 河南 洛阳471022;2．河南科技大学数学与统计学院 河南洛阳471023)

0 引言

近年来房价的持续走高和暴涨势头已引起社会各界的高度关注，国内外学者运用不同方法分析研究房地产市场的发展规律，Malpezzi利用时间序列截面回归分析美国重复交易住宅价格指数［1］;Anglin创建VAR模型预测多伦多的房价变动［2］;Zhou等利用滑动平均预测拉斯维加斯的房价指数［3］;Clapp等根据自回归时间序列模型探究弗洛里达的季度房价［4］;李万庆等借助小波神经网络研究房地产价格指数［5］;闫妍等以TEI@I方法论为指导预测房价变动［6］;王聪［7］和葛龙［8］分别利用多因素logistic回归模型和GARCH模型、COPULA模型研究房地产市场的发展;更有殷霄雯和武秀丽等探讨了南昌、广州等地方性房价．但目前鲜有文献对河南省的房地产价格进行系统研究，本文以时间序列模型为理论基础，以SAS软件为基本工具，对郑州、洛阳和平顶山等代表性城市房地产相关数据进行定量分析，通过纵向和横向的比较，整体和局部的比较，系统概述和适度预测河南省房地产市场的总体态势和运行状况，以期为政府部门、房地产界、普通民众和投资者提供一定的理论参考．

1 样本选取和数据来源

1．1 样本选取

作为河南省省会，郑州也是全国区域性中心城市和金融中心，是河南省“中原城市群”的群中心;作为省内第二大城市和中西部区域的物流枢纽，洛阳是副中心;开封、平顶山和新乡等城市是中原城市群的核心区域，故本文选取郑州、洛阳和平顶山分别作为河南省一线、二线和三线城市的代表．

1．2 指标和数据的选取

鉴于房地产市场动态变化的瞬时性和复杂性，本文选取关注率最高的新建住宅价格指数为指标，样本区间为2009年3月～2013年3月，由于原始数据是以上个月价格为基数的环比序列，数据整体之间不具备可比性，因此把原序列转化为以2009年2月为基数的指数数据．同时，由于住宅价格和住宅商品房的销售面积密切相关，兼顾到数据的易得性，本文选取2006～2012年3地住宅商品房销售面积的年度数据为第二指标，以综合分析房地产市场的供需关系［9－10］．

1．3 数据来源

为确保数据统计口径的一致性和数据的可靠性，本文全部数据来源于国家统计局、河南省统计局、郑州统计局、洛阳统计局和平顶山统计局的统计数据库．其中，2012年的住宅商品房销售面积数据来源于3个城市的年度政府公报，限于篇幅，文章略去了原始数据值．

2 城市住宅价格指数序列实证分析

利用SAS软件，生成3个城市新建住宅价格指数序列的时序图，如图1，3个序列都蕴含着显著的递增趋势，异方差检验显示都具有显著的异方差自相关性，故可对序列拟合求和自回归移动平均ARIMA模型、残差自回归模型或自回归条件异方差GARCH模型［11］．

2．1 对郑州新建住宅价格指数序列的模型创建

2．1．1 拟合ARIMA模型

对郑州新建住宅价格指数zz序列的一阶差分序列dif(zz)，进行ADF单位根检验和纯随机性检验，显示其为平稳非白噪声序列，通过identify命令［12］，生成dif(zz)序列的自相关图和偏自相关图，如图2，自相关函数呈负指数衰减且明显具有拖尾性，偏相关函数一阶截尾，结合AIC和SBC准则，对dif(zz)序列拟合AR(1)模型，利用最小二乘法对参数进行估计，最终得到zz序列的ARIMA(1，1，0)模型，

其中，B为延迟算子，AIC=66．12，SBC=69．86．残差白噪声检验和参数显著性检验显示拟合模型显著有效．

图1 3个城市新建住宅价格指数序列时序图Fig．1 The newly built housing price index series figure of three cities

图2 dif(zz)序列的自相关图和偏自相关图Fig．2 The autocorrelation and partial autocorrelation figure of dif(zz)series

2．1．2 拟合以时间变量t为因子的残差自回归模型

图1显示zz序列有显著的递增趋势，但没有季节效应，故可拟合残差自回归模型:

假设趋势效应TRt以时间变量t为自变量，可建立线性模型zzt=a+bt+εt，通过Autoreg程序，可得残差序列{εt}DW检验的统计量值为0．06，其相伴概率P值小于0．000 1，{εt}序列显著正相关．为拟合{εt}的自相关模型，在Autoreg程序中添加逐步回归选项backstep，以筛选出显著的自相关因子，使用极大似然法进行参数估计，zz序列拟合模型的输出信息如图3，模型结构为

其中，AIC=70．34，SBC=77．91，可决系数 R2=0．994 9．

2．1．3 拟合以延迟因变量zzt－1为因子的残差自回归模型

若假设 TRt以延迟因变量 zzt－1为自变量，创建回归模型 zzt=a+bzzt－1+ εt［13］，可得{εt}Durbinh 统计量值为4．12，相伴概率P值为0．000 1，残差序列显著正相关．由于常数项a不显著(P值大于0．39，远远大于显著性水平0．05)，为充分提取相关信息，增加noint选项除去常数项，对{εt}序列再次拟合，可得zz序列最终拟合模型的输出信息，如图4，则拟合模型为

其中，AIC=66．43，SBC=70．17，R2=1．

图3 zz序列关于时间变量t的回归分析结果Fig．3 The regression analysis result of zz series about time variable

图4 zz序列带延迟因变量回归分析结果Fig．4 The regression analysis result of zz series about lag variable

2．1．4 拟合GARCH模型

对zz序列拟合残差自回归模型后，PQ检验和LM检验显示残差序列具有显著的异方差性，自相关图显示残差序列具有显著的长期自相关性，综合考虑检验结果，经反复尝试，最终确定拟合无回归常数项的AR(3)-ARCH(1)模型，输出结果如图5，模型口径为

其中，AIC=57．80，SBC=67．16，R2=1．检验结果显示除ARCH(1)模型中的常数项不显著外，其他变量均显著，且正态性检验的概率P值0．66远大于0．05，与假定GARCH模型残差项服从正态分布相吻合，原始数据和拟合值的对比效果图如图6，图中的两条曲线几乎重合，模型拟合效果满意．再综合对比AIC、SBC值和可决系数R2，确定郑州新建住宅价格指数序列最优拟合模型是AR(3)-ARCH(1)模型．

2．2 对洛阳和平顶山新建住宅价格指数序列的模型创建

因洛阳新建住宅价格指数ly序列、平顶山新建住宅价格指数pds序列和zz序列具有较相似的递增趋势，故对此序列同样进行上述4类模型的拟合比较，具体分析过程略，得ly序列的最优拟合模型为

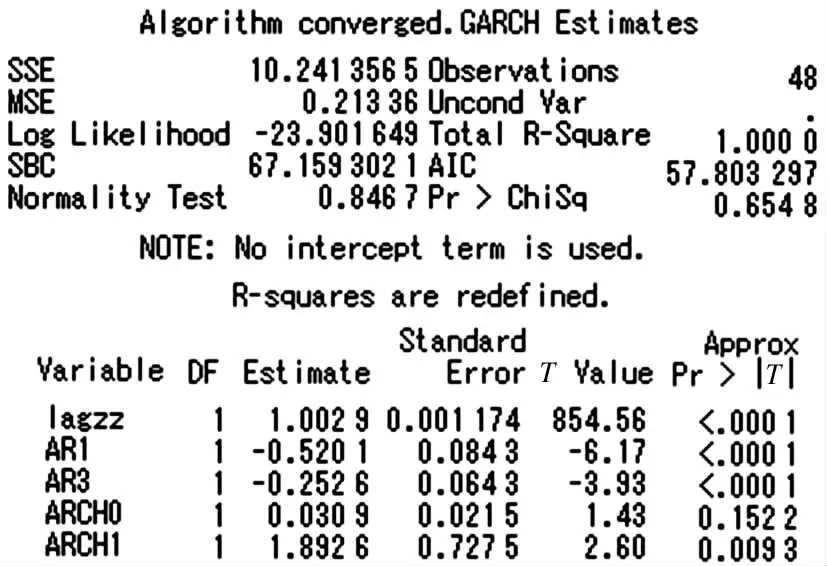
图5 zz序列拟合GARCH模型输出结果Fig．5 The GARCH estimate result of zz series

图6zz序列拟合AR(3)-GARCH模型效果Fig．6 Comparison of zz series fitting AR(3)-GARCH model

其中，AIC=84．82，SBC=92．39，R2=0．987 4．pds序列的最优拟合模型为

其中，AIC=72．62，SBC=80．19，R2=0．979 5．

3 结论

尽管3个城市的房价指数都近似线性递增，但实证分析表明郑州住宅价格指数的波动程度和异方差性最显著，其平均增长幅度约为0．7% ～1．1%，2010年10月、2011年2月和2013年1～3月等特定时间段内高达1．8% ～2．1%，远远高于洛阳的0．4% ～0．6%和平顶山的0．2% ～0．3%．而根据预测结果(表1)，郑州的上涨幅度依然维持在1．4% ～1．5%，洛阳和平顶山则分别约为0．5%和0．3%．同时，由住宅商品房销售面积的时序图图7可知，郑州近3年的商品房销售面积分别为1 085．14万 m2、1 428．61 万 m2和1 306．38 万 m3，几乎是同时期内洛阳销售面积(356．91 万 m2、405．37 万 m2和 512．09 万 m2)的3倍，是平顶山的十几倍．究其原因，郑州作为河南省的政治、经济、金融、科研和文化中心，现代大都市的魅力逐渐吸引了省内外更多的关注目光，土地的稀缺，大量外来人口的涌入使住宅商品房处于高需求状态，房价一路飞涨．相比之下，无论是商品房的销售量还是住宅价格，洛阳和平顶山的增幅都相对平缓、稳定，故这两个城市的住宅价格指数序列在异方差GARCH模型拟合中未能取得理想效果，与郑州截然不同．

表1 3个城市新建住宅价格定基指数预测(2013年4月～9月)Tab．1 The forecast indices about the newly built housing price of three cities from April to September in 2013

图7 3个城市住宅商品房销售面积时序图Fig．7 The sale area series figure of commercial house of three cities

就洛阳和平顶山而言，虽然2者的拟合模型极其相似，但差距不容忽视，尤其是2011年4月～2012年末，其住宅价格指数的差距值基本上保持在4．7～4．9个点，2011年9月和10月的差距甚至达到5个点，而同时期洛阳与郑州住宅价格指数的差距值则维持在3．6～3．9个点，2012年上半年一度缩小到2．7个点，洛阳与平顶山的差距超越了洛阳与郑州的差距，这也印证了洛阳作为河南省第二大城市的定位．从图7可清晰看到，当2010年和2011年郑州商品房的销量急剧下滑时，洛阳的销量却呈现上升态势或缓慢的下降，事实上，由于一线城市高昂的房价和生活成本的突增，不少人退而求其次，开始选择二线城市，故洛阳的房地产市场有着巨大的潜在性需求，这一因素客观上必将刺激其住宅价格的上涨．平顶山的房价和销售量始终是稳中有升，受国内外经济环境的影响反而比一线和二线城市要小得多．

总体来看，河南省的房价近期仍处于上升态势，一线城市波动最大，二线城市次之，三线城市最小，它们之间的差距逐渐加大．基于此，建议政府有关部门在宏观调控房地产市场时，应该采取有区别的针对性措施，抑制一线城市的过度波动，打压房地产泡沫现象，引导二线城市的健康发展，巩固三线城市的稳步态势．

［1］ Malpezzi S．A simple error correction model of housing prices［J］．Journal of Housing Economics，1999，8(1):27 －62．

［2］ Anglin P．Local dynamics and contagion in real estate markets［C］//The International Conference on Real Estates and Macro E-conomy．Beijing，2006:19 －24．

［3］ Zhou W X，Sornette D．Analysis of the real estate market in Las Vegas:bubble，seasonal patterns，and prediction of the CSW indices［J］．Physica A:Statistical Mechanics and its Applications，2008，387(1):243 － 260．

［4］ Clapp J M，Giaccotto C．Evaluating house price forecasts［J］．Journal of Real Estate Research，2002，24(1):1 －26．

［5］ 李万庆，张金水，孟文清．基于小波神经网络的房地产价格指数预测研究［J］．河北工程大学学报:自然科学版，2008，25(1):74－76．

［6］ 闫妍，许伟，部慧，等．基于TEI@I方法论的房价预测方法［J］．系统工程理论与实践，2007，27(7):1－9．

［7］ 王聪．基于多因素logistic的城市房地产价格模型研究［D］．大连:大连理工大学，2008．

［8］ 葛龙．基于GARCH和COPULA模型的天津房地产市场预测［D］．天津:天津大学，2008．

［9］ 国家统计局．中国统计年鉴［M］．北京:中国统计出版社，2013:102－420．

［10］河南省统计局．河南统计年鉴［M］．北京:中国统计出版社，2013:220－315．

［11］梁保松，陈振，党耀国．具有灰指数律数据序列建模方法研究［J］．郑州大学学报:理学版，2007，39(1):116－118．

［12］王燕．应用时间序列分析［M］．北京:中国人民大学出版社，2008:180－240．

［13］李正辉，李庭辉．时间序列分析实验［M］．北京:中国统计出版社，2010:58－79．