微小型无人直升机避障最优轨迹规划
孟少华 向锦武 罗漳平 任毅如
(北京航空航天大学 航空科学与工程学院,北京 100191)
无人机在国土防御和经济建设领域得到了越来越广泛的应用,无人直升机更因其独特的垂直起降和空中悬停性能而倍受青睐.在复杂、受限的空间中,无人直升机可以利用其悬停、横飞、倒飞等飞行方式穿梭于障碍物之间,完成战场侦查、地形测量、抢险救灾等任务.与地面车辆不同的是,任何碰撞对于无人直升机都是致命的,直接导致预定任务失败,自主避险能力是其顺利完成任务的关键所在.
轨迹规划技术作为无人直升机自主飞行研究的重要内容,受到了国内外学者的广泛关注.现有的路图法(roadmap)、人工势场法(artificial potential field)、单元分解法(cell decomposition)等方法仅能够得出安全的飞行路径,并不能考虑飞行器自身的动力学特性,属于路径规划方法,研究内容主要侧重于算法的有效性和鲁棒性,无法保证路径是真实可行的.区别于路径规划,轨迹规划不仅要寻找一条从起点到终点的最优无碰撞路径,同时还要给出相应的状态量和控制输入量,被广泛应用于机器人、无人车辆和无人飞行器等各种操纵平台上[1-4].
目前,针对轨迹规划的研究大都采用最优控制法,应用领域也主要局限在动力学方程较为简单的地面无人车辆.文献[5]建立了地面车辆的三自由度动力学方程,采用最优控制法研究了二维平面内的轨迹规划.而目前对于无人直升机轨迹规划的研究较少,文献[6]将无人直升机的三维运动简化为质点运动模型,以加速度为伪控制输入量,得出避障机动的最优轨迹.由于在此过程中并没有考虑直升机复杂的动力学特性,也就无法保证轨迹是真实可飞的.因此有必要开展考虑无人直升机动力学特性的轨迹规划方法的研究.
本文以某无人直升机为例研究了避障最优轨迹规划问题.以最短避障时间为目标,考虑了无人直升机六自由度动力学方程以及飞行性能为约束,利用绝对值性质将三维空间障碍物的限制转化为不等式约束,建立了无人直升机避障飞行的最优控制模型,利用高斯伪谱法对其进行求解.为无人直升机在低空、复杂、受限空间内的避障飞行提供了全局轨迹规划方法.
1 避障最优轨迹规划建模
1.1 无人直升机飞行动力学模型
本文采用无人直升机六自由度刚体运动方程,向量[x,y,z,φ,θ,ψ]T表示直升机在惯性坐标系下的位置和欧拉角,其运动学方程为
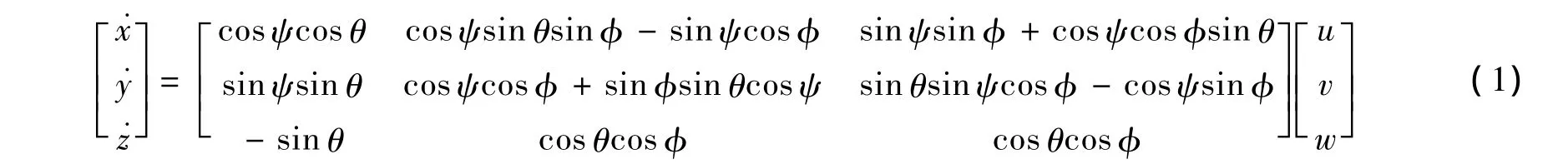

式中,[u,v,w]T为体轴坐标系下的直升机线速度矢量;[p,q,r]T为角速度矢量.
无人直升机体轴坐标系下的飞行动力学微分方程如下:

式中,m为全机质量;Ixx,Iyy,Izz为机体3个轴方向的惯性矩;下标 mr,fus,tr,vf,ht分别表示主旋翼、机身、尾桨、垂直和水平安定面;X(·),Y(·),Z(·)和 L(·),M(·),N(·)表示直升机各部件产生的力和力矩在体轴系下的投影(图1),其中主旋翼和尾桨产生的力和力矩是控制量 ucon= [δcol,δlon,δlat,δped]T的函数,具体表达式参见文献[7 -8].

图1 无人直升机体轴系及受力示意图
为了考虑操纵系统对控制速率的限制,同时也为了避免控制输入量出现跳跃或“bang-bang”型控制,使用操纵量的一阶导数代替操纵量作为控制输入,而将操纵量视为状态变量,实现对状态方程的扩维.
最后可写作非线性微分方程的标准形式:

1.2 障碍物约束模型
当前障碍物建模大都采用p-norm方法[9],对于球形或圆柱形障碍物可以取p=2.然而对于长方体形状的障碍物,p只有取较大值时才能得到较为满意的近似结果,同时会导致计算量过大,对于复杂动力学方程问题极有可能不收敛.因此针对长方体形状的障碍物,本文构建了一种基于绝对值的约束方式.
假设障碍物在全局坐标系下占据的空间位置为[X1,X2],[Y1,Y2],[Z1,Z2],则障碍物的尺寸为 ΔX=X2-X1,ΔY=Y2-Y1,ΔZ=Z2-Z1.
假设(x,y,z)为空间任意一点,构建标量:

式中

如果C<0,当且仅当XX <0,YY<0,ZZ <0时成立,即 x∈[X1,X2],y∈[Y1,Y2],z∈[Z1,Z2],表明点(x,y,z)位于障碍物内部,否则位于外部.
1.3 非线性最优控制模型
无人直升机避障机动飞行的最优控制问题可以表述为:在满足直升机自身性能和避障安全约束的条件下,寻找控制输入量,使直升机飞行时间最短.为了使控制输入较为平滑,选择控制输入的一阶导数加权作为目标函数的一部分,具体形式如下:

式中 ωi(i=1,2,3,4)为权重系数.同时状态变量和控制变量满足动力学微分方程(9)以及障碍物引起的路径约束:

式中M为障碍物的个数.
2 求解方法
高斯伪谱法(GPM,Gauss Pseudospectral Method)是近些年来发展起来的一种直接法[10],该方法利用全局插值多项式在一系列的配点上近似状态量和控制量,相比于其他的直接配点法,具有能够以较少的节点获得较高精度的优点.此外GPM离散化得到的NLP(Non-Linear Programming)问题的 KKT(Karush-Kuhn-Tucher)条件与离散的哈密尔顿边值问题一阶最优性条件是等价的[11],能够保证解的最优性.
本文采用高斯伪谱法将连续无穷维的最优控制问题转化为离散有限维的NLP问题,然后利用SQP(Sequential Quadratic Programming)法对其进行求解,具体过程如下:
1)时域变换.
由于高斯伪谱法的配点分布在区间[-1,1]上,需要将初始优化问题的时间区间由t∈[t0,tf]转换到τ∈[-1,1],故对时间变量t做如下映射变换:

2)微分方程约束转化为代数约束.
高斯伪谱法需要在一系列的离散点上对状态变量和控制变量进行全局插值多项式逼近,选择包括初始点t0,N个LG(Legendre-Gauss)点及终止点tf在内的N+2个配点对连续的状态变量和控制变量进行离散化插值逼近:
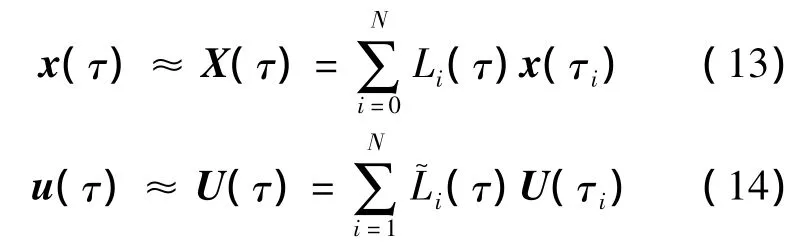
式中Lagrange插值基函数:
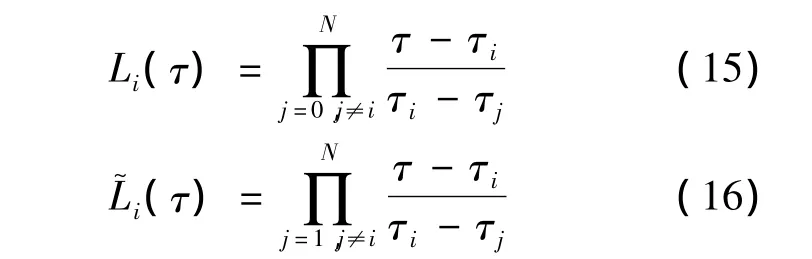
式中 τi(i=1,2,…,N)为 LG 点.
对式(13)进行求导,可得

式中微分矩阵D∈RN×(N+1)的表达式为
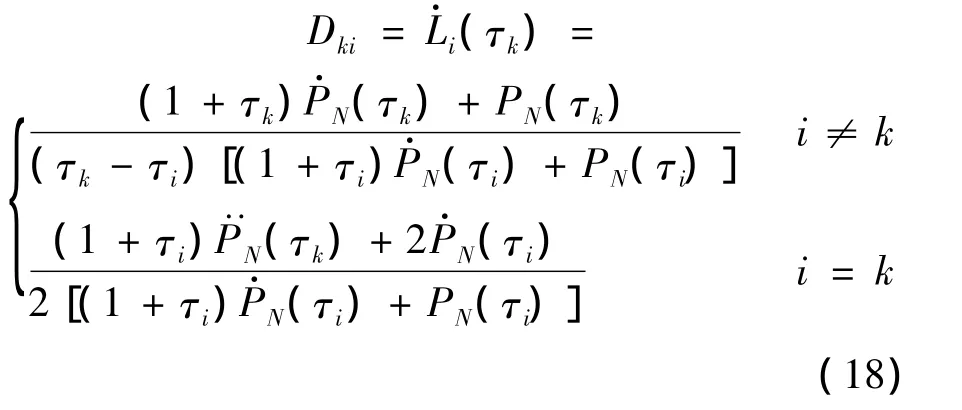
式中,PN为N阶Legendre多项式;i=0,1,…,N.
将式(13)、式(14)及式(17)代入到式(9),可将动力学微分方程约束转换为代数约束,即
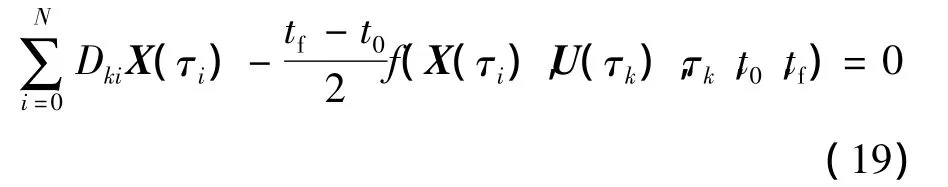
式中 k=1,2,…,N.
3)终端状态约束的离散化.
虽然高斯伪谱法中的配点包括了终端点τf≡1,但式(13)中并未定义终端状态Xf.由于终端状态满足动力学方程约束,为此需要用Gauss积分来近似,可得


4)离散条件下的性能指标.
将性能指标函数中的积分项用Gauss积分来近似,可得离散条件下的性能指标函数:

采用上述方法,利用高斯伪谱法将连续最优控制问题离散化,转化为NLP问题:以状态变量(X0,X1,…,XN)、控制变量(U1,U2,…,UN)、初始时刻t0和终端时刻tf(如果t0和tf未知)作为决策变量,使性能指标最小,并满足配点处状态约束,终端约束以及边界条件

和路径约束

式中 k=1,2,…,N.
最后得到的NLP问题可以采用序列二次规划算法进行求解[12].该算法收敛性好、计算效率高,可以有效处理约束条件.
3 数值结果
无人直升机的结构参数见文献[7],飞行性能约束可以转化为对状态变量和控制变量的参数约束,如表1所示.

表1 模型直升机状态量和控制量边界
3.1 三维空间避障机动飞行仿真
为了验证该方法的有效性,在虚拟的包含多个障碍物的三维空间进行仿真,障碍物位置参数如表2所示.

表2 障碍物位置参数 m
初始时刻直升机在点A(0,0,10)稳定悬停,目标点B的坐标为(95,0,10),终端状态量亦为悬停,目标函数选择为飞行时间.考虑到时间最优所产生的飞行轨迹必然会紧贴着障碍物,而直升机是有尺寸的,所以对障碍物模型进行放大,以保证所得轨迹切实可行,此处选择最小安全距离为飞行器尺寸的2倍.
仿真试验采用无障碍物飞行轨迹为初始猜测值,设置了80个插值点,求得的最短飞行时间为12.7481 s,计算耗时 3 s左右.
图2给出了最优轨迹的三维视图.从中可以看出,生成的机动飞行轨迹较为平滑,而且灵巧地避开障碍物威胁.

图2 无人直升机最优避障轨迹三维视图
图3~图6给出了状态量随时间的变化曲线.从中可以看出,计算结果均满足表1中所设定的性能约束条件.直升机从悬停状态开始加速飞行,在左转躲避障碍物1的同时拉升高度躲避障碍物2,为了保持飞行时间最短,前飞速度大约从4.2~8.2 s一直保持最大.飞跃障碍物2后,直升机开始减速并右转躲避障碍物3,最后安全抵达目标点.在整个避障飞行过程中,滚转角先增大后减小,俯仰角和偏航角先减小后增大,且关于飞行时间的一半近似对称,主要是由于仿真场景近似对称.
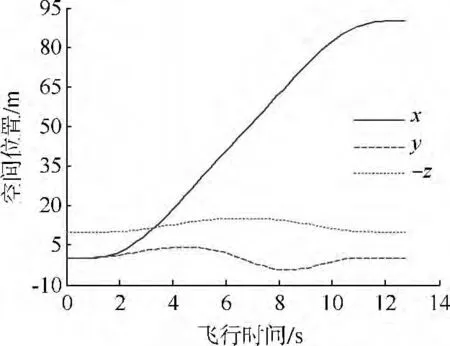
图3 空间位置随时间的变化曲线
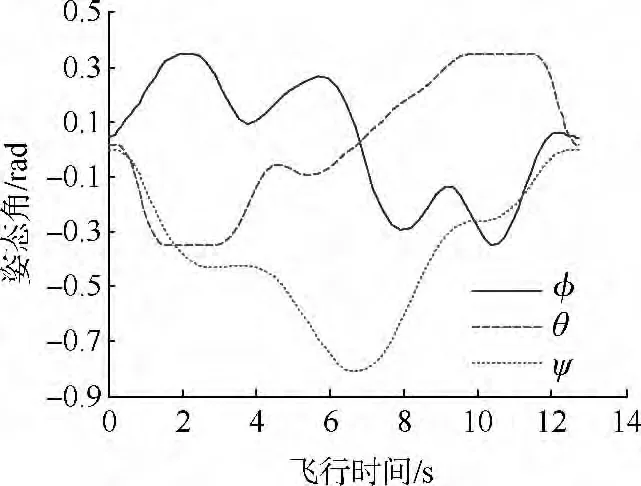
图4 姿态角随时间的变化曲线
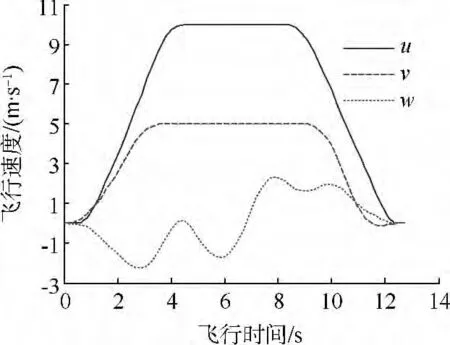
图5 飞行速度随时间的变化曲线

图6 角速度随时间的变化曲线
图7给出了操纵输入随时间的变化曲线,可以看出均满足操纵边界限制,同时也无出现操纵量急剧变化的情况.

图7 最优轨迹的控制量变化曲线
3.2 避障机动分叉点及分析
考虑到SQP算法为一种局部寻优求解策略,障碍物形状和尺寸对最优轨迹有一定的影响.如图8所示,对于最为常见的长方体障碍物,避障机动动作可以选择爬升或转弯,单凭经验无法判断哪种是最优的.鉴于此,本文研究了其纵向尺寸H和横向尺寸L对避障轨迹的影响.如图9所示,爬升机动和转弯机动飞行时间分别随着纵向和横向尺寸增加而增加,纵横尺寸相同时,转弯机动所需时间较小.通过插值处理即可得到在相同飞行时间下爬升机动和转弯机动所对应的障碍物纵向和横向尺寸,如图10所示.二者关系近似为一条斜率为0.5的直线.当障碍物的纵横尺寸落在左上区域时,转弯机动为最优机动动作;反之,爬升机动为最优机动动作.

图8 多种避障机动示意图
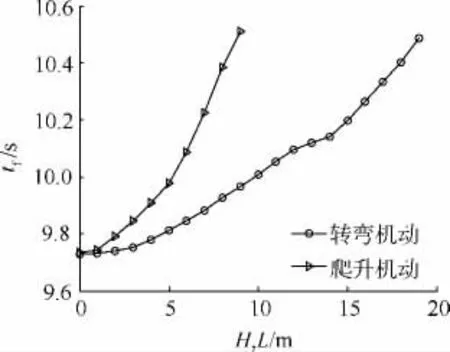
图9 飞行时间随障碍物尺寸的变化曲线
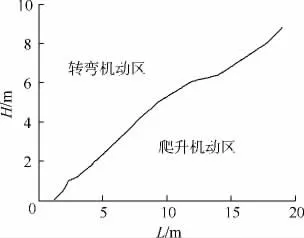
图10 避障机动动作与障碍物尺寸的关系
4 结论
本文研究了复杂低空环境下无人直升机避障最优轨迹规划问题.建立了直升机避障机动飞行的非线性最优控制模型.与传统的轨迹规划方法相比,该模型考虑了复杂的直升机动力学方程及其自身的飞行性能限制等因素,利用绝对值的性质将三维障碍物的空间限制转化为不等式约束.仿真结果表明,该方法能够以较高的精度生成可行的飞行轨迹,可以为无人直升机自主飞行提供全局最优轨迹.此外,针对最为常见的长方体障碍物研究了其尺寸对最优轨迹的影响.当长方体的纵横尺寸比约小于1∶2时,垂直爬升为最优避障机动;反之,水平转弯为最优.
References)
[1] Pettersson P O,Doherty P.Probabilistic roadmap based path planning for an autonomous unmanned helicopter[J].Journal of Intelligent and Fuzzy Systems,2006,17(4):395 -405
[2]于振中,闫继宏,赵杰,等.改进人工势场法的移动机器人路径规划[J].哈尔滨工业大学学报,2011,43(1):50 -55 Yu Zhenzhong,Yan Jihong,Zhao Jie,et.al.Mobile robot path planning based on improved artificial potential field method[J].Journal of Harbin Institute of Technology,2011,43(1):50 - 55(in Chinese)
[3] Tsenkov P,Howlett JK,Whalley M,et al.A system for3D autonomous rotorcraft navigation in urban environments[R].AIAA 2008-7412,2008
[4]梁宵,王宏伦,李大伟,等.基于流水避石原理的无人机三维航路规划方法[J].航空学报,2013,34(7):1670 -1681 Liang Xiao,Wang Honglun,Li Dawei,et al.Three-dimensional path planning for unmanned aerial vehicles based on principles of stream avoiding obstacles[J].Acta Aeronautica et Astronautica Sinica,2013,34(7):1670 -1681(in Chinese)
[5] Hurni M A,Sekhavat P,Ross IM.Autonomous path planning using real-time information updates[R].AIAA 2008-6305,2008
[6] Moon J,Prasad JV R.Minimum-time approach to obstacle avoidance constrained by envelope protection for autonomous UAVs[J].Mechatronics,2011,21(5):861 -875
[7] Koo T J,Sastry S.Output tacking control design of a helicopter model based on approximate linearization[C]//Proceedings of the 37th IEEE Conference on Decision & Control.Tampa:IEEE,1998:3635-3640
[8] Gavrilets V,Mettler B,Feron E.Nonlinear model for a small-size acrobatic helicopter[R].AIAA 2001-4333,2001
[9] Gatzke B T.Trajectory optimization for helicopter unmanned aerial vehicles[D].Monterey:Naval Postgraduate School,2010
[10]陈功,傅瑜,郭继峰.飞行器轨迹优化方法综述[J].飞行力学,2011,29(4):1 -5 Chen Gong,Fu Yu,Guo Jifeng.Survey of aircraft trajectory optimization methods[J].Flight Dynamics,2011,29(4):1 - 5(in Chinese)
[11] Benson D.A Gauss pseudospectral transcription for optimal control[D].Bostom:Massachusetts Institute of Technology,2004
[12] Gill P E,Murray W,Saunders M A.SNOPT:an SQP algorithm for large-scale constrained optimization [J].Society for Industrial and Applied Mathematics,2005,47(1):99 - 131

