高超声速飞行器异步切换的鲁棒H∞控制

吴振东 王 青

(北京航空航天大学 自动化科学与电气工程学院，北京 100191)

董朝阳

(北京航空航天大学 航空科学与工程学院，北京 100191)

由于高超声速飞行器的飞行包线跨度大，其气动力特性在飞行过程中改变显著，导致动力学特征和模型参数沿飞行轨迹变化非常快，工程上常采用增益调度方法设计此类系统的控制器［1］，但该方法难以保证闭环控制系统的稳定性.为了弥补上述方法的不足，学者将切换系统理论应用于高超声速飞行器的控制器设计中［2－6］，取得了很好的设计效果，这些研究工作均是基于子系统与控制器同步切换.考虑飞行器实际工作中，从辨识工作子系统到激活相应的子控制器需要一定的时间，即控制器切换时刻会滞后于子系统，极易导致高超声速飞行器控制系统切换过程的动态跟踪特性变差，甚至造成闭环系统的不稳定，因而有必要研究飞行器子系统与控制器的异步切换.

近年来对子系统与控制器异步切换研究取得了一些优秀的成果［7－10］.文献［7］分析异步切换对状态和控制受限系统的影响;文献［8］针对切换信号的延迟，设计了异步切换控制器，并分析了闭环系统的稳定性.以上文献均保证了异步切换系统的稳定性，且优化了控制器异步切换的过渡过程，但因采用驻留时间的方法，为子系统工作附加了时间约束，增加了设计的保守性.针对此问题，文献［9－10］采用平均驻留时间方法，设计了离散和连续系统的异步切换控制器，但没有考虑不确定性，难以直接应用于具有不确定性的高超声速飞行器控制系统的分析与设计中.

本文为克服以上研究的局限，针对高超声速飞行器子系统与控制器异步切换，提出了一种鲁棒H∞控制策略.构造了依赖于控制器切换信号的Lyapunov函数，有利于异步切换系统的控制器设计，同时也适用于异步切换导致的闭环子系统不稳定情况.结合平均驻留时间和Lyapunov函数，设计了异步切换的鲁棒H∞控制器.

1 异步切换系统建模

以高超声速飞行器［11］的纵向飞行动态为例，不失一般性，仅考虑飞行器的纵向短周期运动，假定每一个工作点处的纵向短周期线性模型可以表征工作点附近的飞行动态，建立如下带有扰动的不确定线性切换系统:

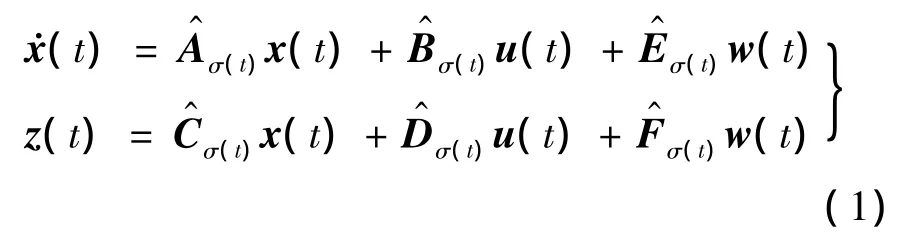
其中，x(t)=［α q］T为系统状态，α，q分别为迎角和俯仰角速率;u(t)=［ξeη］T为控制输入，ξe为升降舵偏转角，η为节流阀调定指令;扰动输入变量w(t)=［w wx］T，w和wx分别为垂向风速及其沿前向的梯度;z(t)为被控输出;σ(t):N→Ω={1，2，…，k}为切换律，表征飞行器工作点随时间变化规律;分别为第 i个工作点的不确定性系数矩阵，其描述如下:

其中，Ai，Bi，Ci，Di，Ei，Fi是标称系数矩阵;Ui1，Ui2，Vi1，Vi2，Vi3是具有适当维数的实常数矩阵，由子系统系数矩阵的不确定项求解可得;Γ是满足ΓTΓ≤I的未知参数矩阵.

飞行器控制系统设计任务是实现控制系统的稳定和对给定指令信号的跟踪控制，考虑飞行器实际工作中，从辨识工作子系统到激活相应的子控制器需要一定的时间τi，如图1所示.

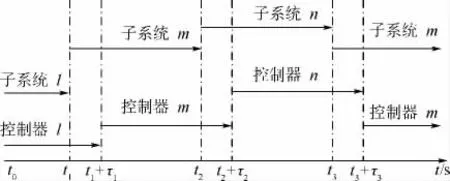
图1 子系统与控制器异步切换示意图

设计如下形式的控制器:

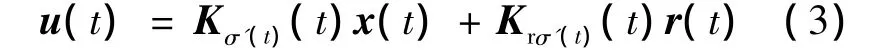
其中，Kσ'(t)，Krσ'(t)(t)分别为控制器中的反馈控制律和前馈控制律;r(t)为给定的指令信号;σ'(t)为控制器的切换律.

假定控制器切换滞后时间τi均不大于常数τd，则 σ'(t)可表示为

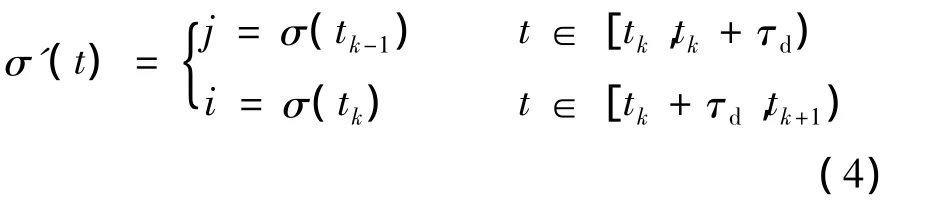
2 控制器设计与分析

定义1［4］对于任意切换信号 σ(t)和任意时刻的 t＞t0，令 Nσ(t)(t0，t)表示 σ(t)在时间间隔(t0，t)的切换次数.如果对于任意给定的 N0，τa＞ 0 ，使得Nσ(t)(t0，t)≤N0+(t－t0)/τa成立，则称τa为平均驻留时间.不失一般性，本文假设N0=0.

针对不确定线性切换系统(式(1))，设计控制器，并找到使得闭环切换系统全局一致渐近稳定且具有H∞性能上界的最小平均驻留时间.

定理1 对于给定常数 α ＞0，β＜α，γ＞0，εi＞0，εij＞0 和 μ ＞1，若存在正定矩阵 Xi，Xj，适维矩阵Wi，Wj，使得如下线性矩阵不等式成立:

其中

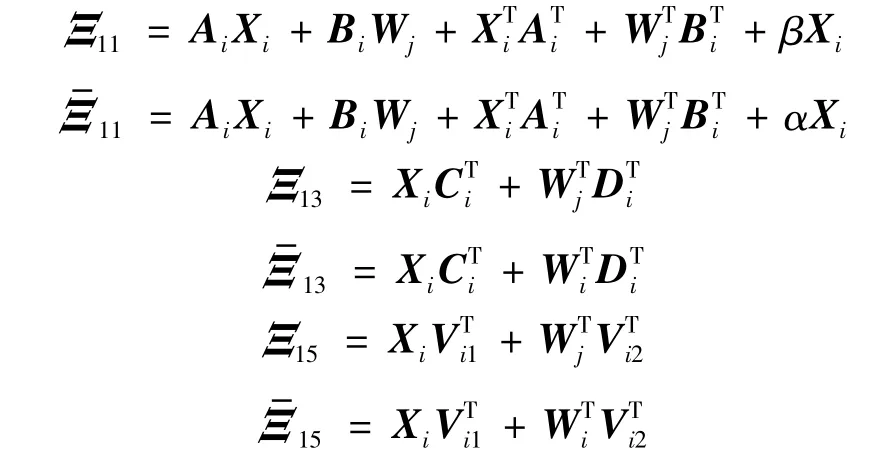
且切换律满足平均驻留时间τa约束:

则控制器(3)中反馈控制器Kσ'(t)(t)选取如下参数:

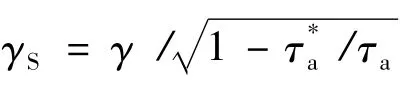
证明 构造准Lyapunov函数V(x)=xTPσ'(t)x ，当 t∈［tk，tk+ τd)时有

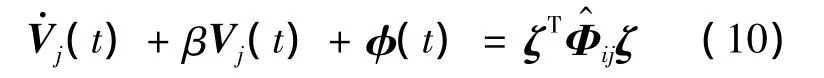
其中

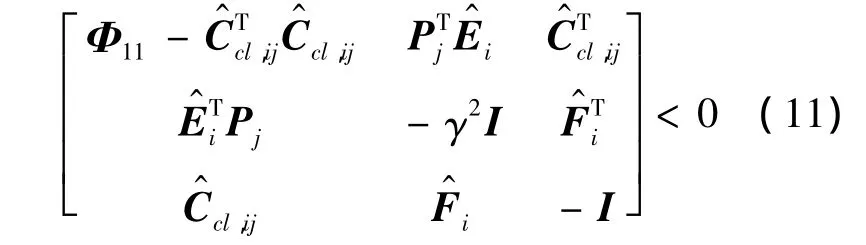
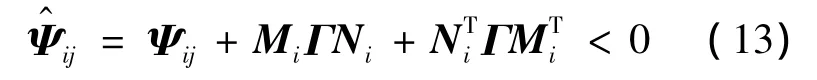
其中

式(13)对所有ΓTΓ≤I成立，当且仅当存在εij＞0，使得如下不等式成立:

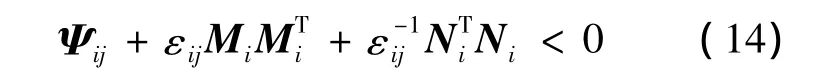
由Schur补引理，式(14)等价于

将 Ψij，Mi和 Ni代入式(15)，并令 Wj=KjXj，即得到式(5).

综上，当 t∈［tk，tk+ τd)时，可得

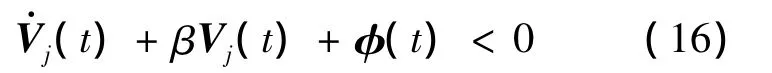
同理，当 t∈［tk+ τd，tk+1)时，由式(6)可得

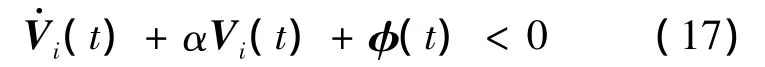
对式(7)应用2次Schur补引理，得

由 V(x)=xTPσ'(t)x ，可得

下面基于式(16)～式(19)，给出系统全局一致渐近稳定和H∞性能上界的证明.

1)全局一致渐近稳定性分析.

令w(t)≡0，由式(16)和式(17)有

令Γa(T1，T2)表示［T1，T2)内控制器处于异步状态的总时长，基于式(19)和式(20)进行如下推导，得

2)H∞性能分析.

基于式(16)、式(17)和式(19)可得

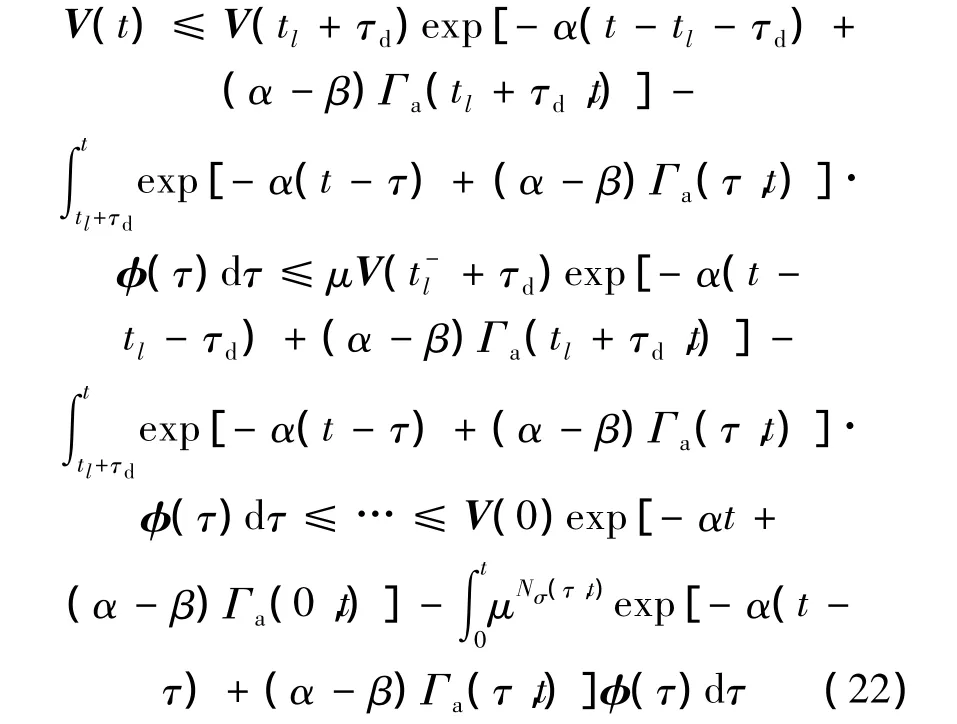
结合平均驻留时间条件式(8)，在零初始条件下，式(22)可得

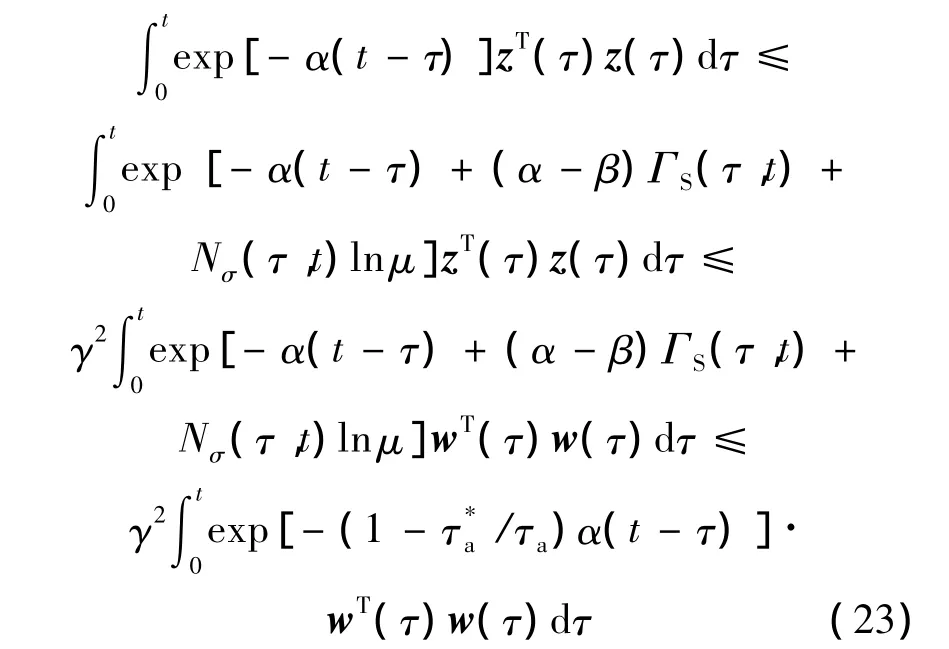
对式(23)两端进行积分，得

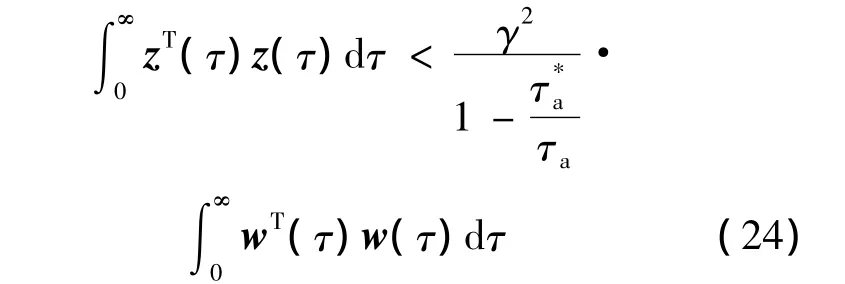
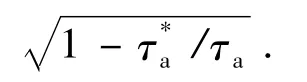
证毕

通过定理1可知，高超声速飞行器子系统与控制器异步切换的稳定性和H∞性能由式(5)～式(8)保证;从V(x)=xTPσ'(t)x和式(20)可知，Lyapunov函数依赖于控制器的切换信号，有利于异步切换系统的控制器设计，同时也适用于异步切换导致的闭环子系统不稳定情况(β＜0)，放宽了激活子系统能量函数是单调递减的条件，降低设计的保守性.

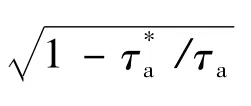
为了使系统的输出z(t)跟踪有界分段连续的参考指令信号r(t)，控制器(式(3))中前馈控制律Krσ'(t)选取如下参数:

其中，l∈σ'(t);C为系统输出矩阵.在系统镇定的情况下，按式(25)设计的前馈控制律Krσ'(t)可以实现对给定指令信号r(t)的无差跟踪［12］.

3 仿真验证

为验证本文方法的有效性，采用文献［11］的高超声速飞行器模型，选择不同区域的工作点进行切换系统分析，工作点的平衡状态见表1.

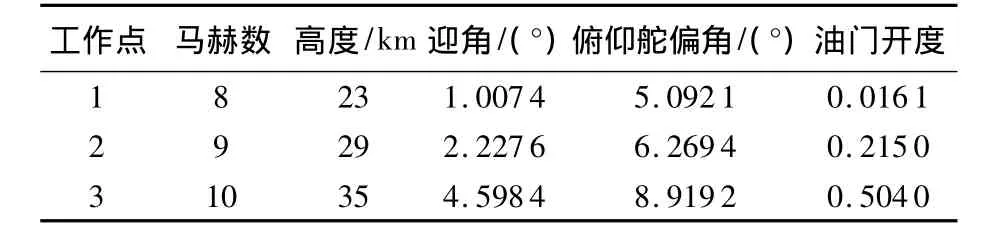
表1 高超声速飞行器工作点的平衡状态

不确定线性切换系统(式(1))中各标称系数矩阵如下:

系统的不确定系数矩阵是由标称系数矩阵加上不确定矩阵，系统的不确定性主要考虑各气动导数，因此在各气动导数上分别加入±15%偏差，获得系统不确定矩阵，按照式(2)进行分解获得Ui1，Vi1，Vi2，Ui2=Vi3=0.选取 α =0.95，β = －0.5，τd=1.5s，γ =32.6，采用Matlab 的YALMIP 工具箱实现定理1，得到μ在10－3误差精度下的极小值和平均驻留时间上界为μ=1.532和，解得切换系统反馈控制器Kσ'(t)如下:

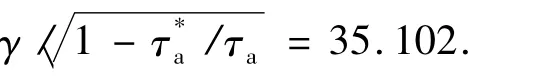
图2 飞行轨迹的马赫数和高度变化曲线

图3 子系统与控制器异步切换信号曲线

考虑在无外部干扰的条件下，子系统与控制器异步切换的响应曲线如图4和图5所示.仿真结果表明:飞行器对指令的跟踪时间短，跟踪精度高，具有良好的动态响应品质，俯仰角速率和舵偏角均处于安全工作范围内，与未考虑异步切换的控制方法相比，本文方法的控制量在异步切换时刻无跳跃现象.

图4 无扰条件下的系统状态随时间变化曲线

图5 无扰条件下的舵偏角随时间变化曲线

为验证控制系统对扰动的抑制能力，在仿真模型中加入Dryden紊流干扰，子系统与控制器异步切换的响应曲线如图6和图7所示.仿真结果表明:控制器具有良好的扰动抑制能力，俯仰角速率和舵偏角均处于安全工作范围内，控制量在异步切换时刻无跳跃现象.

图6 扰动条件下的系统状态随时间变化曲线

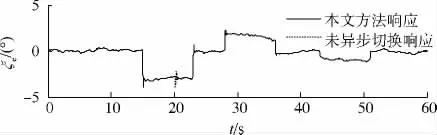
图7 扰动条件下的舵偏角随时间变化曲线

4 结论

本文针对高超声速飞行器子系统与控制器异步切换，提出了一种鲁棒H∞控制策略，构造了依赖于控制器切换信号的Lyapunov函数，有利于异步切换系统的控制器设计，同时也适用于异步切换导致的闭环子系统不稳定情况，放宽了激活子系统能量函数是单调递减的条件，降低设计的保守性，为高超声速飞行器子系统与控制器异步切换方法提供了一种解决思路.仿真结果表明，异步切换鲁棒H∞控制系统体现出良好的动态响应品质，控制量在异步切换时刻无跳跃现象，舵偏角处于安全工作范围内;在模型中加入紊流干扰仿真，控制器体现出具有良好的扰动抑制能力.

References)

［1］ Holland SD，Woods W C，Engelund W C.Hyper-X research vehicle experimental aerodynamics test program overview［J］.Journal of Spacecraft and Rockets，2001，38(6):828 －835

［2］谈树萍，李智斌.高超声速飞行器自适应切换控制及稳定性分析［J］.空间控制技术与应用，2011，37(1):21 －27 Tan Shuping，LiZhibin.Switching control design for a hypersonic flight vehicle［J］.Aerospace Control and Application，2011，37(1):21－27(in Chinese)

［3］宋磊，杨剑影，段志生.多模型切换系统H∞鲁棒控制器的设计与应用［J］.控制理论与应用，2010，27(11):1531 －1536 Song Lei，Yang Jianying，Duan Zhisheng.Design and application of H∞robust controller for multi-model switching system［J］.Control Theory and Applications，2010，27(11):1531 － 1536(in Chinese)

［4］ Hou Yanze，Wang Qing，Dong Chaoyang.Gain scheduled control:switched polytopic system approach［J］.Journal of Guidance Control and Dynamics，2011，34(2):623 －628

［5］张增辉，杨凌宇，张晶，等.基于间隙度量的鲁棒LPV控制律设计［J］.北京航空航天大学学报，2012，38(11):1430－1434 Zhang Zenghui，Yang Lingyu，Zhang Jing，et al.Robust LPV control design using the gap metic［J］.Journal of Beijing University of Aeronautics and Astronautics，2012，38(11):1430 －1434(in Chinese)

［6］ Huang Yiqing，Sun Changyin，Qian Chengshan.Polytopic LPV modeling and gain-scheduled switching control for a flexible airbreathing hypersonic vehicle［J］.Journal of Systems Engineering and Electronics，2013，24(1):118 －127

［7］ Mhaskar P，El-Farra N H，Christ of ides P D.Robust predictive control of switched systems:satisfying uncertain schedules subject to state and control constraints［J］.International Journal of Adaptive Control Signal Process，2008，22(2):161 － 179

［8］ Xie D，Chen X.Observer-based switched control design for switched linear systems with time-delay in detection of switching signal［J］.IET Control Theory Applications，2008，2(5):437 －445

［9］ Zhang Lixian，Shi Peng.Stability l2-gain and asynchronous control of discrete-time switched systems with average dwell time［J］.IEEE Transactions on Automatic Control，2009，54(9):2193－2200

［10］ Zhang Lixian，Gao Huijun.Asynchronously switched control of switched linear systems with average dwell time［J］.Automatica，2010，46(5):953 －958

［11］ Bolender M A，Doman D B.Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle［J］.Journal of Spacecraft and Rockets，2007，44(2):374 －387

［12］ Tan Feng，Duan Guangren，Zhao Lijun.Robust controller design for autopilot of a BTT missile［J］.Proceedings of the 6th World Congress on Intelligent Control and Automation，2006:6358 －6362