非高斯随机分布系统优化控制算法的设计

魏 娇 ， 屈 毅 ，2

（1.咸阳职业技术学院 电子信息系，陕西 咸阳 712000；2.兰州理工大学 电气工程与信息工程学院，甘肃 兰州 730050）

在近三十年来，随机系统控制理论是控制科学与工程研究领域中的一个重要方向。经众多学者多年的研究和发展，随机系统控制已具有完善的理论架构和理论体系，广泛的应用于工业控制中。该理论研究的对象是采用微分方程（或差分方程）描述的动态系统[1-9]。目前，随机系统控制研究的主要成果有线性高斯二次型、马尔可夫参数控制、最小方差控制、自校正控制等内容，其研究的目的是系统变量的统计特性，即通过系统输出均值和方差等统计特性来研究系统的性能指标。但是，当噪声或者干扰不服从高斯分布，系统输出方差和均值就不能描述系统特性。2000年，英国曼彻斯特大学王宏教授针对造纸过程中随机变量不服从高斯分布的假设，提出了系统输出概率密度函数形状控制策略[4-5，9]。近十年来，输出PDF分布控制在的建模和控制算法上有待于完善。我们称输出PDF不服从高斯分布的系统称为非高斯随机分布系统（NGSDS），其对应的控制策略称之为非高斯随机分布控制（NGSDC）[9]。

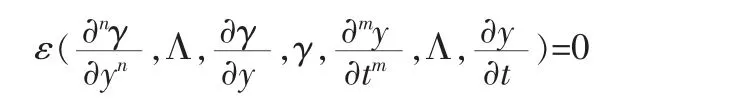
式中ε（·，·）为非线性函数。但在实际应用中，该模型的应用十分困难。因为虽然由机理模型可得偏微分方程，但是模型包含了复杂的自然特性，此外，即使从机理模型得到了偏微分方程，但是控制算法的获得以及实现仍然较为困难[2，3，9]。

如能获到系统变量的概率密度函数γ（y，t），则上述问题可迎刃而解。当噪声或者干扰为高斯过程时，则控制系统输出PDF可认为是高斯随机过程下的PDF控制。但是，当噪声或者干扰不服从高斯分布，系统输出方差和均值就不能描述系统特性。

通过对造纸过程，化工生产过程、食品加工过程中的颗粒尺寸分布（PSD）控制和结晶过程控制等非高斯随机分布系统的控制结构进行抽象，进而可得到图1所示的非高斯随机分布系统结构。

在图1中，非高斯随机分布系统输出为概率密度函数，

在研究随机系统控制时，假设系统变量服从高斯分布或者对称分布。然而，在炉腔燃烧的火焰分布、造纸中的纸张纤维长度分布、粮食加工中的颗粒尺寸分布、化工生产中的分子量分布等许多工业生产过程中，系统变量不服从高斯分布的假设条件。

在上述工业生产过程中，系统变量的分布与系统动态变化紧密相关，但是这些系统变量不满足高斯分布。依据概率知识，系统变量的分布可由概率密度函数来描述。概率密度函数γ（y，t）的动态变化可偏微分方程表示，即

1 问题描述

在随机系统控制研究中，其前提是假设系统中的变量服从高斯分布，例如，在研究最小方差控制时，其控制目标是使闭环系统具有最小方差，即

J=min var（y（t）-r（t））

图1 非高斯随机分布系统结构Fig.1 Non-Gaussian random distribution system architecture

式中 y（t）是系统输出，r（t）表示参考值，var（·）是方差函数。扰动和噪声可以为任意分布的随机过程，控制输入为常规意义的输入。对于 NGSDS，控制目标是使系统输出PDF追踪目标PDF，它突破了随机系统控制研究的局限性，比随机系统控制仅研究系统输出均值和方差更具有普遍性和适用性。

2 优化控制算法

2.1 建立平方根B样条逼近模型

定义 v（t）∈[a，b]是一致连续随机变量，表示非高斯随机分布系统的输出；u（t）∈Rn×1表示系统的控制输入，控制变量v（t）的概率分布。在任何时刻，v（t）可通过其概率密度函数γ（y，u（t））来表示，即

式中 P（a＜v（t）＜y，u（t））是当 u（t）应用于非高斯随机分布系统时，随机变量v（t）的输出PDF。这就意味着系统的输出PDFγ（y，u（t））受系统控制输入 u（t）的控制。

假设定义区间[a，b]是已知的，概率密度函数 γ（y，u（t））是一致连续有界，使用B样条函数逼近，则系统输出PDF的表达式为

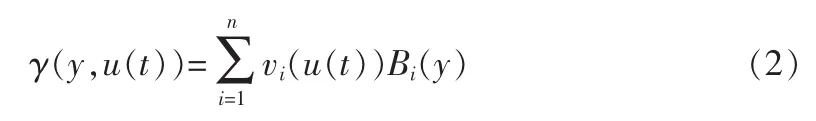
非高斯随机分布系统的动态部分由连续时不变系统表示，则其表达式如下

式中 A∈R（n-1）×（n-1）和 B∈R（n-1）×m是未知的参数矩阵，V（t）=（v1，v2，…，vn-1）是状态向量，w（t）∈Rn-1是外界干扰，C（y），L（t）的定义如下

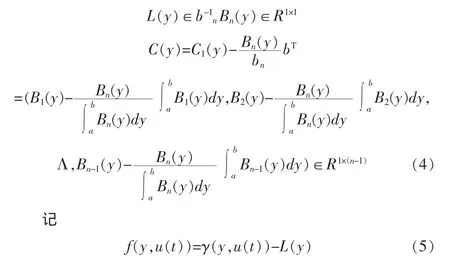
对于 y∈[a，b]，进一步可获得

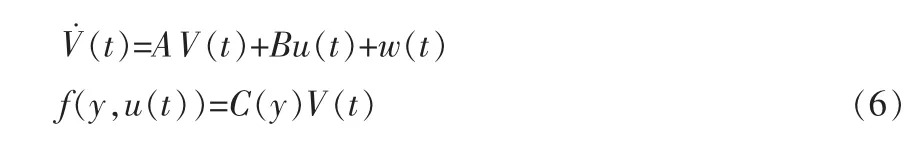
假设存在一个正定常数δ，满足如下表达式

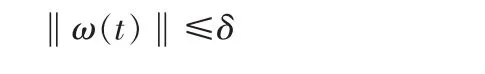
2.2 自适应控制器的设计

在研究非高斯随机分布控制时，控制算法设计的目的是选择输入 u（t）使系统输出 PDF 跟踪目标 PDFγg（y），即

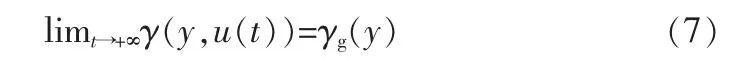
为了实现系统输出PDF追踪目标PDF，定义目标PDF表示如下

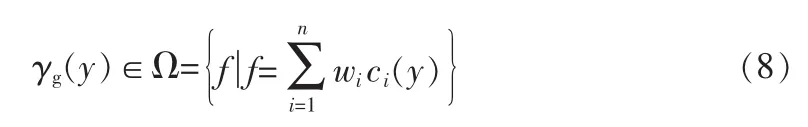
式中 ci（y）是基函数向量 C（y）的第 i个元素，wi（i=1，2，…，n-1）是已知常量。这表示着存在向量Vg∈Rn-1，使目标PDFγg（y）表示如下

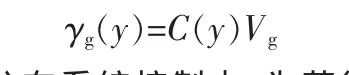
在非高斯随机分布系统控制中，为获得好的动态性能，权值V（t）应追踪目标权值Vg，Vg可从如下参考模型中得到

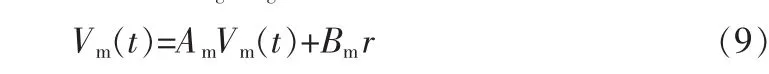
式中 Am∈R（n-1）×（n-1）和 Bm∈R（n-1）×m是已知矩阵，r∈Rm是已知常量。

Am是稳定矩阵，使下列表达式成立

这表示确定系统控制输入 u（t），使 V（t）逼近 Vm（t）。定义

则，可得到误差动态系统

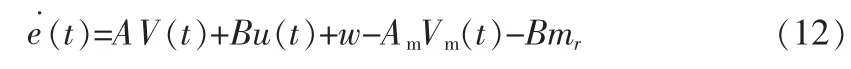
为了使误差动态系统（11）渐近稳定，可构造如下控制算法[1]

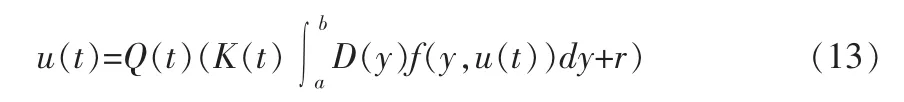
式中 K（t）∈Rm×（n-1）和 Q∈Rm×m已确定的自适应调整增益矩阵，γ（y，u（t））是可测的系统输出 PDF，D（y）∈Rn-1是定义在区间[a，b]上的函数向量，控制输入 u（t）与 PDFγ（y，u（t））的积分相关，定义性能指标为

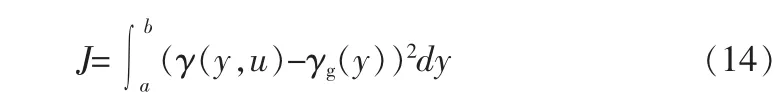
系统性能指标取决于系统 PDFγ（y，u（t））的权值积分。为了简化表达式，定义

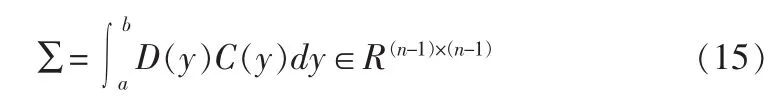
存在两个常数矩阵 K0∈Rm×（n-1）和 Q0∈Rm×m，使下面的条件成立

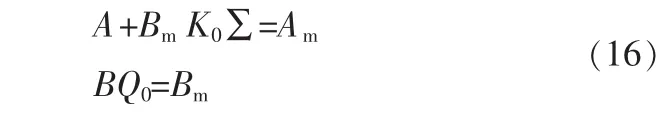
由系统（3）和（13），可得非高斯随机分布闭环系统为

由式（13），（16），（17）可得到误差动态系统

由于 V（t）是不可测的，e（t）也是不可测的，则 e（t）不能在自适应调整算法中使用。必须构造一个信号可在自适应调整算法中使用，则构造的信号为

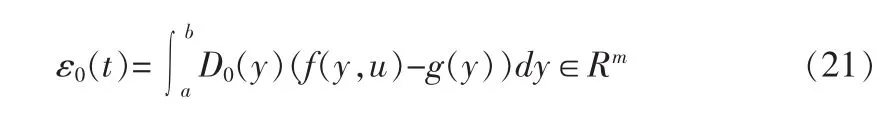
式中D0（y）∈Rm是一个已确定的函数向量，则可看出信号

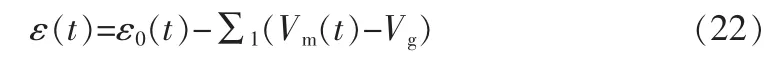
定义

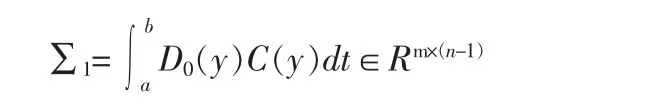
则式（22）可表示为

误差动态系统可进一步表示为

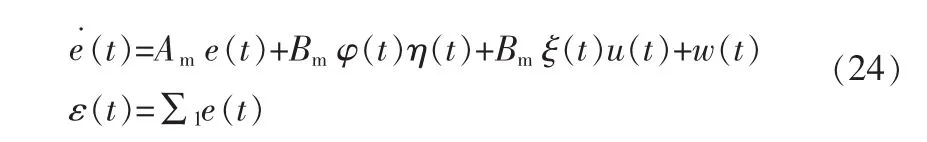
式中除了 e（t），φ（t）和 ξ（t）外，所有参数信息都是可测得。

3 参数 K（t），Q（t）的调整规则

在建立非高斯随机分布误差动态系统（23）之后，接着就需要设计非高斯随机分布系统的控制算法.为了设计K（t），Q（t）的调整规则，本文主要研究在噪声干扰不存在的情况下，通过文献[1，2]直接引出 K（t），Q（t）控制算法。

定理 1:假设Ⅰ式（10），式（16）成立；Ⅱ矩阵 Am稳定和满足 ω（t）=0；Ⅲ存在定义在区间[a，b]上的函数向量 D0（y）和一个正定矩阵P，使表达式

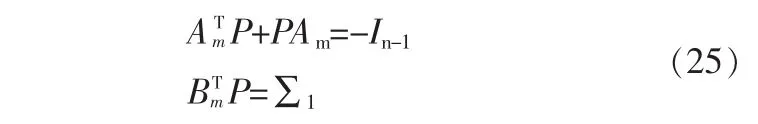
成立，则自适应调整规则

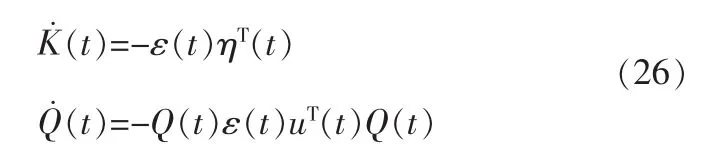
成立，式（24），式（26）中的参数变量一致连续有界且

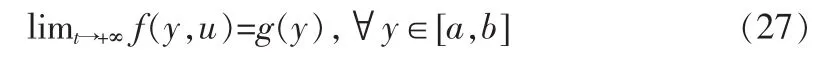
当定理1中的条件满足时，非高斯随机分布闭环系统是全局渐近稳定，可实现式（7）的追踪性能指标。

自适应调整控制算法可通过以下步骤实现：

1）选择 D0（y）使条件（25）满足；

2）采集控制输入u（t），和由系统输出获得概率密度函数γ（y，u（t））；

3）利用方程（5）计算 f（y，u）和参考模型输出 Vm（t）；

4）利用方程（22）计算 ε（t）

5）利用方程（26），计算增益 K（t），Q（t）

6）利用方程（13），计算 u（t）

4 结束语

本文针对非高斯连续随机分布系统提出了一种优化控制算法。首先建立非高斯随机分布系统输出概率密度函数的模型，接着通过系统性能指标得出优化控制算其转化为性能指标最小化问题以及系统的稳定性问题。该控制算法具有较强的稳定性和较好的追踪性能，使非高斯随机分布系统在满足规定的性能指标下，可实现系统输出概率密度函数追踪目标概率密度函数。

[1]屈毅，李战明，李二超.随机分布系统的神经保性能控制器的设计[J].计算机集成制造系统，2012，18（11）:2515-2521.QU Yi，LIZhan-ming，LIEr-chao.Design for guaranteed cost neurocontroiler of stochastic distribution control systems[J].Computer Integrated Manufacturing Systems，2012，18 （11）:2515-2521.

[2]陈海永.随机分布控制及其在焊缝跟踪系统中的可行性研究[D].北京：中国科学院研究生院，2008.

[3]裔杨.随机分布系统跟踪控制与优化算法的研究[D].南京：东南大学，2008.

[4]周靖林.PDF控制及其在滤波中的应用[D].北京：中国科学院研究生院，2005.

[5]姚利娜，王宏.基于有理平方根逼近的非高斯随机分布系统的故障诊断和容错控制[J].控制理论与应用，2006，23（4）:562-568.YAO Li-na，WANG Hong.Fault diagnosis and tolerant control for non-Gaussian stochastic distribution control systems based on the rational square-rootapproximationmodel[J].Journal of control theory and applications，2006，23（4）:562-568.

[6]陈海永，孙鹤旭，王宏.一类仿射非线性系统的概率密度函数形状控制[J].控制与决策，2011，26（8）:1169-1174.CHENHai-yong，SUN He-xu，WANG Hong. Probability density function shape control of a class of affine nonlinear stochastic systems[J].Control and Decision，2011，26（8）:1169-1174.

[7]陈海永，王宏.基于LMI的参数随机变化系统的概率密度函数控制[J].自动化学报，2007，33（11）:1216-1220.CHENHai-yong，WANG Hong.PDF Control of stochastic parameter system using linear matrix inequalities[J].Acta Automatica Sinica，2007，33（11）:1216-1220.

[8]俞立.鲁棒控制—线性矩阵不等式处理方法 [M].北京：清华大学出版社，2002.

[9]屈毅，李战明.非高斯随机分布系统控制与故障检测方法的研究[D].兰州：兰州理工大学，2013.