硬式空中加油未对接系统建模与仿真

刘洋洋，杨朝星，陆宇平

（南京航空航天大学 自动化学院，江苏 南京 210016）

空中加油出现于上世纪初，经过几十年的发展，该技术日臻成熟，目前主要有两种典型形式：软式（插头-锥管式）空中加油和硬式（伸缩管式）空中加油[1]。目前国外学者对硬式加油系统建模已有研究[2-3]，所建模型也较为精确，但其对加油机与伸缩管内部的约束作用没有做具体分析。国内有学者对伸缩管在大气扰动下进行了单独建模[4]；也有学者基于简化的加油系统模型，运用反馈线性化[5]、非对消解耦[6]、特征结构配置[7]等方法研究了伸缩管纵向与横侧向运动的解耦问题。

本文结合国内外学者的相关研究，用牛顿-欧拉法建立了硬式空中加油未对接系统的动力学方程。所建模型将加油机考虑在内，比文献[4]的研究成果更加完整；另外，由于考虑了系统的约束作用，当加油机运动状态改变时，模型能够反映伸缩管运动状态的变化，比文献[5-7]中的简化模型更接近实际加油系统的运动特性；基于以上优点，本文的研究成果能够为空中加油未对接系统的控制方案设计提供一个更好的模型和比较完整的验证依据，更具实际工程应用价值。

1 系统结构及坐标系定义

1.1 系统结构

硬式空中加油系统由加油机、伸缩管、受油机组成，本次建立未对接系统的模型，不考虑受油机，把加油机看成1号刚体，伸缩管看成2号刚体。伸缩管通过万向节与加油机机腹相连，其围绕加油机进行俯仰和滚转运动。

伸缩管的具体结构见图1，由伸缩主管、外伸管、方向舵、升降舵等组成，其结构左右对称，伸缩管与加油机固连的一端称为管头，另一端称为管尾。

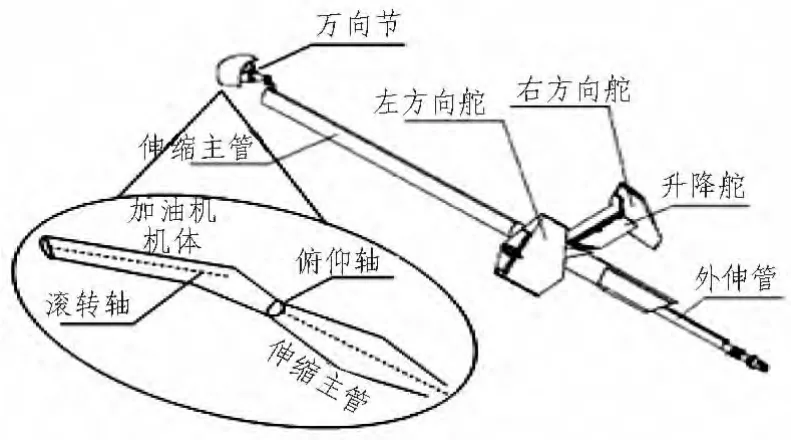
图1 伸缩管结构Fig.1 Boom’s structure

1.2 坐标系定义

伸缩管管体坐标系O2X2Y2Z2：取伸缩管与加油机的铰接点O2作为原点，坐标系与管体固连，O2X2与管体轴线平行并指向管头，O2Y2垂直于伸缩管的对称平面并指向管体右方，O2Z2在伸缩管对称面内与O2X2垂直并指向管体下方。

设!e、1

地面坐标系O0X0Y0Z0按惯性系定义，加油机机体坐标系O1X1Y1Z1按常规飞机所建立的欧美坐标系[8]定义。 设 i→、j→、k軋分别为机体系O1X1轴、O1Y1轴、O1Z1轴的单位向量。

加油机机体坐标系与伸缩管管体坐标系的关系见图2，其中，C为伸缩管的质心，γ1为伸缩管绕其俯仰轴转过的角度，即管体系O2X2轴与机体系O1X1轴的夹角，管头向上为正；γ2为伸缩管绕其滚转轴转过的角度，即管体系O2Y2轴与机体系O1Y1轴的夹角，右滚转为正。

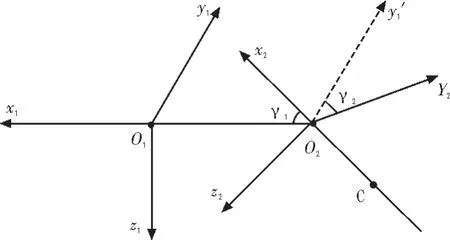
图2 坐标系关系示意图Fig.2 The general view of coordinate system

1.3 相关角度定义

伸缩管管体坐标系相对于加油机机体坐标系的3个角定义为 俯仰角θ21：管体系O2X2轴与O1X1Y1平面所成的角，管头向上为正。

偏航角ψ21：管体系O2X2轴在O1X1Y1平面的投影与O1X1轴的夹角，管尾左偏为正。

滚转角φ21：管体系O2Z2轴与O2X2轴、O1Z1轴所组成的平面的夹角，右滚转为正。

加油机的俯仰角 θ1、偏航角 ψ1、滚转角 φ1、迎角 α1、侧滑角β1按照常规飞机对应角度定义[8]。伸缩管的俯仰角θ2、偏航角 ψ2、滚转角 φ2、迎角 α2、侧滑角 β2类似于常规飞机对应角度的定义。

根据以上定义，可得出各坐标系间的转换关系，机体系到地面系的转换矩阵与常规飞机到地面的转换矩阵相同；管体系到地面系的转换矩阵类似于机体系到地面系的转换矩阵。伸缩管围绕加油机做俯仰和滚转运动，可得机体系到管体系的转换矩阵，另外，也可以用θ21、ψ21、φ21表示机体系到管体系的转换矩阵。

2 牛顿-欧拉法动力学方程推导

2.1 建模假设

伸缩管本身是一个具有三自由度的刚体，但由于俯仰和滚转是伸缩管运动的主要模态，且伸缩运动对模型结构影响不大，建模时可以先不考虑伸缩管的伸缩运动。本次建模不考虑大气紊流和干扰风梯度对系统的影响。

2.2 系统动力学方程推导

2.2.1 伸缩管的力方程组

伸缩管所受的力包括重力、空气动力、加油机对其的约束力，求出这3个力在管体系中的分量，运用牛顿第二定理可求出伸缩管的力方程组。

2.2.2 伸缩管的力矩方程组

伸缩管受到的外力对质心的力矩有空气动力矩、约束力产生的力矩、约束力偶矩。

约束力偶矩M→12方向垂直于俯仰轴和滚转轴所组成的平面，其大小设为 Mk，则

设伸缩管质心在管体系下的坐标为（-rc0 0），则约束力产生的力矩为

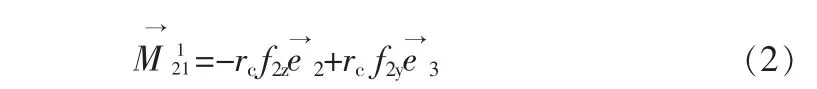
根据动量矩定理可得伸缩管的力矩方程组为

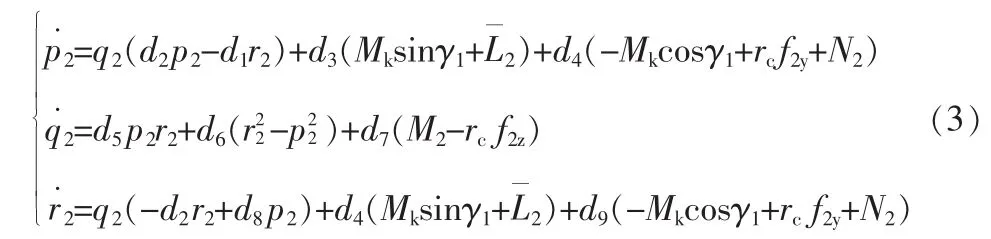
2.2.3 伸缩管的运动方程组

依据飞机相对地面运动方程组的推导过程，可得伸缩管相对飞机的运动方程组为

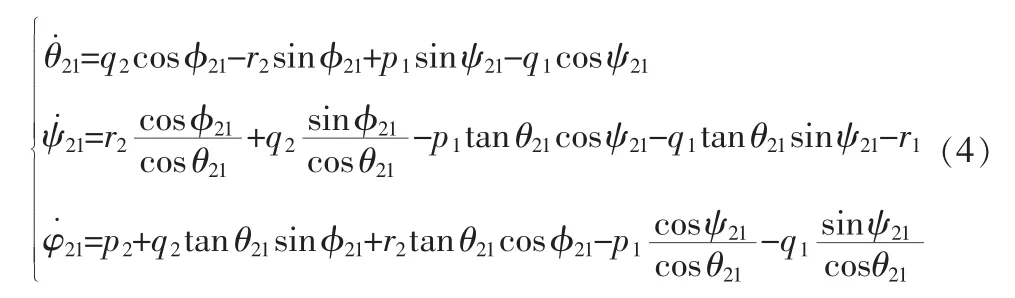
2.2.4 加油机的力方程组

加油机所受的力包括重力、空气动力、发动机推力，伸缩管对其的约束力，求出这4个力在机体系中的分量，运用牛顿第二定理可求出加油机的力方程组。

2.2.5 加油机的力矩方程组

加油机受到的外力对质心的力矩有空气动力矩、约束力产生的力矩、力偶矩。

力偶矩M→21在机体系下为

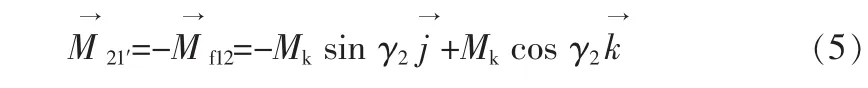
设伸缩管铰接点在机体坐标系中的坐标为 （x10 z1），则约束力矩为

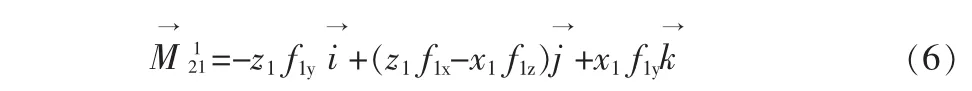
根据动量矩定理可得加油机的力矩方程组为

其中，L¯1、M1、N1和 f1x、 f1y、 f1z，分别为空气动力矩和约束力在机体系 3个轴的分量，p1、q1、r1为加油机的角速度 Ω1在机体系 3 个轴的分量，ci（i=1，2，...，9）是与加油机转动惯量和惯性积相关的系数[8]。

2.3 约束方程与解约束

2.3.1 系统约束方程

设伸缩管与加油机的相对速度为v→21，由加油机的质心速度v→1和伸缩管质心速度v→2的关系可得

对式（8）求导整理可得

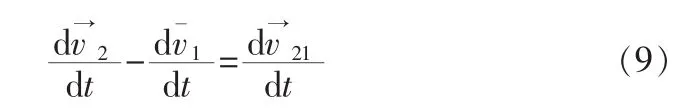
相对速度可由下式表示

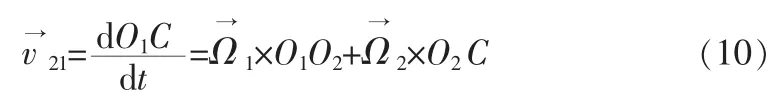
运用牛顿第二定理求出式（9）等号左边的项，将各项求导表达式转换在机体系下，可得出约束方程。

2.3.2 系统约束求解

下文推导过程中出现的 Bi（i=0，...9）、B˙j（j=0，...5）是 θ21、ψ21的函数表达式，D0是 p1、q1、r1、q2、r2、θ21、ψ21的函数表达式，介于篇幅，不再详细列出。

由机体系到管体系的转换关系可得

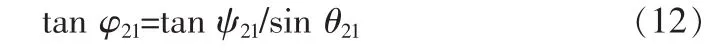
对式（12）求导可得

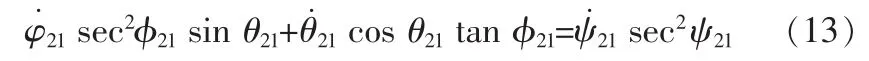
将式（4）代入并化简可得

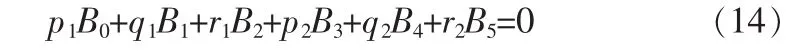
对（14）求导可得

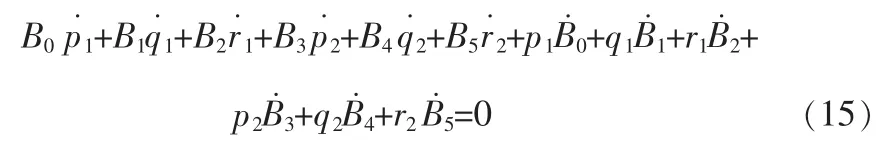
将式（3）、（7）代入式（15）化简可得

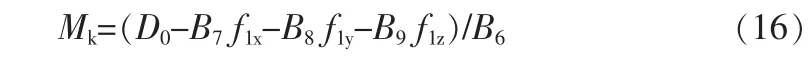
将式（3）、（7）、（16）代入约束方程中，运用克莱姆法则可求解出约束力，将求解出的约束力代入式（16），可求解出约束力矩。至此，系统解约束完成。

对式（10）求导可得

3 模型仿真分析

加油机的质量与伸缩管的质量比约为250:1，飞行高度约为6 000 m，飞行马赫数约为0.4。用加油机迎角、平尾偏度、油门偏度、伸缩管升降舵偏度进行配平。配平状态下加油机的俯仰角为1.833 5°，伸缩管的俯仰角为30°。

3.1 加油机对伸缩管的影响

3.1.1 加油机对伸缩管纵向运动的影响

系统初始状态处于平衡点，起始时刻正偏加油机升降舵1°，维持一秒后恢复至平衡处。θ1与s1的响应曲线如图3所示。

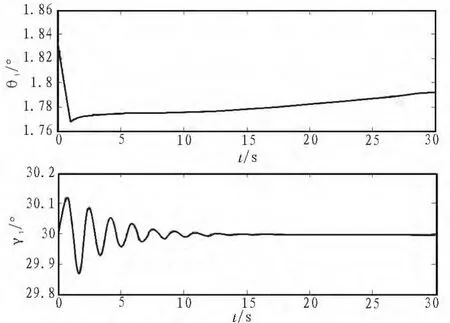
图3 加油机升降舵引起的系统俯仰角响应Fig.3 Response curve of pitch angle caused by the tanker’s elevator

3.1.2 加油机对伸缩管横侧向运动影响

系统初始状态处于平衡点，起始时刻正偏加油机方向舵1°，维持一秒后恢复至平衡处。φ1与γ2的响应曲线如图4所示。

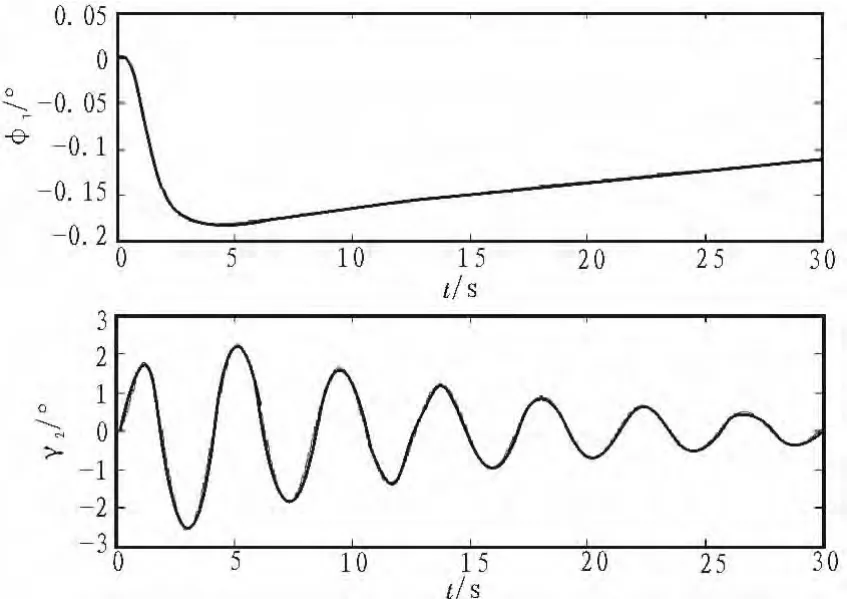
图4 加油机方向舵引起的系统滚转角响应Fig.4 Response curve of roll angle caused by the tanker’s rudder

由图可见，正如前文所述，加油机的受扰运动对伸缩管的运动产生了很大的影响。在飞行过程中，加油机的舵面即使有较小变化，其影响传递至伸缩管都可能成倍放大。

3.2 伸缩管对加油机的影响

3.2.1 伸缩管对加油机纵向运动的影响

系统初始状态处于平衡点，起始时刻正偏伸缩管升降舵5°并保持。θ1与γ1的响应曲线如图5所示。

3.2.2 伸缩管对加油机横侧向运动影响

系统初始状态处于平衡点，起始时刻正偏伸缩管方向舵5°并保持。φ1与γ2的响应曲线如图6所示。

由图可见，伸缩管舵面偏转，其相应角运动有较大的变化，加油机相应的角运动变化远不及伸缩管显著，说明伸缩管确实对加油机的运动产生了影响，但由于二者质量悬殊，该影响并不明显。

3.3 伸缩管的运动耦合

系统初始状态处于平衡点，起始时刻正偏伸缩管的升降舵2°并保持，在第15 s时正偏其方向舵5°并保持。γ1与γ2的响应曲线如图7所示。

图5 伸缩管升降舵引起的系统俯仰角响应Fig.5 Response curve of pitch angle caused by th boom’s elevator

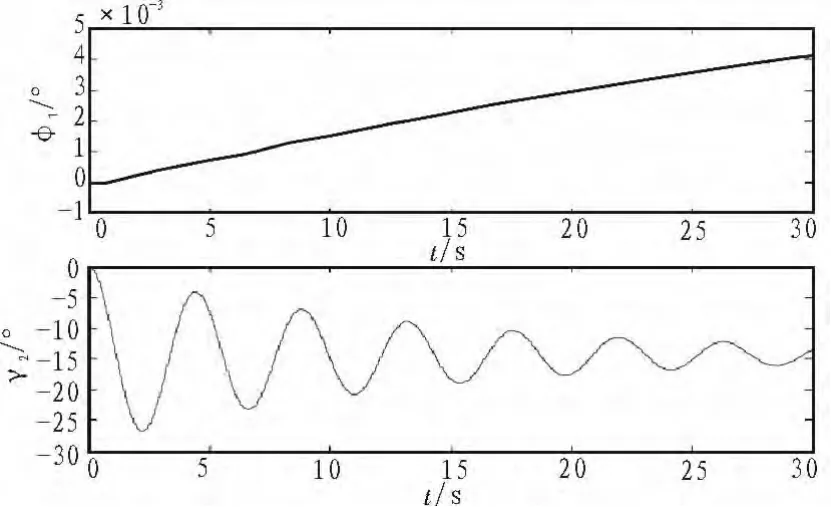
图6 伸缩管方向舵引起的系统滚转角响应Fig.6 Response curve of roll angle caused by the boom’s rudder

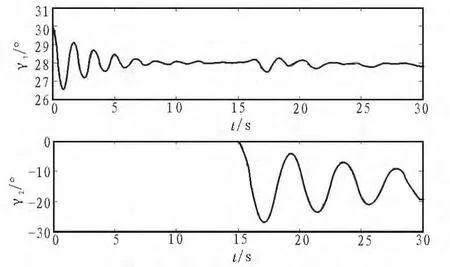
图7 伸缩管舵面偏转时其角运动响应Fig.7 Response curve of boom’s anglemovement caused by its rudder and elevator

由图可见，由于伸缩管方向舵的偏转，其俯仰角响应在稳定后又出现较强的振荡现象，说明伸缩管的横向与纵向运动间存在耦合；另外，伸缩管角运动响应振荡收敛，说明伸缩管具有稳定性，但阻尼比较低，动态特性较差。

4 结 论

本文将硬式空中加油未对接系统视作由加油机和伸缩管通过万向节连接而成的两刚体系统，分析了两刚体的运动特点，由其质心速度关系得出系统约束方程，根据万向节的结构及安装特点，对约束方程进行求解，建立了系统动力学方程。基于所建模型的特点，在下一步设计系统控制律时应考虑加油机所受扰动及伸缩管运动解耦等问题。

[1]W Mao F O Eke.A survey of the dynamics and control of aircraft during aerial refueling[J].Nonlinear Dynamics and System Theory，2008，9（4）:375-388.

[2]Jeremy JSmith，Donald LKunz.Simulation of the dynamically coupled KC-135 tanker and refueling boom[C]//modeling and simulation Technologies Conference，Hilton，South Carolina:AIAA，2007:1-10.

[3]Austin L S，Donald L K.Dynamic coupling of the KC-135 tanker and boom for modeling and simulation[R].AFRLVA-WP-TP-2006-342，2006.

[4]薛建平，陈博，王小平.空中加油伸缩套管控制研究[J].飞行力学，2008，26（4）:14-18.XUE Jian-ping，CHEN Bo，WANG Xiao-ping.Control law research on aerial refueling boom[J].FlightDynamic，2008，26（4）:14-18.

[5]黑文静，安刚，林皓.输入输出非线性反馈线性化方法在硬式空中加油控制系统设计中的应用 [J].航空学报，2008，29（3）:652-656.HEIWen-jing，AN Gang，LIN HAO.Input-output feedback non-linearzation used in design of boom air-refueling control system[J].Acta Aeronautica Et Astronautica Sinica，2008，29（3）:652-656.

[6]曲耀红，陈丽莎，仇江.非对消解耦方法在硬式空中加油管控制中的应用[J].火力与指挥控制，2010，35（10）:171-173.QU Yao-hong，CHEN Li-sha，QIU Jiang.Application of noncancellation decoupling in boom refueling Control[J].Fire Control&Command Control，2010，35（10）:171-173.

[7]陈丽莎，贾秋玲，张贤雷.基于特征结构配置的硬式空中伸缩管解耦设计[J].计算机仿真，2010，27（11）:28-31.CHEN Li-sha，JIA Qiu-ling，ZHANG Xian-lei.Decoupling design of refueling boom by output feedback eigen structure assignment[J].Computer Simulation，2010，27（11）:28-31.

[8]吴森堂，费玉华.飞行控制系统[M].北京:北京航空航天大学出版社，2005.