基于Chirp-z变换的电波流速仪的测量精度研究

李秀丽，刘纪元，焦学峰，陈飞虎

（1.沈阳航空航天大学 电子信息工程学院，辽宁 沈阳 110136；2.中国科学院 声学研究所综合声纳实验室，北京 100080；3.北京航瑞博泰科技有限公司 北京 100102）

近年来，随着电子技术的发展，也加快了水利系统现代化建设的发展进程。在明渠监测方法中，非接触式测量方法由于以其测量速度快，安装安全方便等特点逐步成为发展的主流趋势，特别适用于含沙量大，淤泥较多的渠道。非接触式测量的主流产品是电波流速仪。

电波流速仪是用雷达多普勒效应来测量水流速度的，其主体思路是将雷达原理和信号处理结束相结合。而考虑到我们所要测定的是水流的速度，所以选 择使用连续波雷达来实现。即利用发射信号与回波信号的多普勒频率差来提取速度信息。

1 电波流速仪的原理

如图1所示，雷达照射水面时，部分电磁波被水面散射，且只有向后散射的那部分电磁波能量构成回波信号，其余电磁波则折射入水。由于波浪底下的水流集体作为波浪的载体，具有和波浪相同的运动速度，所以波浪上的回波产生的多普勒频移必然会反应水面流速，我们将接收到的信号频率相对与发射的信号频率关系定义为：

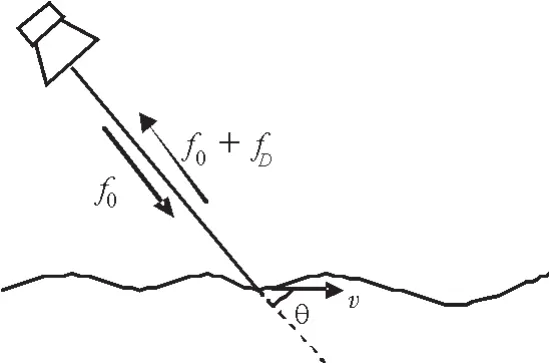
图1 原理图Fig.1 s diagram

其中，fD为多普勒频率；f0为发射频率；fr为接收到的回波频率。

多普勒频率与速度之间的关系表示为：

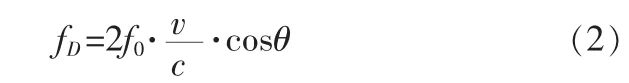
由式（2）可以推出：

其中，fD为多普勒频率；f0为发射频率；v为水流速度；c为光速；θ为水流方向与雷达发射器到运动目标连线之间的角度。由式（3）可以看出，只要从回波信号中提取出多普勒频偏就能求得水流的速度。

假设连续波雷达发射一个频率为f0的0信号：

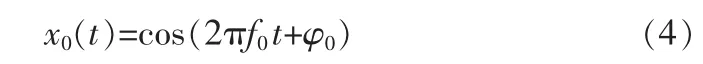
经过时间t1后，雷达接收机接收到该信号，接收到的信号表示为：

将 x1（t）与本振信（t）=e-j（2πfDt+φ0）号混频，来去除高频分量，最终得到的中频信号为：

经过采样，我们可以的到：

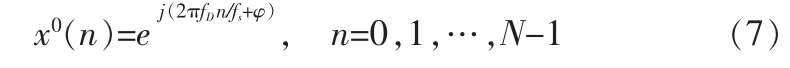
式中，fs表示采样频率，N表示采样点数。进行离散频谱分析可知，用ip表示谱峰处对应的谱线号，则测量所得的多普勒频率可以表示为：

则，所得到的水流速度表示为：

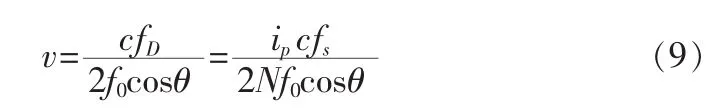
从式（9）可以看出，水流速度与离散频谱谱峰值的谱线号，采样频率，采样点数有关，该式为多普勒雷达频域测水流速度的基本公式[2]。

从上式我们可知，测速的精度主要取决于离散频谱分析提取多普勒频移的精度。一般测速雷达提取频移的方法是进行FFT，但是由FFT得到的离散频谱谱线，目标多普勒频率对应谱线通常会落到两条谱线之间，从而产生一定的测速误差。若用fD表示多普勒频率测量值，用f′D表示目标的真实多普勒频率，则由于栅栏效应所造成的目标多普勒频率最大误差可以表示为：

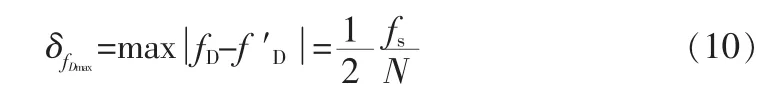
如果改为用速度表示，则水流速度的最大误差为：

从（12）式我们可以看出：

1）如果不采取适当的措施，测速的误差会比较大的，不满足系统精度要求。

2）由上式可以看出，要想减小FFT所引起的测速误差，可以使采样因子K的取值应尽可能小，或是采样频率要尽可能的低，但前提是必须满足采样定理的要求，即K≥2。

3）只要适当增大FFT的采样点数N，也可以达到所要求的测速精度。但是在实际应用时，FFT的采样点数由于受到处理器件和系统实时性等因素的制约，不可能无条件地增大，所以这种方法受到一定的限制。

4）选择合适的频谱校正算法可以进一步提高测速的精度。如果采用Chirp-z变换能够对回波频谱中的指定部分进行局部细化，这样就能够实现在采样点数，运算量增加不多的情况下，大大提高雷达的测量精度[2-3]。

2 Chirp-z变换

线性调频z变换算法[4]是计算螺旋线周线上z变换的诸取样，这些取样在螺旋线的某一部分上按等角度分布，设x（n）表示N 点序列，其 z变换表示为 X（z），则给定点 Zk上的 X（zk）为：

其中 A=A0ejθ0，Zk=AW-k，W=W0ejφ0，A0和 θ0分别为第一个取样点位置的半径和角度，其他采样是沿螺旋周线按角度间隔φ0分布；W0控制周线盘旋的倾斜度，W0＞1，周线向内盘旋，W0＜1，周线向外盘旋，W0=1，表示螺旋线是一段圆弧；A0=1，表示这段圆弧是单位圆的一部分[5]。

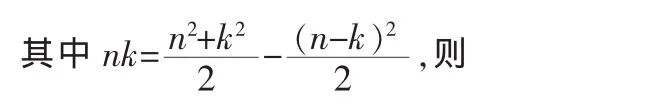
注：*表示卷积，所以最终可以表示为：

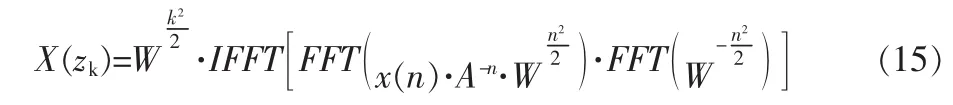
Chirp-z变换与FFT相比，不同之处在于，它是对一段z平面上的螺旋线进行等间隔采样，而FFT是对整个单位圆进行采样。为了在不增加运算量的前提下提高测量精度，我们先对回波信号进行FFT全景谱分析，进行谱峰搜索找到最大的值，然后在最大值附近范围进行Chirp-z变化，从而得到更加精确的频谱值[6]。

3 数据分析

3.1 仿真数据处理

根据所给的数据可以算出水流速度的真实值为：

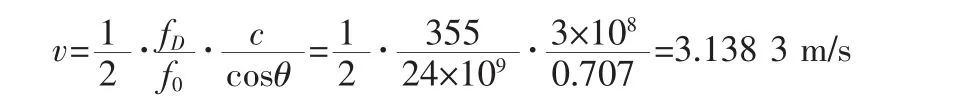
用FFT处理后所测得的水流速度值为：

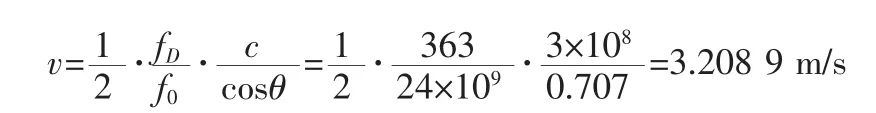
可得误差为0.070 6m/s，而是用了Chirp-z变换处理后的水流速度为：

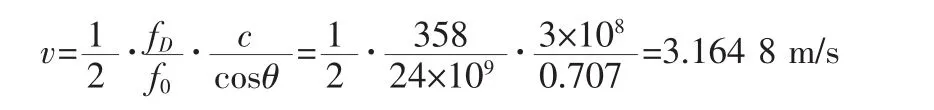
可得误差为0.026 5 m/s，我们可以看出与FFT相比，经过Chirp-z变换处理后的测量精度要高很多。图2分别为经过FFT与Chirp-z变换的matlab仿真图。

同样的方法，我们分别进行了不同速度的测量，测得的4组数据如下表所示。

3.2 结果分析

通过对不同流速时采集到的回波信号进行处理，对所得到的的测量结果进行对比我们可以看出，在不改变采样点数的情况下，使用Chirp-z进行局部细化的测量方法所得到的测量精度比仅对回波信号使用FFT时提高很多。

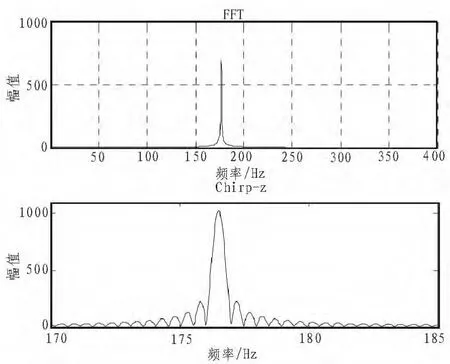
图2 经过FFT与Chirp-z变换的频谱仿真图Fig.2 Simulation diagram of processing spectrum by using FFT and Chirp-z

表1 FFT与Chirp-z处理后的测试数据Tab.1 Test data of processing the signal by using FFT and Chirp-z

4 结束语

近年来，电波测流仪以其安装安全方便，测速快等特点已经在我国得到了迅速的发展和推广。但对于测量的精度仍有可以提升的空间，所以在电子技术不断发展的今天，电波流速仪必定可以进一步提高完善，成为明渠测流的核心力量。

[1]吕宗城.电波流速仪在山区河流推算流量应用分析[J].广西水利水电，2012（6）:6-8.LV Zong-cheng.Application of electric wave flow velocity meter in mountainous area river current calculation[J].Guangxi Water Resources&Hydropower Engineering，2012（6）:6-8.

[2]丁康，谢明，杨志坚.离散频谱分析校正理论与技术[M].北京:电子工业出版社，1995.

[3]冯志华，刘永斌，张健.用在频谱细化中Chirp-Z变换的特性分析[J].信号处理，2006，22（5）:741-745.FENG Zhi-hua，LIU Yong-bin，ZHANG Jian.Character analyses of the Chirp-Z transformation used in the spectrum zooming[J].Signal Processing，2006，22（5）:741-745.

[4]徐飞，王延暴.Chirp-z变换在雷达信号处理中的应用[J].现代电子技术，2011，34（9）:28-29.XU Fei，WANG Yan-bao.Application of Chirp-Z transform in radar signal processing[J].Modern Electronics Technique，2011，34（6）:28-29.

[5]丁康，潘成灏，李巍华.ZFFT与Chirp-z变换细化选带的频谱分析对比[J].振动与冲击，2006，25（6）:9-12.DING Kang，PAN Cheng-hao，LIWei-hua.Spectrum analysis comparison between ZFFT and Chirp-Z transform[J].Journal of Vibration and Shock，2006，25（6）:9-12.

[6]冯维婷.Chirp-Z变换在CW雷达高精度速度测量中的应用[J].电子科技，2007（9）:6-7.FENGWei-ting.Application of Chirp-Z transform in velocity measurement of CW radar[J].Slectronic Science and Technology，2007（9）:6-7.