窄带干扰下基于子空间跟踪的扩频序列估计
马 超,张立民,林洪文
(海军航空工程学院 电子信息工程系,山东 烟台 264001)
直接序列扩频信号由于抗截获能 力强、抗干扰能力强和抗多 径干扰能力强等优点,在现代军事和非军事通信中已获得广泛应用。通信对抗中,对直扩方式的研究成为热门课题,对直扩信号扩频序列盲估计的研究有重要的意义。文献[1-4]研究了利用m序列的三阶相关特性估计扩频通信信号的m序列的问题。文献[5]提出了一种基于特征值分解的方法估计伪码序列,在文献[6-7]中进一步对其性能做了的分析,并把矩阵的特征值分解抽象为主分量分析问题,然后通过神经网络的方法求解特征向量,来降低运算复杂度。但是对DS/SS信号,特别是长码扩频信号,构造特征矩阵并进行特征值分解,需要的存储空间和计算量非常大,严重影响着这一技术的发展和应用。以上算法都是针对加性高斯白噪声信道提出的,窄带干扰环境下的伪码盲估计问题一直是一个研究难点。对于存在窄带干扰的通信信号,一般情况下,在对扩频序列估计之前,都要先对窄带干扰进行抑制。
文中提出了一种基于快速子空间跟踪的窄带干扰下扩频码序列估计算法。该算法首先利用滑动窗技术取得码同步,然后应用压缩投影近似子空间跟踪(PASTd)技术实现窄带干扰的消除和对PN码的估计。由于该算法避开了矩阵的特征值分解,所以大大降低了存储量和运算量。由于DSSS信号易于解调,笔者采用了基带DS信号,并根据工程实际假设一位信息码由一周期PN码序列调制,且PN码序列与信息码同步。
1 信号模型
文中研究的直接序列扩频窄带干扰环境下接收信号为:

式中n(t)是功率谱密度为的零均值加性高斯白噪声。s(t)为基带DSSS信号

j(t)表示接收信号中的窄带干扰,以多音干扰为例

式中Am表示第m个干扰的幅度;Ωm表示干扰频率与直扩信号中心频率的频差;θm表示相位,其值等于在0到2π之间均匀分布的随机数。
2 特征值分解法
假设信息码dm的码元宽度Ts已知,将接收信号式(1)按Tc周期采样,划分成多个窗口宽度为Ts非重叠数据窗。令y表示一个窗口内的信号抽样矢量,则y必定跨越2个信息码,即y可写为:

式中,j表示窄带干扰抽样矢量;n表示高斯白噪声抽样矢量;T0为失步点(0<T0<Ts),则

其中 Bk=[b1,b2,…,bM]是一个 N×M维矩阵 bl=a=[A1,A2,…AM]T,nk=[nk-1,nk-2,…,nk-N]T。
因此,向量yk的自相关矩阵可以表示为

将式(4)带入式(10),有

可知,所得u1和u2是正交归一化向量。
窄带干扰jk可以表示为

在以上的推导过程中

sm=[sin ilΩmTC,sin i2ΩmTC,…,sin iNΩmTC]T
式中,矩阵I是维数为N的单位矩阵。
3 子空间跟踪算法
r(r<P)维信号子空间的最大特征向量可以由以下代价方程求最小值得出
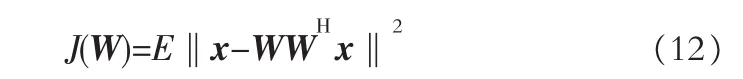
式中:x和W分别表示信号向量和权值向量。在文献[8]中已经证明,当且仅当W=UrQ时,J(W)取得全局最小值,这里Ur包含相关矩阵R的r个主特征向量,Q是任意的酉矩阵。重新修改代价方程如下


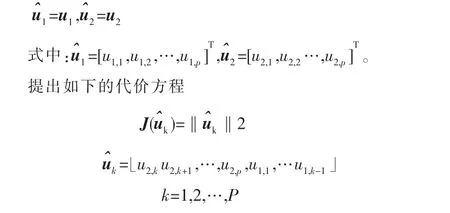
021
式中:用 y(i)=WT(i-1)x(i)近似y(i)=WT(i)x(i),然后应用 RLS准 则迭代求出收敛权值,这时的W(n)就是自相 关矩阵R的主特征向量。以上就是分离主分量的近似子空间跟踪技术[8]。在这里我们可以利用压缩投影 近似子空间跟踪(PASTd)[8]算法来简化PAST技术,从数据向量中减去在该最大特征向量上的投影,那么次大特征向量就称为更新数据中的主特征向量。重复该过程,直到估计出 所有的r维的特征向量。
基于信号子空间跟踪算法有以下几个特点:
1)PAST算法计算复杂度是O(Pr),应用到窄带干扰下扩频码序列估计就是r=2(M+1),因此只需求出前2(M+1)个特征向量。
2)不需求出自相关矩阵R(P×P),大大减少了计算量。
3)不需求出特征分解的特征值。
下面提出一种取得码同步的新方法——滑动窗技术,此法只需求出两个有用信号的特征向量,据此即可估计非同步延迟值和PN码序列,而不需求出相关矩阵特征值。排序。
非同步延迟值和PN码序列的估计可以由以下公式求出

根据以上理论分析,我们可以得出基于PAST算法的结构框图如图1所示。
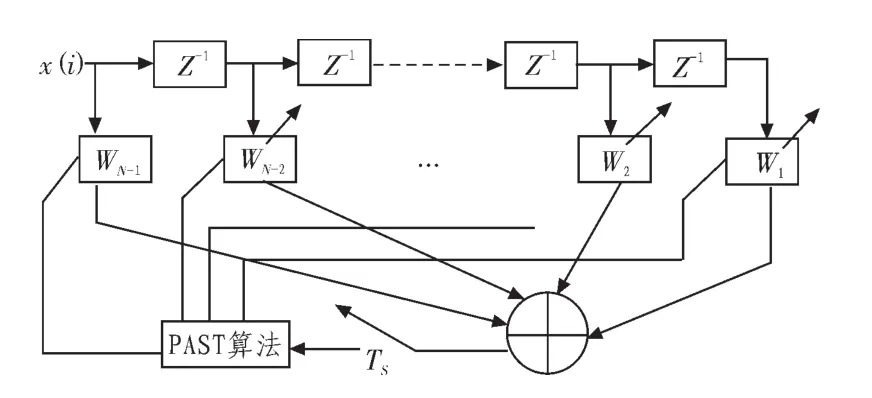
图1 基于PAST算法的原理图Fig.1 diagram of PAST algorithm
基于子空间跟踪的窄带干扰直扩序列盲估计算法的具体步骤如下:
步骤1 以采样率Tc对接收信号每Ts采样一组数据,并且得到矢量yk=[xk-1,xk-2,…xk-N]T;
步骤 2 合理初始化 di(0)和 wi(0)

4 仿真实验及分析
实验中采用的2个窄带干扰分别为:
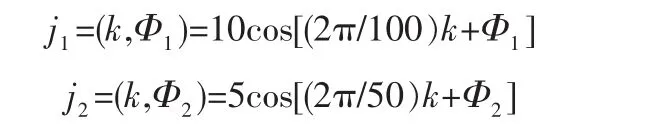
式中每次产生的窄带干扰数据向量j=j1(Φ1)+j2(Φ2),k=1,2,…,126,即长度为 126 bit,Φ1和 Φ2为在[0,2π]上均匀分布的不同随机数。
实验1 DS/SS信号采用BPSK调制,P=63,采用m序列。观测采样数据组数N=200,窗长度为Ts,采样间隔Tc,非同步延迟值T0=44Tc。信噪比SNR=-8 dB,信噪比计算采用公式101g(σs2/σn2)(σs2为信号方差)。 由于有两个窄带干扰,所以前 4个特征向量为两个窄带干扰。图2是基于子空间跟踪算法估计的最大和次大特征向量对应了窄带干扰1,图3基于子空间跟踪算法估计的第3和第4特征向量对应了窄带干扰2。图4和图5对应的是有用信号的特征向量序列。图6是同步后估计的伪码序列,图7是原始m序列。可以看出,窄带干扰下基于子空间跟踪的PN码估计算法能消除窄带干扰并且准确地恢复原m序列的信息。

图2 最大和次大特征值对应的向量序列Fig.2 Vector sequence corresponding to largest and second largest eigenvalues
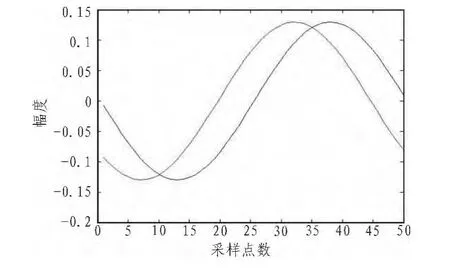
图3 第3和第4特征值对应的向量序列Fig.3 Vector sequence corresponding to third and fourth largest eigenvalues
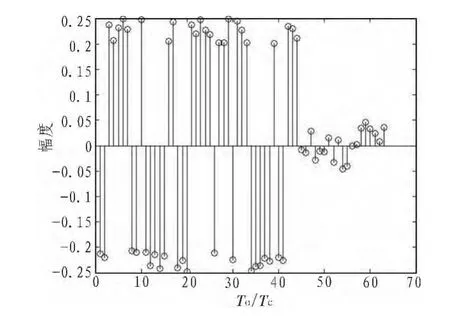
图4 第5特征值对应的向量序列Fig.4 Vector sequence corresponding to fifth largest eigenvalue

图5 第6特征值对应的向量序列Fig.5 Vector sequence corresponding to sixth largest eigenvalue

图6 同步后的估计序列Fig.6 Synchronized estimation sequence
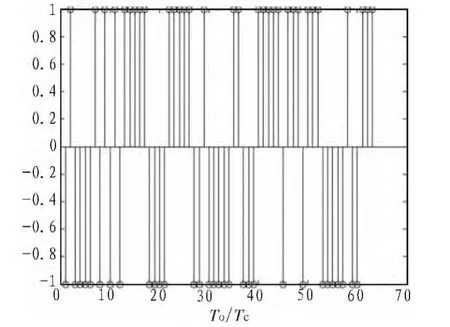
图7 原始m序列Fig.7 Originalm-sequence

图8 不同信噪比和码长下的恢复正确率Fig.8 Recovery of the correct rate under different SNR and code length
实验2 DS/SS信号采用BPSK调制,采用m序列。观测采样数据窗长度为Ts,采样间隔Tc。选取了码长分别为31,63和127 的 m 序列,信噪比设为-6 dB,-9 dB,-10 dB,-12 dB,-14 dB,-15 dB,-17 dB,-18 dB,-20 dB,各自经过了 100 次计算得出的数据。
5 结束语
文中提出了一种窄带干扰下基于子空间跟踪实现扩频序列盲估计的方法。该方法利用改进的滑动窗技术取得码同步后,再利用增强的子空间跟踪算法获得所需向量序列,并基于此消除窄带干扰和恢复出扩频码序列。该方法在性能上优于已有神经网络算法,并且相较于EVD算法还具有低存储量、低运算量,易于硬件实现的特点。
[1]Batty K E,Adams E R.Detection and blind identification of m-sequence codesusing higher order statistics[J].Proceedings of the IEEESignalProcessingWorkshop,1999:16-20.
[2]ZU Yun xiao.The Detection and Recognition of DS-SS Signals Using Higher-Order Statistical Processing[C].ICSP2006 Proceedings,2006:2022-2025.
[3]俎云霄.基于高阶统计处理技术的m-序列检测及识别[J].电子与信息学报,2007,29(7):1576-1579.ZU Yunxiao.The Detection and Recognition ofm-sequence Based on Higher Order Statistical Processing Techniques[J].Journal of Electronics&Information Technology,2007,29(7):1576-1579.
[4]苏绍景,伍文君,黄芝平,等.含错m序列本原多项式的高阶统计测定算法[J].兵工学报,2010,31(12):1593-1598.SU Shao-jing,WU Wen-jun,HUANG Zhi-ping,et al.High-order statistics determination algorithm ofm-sequence containing the wrongprimitive polynomial [J]. Acta Armamentarii,2010,31(12):1493-1598.
[5]Burel G,Bouder C.Blind estimation of the pseudo-random sequence of a direct sequence spread spectrum signal[C].IEEE:Milcom 2000 21st century military communications conference proceeding,2000:967-970.
[6]张天骐,林孝康,周正中.基于神经网络的低信噪比直扩信号扩频码的盲估计方法 [J].电路与系统学报,2007,12(2):118-123.ZHANG Tian-qi,LIN Xiao-kang,ZHOU Zheng-zhong.The blind estimation based on neural network of DSSS signal spreading code in Low SNR [J].Journal of Circuits and Systems,2007,12(2):118-123.
[7]赵德芳,张天骐,金翔,等.基于BP神经网络的直扩信号扩频码盲识别[J].电讯技术,2010,50(10):28-35.ZHAO De-fang,ZHANG Tian-qi,JIN Xiang,et al.The blind estimation based on BP neural network of DSSS spreading code[J].Telecommunication Engineering,2010,50(10):28-35.
[8]Yang B.Projection approximation subspace tracking[J].IEEE Trans.on Signal Processing,1995,43(1):95-107.

