矩阵光学中的琼斯矩阵方法与其在偏振光中的应用

何启浩

(西南民族大学电气信息工程学院, 四川 成都 610041)

矩阵光学中的琼斯矩阵方法与其在偏振光中的应用

何启浩

(西南民族大学电气信息工程学院, 四川 成都 610041)

分析和探讨了线偏振光、椭圆(圆)偏振光和常用起偏方法与偏振光学器件以及矩阵光学中的琼斯矩阵方法, 结合一些实例的计算与分析, 探讨了偏振光的叠加与合成和偏振光通过组合偏振光学器件后出射光的偏振态, 进一步分析和探讨了琼斯矩阵在偏振光中的应用.

偏振光; 矩阵光学; 琼斯矩阵与应用

矩阵光学是将矩阵应用于光学, 这对于描述和表述一些繁琐的光学问题(例如几何光学计算、薄膜干涉等)以及解决一些实际光学问题提供了方便和有效方法[1-2]. 1941年美国物理学家琼斯(R.C.Jones)提出了任意偏振光可以由它的光矢量的两个分量构成的一个列矩阵来表示, 这个列矩阵称为琼斯矢量[3-9]. 用琼斯矩阵描述光的偏振态及其叠加与变换, 不仅形式简洁, 而且可以方便地计算得到偏振光通过不同组合的偏振光学器件后出射光的偏振态. 本文分析和探讨了偏振光和琼斯矩阵的方法, 结合一些实例的计算与分析, 探讨了琼斯矩阵在偏振光中的应用.

1 偏振光

1.1 线偏振光(平面偏振光)和椭圆(圆)偏振光

光矢量在光传播中始终保持在一个固定平面上振动的光称为线偏振光(也称平面偏振光). 椭圆(圆)偏振光是指光矢量绕着光的传播方向旋转, 光矢量的端点轨迹是一个椭圆(圆). 椭圆(圆)偏振光可分解为两束振动方向相互垂直的、不等幅(等幅)的、相位差恒定的线偏振光的叠加. 有右旋椭圆(圆)偏振光与左旋椭圆(圆)偏振光.

1.2 常用起偏方法与偏振光学器件

1.2.1 偏振片

某些物质(例如硫酸碘奎宁晶体、电气石等)[3-7]能吸收某一方向的光振动, 而只让与这个方向垂直的光振动通过, 这种性质称二向色性. 偏振片是以利用晶体的各向异性对某一方向的光振动有强烈吸收; 另一方向可以通光(称为偏振化方向 ). 偏振片既可用于“起偏”; 也可用于分析、检验光束的偏振状态, 即“检偏”.

1.2.2 光在各向异性介质中的传播“起偏”

双折射起偏: 一束光入射到具有各向异性的晶体媒质(如方解石、石英等)[3-4]中分成两束(e光,o光)光的现象称为双折射现象. 光在这种晶体内沿光轴传播时无双折射. 其余情况则均得到两束分开的线偏振光. 用双折射晶体可制成各种波片和补偿器. 例如沃拉斯顿(Wollston)棱镜、尼科耳(Nicol)棱镜; 巴俾涅(Babinet)补偿器等.

1.2.3 光在两种介质界面上的反射“起偏”

当自然光在两种介质界面上反射和折射后变为部分偏振光的现象: 反射光中垂直于入射面光矢量的分量比例大; 折射光中则平行于入射面光矢量的分量比例大. 当入射角 i 变, 反射光、折射光的偏振度也变. 当自然光以布儒斯特角(起偏振角)ib入射时[3-9]: 反射光为线偏振光, 光矢量振动方向垂直于入射面.

2 偏振光和偏振光学器件的琼斯矩阵

2.1 偏振光的琼斯矩阵

2.1.1 线偏振光琼斯矩阵(归一化形式)[3-7]

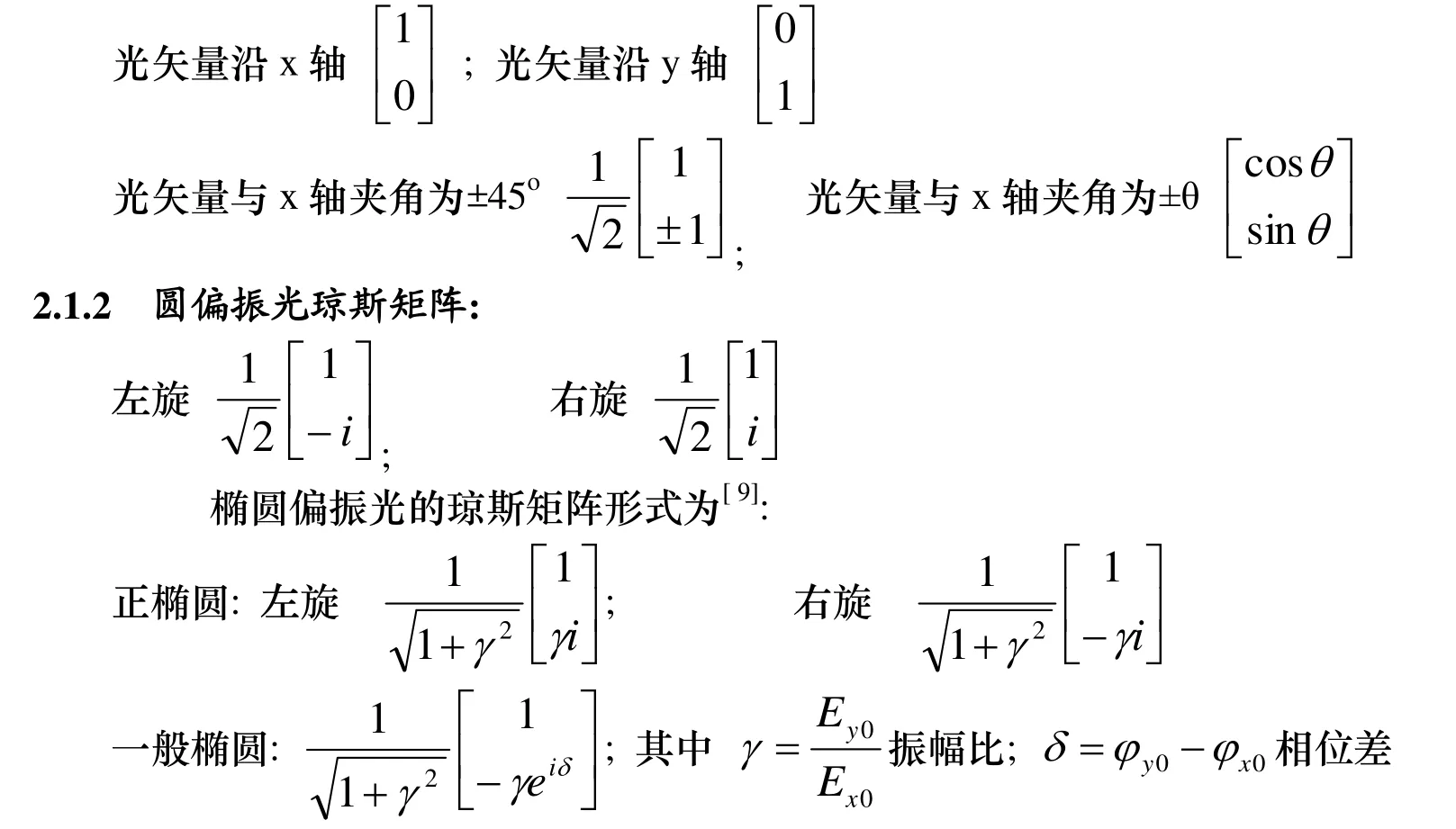
2.2 常用偏振光学器件的琼斯矩阵[3-7]

2.2.1 线偏振器

2.2.2 1/4波片

2.2.3 圆偏振器

3 琼斯矩阵在偏振光中的应用

光的偏振性使光增加了一个可被调控的自由度——偏振态; 通过适当的偏振光叠加与合成以及适当的偏振光学器件的组合与光路设计, 可进一步将光的偏振态按设计的要求去改变. 因此, 计算不同偏振光的叠加与合成以及光通过不同的偏振光学器件后的偏振态是偏振光应用的一个重要的前题. 用琼斯矩阵描述光的偏振态及其叠加与变换, 不仅形式简洁, 而且可以方便地计算得到光通过不同的偏振光学器件组成的复杂系统后出射光的偏振态, 也便于使用计算机快速计算.

3.1 偏振光的叠加与合成

讨论右旋圆偏振光和左旋圆偏振光的叠加与合成, 从2.1.2中的圆偏振光琼斯矩阵, 应用琼斯矢量计算可得:叠加的结果是线偏振光, 光矢量方向沿x轴, 振幅是圆偏振光振幅的两倍.

计算长、短轴之比为2:1, 长轴沿x轴的右旋椭圆偏振光和左旋椭圆偏振光的叠加与合成, 其右旋和左旋椭圆偏振光的琼斯矢量分别为:

合成的结果是线偏振光, 光矢量方向沿x轴, 振幅是椭圆偏振光长轴振幅的四倍.

3.2 偏振光通过组合偏振光学器件后出射光的偏振态

在复杂的光路中, 如果偏振光相继通过n个偏振光学器件, 它们的琼斯矩阵分别为G1, G2, …, Gn, 由矩阵相乘法则[10], 出射光的琼斯矩阵为:

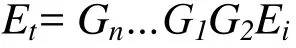
计算光矢量沿x轴的线偏振光相继通过快轴与x轴夹角为45o一1／4波片和快轴在x轴方向另一1／4波片, 出射光的琼斯矩阵为:

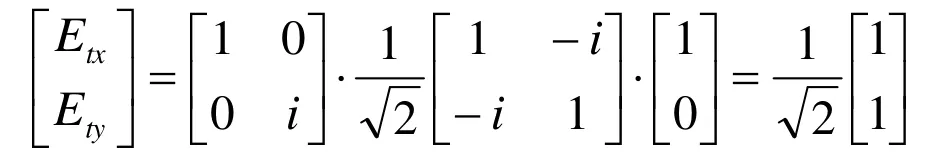
从计算结果可知, 出射光为光矢量与x轴夹角为45o的线偏振光, 但光振幅不变.

计算一右旋圆偏振光相继通过快轴在y轴一1／4波片和右旋圆偏振器后, 再通过一透光轴在x轴的线偏振器, 则出射光的琼斯矩阵为:

从计算结果可知, 出射光为光矢量沿x轴的线偏振光, 其光振幅与原右旋圆偏振光振幅相等.

4 结束语

从以上的分析与讨论和几个实例的计算分析中可以看出, 用琼斯矩阵描述光的不同偏振态和不同的偏振光学器件, 不仅形式简洁明了, 而且可以方便地使用矩阵运算法则(矩阵的加法和乘法)计算得到光的偏振态及其叠加与变换, 也可以方便地计算得出光通过由不同偏振光学器件组成的复杂系统后出射光的偏振态. 但是, 琼斯矩阵不能用于描述自然光和部分偏振光, 这对于它在光学中的应用中受到一定的限制. 对于描述自然光和部分偏振光, 可以运用斯托克斯矢量表示法[5], 但用该方法在处理偏振光时计算较繁琐[5]. 对于处理由自然光、部分偏振光和不同偏振光的叠加与变换计算时, 以及自然光、部分偏振光通过由不同偏振光学器件组成的复杂系统后出射光的偏振态的计算时, 笔者认为可以分别运用琼斯矩阵方法和斯托克斯矢量表示法计算, 具体的处理方法和混合计算有待于进一步的探讨和研究.

[1]季光明. 矩阵光学中变换矩阵的推导[J]. 成都理工大学学报: 自然科学版, 2003(2): 107-110.

[2]郭淑玉. 论矩阵光学中的ABCD矩阵及其应用[J]. 江汉大学学报, 1992(6): 23-28.

[3]宋贵才. 物理光学理论与应用[M]. 北京: 北京大学出版社, 2010: 259-267.

[4]谢敬辉. 物理光学教程[M]. 北京: 北京理工大学出版社, 2005: 317-319, 348-354.

[5]廖延彪. 光学原理与应用[M]. 北京: 电子工业出版社, 2006: 34-36, 258-261.

[6]叶玉堂. 光学教程[M]. 北京: 清华大学出版社, 2005: 343-350.

[7]姚启钧. 光学教程[M]. 4版. 北京: 高等教育出版社, 2010: 259-2650.

[8]普朝光. 光波光学[M]. 北京: 国防工业出版社, 2013: 406-411.

[9]韩军. 工程光学[M]. 北京: 国防工业出版社, 2012: 133-137.

[10] 居余马. 线性代数[M]. 2版. 北京: 清华大学出版社, 2002: 49-54.

Method of Jones matrix of matrix optics and its application in polarized light

HE Qi-hao
(School of Electrical and Information Engineering, Southwest University for Nationalities,Chengdu 610041, P. R. C.)

This paper analyses and discusses the principle and method of linearly polarized light, elliptically(circularly) polarized light, polarizing methods and polarizing devices in common use, and Jones matrix of matrix optics and the composition of polarized light. The polarization state of polarized light passing through polarizing devices and the application of Jones matrix in polarized light are further discussed with some examples.

polarized light; matrix optics; Jones matrix and application

O436

A

1003-4271(2014)05-0772-04

10.3969/j.issn.1003-4271.2014.05.26

2014-07-24

何启浩(1959-), 男, 汉族, 重庆人, 副教授; 研究方向: 光学.