埋地储罐结构设计与ANSYS数值模拟

俞然刚，刘浩，宋龙杰，祝晓晓，农漪，朱海

中国石油大学（华东）储运与建筑工程学院，山东青岛266580

埋地储罐结构设计与ANSYS数值模拟

俞然刚，刘浩，宋龙杰，祝晓晓，农漪，朱海

中国石油大学（华东）储运与建筑工程学院，山东青岛266580

文章总结了埋地储罐结构设计方法，分析了其受力特点，针对储罐的特殊工况提出了采用ANSYS软件进行数值模拟的方法。结合具体设计实例，介绍了在结构设计之后，利用ANSYS软件进行建模加载计算得出储罐在覆土外压作用下的变形及应力分布规律的方法。对比分析理论计算与数值模拟结果，验证了数值模拟结果的正确性，指出常规稳定性设计的不合理之处，说明了数值模拟作为储罐结构设计的参考和补充的必要性。

埋地储罐；结构设计；ANSYS；数值模拟；变形；应力

0 引言

卧式埋地储罐常用于储存汽油、柴油、液化石油气等燃料，广泛应用于油库、加油加气站等场所。其优点在于能够承受较高的正压和负压，可在工厂预制后运往现场安装，有利于减少油品的蒸发损耗，消防要求低，隐蔽且节约占地。我国经济发展迅速，能源需求不断加大，作为常用储油容器的埋地储罐数量日趋增加，这无疑会构成重大危险源和水质、土壤污染源[1]。对于卧式埋地储罐结构设计，目前尚无专业设计标准和规范。在国内，其结构主要依据GB150-2011《压力容器》[2]进行设计，国外也都依据本国的压力容器规范[3]进行设计。然而，这些标准规范都是针对一般的压力容器建立起来的，虽然具有广泛的参考性，但缺乏针对性，设计工程师很难把握其可靠性。基于此，本文总结了埋地储罐的结构设计方法，提出了数值模拟的方法，并结合具体实例，进行结构设计计算和ANSYS的数值模拟，对比分析这两种计算结果，探讨了埋地储罐结构设计的可靠性，以期为工程设计提供参考。

1 埋地储罐的结构设计

埋地储罐置于地下，受到内压、覆土外压及本身自重等外力作用。此外，还可能受到地下水浮力和地面载荷（包括动载荷、静载荷）的作用。若有地下水浮力，则需要在储罐结构设计完成后进行抗浮验算；若存在地面载荷，可将其等效成均布载荷，并转化为土层厚度（当量土层厚度[4]）来计算；设计计算时，储罐的埋深应为实际埋深与当量土层厚度之和。

1.1 强度设计

埋地储罐强度设计[2，5-6]主要用于确定储罐壁厚。由于作用在罐上的土压力抵消了部分应力，覆土外压对储罐受力有利，因此可不考虑外压，按照GB150-2011内压圆筒相关公式计算储罐壁厚。

圆筒壁厚计算公式：

圆筒应力计算公式：

式中δ——圆筒计算厚度/mm；

P——储罐设计内压/MPa；

Di——圆筒内径/mm；

[σ]t——圆筒材料在设计温度下的许用应力/MPa；

φ——圆筒焊缝系数；

σ——圆筒计算应力/MPa；

δe——圆筒有效厚度/mm。

计算厚度及厚度附加量求和圆整后即为圆筒的名义厚度，应符合最小厚度和刚度要求，名义厚度除去厚度附加量即为有效厚度。厚度附加量包括腐蚀裕量和钢板厚度负偏差，取值依据GB150-2011相关规定。考虑制作成品要求，封头厚度一般比圆筒厚度大2 mm。

1.2 稳定性设计

埋地储罐除承受内压外，还承受四周的覆土压力，此压力使储罐趋于变形失稳，所以对于储罐除进行强度计算外，还应进行稳定性校核[2，5-6]。稳定性校核公式：

式中[P]——许用外压/kPa，根据储罐内压强度得到的有效壁厚和加强圈设置情况，按GB150-2011相关规定确定；

Pc——计算外压/kPa。

认为圆筒最大压力作用点在距离通过圆心水平轴1/3R处[6]，将此最大压力作为计算外压，其计算公式：

式中γ——土体重度/（kN/m3）；

R——圆筒半径/m；

H0——储罐埋深，即地面距罐顶的距离/m；

K0——土的侧压力系数，碎石土K0=0.18～0.25，沙石土K0=0.25～0.33，黏土K0=0.33。

2 埋地储罐ANSYS数值模拟方法

对于结构的数值模拟，目前常用的软件是ANSYS有限元软件，其建模方便，计算精度高。土体为弹塑性材料，力学性质及本构模型复杂，ANSYS中能用于岩土材料的模型只有DP模型，对土体的计算结果不理想甚至不收敛。因此，本文考虑将储罐上部覆土转换为荷载，利用ANSYS软件实现对储罐比较精确的数值模拟。储罐圆筒承受内压能力强，而在外压作用下容易失稳破坏，故埋地储罐在空罐状态下比较危险，模拟中不考虑内压。

2.1 埋地储罐受力特点

储罐所受周围土压力作用可分为两部分，即径向力和切向力的作用。根据国内外相关研究[7-9]，可知其分布如图1所示。

图1 埋地圆筒周围填土作用力分布[7]

图1中的左、右两图分别为填土在不同压实度下的实验结果，反映了不同压实度的填土对罐壁的作用力分布规律，二者基本相同。从图1中可以看出，圆筒上半部左、右1/4圆筒，径向力由上至下先增大后减小，最大值发生在中间段；切向力在起始点为零，向下逐渐增大达到最大值，后又逐渐减小，至终点（与X轴交点）上方附近为零；从该点至终点，切向力方向逆转，沿切向向上，大小逐渐变大，但此段圆弧长度较短，且切向力值较小，可不予考虑；因此，切向力可近似为从上部起始点零值逐渐增大到最大，再减小至终点为零。圆筒上半部所受切向力与径向力相比，不可忽略；下半部切向力较小，可忽略其影响，认为只受地基径向支撑作用；因此，在进行ANSYS建模时，圆筒下半部可通过SHELL63单元参数弹性地基刚度（Elastic foundation stiffness，EFS）模拟地基支撑作用，圆筒上半部土体作用可转化成径向力和切向力并同时施加在模型上。

一般情况下，埋地储罐设计应考虑地面载荷。地面载荷按均布载荷考虑，将其等效为一定厚度的土层。因此，存在地面载荷的埋地储罐，其上覆土层厚度可取实际埋深与当量土层厚度之和，然后转化成径向力和切向力。

2.2 径向力和切向力计算公式推导

储罐承受上部土压力如图2所示。

图2 圆筒受力分析图

罐体上半部承受的土压力连续作用在罐壁上，求出埋深为H时罐体上某一点（χ，y）的土压力σ（与Y轴的夹角为θ）大小，然后再将其沿圆筒径向和切向分解。点（χ，y）与圆筒圆心的连线与X轴成α夹角。圆筒径向力σn和切向力στ计算公式推导结果见式（5）、（6）、（7）。

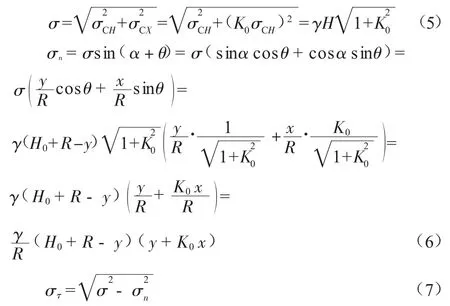
在圆筒上半部分选取若干个点，将每一点的坐标值代入上述公式中，求出该点径向力σn和切向力στ，将所有点σn和στ值进行拟合，得其近似函数表达式（关于χ或y的函数，方便ANSYS加载）。将函数表达式输入到ANSYS中，利用表面效应单元SURF154，同时加载径向力和切向力进行计算。

3 设计举例及数值模拟

某埋地储罐，其圆筒内径为3 m，长度为10 m，封头为半球形封头；罐体材料为Q235-B，设计内压为0.1 MPa，设计温度下许用应力[σ]t为113 MPa，焊缝系数φ为0.85；腐蚀裕量C1=1 mm，钢板厚度负偏差C2=0.25 mm；储罐埋深1.5 m，土体重度为18 kN/m3，土体侧压力系数K0=0.3。

3.1 结构设计

3.1.1 强度计算

储罐设计内压为0.1 MPa，按照式（1）计算得圆筒壁厚δ=1.563 mm，厚度附加量C=C1+C2=1.25 mm，则两者的和δ′=2.813 mm，不包括腐蚀裕量的最小厚度应不小于3 mm[2]，且为考虑刚度，通常情况下要求最小厚度δmin≥2Di×10-3=6 mm[10]，故取圆筒名义厚度δn=6 mm，则其有效厚度δe=δn-C=4.75 mm，封头名义厚度δn′=8 mm。由式（4）计算得到外压Pc=46.98 kPa，由式（2）可计算得到外压作用下的圆筒应力σ=14.87 MPa，设计内压作用下圆筒应力σ= 22.27 MPa。

3.1.2 稳定性设计

按上述强度设计，圆筒名义厚度δn=6 mm，有效厚度δe=4.75 mm；圆筒外径Do=3 000+2×6= 3 012 mm；假设不设加强圈，则圆筒计算长度[2]L=10 +2×2/3×1.5=12（m），故L/Do=3.984，Do/δe= 634；由文献[2]可查得A=0.000 021，且A值小于设计温度曲线的最小值，则许用外压[P]的计算公式为[2]：

式中A——外压应变系数；

E——钢材弹性模量/GPa。

计算得许用外压[P]=4.42 kPa＜Pc（46.98 kPa），故需要设置加强圈，且壁厚取值偏小。适当增加壁厚值，取δn=8 mm，则δe=6.75 mm，加强圈间距取为2 m，按照上述方法计算各项参数，得到许用外压[P]= 69.35 kPa＞Pc，故可依次确定各项参数的数值。加强圈截面选用矩形截面，尺寸选用b（宽）×h（高）= 16 mm×80 mm，根据相关文献所给计算方法[2，11]，可验证加强圈尺寸满足设计要求。考虑腐蚀裕量1 mm，加强圈截面两边各加宽1 mm，因此加强圈尺寸确定为b×h=18 mm×80 mm。

3.2 ANSYS数值模拟

ANSYS建模计算，罐体下半部通过SHELL63单元设置参数弹性地基刚度EFS模拟地基支撑作用，上半部通过SURF154单元同时施加径向力和切向力。

3.2.1 径向力

如图2所示，在第一象限1/4圆筒上，y坐标每隔1/15R选取一个计算点，将每个点坐标χ，y代入式（5），计算出每一点处罐壁所受径向力。表1为各点处罐壁所受径向力，图3为径向力二次拟合曲线（关于y的函数），函数表达式为σn=-15.847y2+31.845y+15.965。

表1 罐壁不同位置处径向力分布

图3 罐壁径向力关于y的变化曲线

3.2.2 切向力

由式（6）可得各点处罐壁所受切向力。由理论知识可知，在y=0和y=R处，切向力为零，即罐壁上M、N点（见图2）不受切向力作用，但在M、N点附近，切向力不为零。为避免出现切向力突变，假定在区间（0，2R/15）和（13R/15，R）内切向力为线性变化。在区间（2R/15，13R/15）内，对切向力变化曲线进行拟合，曲线及其函数表达式见图4。由拟合曲线方程στ=-36.656 y+56.176可知，当y=2R/15=0.2时，στ=48.84 kPa，即曲线通过（2R/15，48.84）点；当y=13 R/15=1.3时，στ=8.52 kPa，即曲线过（13 R/15，8.52）点。为确保整个区间上曲线的连续性，分别将折点y=2R/15和y=13R/15处的στ值修正为48.84 kPa和8.52 kPa。因此，各点处罐壁所受切向力如表2所示。

综上所述，罐壁所受切向力函数表达式如下：

3.2.3 计算结果分析

无加强圈罐体变形及应力（单位：Pa）分布见图5，有加强圈罐体应力分布见图6，加强圈的应力分布见图7、图8。

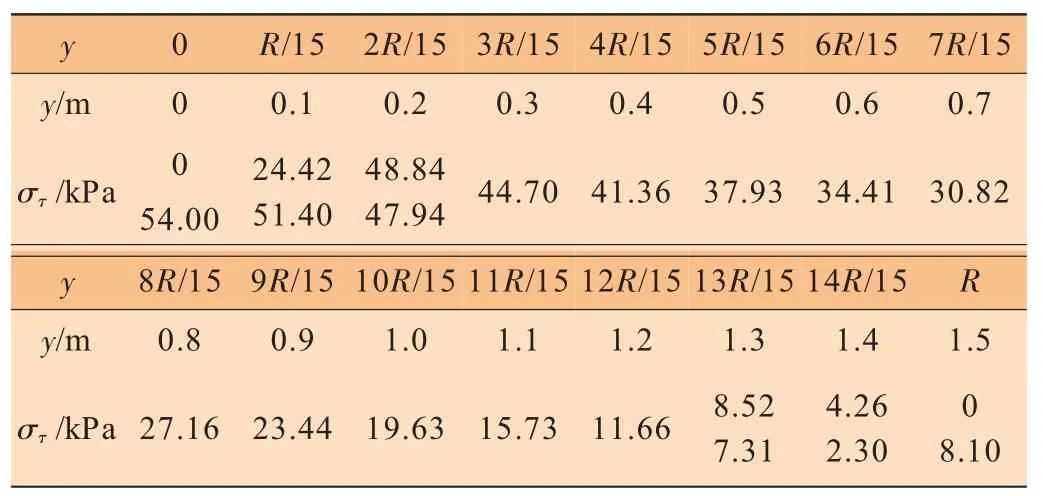
表2 罐壁不同位置处切向力分布

图4 罐壁切向力关于y的变化曲线

图5 无加强圈罐体变形及应力分布

图6 有加强圈罐体变形及应力分布

图7 罐体中部加强圈变形及应力分布

图8 罐体端部加强圈变形及应力分布

由图5可知，无加强圈罐体最大变形为9.956 mm，发生在罐体中部的罐顶；罐体上部被整体压陷，两侧凸起，压陷程度从两端到中间逐渐加深。由图6可知，有加强圈罐体最大变形为4.806 mm，变形趋势同无加强圈罐体。对比可知，无加强圈罐体变形比有加强圈罐体的变形大很多。

由图5可知，无加强圈罐体最大应力为80.7 MPa，产生在罐体上下两部分交界处；罐体上部两侧凸起处应力也较大，罐顶应力大小次之，封头和罐底应力都较小。整体上看，大应力都集中在交界处及其附近区域，而罐体其他部位应力都较小，应力分布不均匀。

由图6可知，有加强圈罐体最大应力为62.4 MPa，产生在交界处与中部加强圈相接的罐体上，且在交界处罐体应力都较大。整体上看，罐体应力分布较均匀，避免了局部应力较大而大部分罐体应力较小的现象。

由以上分析可知，设置加强圈既能有效减小罐体的变形，又能避免罐体局部出现大应力，改善应力分布的不均匀性，因此设置加强圈对提高埋地储罐的稳定性及改善储罐受力性能具有重要作用。另外，封头的变形及应力都很小，因此在储罐设计中，可以考虑封头与圆筒同厚，无需加厚2 mm。

关于加强圈的变形和应力，由图7可知，罐体中部加强圈最大变形为4.808 mm，最大应力达到134 MPa，比有加强圈罐体最大应力62.4 MPa大很多。由图8可知，罐体端部加强圈最大变形为2.044 mm，最大应力为39.8 MPa。中部加强圈的应力变形都比端部加强圈要大很多，因此在进行加强圈设置时，不同部位的加强圈可以考虑采用不同的截面形式或尺寸，从而提高材料利用率，节约钢材。

3.3 理论计算与数值模拟结果对比分析

通过数值模拟得出，罐体第一主应力分布如图9所示。

图9 罐体第一主应力分布

由图9可知，ANSYS计算所得罐体的第一主应力最大值为70 MPa，但大应力都集中在罐体上半部两侧凸起的小区域内，罐体大部分区域的应力都在7.69 MPa以下（图中蓝色区域）。

埋地储罐在均匀分布的计算外压作用下的应力为10.47 MPa，数值模拟得出储罐在不均匀覆土外压作用下的应力分布如图9所示，外压的不均匀性导致罐体局部区域出现较大的应力，但大部分罐体的应力都略小于计算外压作用下的应力，两种计算结果相互印证。因此，ANSYS的计算结果是正确的，且更好地反映了埋地储罐在实际工况下的受力情况。

储罐埋置在地下时罐壁受到土体所产生的不均匀径向力和切向力的作用。依据GB150-2011的稳定性校核要求，直接将储罐的稳定性简化为受均匀外压（取罐壁最大土压力）圆筒的稳定性，未考虑外压不均匀性及罐壁切向力的作用；另外，取罐壁最大土压力作为圆筒外压，与其实际受力大小相差较远。因而，埋地储罐稳定性设计方法太过简化，偏离储罐实际工况较远，设计工程师很难把握其设计结果的可靠性。通过数值模拟，可计算出储罐在不均匀覆土外压作用下的变形，根据变形大小并结合经验，设计工程师可初步判定储罐是否会发生失稳破坏，因此ANSYS数值模拟结果可作为结构设计的参考和补充。但从根本上来说，变形大小并不能真正反应储罐的稳定性[12]，应从理论计算方法上进行稳定性设计的完善。

4 结论

（1）埋地储罐在覆土外压作用下，罐体上部被整体压陷，两侧凸起，压陷程度从两端到中间逐渐加深；罐体两侧凸起部位会产生比较大的应力，而罐体其他部位应力都非常小，储罐应力分布不均匀。

（2）封头的应力及变形都较小，设计中可取封头与圆筒同厚，也方便制造成品。

（3）设置加强圈既能有效减小罐体的变形，又能避免罐体局部应力过大，改善应力分布的不均匀性，提高材料利用率，节约钢材。

（4）埋地储罐稳定性设计偏于简化，与实际工况相差较远，难以把握设计结果的可靠性，但通过数值模拟获得储罐变形大小，再结合工程经验，设计工程师可初步判定储罐失稳与否，数值模拟能更好地反映埋地储罐在实际工况下的受力情况，ANSYS数值模拟结果可作为结构设计的参考和补充。

[1]刘扬，赵洪激，董家梅.常压储罐系统可靠性研究[J].石油学报，2002，23（5）:96-100.

[2]GB150-2011，压力容器[S].

[3]ASME Boiler&Pressure VesselCode 2007（SectionⅧDivision 1），Pressure Vessels[S].

[4]白顺果，崔自治，党进谦.土力学[M].北京:中国水利水电出版社，2009.

[5]宋吉胜.地埋式油罐的设计[J].石油工程建设，2002，28（3）:4-7.

[6]王立平.卧式埋地油罐设计[J].油气田地面工程，2007，26（6）:40-41.

[7]Itzhak S，Naftali G.Soil stress distribution around buried pipes[J]. Journalof Transportation Engineering，1986，112（5）：481-494.

[8]Senro K，Balvant R.Pipe-soil interaction analysis of field tests of buried PVC pipe[J].Journalof Infrastructure Systems，1996，2（4）：119-120.

[9]帅健，王晓霖.地面占压荷载作用下的管道应力分析[J].中国石油大学学报（自然科学版），2009，33（2）:99-108.

[10]JB 4710-2005，钢制塔式容器[S].

[11]李世玉，桑如苞.压力容器工程师设计指南[M].北京:化学工业出版社，1994.73-84.

[12]冯兴奎，杨红.带纵向加强筋外压圆筒的稳定性研究[J].压力容器，2000，17（1）:9-12.

StructuralDesign ofBuried Tank and NumericalSimulation byANSY SSoftware

Yu Rangang，Liu Hao，Song Longjie，Zhu Xiaoxiao，Nong Yi，Zhu Hai
College of Pipeline and CivilEngineering，China University of Petroleum，Qingdao 266580，China

In this paper,the structural design methods for buried tank are summarized,the stress characteristics are analyzed, and the numerical simulation method by ANSYS software is proposed according to special working conditions of the tank.In view of a specific tank design instance,the numerical model is established and the deformation and stress of the tank are calculated by ANSYS software after the structural design done.Comparative analyses on the theoretical calculation results and the numerical simulation results are conducted to verify the correctness of the numerical simulation results，and the unreasonable points in traditional stability design are pointed out,which prove the importance of the numericalsimulation as reference and supplement for structuraldesign of buried tank.

buried tank；structuraldesign；ANSYS；numericalsimulation；deformation；stress

10.3969/j.issn.1001-2206.2014.06.001

俞然刚（1967-），男，山东德州人，教授，2008年获中国石油大学（华东）博士学位，主要从事地应力、储罐、材料性能及测试等方面的教学与科研工作。

2014-03-03