基于多尺度模型修正的结合梁斜拉桥损伤识别方法

钟儒勉 宗周红 秦中远 郑沛娟

(东南大学土木工程学院，南京210096)

20世纪80年代以来，众多km级大跨径桥梁不断刷新着桥梁建设的各项记录，然而大尺度桥梁往往伴随着cm乃至mm级的微小损伤，即产生了结构损伤的多尺度问题.目前，Barenblatt等[1－3]探讨了结构多尺度的数学理论模型，将力学的宏观方程与微观方程转变为动力学方程，并实现了联立求解，提出了表征微结构的特征与宏观特征关系的无量纲数——Deborah数，全面分析了结构失效中的尺度效应及其物理来源.白以龙等[4-6]展开了多尺度物理模型的研究，提出在结构受力较复杂的、易损的部位建立精细小尺度模型，并与整体大尺度结构耦合形成同一结构不同尺度下的模型，即多尺度模型.在此基础上，Ladeveze等[7-9]进一步探讨了多尺度模拟中关键的尺度耦合效应，为研究结构损伤破坏提供了条件.在结构的损伤识别方面，传统的单一尺度损伤识别较为广泛[10-12]，并提出了基于静动力指纹的方法[13-15]、基于模型修正的方法[16-18]、基于实测时域信号的方法[19]以及基于神经网络的方法[20]等，然而单一尺度下很难达到结构损伤识别的目标，因此，展开多尺度模型下的结构损伤识别研究成为了一种损伤识别的新思路.

多尺度模型要尽可能精确地反应结构的实际状态，这是多尺度模型修正的目的[21-22].本文以灌河大桥结合梁斜拉桥为工程背景，研究了基于多尺度模型修正的损伤识别方法.首先建立了该结合梁斜拉桥的多尺度有限元模型，并基于现场环境振动试验结果和两阶段响应面方法对初始多尺度模型进行修正，并将修正后的多尺度模型作为未损基准模型;进而选取模态曲率和模态应变能损伤指标，分别探讨基于模型修正的方法对采用精细小尺度单元建立的中跨跨中区域和大尺度单元建立的边跨跨中区域进行损伤识别的有效性;最后分析了小尺度区域和大尺度区域在损伤识别过程中的噪声鲁棒性.

1 结构损伤定位指标

结构的局部损伤通常表现为某一部位的刚度降低，这必然会导致结构动力特性的改变，即结构固有频率和固有振型的改变.其中，模态曲率和单元模态应变能为结构的固有动力特性指标，从机理上能够有效识别出损伤位置和损伤程度.

1.1 模态曲率指标

对于第j阶模态，模态曲率指标C定义为[23]

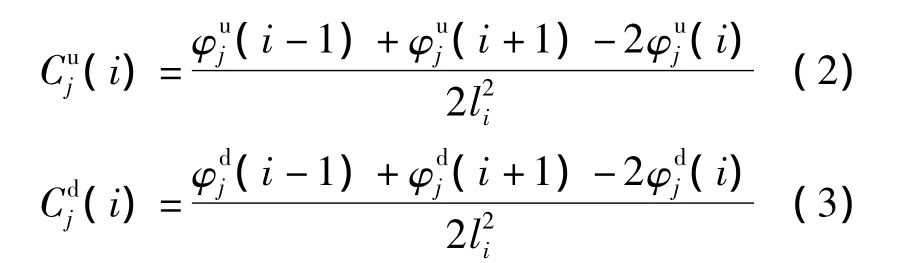
1.2 单元模态应变能指标

以梁结构为例，第j号单元在损伤前后第i阶模态下的单元模态应变能分别为[23-24]

式中，Eij，E'ij分别为结构损伤前后第 j号单元第 i阶模态应变能;(EI)j，(EI)'j为损伤前后第j号单元刚度;φ″i(x)，(φ″i(x))'分别为损伤前后第 i阶模态振型.故可定义第j号单元在第i阶模态下的损伤指标为

为了充分探讨各损伤指标的敏感性，本文分别计算前3阶模态曲率指标、单元模态应变能指标，并定义结构第j号单元损伤总指标为前3阶损伤指标的代数平均值.

2 基于两阶段多尺度模型修正的损伤识别方法

两阶段响应面模型修正是指将响应面方法分别应用于多尺度建模修正和模型参数修正参数中，旨在将多尺度建模误差(多尺度模型与精确有限元模型之间的误差)与模型参数误差(初步修正后多尺度模型与实际结构之间的误差)区分开来而不至于失去模型修正的物理意义.利用两阶段响应面方法可得到实际结构损伤前的有效多尺度模型，该模型已消除多尺度建模误差，在此基础上进行一般响应面模型修正即可得到损伤后的有效多尺度模型，由损伤前后的多尺度模型分别计算出结构的模态曲率和模态应变能，进而得到结构损伤指标，即可确定结构损伤位置和损伤程度.引入了两阶段响应面模型修正技术的多尺度损伤识别方法流程如图1所示.

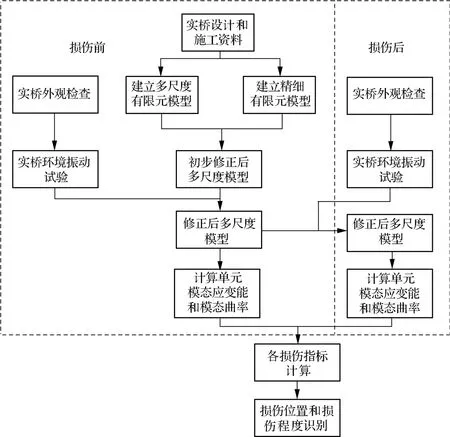
图1 基于两阶段响应面模型修正的多尺度损伤识别流程图

3 灌河大桥多尺度模型及其两阶段模型修正

灌河大桥主桥采用双塔双索面半飘浮5跨连续组合梁斜拉桥，主桥布置及其多尺度模型如图2所示，跨径组成为(32.9+115.4+340.0+115.4+32.9)m.其中A1区域为精细小尺度实体单元(cm级尺度);A2为粗糙大尺度梁单元(m级尺度).基于全桥环境振动试验结果，引入两阶段响应面模型修正方法，以竖向三阶、横向二阶、纵向一阶和扭转一阶共7个参数为响应值，选取包括主梁刚度、边界条件、混凝土弹性模量在内的7个待修正参数(见表1)，对灌河大桥主桥多尺度有限元模型进行修正.结果表明[22]，经过两阶段响应面模型修正后的计算结果与实测结果吻合较好，最大频率相对误差不超过8%，表征模态保证准则的MAC值基本在90%以上，如表2所示.

4 灌河大桥主梁损伤识别

本文采用修正后的灌河大桥有限元模型来模拟该桥主梁损伤.分别选取小尺度A1区域和大尺度A2区域模拟灌河大桥主梁损伤工况，具体如下:

图2 灌河大桥

表1 灌河大桥两阶段模型修正参数选取及修正后值

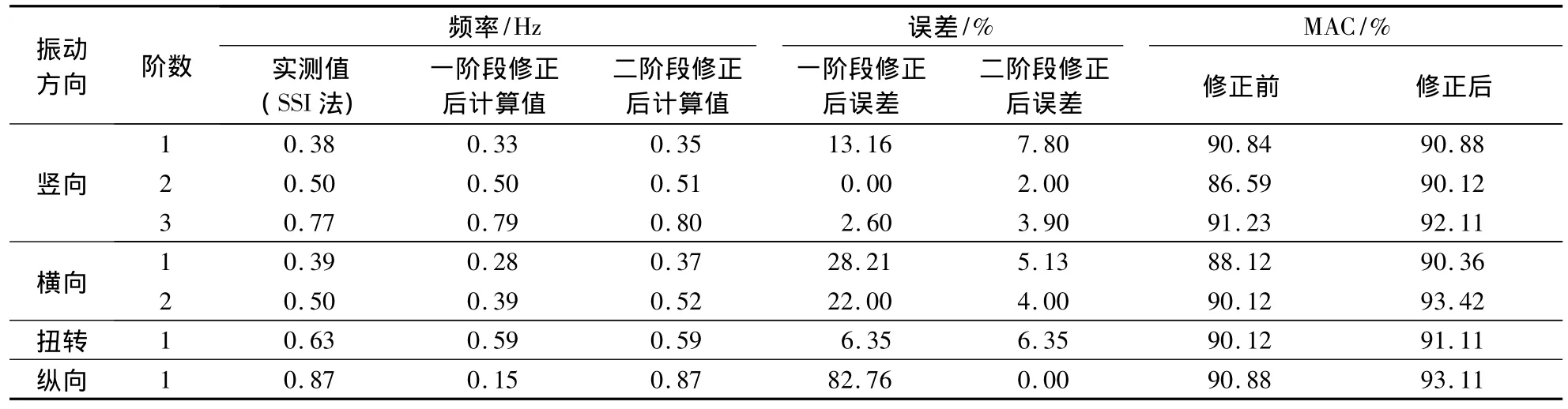
表2 修正后频率与实测频率的比较

1)工况1 小尺度A1区域主梁刚度降低5%.

2)工况2 小尺度A1区域主梁刚度降低3%.

3)工况3 小尺度A1区域主梁刚度降低1%.

同学们，如果你也喜欢汉服，就来“最美汉服秀”晒一晒你身着汉服的美照吧，说不定下一期杂志上就会出现你的身影哦。

4)工况4 大尺度A2区域主梁刚度降低5%.

5)工况5 大尺度A2区域主梁刚度降低3%.

6)工况6 大尺度A2区域主梁刚度降低1%.

7)工况7 大尺度A2及小尺度A1区域主梁刚度均降低1%.

4.1 损伤敏感性分析

将灌河大桥多尺度模型在模拟结构受损后计算得到的频率代入响应面模型，得到修正参数(见表3)，进而建立灌河大桥主梁不同损伤后的有限元模型.

基于主梁不同损伤后的灌河大桥有限元模型，利用式(1)～(7)计算各工况下的损伤指标，以工况3和工况7为例，其结果如图3和图4所示.

在不考虑噪声干扰的情况下，由图3和图4可知:①对于结合梁斜拉桥，当主梁小尺度区域损伤程度在5%，3%及1%时，模态曲率和模态应变能指标在损伤部位的变化率较大，而未损伤部位变化率接近于0.②当主梁大尺度和小尺度区域损伤程度均为1%时，模态曲率和模态应变能在小尺度损伤部位的变化率较大，而大尺度损伤部位的变化率较小尺度部位略小.③ 模态曲率和模态应变能总指标在大尺度损伤部位和小尺度损伤部位均存在程度不同但较为明显的变化，且模态应变能较模态曲率的变化率略明显.

表3 实际参数值与修正后参数值比较

4.2 噪声鲁棒性分析

式中，f和f0分别为加噪前后的频率值或振型分量;ε为噪声水平;R为[－1，+1]内服从正态分布的白噪声信号.

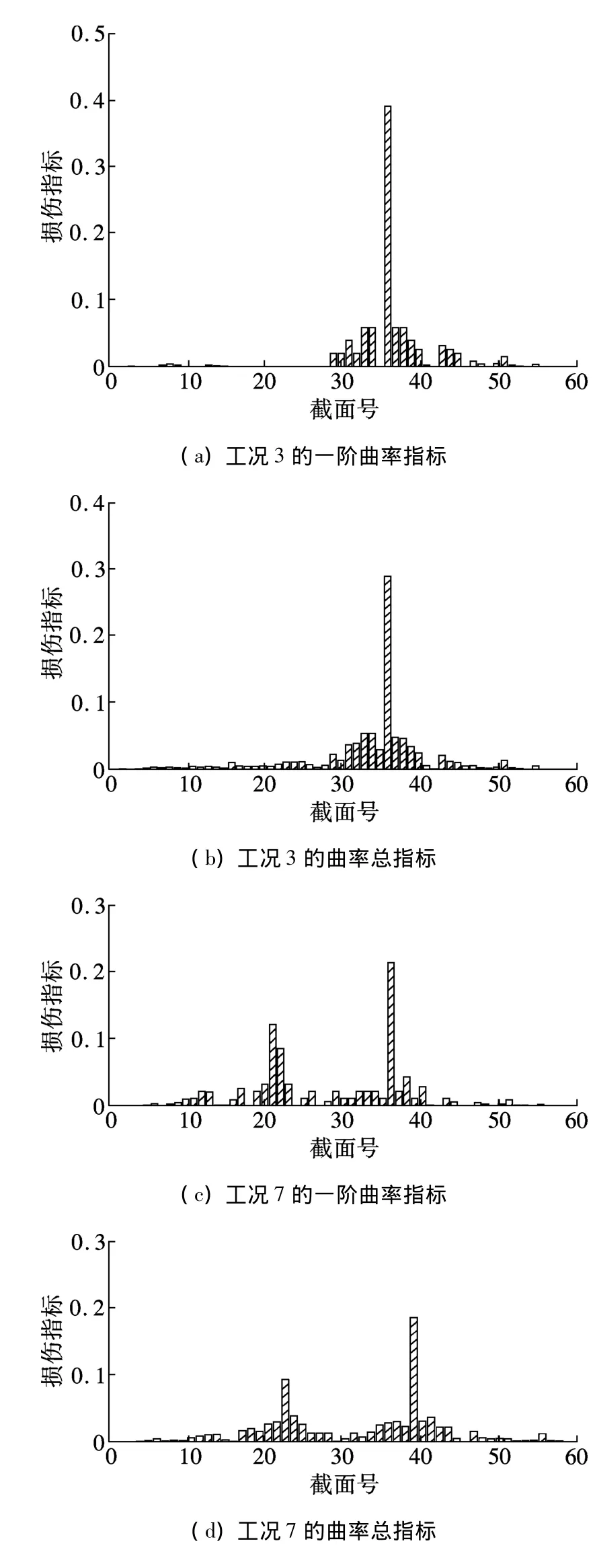
图3 模态曲率指标计算结果

分别考虑1%，3%，5%的噪声干扰，利用式(1)～(7)计算在损伤工况7下模态曲率和模态应变总指标，结果如图5所示.

在考虑1%，3%，5%噪声干扰的情况下，由图5可知:①随着噪声水平的增加，模态曲率和模态应变能总指标对于损伤的敏感性降低.②中跨跨中小尺度模型区域损伤识别的抗噪性更好，在5%噪声干扰下，各损伤指标基本能识别出跨中小尺度的损伤工况;而跨中大尺度单元区域损伤识别的抗噪性较差，在5%噪声干扰下，基本失去微损伤识别能力.③在多尺度损伤识别过程中，模态应变能损伤指标的抗噪性要略优于模态曲率损伤指标.

图4 模态应变能指标计算结果

图5 损伤指标计算结果

5 结论

1)在不考虑噪声干扰的情况下，模态曲率和模态应变能指标对斜拉桥结构小尺度微损伤均较为敏感，结合响应面模型修正方法，可以识别出损伤的位置，而斜拉桥结构大尺度损伤敏感性较小尺度区域略低，模态应变能总指标均能取得较好的损伤识别效果.

2)在考虑噪声干扰的情况下，小尺度单元区域比大尺度单元区域的损伤识别抗噪性更好，对结构5%噪声干扰基本能够识别，且模态应变能损伤指标的抗噪性要略优于模态曲率损伤指标.

3)本文提出的基于多尺度模型修正的结合梁斜拉桥损伤识别主要基于两阶段响应面模型修正方法展开，其精细小尺度区域对微损伤的高敏感性和抗噪性使其可以较好地应用于结构损伤识别中，并为基于健康监测的安全评估和损伤预后奠定了基础.

References)

[1] Barenblatt G I.Micromechanics of fracture[C]//Theoretical and Applied Mechanics.Amsterdam:Elsevier Science Publishers，1992:25-52.

[2] Bazant Z P，Chen E P.Scaling of structural failure[J].Appl Mech Rev，1997，50(10):593-627.

[3] Glimm J，Sharp D H.Multiscale science:a challenge for the twenty-first century [J].Advances in Mechanics，1998，28(4):545-551.

[4] 白以龙.工程结构损伤的两个重要科学问题——分布式损伤和尺度效应[J].华南理工大学学报，2002，30(11):11-14.Bai Yilong.Two important scientific problems in engineering structures—distributed damages and scale effect[J].Journal of South China University of Technology:Natural Science Edition，2002，30(11):11-14.(in Chinese)

[5] Li Z X，Zhou T Q，Chan T H T，et al.Multi-scale numerical analysis on dynamic response and local damage in long-span bridges[J].Engineering Structures，2007，29(7):1507-1524.

[6] Li Z X，Jiang F F，Tang Y Q.Multi-scale analyses on seismic damage and progressive failure of steel structures[J].Finite Elements in Analysis and Design，2012，48(1):1358-1369.

[7] Ladeveze P，Nouy A.On a multiscale computational strategy with time and space homogenization for structural mechanics[J].Computer Methods in Applied Mechanics and Engineering，2003，192(28/29/30):3061-3087.

[8] Takizawa K，Tezduyar T E.Multiscale space-time fluidstructure interaction techniques[J].Computational Mechanics，2011，48(3):247-267.

[9] Liu W K，Dong Q，Stefano G，et al.Multiscale methods for mechanical science of complex materials:bridging from quantum to stochastic multi-resolution continuum[J].International Journal for Numerical Methods in Engineering，2010，83(8/9):1039-1080.

[10] 宗周红，牛杰，王浩.基于模型确认的结构概率损伤识别方法研究进展[J].土木工程学报，2012，45(8):121-130.Zong Zhouhong，Niu Jie，Wang Hao.A review of structural damage identification methods based on the finite element model validation[J].China Civil Engineering Journal，2012，45(8):121-130.(in Chinese)

[11] Marwala T.Finite-element-model updating using computational intelligence techniques—applications to structural dynamic[M].London:Springer，2010:1-15.

[12] Oberkampf W L，Roy C J.Verification and validation in scientific computation[M]. London:Cambridge University Press，2010:1-19.

[13] Adams R D，Cawley P，Pye C J，et al.Vibration technique for non-destructively assessing integrity of structures[J].Journal of Mechanical Engineering Science，1978，20(2):93-100.

[14] Dong C，Zhang P Q，Feng W Q，et al.The sensitivity study of the modal parameters of a cracked beam[C]//Proceedings of the 12th International Modal Analysis Conference.Hawaii，USA，1994:98-104.

[15] Lim T W.Structural damage detection using modal test data[J].AIAA Journal，1991，29(12):2271-2274.

[16] Fang S E，Perera R.Damage identification by response surface based model updating using D-optimal design[J].Mechanical Systems and Signal Processing，2011，25(2):17-33.

[17] Zimmerman D C，Kaouk M.Structural damage detection using a minimum rank updates theory[J].Journal of Vibration and Acoustics，Transactions of the ASME，1994，116(2):222-231.

[18] Ren W X，Fang S E，Deng M Y.Response surfacebased finite-element-model updating using structural static responses[J].Journal of Engineering Mechanics，2011，137(4):248-257.

[19] Gangone M V，Whelan M J，Janoyan K D.Wireless monitoring of a multi-span bridge super structure for diagnostic load testing and system identification[J].Computer-Aided Civil and Infrastructure Engineering，2011，26(7):569-579.

[20] Elkordy M F，Chang K C，Lee G C.Application of neural networks in vibration signature analysis[J].Journal of Engineering Mechanics，1994，120(2):250-265.

[21] 钟儒勉，樊星辰，黄学漾，等.基于两阶段响应面方法的结合梁斜拉桥多尺度有限元模型修正[J].东南大学学报:自然科学版，2013，43(5):993-999.Zhong Rumian，Fan Xingchen，Huang Xueyang，et al.Multi-scale finite element model updating of composite cable-stayed bridge based on the two-phase response surface methods[J].Journal of Southeast University:Natural Science Edition，2013，43(5):993-999.(in Chinese)

[22] 丁幼亮，李爱群，缪长青.大跨斜拉桥扁平钢箱梁的多尺度损伤分析研究[J].工程力学，2009，11(6):60-66.Ding Youliang，Li Aiqun，Miao Changqing.Multi-scale damage analysis for steel box girder of long-span cablestayed bridges[J].Engineering Mechanics，2009，11(6):60-66.(in Chinese)

[23] 宗周红，褚福鹏，牛杰.基于响应面模型修正的桥梁结构损伤识别方法[J].土木工程学报，2013，46(2):115-122.Zong Zhouhong，Chu Fupeng，Niu Jie.Damage identification methods of bridge structures using response surface based on finite element model updating[J].China Civil Engineering Journal，2013，46(2):115-122.(in Chinese)

[24] 宗周红，任伟新.桥梁有限元模型修正与模型确认[M].北京:人民交通出版社，2012:135-168.