Design formulas of transmission coefficients for permeable breakwaters
Su-xiang ZHANG, Xi LI*
1. Key Laboratory of Meteorological Disaster of Ministry of Education, Nanjing University of Information Science and Technology, Nanjing 210044, P. R. China
2. Department of Civil Engineering and Applied Mechanics, McGill University, Montreal, Quebec H3A 2K6, Canada
3. College of Harbor, Coastal and Offshore Engineering, Hohai University, Nanjing 210098, P. R. China
Design formulas of transmission coefficients for permeable breakwaters
Su-xiang ZHANG1,2, Xi LI*3
1. Key Laboratory of Meteorological Disaster of Ministry of Education, Nanjing University of Information Science and Technology, Nanjing 210044, P. R. China
2. Department of Civil Engineering and Applied Mechanics, McGill University, Montreal, Quebec H3A 2K6, Canada
3. College of Harbor, Coastal and Offshore Engineering, Hohai University, Nanjing 210098, P. R. China
New empirical formulas of the transmission coefficient for permeable breakwaters were suggested based on available experimental data regarding the low-crest structure (LCS), including the permeable rubble mound breakwater and pile-type breakwater. The rationality of the present formulas was verified by their comparison with existing empirical and analytical formulas. Numerical flume results were obtained by solving the modified Boussinessq-type wave equations (MBEs), and a new expression relating the friction coefficient α to the relative submerged depth RtHswas also derived. Comparative analysis shows that the results of the present formulas agree with the numerical flume results as well as available experimental data, and the present formulas are superior to the existing empirical and analytical expressions in estimating the transmission coefficient. The present formulas can provide references for estimation of the transmission coefficient in engineering practice.
permeable breakwater; transmission coefficient; wave reflection; nonlinear wave; Boussinesq wave model; low-crest structure
1 Introduction
The main characteristic of a wave-permeable breakwater is that a wave can move through the breakwater without changing its profile, while wave diffraction is not dependent on whether the structure is permeable or not. Wave overtopping and transmission are the main modes of energy transportation for waves moving through the permeable breakwater, with some energy dissipated by wave breaking on the seaward side or by turbulence inside the breakwater, and some energy reflected in front of the structure. Thus, a detailed description of nearshore hydrodynamics is of engineering value in examining wave and structure interaction. Although the nonlinear wave theory has been widely developed, it is still difficult to apply it directly to engineering design because of the inconvenience in estimating the transmission coefficient. Linear theories and empirical equations have a practical advantage in analysis ofwave transformation, including an overall description of phenomena like wave breaking, run-up, and overtopping. Permeable breakwaters, especially the pile type, have been widely used in coastal protection, wave reduction, and ship berthing. It is useful for engineering design to predict the transmitted wave height and transmission coefficient with a simple and convenient empirical formula. In this study, the transmission coefficient of permeable breakwaters was analyzed based on available experimental data regarding the low-crest structure (LCS) (van der Meer et al. 2005; Chen et al. 2008; Li and Xie 2008; Peng et al. 2009), including an emergent porous rubble mound breakwater and a pile-type breakwater. Based on available data (Madsen 1983; Luth et al. 1994; Christou et al. 2008; van der Meer et al. 2005), two other permeable structures were also investigated: a porous rubble mound breakwater before a rigid wall and a submerged breakwater. For the purpose of design convenience, new empirical formulas of the transmission coefficient were suggested, and the rationality was verified by their comparison with existing formulas, e.g., the analytical formula of Wiegel (1961) and the empirical formulas of van der Meer and Daemen (1994) and d’Angremond et al. (1996). Then, numerical flume results obtained by solving the modified Boussinesq-type wave equations (MBEs) for pile-type breakwaters were analyzed and compared with the results of the present empirical formula and the analytical formula of Wiegel (1961), as well as physical model data (Madsen 1991; Li and Yan 2005; Fuhrman and Madsen 2008).
2 Existing analytical and empirical formulas for transmission coefficients and present formulas
The transmission coefficient is directly related to the type of wave-permeable structures. The two types primarily examined in this investigation were the emergent porous rubble mound type (Fig. 1(a)) and pile type (Fig. 1(b)).

Fig. 1 Permeable breakwaters
For a rubble mound breakwater, based on extensive experimental data, van der Meer and Daemen (1994) suggested the following expression using the medium diameter of breakwater body stones to describe the transmission coefficient:

where Ktis the transmission coefficient, with Kt=HkHs; Hkis the height of the transmitted wave behind the permeable breakwater; Hsis the significant wave height of the incident wave; Rcis the crest freeboard; Dn50is the medium diameter; a and b are parameters, with a =0.031HsDn50− 0.024, and b =− 5.42 Sop+ 0.0323HsDn50− 0.017 (B Dn50)1.84+ 0.51; Sopis the wave steepness, withis the peak period of the incident wave; g is the gravitational acceleration; and B is the upper structure width.
d’Angremond et al. (1996) related the transmission coefficient to RcHs, BHs, and breaker parameter ζop:

where the breaker parameter or the Iribarren number ζop=hx(Sop)12, and hxis the seaward slope of the structure.
For the rubble mound breakwater, laboratory test results are available from various studies (Kramer et al. 2005; Calabrese et al. 2008; Peng et al. 2009; Hur et al. 2012; Melito and Melby 2002; Laju et al. 2011). They were compared with the two formulas above in terms of function design of the crest freeboard Rcand upper structure width B. As a result, Eq. (1) can be applied to the rubble mound breakwater; Eq. (2) is not limited to the rubble mound breakwater, but a large deviation may occur when it is applied to other types of permeable breakwaters, especially those with a large transmission coefficient.
Based on the small amplitude wave theory, the analytical solution of linear waves across a thin vertical pile interface was suggested by Wiegel (1961). The expression based on the linear theory neglects the nonlinear damping effect, and thus the equation provides a larger transmission coefficient:

where the adjustment coefficient η is less than 1, and, usually, η=0.9 according to a simple correlation analysis considering energy dissipation; k is the wave number; d is the still water depth; and Rtis the submerged depth of a splashing board of pile-type breakwaters.
The present investigation was performed based on available data and above analytical and empirical formulas. For the rubble mound breakwater, the crest freeboard Rcplays an important role in evaluating transmission effects, which is crucial in determining wave transmission, reflection, and overtopping, and has a linear relation with Ktin Eq. (2).
Considering this factor, a better way to correlate Rcwith Ktusing a shape function is
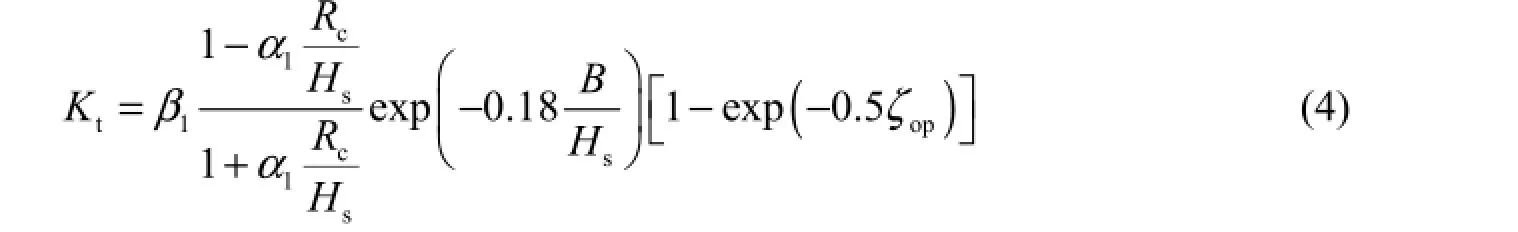
where α1(here α1RcHs≤ 1.0) and β1are two coefficients for the rubble mound breakwater. Since RcHsis usually closeto 1 in practice, with reference to the Code of Design and Construction of Breakwaters (MT PRC 2011), we determined that α1= 1.0 and β1= 0.90 by fitting the laboratory data from van der Meer et al. (2005) and conducting a simple correlation analysis, as shown in Fig. (2).

Fig. 2 Determination of α1and β1for emergent porous rubble mound breakwater by fitting data extracted from van der Meer et al. (2005)
For the pile-type permeable breakwater, the submerged depth of the splashing board Rtplays an important role in defining the transmission coefficient Kt. Replacing α1RcHsin Eq. (4) with α2RtHs, the following empirical formula is introduced:

where α2and β2are two coefficients for the pile-type breakwater, which were determined to be 0.23 and 2.3, respectively, through analysis of the experimental data (Li and Yan 2005) provided in the next section.
The submerged breakwater (Fig. 1(d)) is more similar to the pile-type breakwater than to the rubble mound breakwater in wave transmission effects, since both the pile type and the submerged type have a continuous water body. As shown in Fig. 3,2α and2β were determined to be 0.23 and 0.50, respectively, in Eq. (5) for the submerged breakwater, based on fitting of the laboratory data from van der Meer et al. (2005) and a simple correlation analysis.
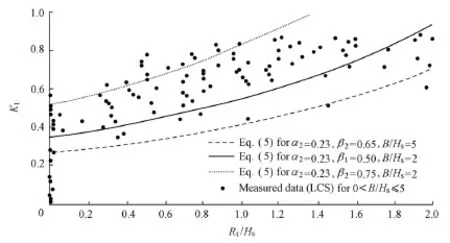
Fig. 3 Determination of α2and β2for submerged breakwater by fitting data extracted from van der Meer et al. (2005)
3 Comparison of present and existing empirical formulas of transmission coefficients
Based on 2337 LCS data sets from van der Meer et al. (2005) and Zanuttigh et al. (2008), Eq. (4) was compared with Eq. (2).As shown in Fig. 4(a), Eq. (4) has a wider range of application, especially for BHs>1 0. Fig.4(b) indicates that the transmission coefficient Ktdecreases exponentially with the increment of RcHsaccording to Eq. (4), which is more consistent with the measured data than the linear relation in Eq. (2).

Fig. 4 Comparison of calculated results of Eq. (2) and Eq. (4) for rubble mound breakwater
As described by Fig. 5, for a pile-type breakwater, the calculated results of Eq. (3) show larger values of the transmission coefficient Ktthan the results of Eq. (5) and laboratory data from Li and Yan (2005), because Eq. (3) does not consider energy dissipation by LCS. We determined that α2= 0.23 and β2=2.3 in Eq. (5) based on a simple correlation analysis. Fig. 5 shows that the calculated results ofEq. (5) are closer to the laboratory data from Li and Yan (2005). For larger values of relative submerged depth RtHs(i.e., smaller values of RcHs), overtopping less than 0.2Hsmay occur in the laboratory data, while, for smaller values of RtHs(i.e., larger values of RcHs), experimental data from Li and Yan (2005)show no overtopping effects. It is suggested that the overtopping effects for larger values of RtHsmay be considered by slightly increasing the value of coefficient β2in Eq. (5). In conclusion, Eq. (5) shows an acceptable accuracy in comparison with experimental data and can be used for estimating the transmission coefficient for pile-type breakwaters.
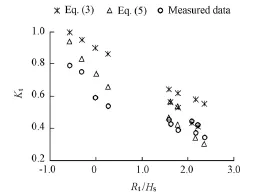
Fig. 5 Comparison of experimental data (Li and Yan 2005) and calculated results of Eq. (3) and Eq. (5) for pile-type breakwater
4 Numerical flume tests based on MBE model and verification of present empirical formula for pile-type breakwater
4.1 MBE model
In the numerical flume, the friction term of the porosity expression was added to governing equations to modify the classic Boussinesq-type wave equations (Madsen 1983). The nonlinear friction term inside the permeable structure (or the porous absorber) in shallow water can be linearized by using the following approximation:

where Uis the velocity vector; αand β are the friction coefficients of permeable structures accounting for the laminar and turbulent friction losses, respectively; f is the friction factor independent of time t and space in x and y dimensions; ω is the incident wave angular frequency; and n is the porosity coefficient of structures. α and β are related to the porosity coefficient n from Engelund (1953):

where υ is the kinetic viscosity, and α0and β0are constants.
The expression on the right-hand side of Eq. (6) (Madsen 1983) was derived under one-dimensional shallow-water long-wave conditions by neglecting higher order nonlinear effects. Considering that this assumption causes uncertainty in understanding short wavetransmission, the items on the left-hand side of Eq. (6) are directly applied to MBE by setting β as a constant in numerical flume tests and α at a value less than 10. Eqs. (7) and (8) demonstrate the porosity effects on the hydrodynamic characteristic of permeable breakwaters by assuming a nominal Dn50value.
Since the MBE model is based on the depth-averaged two-dimensional water flow, the corresponding mathematical formulation of permeable structures is similar to that used to solve the problem of waves passing through permeable screens, where the transmitted and reflected waves occur on both sides of the screen. In the numerical flume, the transmission coefficient can be determined by the friction factor α and the number of friction layers (Li and Yan 2005; Zhang and Li 2008). Different types of permeable structures, as shown in Fig. 1, were tested with the MBE model in this study.
4.2 Comparison of numerical flume results with physical model data
The wave attenuation effects were tested for four specific types of permeable breakwaters using the MBE model. The instant wave elevation distribution and wave height distribution for waves moving through different types of permeable breakwaters are illustrated in Fig. 6 and Fig. 7. A typical standing wave and a transmitted propagating wave form respectively in front of and behind thepermeable structures for all types of breakwaters except for the porous breakwater before a rigid wall. The numerical flume results using the MBE model and physical model data for different types of permeable breakwaters are listed in Table 1, where Kr=HrHs, with Hrindicating the reflected wave height in front of the breakwater. It can be concluded that the numerical flume results agree with the physical model data.
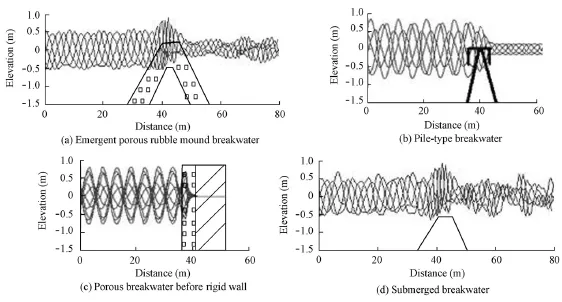
Fig. 6 Wave envelopes in numerical flume

Fig. 7 Wave height distributions in numerical flume
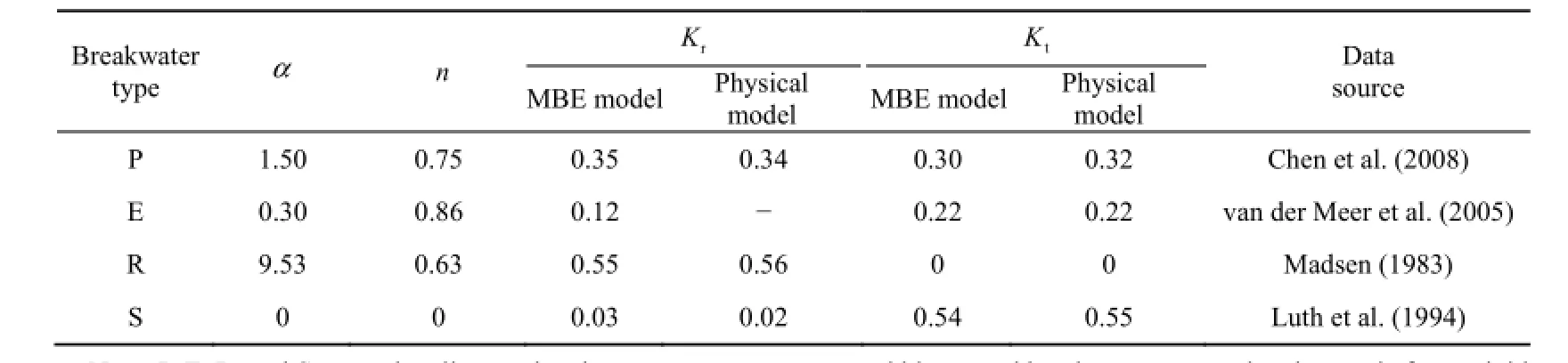
Table 1 Comparison of numerical flume results using MBE model with physical model data for different types of permeable breakwaters
4.3 Comparisons of numerical flume results with physical model data and results of analytical and empirical formulas for pile-type breakwater
Numerical flume tests on the pile-type breakwater were performed using the MBE model. The data sets from P01 to P12 for the numerical flume are listed in Table 2, where BHsis determined to be 5 in accordance with the physical model tests (Chen et al. 2008).

Table 2 Data sets for numerical flume tests
The numerical flume results were compared with the calculated results of Eq. (5) and Eq. (3) as well as the physical model data from Chen et al. (2008), as shown in Fig. 8. A decaying trend of Ktis demonstrate d with the increment of RtHs, and the empirical curve of Eq. (5) agrees with the numerical flume results and the measured data. In general, the overtopping effects of the pile-type breakwater will lead to an increase of Kt. This is outside of the scope of the present investigation since these effects only occur in physical models. By fitting the data of α and RtHsin Table 2, as shown in Fig. 9, a new empirical relationrelating α to RtHswas obtained as follows:

Comparisons of the transmission coefficient Ktobtained by the MBE model with those obtained by the formulas (Eq. (3) and Eq. (5)) and the physical model against the friction coefficient α and the porosity coefficient n, with the friction coefficient α obtained by Eq. (9), are shown in Fig. 10. The agreement between the results of the MBE model, the physical model, and Eq. (5) demonstrates that Eq. (9) has a strong fitting effect, and the numerical flume has a wide range of applicability. The results also show that Eq. (5) is superior to Eq. (3) in estimating the transmission coefficient for pile-type breakwaters.

Fig. 8 Comparisons ofKtagainstR t H s
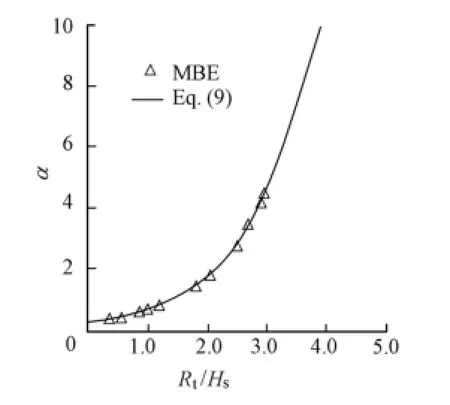
Fig. 9 α versusR t Hs

Fig. 10 Comparisons ofKtagainstαand n .
4.4 Discussion
In coastal engineering practice, RtHsmay exceed 2 for many reasons, such as reduction of the transmission coefficient Ktby increasing reflection and regulating tidal levels. In addition, damping effec ts of BHsplay an important role in breaking waves, which means that a close relationship exists between Ktand BHs: as RtHs→0 in Eq. (9), α→0.23, and, accordingly, Kt→ 2.3exp (− 0.18BHs)in Eq. (5). Considering that viscosity and nonlinearity are of great significance in the determination of BHs, especiallyfor three-dimensional shallow water, further verification and improvement regarding the nonlinearity should be focused on the relationship between BHsand the coefficient β in Eq. (6) in the future. Although numerical simulation tests are becoming more valuable with the development of computer capability and calculation speed, the MBE model can only be successfully applied to two-dimensional simulations, and three-dimensional simulations of wave phenomena are still difficult. Thus, physical models still play an important role in understanding basic mechanics of wave phenomena.
5 Conclusions
Based on the analysis of existing analytical and empirical formulas for the transmission coefficient of permeable breakwaters, new empirical formulas were developed, with their coefficients obtained by fitting laboratory data. These formulas were verified through comparison with numerical flume tests and physical model tests. It can be concluded that the present formula for rubble mound-type breakwaters has a wider application range than the existing empiricalformulas, and that the results of the present formula for pile-type breakwaters are more consistent with both the numerical flume results and the physical model data than those of the existing analytical formula. Moreover, an empirical formula relating the friction coefficient α to the relative submerged depth RtHswas also derived and verified, in which α is a vital factor in wave transmission simulation with the MBE model.
Calabrese, M., Buccino, M., and Pasanisi, F. 2008. Wave breaking macrofeatures on a submerged rubble mound breakwater. Journal of Hydro-environment Research, 1(3-4), 216-225. [doi:10.1016/10.1016/ j.jher.2007. 11.003]
Chen, D. C., Wang, Y. G., Li, X., Yang, Y., and Cai, H. 2008. Experimental Study of Wave Permeable Breakwater in Sansha Central Fishing Port. Nanjing: Hohai University. (In Chinese)
Christou, M., Swan, C., and Gudmestad, O. T. 2008. The interaction of surface water waves with submerged breakwaters. Coastal Engineering, 55(12), 945-958. [doi:10.1016/j.coastaleng.2008.02.014]
d’Angremond, K., van der Meer, J. W., and de Jong, R. J. 1996. Wave transmission at low crested structures. Proceedings of the 25th International Conference on Coastal Engineering, 2418-2427. Florida: ASCE.
Engelund, F. 1953. On the laminar and turbulent flows of ground water through homogeneous sand. Transactions of Danish Academy Technical Science, Vol. 3.
Fuhrman, D. R., and Madsen, P. A. 2008. Simulation of nonlinear wave runup with a high-order Boussinesq model. Coastal Engineering, 55(2), 139-154. [doi:10.1016/j.coastaleng.2007.09.006]
Hur, D. S., Lee, W. D., and Cho, W. C. 2012. Characteristics of wave run-up height on a sandy beach behind dual-submerged breakwaters. Ocean Engineering, 45, 38-55. [doi:10.1016/j.oceaneng.2012.01.030]
Kramer, M., Zanuttigh, B., van der Meer, J. W., Vidal, C., and Gironella, F. X. 2005. Laboratory Experiments on low-crested breakwaters. Coastal Engineering, 52(10-11), 867-885. [doi:10.1016/j.coastaleng. 2005.09.002]
Laju, K., Sundar, V., and Sundaravadivelu, R. 2011. Hydrodynamic characteristics of pile supported skirt breakwater models. Applied Ocean Research, 33(1), 12-22. [doi:10.1016/j.apor.2010.12.004]
Li, C. L., and Xie, Y. Y. 2008. Random wave motions around different submerged dikes. Coastal Engineering, 27(1), 1-9. (in Chinese)
Li, X., and Yan, Y. X. 2005. Numerical simulations of nonlinear wave transformation around wave-permeablestructure. Journal of Hydrodynamics, Ser. B, 17(17), 699-703.
Luth, H. R., Klopman, Q., and Kitou, N. 1994. Kinematics of Waves Breaking Partially on an Offshore Bar. Delft: Delft Hydraulics.
Madsen, P. A. 1983. Wave reflection from a vertical permeable wave absorber. Coastal Engineering, 7(4), 381-396. [doi:10.1016/0378-3839(83)90005-4]
Madsen, P. A. 1991. A new form of the Boussinesq equations with improved linear dispersion characteristics. Coastal Engineering, 15(4), 371-388. [doi:10.1016/0378-3839(92)90019-Q]
Melito, I., and Melby, J. A. 2002. Wave runup, transmission, and reflection for structures armored with CORE-LOC. Coastal Engineering, 45(1), 33-52. [doi:10.1016/S0378-3839(01)00044-8]
Ministry of Transport of People’s Republic of China (MT PRC). 2011. Code of Design and Construction of Breakwaters (JTS 154-1-2011). Beijing: China Communications Press. (in Chinese)
Peng, Z., Zou, Q., Reeve, D. E., and Wang, P. X. 2009. Parameterisation and transformation of wave asymmetries over a low-crested breakwater. Coastal Engineering, 56(11-12), 1123-1132. [doi:10.1016/ j.coastaleng.2009.08.005]
van der Meer, J. W., Briganti, R., Zanuttigh, B., and Wang, B. X. 2005. Wave transmission and reflection at low-crested structures: Design formulae, oblique wave attack and spectral change. Coastal Engineering 52(10-11), 915-929. [doi:10.1016/j.coastaleng.2005.09.005]
van der Meer, J. W., and Daemen, I. F. R. 1994. Stability and wave transmission at low crested rubble mound structures. Journal of Waterway, Port Coastal and Ocean Engineering, 120(1), 1-9. [doi:10.1061/(ASCE) 0733-950X(1994)120:1(1)]
Wiegel, R. L. 1961. Closely spaced piles as a breakwater. Dock and Harbor Authority, 42(491), 150.
Zanuttigh, B., Martinelli, L., and Lamberti, A. 2008. Wave overtopping and piling-up at permeable low crested structures. Coastal Engineering, 55(6), 484-498. [doi:10.1016/j.coastaleng.2008.01.004]
Zhang, S. X., and Li, X. 2008. Numerical simulation of nonlinear wave propagating in flume. Proceedings of Fourth International Conference on Natural Computation, 649-653. Perth: IEEE. [doi:10.1109/ICNC. 2008.854]
(Edited by Ye SHI)
This work was supported by the Key Project in the National Science and Technology Pillar Program for the Twelfth Five-Year Plan Period (Grant No. 2012BAB03B01), and the Jiangsu Provincial Post-Doctoral Support Plan (Grant No. 20100197).
*Corresponding author (e-mail: xili@hhu.edu.cn)
Received Feb. 15, 2013; accepted Sep. 1, 2014
 Water Science and Engineering2014年4期
Water Science and Engineering2014年4期
- Water Science and Engineering的其它文章
- Water Science and Engineering ISSN 1674-2370, CN 32-1785/TV Vol. 3, Nos.1-4 2010 TOTAL CONTENTS
- Sea level change under IPCC-A2 scenario in Bohai, Yellow, and East China Seas
- Simulation-optimization model of reservoir operation based on target storage curves
- Comparison between dynamic programming and genetic algorithm for hydro unit economic load dispatch
- Optimal early refill rules for Danjiangkou Reservoir
- Purification and utilization of garlic processing wastewater in lotus pond wetlands
