Sea level change under IPCC-A2 scenario in Bohai, Yellow, and East China Seas

Chang-lin CHEN, Jun-cheng ZUO*, Mei-xiang CHEN, Zhi-gang GAO, C.-K. SHUM

1. State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, State Oceanic Administration, Hangzhou 310012, P. R. China

2. College of Harbor, Coastal and Offshore Engineering, Hohai University, Nanjing 210098, P. R. China

3. National Marine Date and Information Service, State Oceanic Administration, Tianjin 300171, P. R. China

4. School of Earth Sciences, Ohio State University, Columbus OH 43210, USA

Sea level change under IPCC-A2 scenario in Bohai, Yellow, and East China Seas

Chang-lin CHEN1, Jun-cheng ZUO*2, Mei-xiang CHEN2, Zhi-gang GAO3, C.-K. SHUM4

1. State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, State Oceanic Administration, Hangzhou 310012, P. R. China

2. College of Harbor, Coastal and Offshore Engineering, Hohai University, Nanjing 210098, P. R. China

3. National Marine Date and Information Service, State Oceanic Administration, Tianjin 300171, P. R. China

4. School of Earth Sciences, Ohio State University, Columbus OH 43210, USA

Because of the environmental and socioeconomic impacts of anthropogenic sea level rise (SLR), it is very important to understand the processes leading to past and present SLRs towards more reliable future SLR projections. A regional ocean general circulation model (ROGCM), with a grid refinement in the Bohai, Yellow, and East China Seas (BYECSs), was set up to project SLR induced by the ocean dynamic change in the 21st century. The model does not consider the contributions from ice sheets and glacier melting. Data of all forcing terms required in the model came from the simulation of the Community Climate System Model version 3.0 (CCSM3) under the International Panel on Climate Change (IPCC)-A2 scenario. Simulation results show that at the end of the 21st century, the sea level in the BYECSs will rise about 0.12 to 0.20 m. The SLR in the BYECSs during the 21st century is mainly caused by the ocean mass redistribution due to the ocean dynamic change of the Pacific Ocean, which means that water in the Pacific Ocean tends to move to the continental shelves of the BYECSs, although the local steric sea level change is another factor.

sea level rise; steric sea level change; IPCC-A2 scenario; mass redistribution; Bohai, Yellow, and East China Seas

1 Introduction

Sea level rise (SLR) is one of the most profound consequences of anthropogenic climate change. As coastal ecosystems and their communities around the world are widely recognized to be vulnerable to SLR (Nicholls et al. 2007), it is very important to understand processes governing past and present SLRs and to obtain reliable future SLR projections (Yin et al. 2010).

The global mean SLR from tide gauge records is assessed to have been about 1.7 mm/year in the 20th century and 1.8 mm/year in the period from 1950 to 2000 (Churchet al. 2004; Church and White 2006; Holgate 2007; Bindoff et al. 2007). Altimetry data show a more rapid rate of SLR at 3 mm/year after 1993 (Cazenave and Nerem 2004; Willis et al. 2008). However, the greater value of the estimated SLR rate could be a result of contamination by interannual or longer variations in the ocean. During the past decade, realistic global atmosphere-ocean general circulation models (AOGCMs) were widely used to simulate and project SLR (Gregory et al. 2001; Pardaens et al. 2011a, b; Church et al. 2011). The Fourth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC) projected a global average SLR of between 0.18 m and 0.59 m from 1990 to 2100 using the full range of IPCC greenhouse gas (GHG) scenarios and a range of AOGCMs, including the ice sheet uncertainties (Bindoff et al. 2007). In responding to a changing climate, however, SLR of the global ocean will not be spatially uniform, but will rather display considerable regional patterns, as indicated by both observations and model projections (Douglas 2001; Landerer et al. 2007a; Yin et al. 2010; Suzuki and Ishii 2011; Merrifield 2011).

The Bohai, Yellow, and East China Seas (BYECSs) are shallow marginal seas enclosed by East China, the Korean Peninsula, and Japan, with open connections to the northwest Pacific Ocean, South China Sea, and Sea of Japan (Fig. 1). The BYECSs have one of the most extensive continental shelves in the world. The Okinawa Trough, which is the deepest section in the BYECSs, extends alongside the Ryukyu Island chain and has a maximum depth of 2717 m. Water depth off the coast of the BYECSs is less than 20m, which makes these coastal areas very vulnerable to SLR. In the BYECSs, sea level variability is very complicated (Han and Huang 2008; Zuo et al. 2012), and SLR is apparent over the last 50 years based on the observational data (Yan et al. 2007; Chen et al. 2010).

Previous studies on the projection of SLR with climate change in the BYECSs have been mainly based on simple estimation models. For example, Zhang (1997) set up a simple estimation model, which considers GHG emission to project the SLR along the coast of China. Li et al. (2011) predicted the SLR in the BYECSs using a semi-empirical method based on the relationship between the global surface air temperature and sea level. Simple estimation models are computationally cheap and canprovide insights into how the global SLR is modified through various mechanisms under different GHG emission scenarios. However, these simple models are based on the assumption that SLR in the future will respond to climate change as a linear system, so that the future response is analogous to the past. Furthermore, they are limited by lack of spatial variability (Jevrejeva et al. 2012). In contrast, the AOGCMs can simulate the spatial variations of SLR (Gregory et al. 2001). However, due to the high computational cost, most of the AOGCMs run with relatively coarse horizontal resolutions (about 1°×1° or lower for ocean components). Some continental shelves, e.g., those of the BYECSs, are not well represented by these models. Since the topography and ocean dynamics on these shelves cannot be well reproduced, the patterns and attributes of SLR in these regions are unclear.

In this study, we set up a regional ocean general circulation model (ROGCM) of a portion of the Pacific Ocean with a grid refinement in the BYECSs, to project the SLR in the BYECSs in the 21st century. We only focused on the ocean dynamics that impact the absolute SLR pattern, while excluding the melting of glaciers and ice sheets, the gravitational loading effect that modifies the geoid (Mitrovica et al. 2009), and geological processes such as glacial isostatic adjustment (Peltier 2001) and sea-floor tectonics.

2 Model configuration and analysis methods

2.1 Model description

The simulation described here was performed using the Los Alamos Parallel Ocean Program (POP) (Smith et al. 1992; Smith and Gent 2004), a level-coordinate ROGCM that solves three-dimensional primitive equations with realistic bottom topography. POP is the ocean component of the Community Climate System Model (CCSM) developed by the National Center for Atmospheric Research (NCAR). It is a Bryan-Cox-type model with an implicit free-surface treatment of the barotropic equations (Bryan 1969). The vertically integrated continuity equation in the Boussinesq approximation reads as follows:

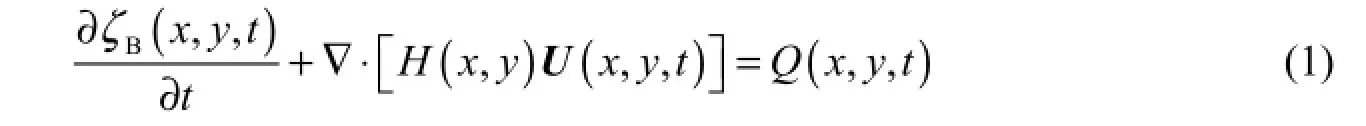
where ζBis the sea surface height (SSH) due to the Boussinesq dynamics, H is the depth of the ocean, Uis the vertically averaged horizontal velocity, and Q represents the surface freshwater flux, which is treated as virtual salt flux here. With the virtual salt flux, the dilution and salinification effects of rainfall and evaporation have to be parameterized by a salt extraction or input, and it is considered that the global hydrological cycle affects the oceanic circulation in the form of a spurious salt cycle (Yin et al. 2010).

Eq. (1) implies volume conservation in the ocean; this formulation yields correct relative horizontal SSH gradients, but a spatially uniform time-varying correction term must be added in order to adjust the sea level for any net expansion or contraction through changes in the mean density in the model domain (Greatbatch 1994). Based on Mellor and Ezer (1995), thenon-Boussinesq SSH (ζ) can be written as

where ζEis the SLR due to expansion or contraction of the water column and is equal to the area average ofbeing the vertical average of density deviation from a reference density, and ρ0being the reference density; and ζGSis unknown and negligible as a small error, which is largely attributable to the so-called Goldsbrough-Stommel gyres (Greatbatch 1994), a non-Boussinesq vortex stretching effect caused by density change.

2.2 Model setup

The model domain extends from 20°S to 65°N and from 98°E to 60°W. The horizontal grid is a non-uniform Mercator grid (Fig. 2). In order to sufficiently represent the BYECSs, the horizontal resolution of the domain (113°E to 132°E, and 22°N to 42°N) is 0.25° and gradually changes to 1° and 2° outside.

Fig. 2 Model grid (black lines are plotted every two points) and topography

In this study there were 40 non-uniform vertical levels, which varied in thickness from about 10 m at the surface to 250 m at depth. The topography was derived from the 1/12° ETOP05 database of the National Geophysical Data Center (NGDC). The depth of the BYECSs was replaced with the bathymetry data provided by the Navigation Assurance Ministry of the Chinese Navy Headquarters, and interpolated to model grids to provide more accurate ocean topography.

Biharmonic operators were used for horizontal mixing of momentum and tracers. The horizontal viscosity and diffusivity varied spatially with the cube of the horizontal grid spacing and had equatorial values of 2.7 × 1010m4/s and 0.9 × 1010m4/s, respectively. The vertical viscosity and diffusivity were computed using the Richardson number formulation(Pacanowski and Philander 1981) with background values of 10-4m2/s and 10-5m2/s, respectively.

The model was driven by surface wind and boundary forcing. The surface heat and freshwater fluxes were calculated from bulk flux formulations. Necessary forcing fields consisted of sea surface wind stress, sea surface temperature, air temperature, air humidity, downward short-wave radiation, cloud fraction, wind speed, sea surface salinity, and precipitation. All these fields were derived from the simulation result of the CCSM version 3.0 (CCSM3) under the IPCC-A2 scenario. Restoring buffer zones with a width of 3° were set near the four lateral boundaries where the temperature and salinity were restored to the monthly values of CCSM3 output data at all depths with a restoring time scale of 30 days. The A2 scenario is a medium-high emission scenario that is widely used in regional climate change research (Cayan et al. 2007; Tang et al. 2009; Graham et al. 2012).

The model was initialized with the ocean at rest, and the temperature and salinity were set to the values of January 2000 in the CCSM3 IPCC-A2 experiment. Then, the model was spun up from January 2000 to December 2009 with a time step of 24 minutes, driven by the forcing described above. This completed a 10-year spinup. After that, we switched the model back to January 2000, and spun it up again for other nine rounds. In total a 100-year spinup was completed. Then, the model was run from January 2000 through December 2099. The monthly mean SSH, temperature, and salinity data were then used for analysis.

2.3 Analysis methods

Sea level change (Δζ) can be attributed to three major components:

where Δhsis the local steric sea level change; Δpbgρ0is the sea level change induced by bottom pressure change, with pbbeing the bottom pressure, and g being the gravitational acceleration; and Δhais the atmospheric inverse barometer correction to the sea level change. In the present study, Δha=0.

The local steric sea level change is associated with vertical expansion or contraction of the water column in response to changes in the local density. It is necessary to convert the gridded temperature and salinity anomalies to density anomalies at each standard level using the classical expression for the ocean state equation (Gill 1982). The local steric sea level change is further obtained by vertically integrating density anomalies at each grid point and each time step according to the following equation (Lombard et al. 2005):

where S, T, and p are the salinity, temperature, and pressure, respectively, and S0and T0are the values in the reference state. ρ is a nonlinear function of S, T, and p (Gill 1982).

3 Results and discussion

3.1 Projection of SLR in BYECSs

First of all, annual mean values of variables were calculated from the monthly mean output of the model. The time series of SLR in the Pacific Ocean (98°E to 60°W, 20°S to 65°N) was obtained from the averaged local steric sea level change. By the end of the 21st century, the projected SLR in the Pacific Ocean is about 0.18m with a significant acceleration (Fig. 3). This implies that the net heat flux into the ocean is increasing steadily (Gregory et al. 2001). The rising value is much smaller than the global mean projected SLR over the 21st century, which is about 0.30m under the IPCC-A2 scenario (see Fig. 3(c) in Meehl and Washington 2006). The same result is shown in Landerer et al. (2007a).

As the POP model used in this study is based on a Boussinesq approximation, a correction term (ζE) must be applied to SSH according to Eq. (2), where ζEis the spatially uniform time-varying area-averaged SLR of the Pacific Ocean (Fig. 3). After adding ζEto the SSH of the model output in the Boussinesq approximation ζB, the non-Boussinesq SSH ζ was obtained, and the sea level change in the BYECSs was further obtained, as shown in Fig. (4).

Fig. 3 Mean SLR over model domain

Fig. 4 Projections of SLR in BYECSs from 2090 to 2099 relative to 2000 to 2009

The projected SLR ranges from 0.12 to 0.20 m in the BYECSs (Fig. 4). The value is largein the sea area near the Ryukyu Island chain connected to the Northwestern Pacific Ocean, where the bathymetry is deeper than 200 m, and relatively low on the continental shelves. The SLR in the Bohai Sea reaches 0.17 m; the rise in amplitude is more than 0.16 m in the eastern part of the Yellow Sea and East China Sea, a little larger than that in the western part of the BYECSs, where it is is less than 0.15 m.

3.2 Local steric SLR

The local steric SLR was calculated with Eq. (4). The local steric SLR is positive for all regions in the BYECSs (Fig. 5(a)). A large value also occurs near the Ryukyu Island chain, which reaches 0.20 m. In contrast, shallow water columns on the continental shelves of the BYECSs only permit a much smaller steric expansion than the deep water region. This steric SLR pattern demonstrates a sharp gradient across the Kuroshio (Landerer et al. 2007b). On the continental shelves, the steric SLR ranges from 0.02 to 0.08 m, with a relatively larger value in the offshore area, and a smaller value near the coastline (Fig. 5(a)). In general, the steric SLR contributes less than 50% to the total projected SLR, and the contribution is even smaller near the coastal region, with a ratio of less than 20% (Fig. 5(b)). The steric SLR can be divided into thermosteric and halosteric SLRs. Almost all of the steric SLR on the continental shelves is induced by the thermosteric effect. However, the steric SLR off the Kuroshio largely results from the halosteric effect (figures omitted).

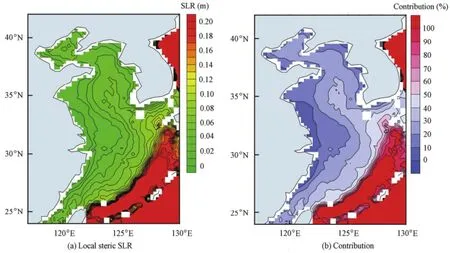
Fig. 5 Local steric SLR from 2090 to 2099 relative to 2000 to 2009 and its contribution to total projected SLR

3.3 SLR induced by mass redistribution

From the difference between the projected SLR (Fig. 4) and local steric SLR (Fig. 5(a)), the contribution of bottom pressure change to the total projected SLR for the period of 2090 to 2099 relative to the period of 2000 to 2009 was obtained. The contribution of the bottompressure change (Δ pbgρ0) is caused by ocean mass redistributions which result from tides, ocean circulation changes, or water mass flux such as the global water cycle or melting of glaciers and ice sheets. In the CCSM3 and POP models, the contributions to SLR from ice sheets and glacier melting are not included, and freshwater flux is treated as virtual salt flux. Hence, all of the bottom pressure changes are considered solely from the ocean mass redistributions induced by the ocean dynamic change. Most prominently, an additional mass loading that can cause a SLR of up to 0.13 m occurs on the continental shelves of the BYECSs, where the water depth is less than 200 m, while the effect is very small in the deep water region (Fig. 6(a)). The pattern effectively reduces the strong local steric SLR gradient across the Kuroshio. This means that sea water tends to move from the Pacific Ocean to the continental shelves of the BYECSs. On the continental shelves of the BYECSs, the mass redistribution-induced SLR is closely related to the water depth, with the value ranging from 0.09 m in the offshore area to 0.15 m in the coastal area (Fig. 6(a)). In general, mass redistribution-induced SLR contributes more than 50% to the total projected SLR on the continental shelves of the BYECSs, and the contribution is even larger near the coastal region, with a ratio of more than 80% (Fig. 6(b)).

Fig. 6 SLR induced by mass redistribution from 2090 to 2099 relative to 2000 to 2009 and its contribution to total projected SLR

4 Conclusions

(1) A ROGCM of the Pacific Ocean, with a grid refinement in the BYECSs, was established to project the SLR in the BYECSs in the 21st century. Simulation results show that, at the end of the 21st century, the sea level in the BYECSs will rise about 0.12 to 0.20 m. SLR in the Bohai Sea is relatively large, reaching 0.17 m. The rise in amplitude in the eastern BYECSs is larger than that in the western BYECSs. The sea level will rise about 0.20 m nearthe Ryukyu Islands.

(2) The contributions of different factors to SLR can be divided into the ocean mass redistribution and local steric sea level change. In summary, the SLR in the BYECSs over the 21st century will mainly be due to the ocean mass redistribution caused by the ocean dynamic change, which means that sea water will tend to move from the Pacific Ocean to the continental shelves of the BYECSs. This also implies that, with global warming, the SLR in the BYECSs, to a great extent, will be determined by Pacific Ocean-scale changes, rather than by local changes.

(3) In the study, it is considered that only the ocean dynamics affect the absolute SLR patterns. The model does not include contributions from ice sheets, glacier melting, and land movements. Tidal contributions are also negligible in the low-frequency change analysis. Thus, the projected SLR in this study is smaller than those in the previous studies, which were based on simple estimation models. For example, Zhang (1997) and Li et al. (2011) showed that the SLR in the BYECSs at the end of the 21st century would be about 0.28 to 0.64 m and 0.30 to 0.74 m, respectively.

(4) Results in this study were obtained from one ROGCM, which contains uncertainties in modeling of climate change. Therefore, the results only suggest a possible estimation of SLR in the BYECSs under the IPCC-A2 scenario. In future studies, SLR should be projected with different models under different emission scenarios so as to provide a more representative prediction range.

Bindoff, N. L., Willebrand, J., Artale, V., Cazenave, A., Gregory, J., Gulev, S., Hanawa, K., Le Quéré, C., Levitus, S., Nojiri, Y., et al. 2007. Observations: Oceanic climate change and sea level. Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K. B., Tignor, M., and Miller, H. L., eds., Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, 386-432. Cambridge: Cambridge University Press.

Bryan, K. 1969. A numerical method for the study of the circulation of the world ocean. Journal of Computational Physics, 4(3), 347-376.

Cayan, D. R., Maurer, E. P., Dettinger, M. D., Tyree, M., and Hayhoe, K. 2008. Climate change scenarios for the California region. Climatic Change, 87(s1), 21-42. [doi:10.1007/s10584-007-9377-6]

Cazenave, A., and Nerem, R. S. 2004. Present-day sea level change: Observations and causes. Reviews of Geophysics, 42(3), RG3001. [doi:10.1029/2003RG000139]

Chen, M. C., Zuo, J. C., Chen, M. X., Zhang, J. L., and Du, L. 2007, Spatial distribution of sea level trend and annual range in the China Seas from 50 long term tidal gauge station data. Proceedings of the Eighteenth International Offshore and Polar Engineering Conference, 583-587. Vancouver: ISOPE.

Church, J. A., White, N. J., Coleman, R., Lambeck, K., and Mitrovica, J. X. 2004. Estimates of the regional distribution of sea level rise over the 1950 to 2000 period. Journal of Climate, 17(13), 2609-2625. [doi:10.1175/1520-0442(2004)017〈2609:EOTRDO〉2.0.CO;2]

Church, J. A., and White, N. J. 2006. A 20th century acceleration in global sea-level rise. Geophysical Research Letters, 33(1), 01602. [doi:10.1029/ 2005GL024826]

Church, J. A., Gregory, J. M., White, N. J., Platten, S. M., and Mitrovica, J. X. 2011. Understanding and projecting sea level change. Oceanography, 24(2), 130-143. [doi:10.5670/oceanog.2011.33]

Douglas, B. C. 2001. Sea level change in the era of the recording tide gauge. Douglas, B. C., Kearney, M. S., andLeatherman, S. P., eds., Sea Level Rise: History and Consequence, 37-62. New York: Academic Press.

Gill, A. E. 1982. Atmosphere-Ocean Dynamics, 662. San Diego: Academic Press.

Graham, N. E., Cayan, D. R., Bromirski, P. D., and Flick, R. E. 2012. Multi-model projections of twenty-first century North Pacific winter wave climate under the IPCC A2 scenario. Climate Dynamics, 40(5-6), 1335-1360. [doi:10.1007/s00382-012-1435-8]

Greatbatch, R. J. 1994. A note on the representation of steric sea level in model that conserve volume rather than mass. Journal of Geophysical Research, 99(C6), 12767-12771. [doi:10.1029/94JC00847]

Gregory, J. M., Church, J. A., Boer, G. J., Dixon, K. W., Flato, G. M., Jackett, D. R., Lowe, J. A., O'Farrell, S. P., Roeckner, E., Russell, G. L., et al. 2001. Comparison of results from several AOGCMs for global and regional sea-level change 1900-2100. Climate Dynamics,18(3-4), 225-240. [doi:10.1007/s003820100180]

Han, G. Q., and Huang, W. G. 2008. Pacific decadal oscillation and sea level variability in the Bohai, Yellow, and East China Seas. Journal of Physical Oceanography, 38(12), 2772-2783. [doi:10.1175/2008JPO3885.1]

Holgate, S. J. 2007. On the decadal rates of sea level change during the twentieth century. Geophysical Research Letters, 34(1), L01602. [doi:10.1029/2006GL028492]

Jevrejeva, S., Moore, J. C., and Grinsted, A. 2012. Sea level projections to AD2500 with a new generation of climate change scenarios. Global and Planetary Change, 80-81, 14-20. [doi:10.1016/j.gloplacha. 2011.09.006]

Landerer, F. W., Jungclaus, J. H., and Marotzke, J. 2007a. Regional dynamic and steric sea level change in response to the IPCC A1B scenario. Journal of Physical Oceanography, 37(2), 296-312. [doi: 10.1175/JPO3013.1]

Landerer, F. W., Jungclaus, J. H., and Marotzke, J. 2007b. Ocean bottom pressure changes lead to a decreasing length-of-day in a warming climate. Geophysical Research Letters, 34(6), L06307. [doi:10.1029/ 2006GL029106]

Li, X., Zhang, J., and Gao, Z. 2011. Discussion on semi-empirical prediction method for sea level change of China. Marine Sciences Bulletin, 30(5), 540-543. (in Chinese)

Lombard, A., Cazenave, A., Le Traon, P. Y., and Ishii, M. 2005. Contribution of thermal expansion to present-day sea level change revisited. Global and Planetary Change, 47(1), 1-16. [doi: 10.1016/j.gloplacha.2004.11.016]

Meehl, G. A., and Washington, W. M. 2006. Climate change projections for the twenty-first century and climate change commitment in the CCSM3. Journal of Climate, 19(11), 2597-2616. [doi:10.1175/JCLI3746.1]

Mellor, G. L., and Ezer, T. 1995. Sea level variations induced by heating and cooling: An evaluation of the Boussinesq approximation in ocean models. Journal of Geophysical Research, 100(C10), 20565-20577. [doi:10.1029/95JC02442]

Merrifield, M. A. 2011. A shift in western tropical Pacific sea level trends during the 1990s. Journal of Climate, 24(15), 4126-4138. [doi:10.1175/2011JCLI3932.1]

Mitrovica, J. X., Gomez, N., and Clark, P. U. 2009. The sea-level fingerprint of west Antarctic collapse. Science, 323(5915), 753. [doi:10.1126/science.1166510]

Nicholls, R. J., Wong, P. P., Burkett, V. R., Codignotto, J. O., Hay, J. E., McLean, R. F., Ragoonaden, S., and Woodroffe, C. D. 2007. Coastal systems and low-lying areas. Parry, M. L., Canziani, O. F., Palutikof, J. P., van der Linden, P. J., and Hanson, C. E., eds., Climate Change 2007: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, 315-357. Cambridge: Cambridge University Press.

Pacanowski, R. C., and Philander, S. G. H. 1981. Parameterization of vertical mixing in numerical models of tropical oceans. Journal of Physical Oceanography, 11(11), 1443-1451. [doi:10.1175/1520-0485(1981) 011〈1443:POVMIN〉2.0.CO;2]

Pardaens, A. K., Gregory, J. M., and Lowe, J. A. 2011a. A model study of factors influencing projected changes in regional sea level over the twenty-first century. Climate Dynamics, 36(9), 2015-2033. [doi:10.1007/ s00382-009-0738-x]

Pardaens, A. K., Lowe, J. A., Brown, S., Nicholls, R. J., and de Gusmão, D. 2011b. Sea level rise and impacts projections under a future scenario with large greenhouse gas emission reductions. Geophysical ResearchLetters, 38(12), L12604. [doi:10.1029/2011GL047678]

Peltier, W. R. 2001. Global glacial isostatic adjustment and modern instrumental records of relative sea level history. Douglas, B. C., Kearney, M. S., and Leatherman, S. P., eds., Sea Level Rise: History and Consequences, 65-95. New York: Academic Press.

Smith, R., and Gent, P. 2004. Reference Manual for the Parallel Ocean Program (POP). Los Alamos: Los Alamos National Laboratory.

Smith, R. D., Dukowicz, J. K., and Malone, R. C. 1992. Parallel ocean general circulation modeling. Physica D: Nonlinear Phenomena, 60(1-4), 38-61. [doi:10.1016/0167-2789(92)90225-C]

Suzuki, T., and Ishii, M. 2011. Regional distribution of sea level changes resulting from enhanced greenhouse warming in the model for interdisciplinary research on climate version 3.2. Geophysical Research Letters, 38(2), L02601. [doi:10.1029/2010GL045693]

Tang, J. P., Chen, X., Zhao, M., and Su, B. K. 2009. Numerical simulation of regional climate change under IPCC A2 scenario in China. ActaMeteorologica Sinica, 23(1), 29-42.

Willis, J. K., Chambers, D. P., and Nerem, R. S. 2008. Assessing the globally averaged sea level budget on seasonal to interannual timescales. Journal of Geophysical Research, 113(C6), C06015. [doi:10.1029/ 2007JC004517]

Yan, M., Zuo, J. C., Du, L., Li, L., and Li, P. L. 2007. Sea level variation/change and steric contributions in the East China Sea. Proceedings of the Seventeenth International Offshore and Polar Engineering Conference, 2377-2382. Lisbon: ISOPE.

Yin, J. J., Griffies, S. M., and Stouffer, R. J. 2010. Spatial variability of sea level rise in twenty-first century projections. Journal of Climate, 23(17), 4585-4607. [doi:10.1175/2010jcli3533.1]

Zhang, J. W. 1997. Estimate model of MSL change along the coast of China. Marine Science Bulletin, 16(4), 1-9. (in Chinese)

Zuo, J. C., He, Q. Q., Chen, C. L., Chen, M. X., and Xu, Q. 2012. Sea level variability in the East China Sea and its respond to ENSO. Water Science and Engineering, 5(2), 164-174. [doi:10.3882/j.issn.1674-2370.2012.02.005]

(Edited by Ye SHI)

This work was supported by the National Natural Science Foundation of China (Grants No. 41206021 and 41276018), the National Basic Research Program of China (Grant No. 2012CB955601), the Young Scientist Foundation of the State Oceanic Administration, China (Grant No. 2012251), the U.S. National Science Foundation Belmont Forum Program (Grant No. ICER-1342644), and the GASI-03-01-01-09.

*Corresponding author (e-mail: zuo@ouc.edu.cn)

Received Aug. 24, 2013; accepted Jun. 30, 2014