A simplified dynamic method for field capacity estimation and its parameter analysis
Zhen-tao CONG*, Hua-fang LÜ, Guang-heng NI
Department of Hydraulic Engineering, Tsinghua University, Beijing 100084, P. R. China
A simplified dynamic method for field capacity estimation and its parameter analysis
Zhen-tao CONG*, Hua-fang LÜ, Guang-heng NI
Department of Hydraulic Engineering, Tsinghua University, Beijing 100084, P. R. China
This paper presents a simplified dynamic method based on the definition of field capacity. Two soil hydraulic characteristics models, the Brooks-Corey (BC) model and the van Genuchten (vG) model, and four soil data groups were used in this study. The relative drainage rate, which is a unique parameter and independent of the soil type in the simplified dynamic method, was analyzed using the pressure-based method with a matric potential of −1/3 bar and the flux-based method with a drainage flux of 0.005 cm/d. As a result, the relative drainage rate of the simplified dynamic method was determined to be 3% per day. This was verified by the similar field capacity results estimated with the three methods for most soils suitable for cultivating plants. In addition, the drainage time calculated with the simplified dynamic method was two to three days, which agrees with the classical definition of field capacity. We recommend the simplified dynamic method with a relative drainage rate of 3% per day due to its simple application and clearly physically-based concept.
field capacity; simplified dynamic method; pressure-based method; flux-based method; soil water; HYDRUS
1 Introduction
Field capacity is widely used as an important concept and parameter in irrigation management, hydrological modeling, and ecohydrological studies. In irrigation management, the field capacity represents available soil water content, and irrigation depth is adjusted so that the soil water content can reach its field capacity (Brouwer et al. 1989). In hydrological modeling, the field capacity is an important parameter for simulating infiltration and evapotranspiration (Singh 1995). For example, in the SWAT catchment model, percolation occurs when the water content of soil layers exceeds the field capacity (Neitsch et al. 2005). In ecohydrological studies on water-controlled ecosystems, the field capacity is often used as a reference value triggering the control of soil water over plant water uptake (Rodríguez-Iturbe and Porporato 2004).
The field capacity has been defined in various ways. According to the classical definition given by Veihmeyer and Hendrickson (1931), the field capacity is the amount of water held insoil after excess water has drained away, and the rate of water downward movement has materially decreased, which usually takes place within two to three days after a rain event or irrigation in pervious soils of uniform structure and texture. Although this definition is conceptually intuitive and sound, it does not provide a quantitative measure with respect to the time when excess water has drained away and when the rate of water downward movement has materially decreased after free drainage is negligible (Hillel 1998).
Quantitative measurement is indispensable for estimating the field capacity in experiments, and typically involves wetting a covered soil profile and waiting for drainage to cease (Twarakavi et al. 2009). Such measurement can measure a matric potential or a drainage flux that represents the field capacity status. The pressure-based method was introduced by Richards and Weaver (1944) to estimate the field capacity with the soil water content at a matric potential of −1/3 bar (equivalent to −33 kPa and −348 cm of water column) based on their laboratory experiments. The choice of −1/3 bar was confirmed in a later study by Colman (1947), and it has been widely adopted in modern hydrology (Dingman 1994; Hillel 1998). The field capacity defined through the matric potential varies with the soil texture, depending on the soil water retention characteristics. Romano and Santini (2002) suggested the use of a matric potential of −100 cm of water column for sandy soils, −350 cm of water column for medium-textured soils, and −500 cm of water column for clayey soils, to reflect their different water retention characteristics. On the other hand, the flux-based method proposed by Nachabe (1998) estimates the field capacity with the soil water content at a free drainage flux of 0.005
cm/d, which is two orders of magnitude lower than the average potential evapotranspiration. In Nachabe (1998), it was assumed that the water content was uniform within a given soil horizon after a period of infiltration and remained that way during drainage, meaning that water flow occurred solely in response to the gravity, and the free drainage flux was equal to the unsaturated soil hydraulic conductivity. This assumption is reasonable according to the definition of field capacity with free drainage at the bottom, and it is easily verified with the HYDRUS-1D model. This approach is equivalent to determining the soil water content at a given unsaturated hydraulic conductivity based on the unsaturated hydraulic conductivity model. The field capacity defined based on the drainage flux also varies with the soil texture. For example, Meyer and Gee (1999) suggested estimating the field capacity with the soil water content at a free drainage flux of 0.001 cm/d for sand and 0.01 cm/d for clay, and Sun and Yang (2013) took the value of 0.01 cm/d of the drainage flux.
These two static methods, i.e., the pressure-based method and the flux-based method, are straightforward and simple. However, they are inadequate for characterizing the dynamic process of water drainage from soils after wetting events and accounting for the influence of other important factors, such as the soil thickness, on the estimated field capacity. The dynamic method, on the other hand, estimates the field capacity by simulating the soil water dynamics after wetting events. The boundary conditions used in the dynamic method are free drainage at the bottom and zero flux at the top, which are consistent with the field capacity definitions. In Zacharias and Bohne (2008), the soil water dynamics after a wetting event in a100cm-thick soil column were simulated using the HYDRUS-1D model, and the field capacity was taken as the soil water content after 15 days of drainage or when the daily change of soil water storage fell below 1%. Twarakavi et al. (2009) used the HYDRUS-1D model to simulate changes in the soil water content till the drainage flux reached predefined reference values, i.e., 0.001, 0.01, and 0.1 cm/d in their study, in which the soil water content at the bottom of the soil column was taken as the field capacity. Twarakavi et al. (2009) also compared the field capacities estimated at different soil thicknesses (1 cm, 10 cm, and 100 cm), which were found to produce similar estimates of the field capacity but different estimates of the drainage time. Since the water content is uniform for different depths, the approach of Twarakavi et al. (2009) is essentially the same as the flux-based method.
For both the pressure-based and flux-based methods, the main challenge is that the reference values used to determine the field capacity are dependent on the soil texture and soil water retention characteristics. For the dynamic method, the main challenge is to solve the Richards equation using some numerical models such as the HYDRUS-1D model. The objectives of this study were (1) to present a simplified dynamic method without numerical simulation, (2) to select a special relative drainage rate that does not vary with the soil texture, and (3) to compare field capacities estimated with the proposed method and static methods using the soil data groups in Clapp and Hornberger (1978), Rawls et al. (1982), Carsel and Parrish (1988), and Twarakavi et al. (2009).
2 Materials and methods
2.1 Soil hydraulic characteristics
The soil water retention curve and soil hydraulic conductivity play critical roles in static and dynamic methods for estimating the field capacity. Soil hydraulic characteristics are usually measured experimentally, and their nonlinear functions are then fitted with the experimental data. Several empirical models have been proposed to describe the two hydraulic functions, of which the Brooks and Corey (BC) model (Brooks and Corey 1964; Campbell 1974) and the van Genuchten (vG) model (van Genuchten 1980) are the most widely adopted. The BC model is defined as

where ψ (Θ) is the matric potential in cm; ψaeis the air entry potential in cm; Θ is the effective saturation, and Θ = (θ − θr)(θs− θr), with θ being the volumetric water content in cm3/cm3, and θsand θrbeing the saturated and residual water contents in cm3/cm3, respectively; K (Θ) is the soil hydraulic conductivity in cm/d; Ksis the saturated soil hydraulic conductivity in cm/d; b is the pore-size distribution index; and c is the pore disconnectedness index. The parameters b and c are normally connected through c= 2 b+ 3.
The vG model is defined as

where α is in cm−1, and n and m are the shape parameters with m=1−1n . The hydraulic conductivity model in Eq. (4) is based on Mualem’s model (Mualem 1976) for predicting the hydraulic conductivity using soil water retention data.
2.2 Pressure-based method and flux-based method
For the pressure-based method, the field capacity is determined from the soil water retention curve (Dingman 1994; Hillel 1998). With the matric potential under the field capacity conditions, the corresponding field capacity is derived from Eq. (1) with the BC model or from Eq. (3) with the vG model. The equations based on the BC model and the vG model are respectively,

where θfcis the field capacity in cm3/cm3, and ψfcis the corresponding matric potential in cm.
For the flux-based method, the field capacity can be estimated from the unsaturated soil hydraulic conductivity function with a predefined negligible free drainage flux. With the unsaturated soil hydraulic conductivity under the field capacity conditions, the field capacity is derived from Eq. (2) with the BC model or from Eq. (4) with the vG model. If the BC model is used, the field capacity can be estimated as
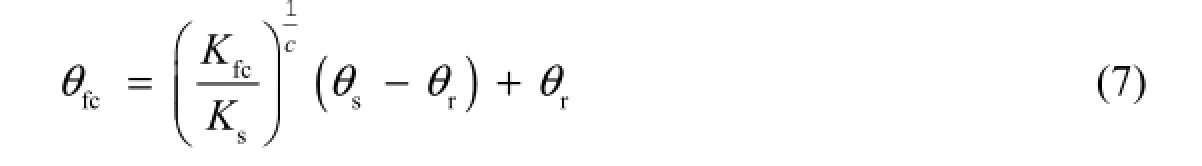
where Kfcis the unsaturated soil hydraulic conductivity, as well as the drainage flux under the field capacity conditions, in cm/d. For the vG model, the analytical solution is unavailable, and the solution needs to be soughtnumerically.
2.3 Simplified dynamic method
We propose a simplified dynamic method for estimating the field capacity based on the change in soil water storage without solving the Richards equation. Under the field capacity conditions, water is held in a soil column with a thickness of D, and the water storage is θfcD. With an assumption of a homogeneous soil profile, the change of soil water storage over a unit time is Kfc. If we define the relative drainage rate as a small percentage (such as 1% per day) ofthe water storage under the field capacity conditions, the field capacity can be estimated using

where δ is the relative drainage rate in d-1.
Using the BC model defined in Eq. (2), Eq. (8) becomes

Using the vG model with the unsaturated soil hydraulic conductivity, Eq. (8) yields
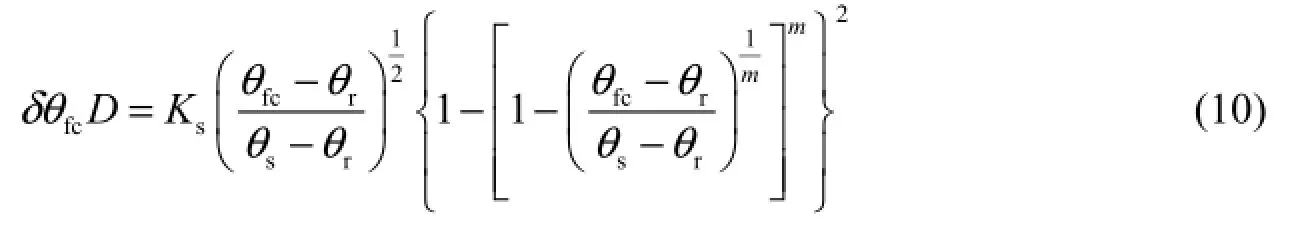
Based on Eq. (9) and Eq. (10), the field capacity can be calculated with the trial and error method when Ks, θs, θr, and the parameters in the BC or vG models are known.It is apparent in Eqs. (9) and (10) that, for a given soil texture and relative drainage rate δ, the estimation of field capacity isaffected by the soil column thickness. In the experiment of Veihmeyer and Hendrickson (1931), the soil column thickness was 1 cm, because it was more reasonable to assume the uniform soil water content when the soil column thickness was small. Thus, we selected a soil column thickness of 1 cm for estimation of the field capacity with the simplified dynamic method in this study.
Another result that we want is the drainage time. Based on the BC model and the assumption that the soil water is in a rectangular distribution, we can obtain

where q is the drainage flux at the average effective saturation Θ.
According to the water balance equation, we have

This method is similar to but a bit different from that of Nachabe (1998) in that the soil thickness is constant in this method, while it is variable in Nachabe (1998). Substituting Eq. (11) into Eq. (12) and after integration, we can obtain the effective saturation of the soil profile:
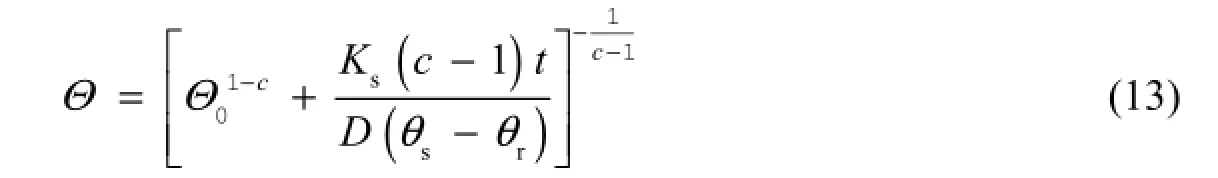
where Θ0is the initial effective saturation. According to the definition of field capacity, the drainage process begins at a saturation point. Thus, Θ0=1. Then, the time to reach the field capacity can be determined from

For the simplified dynamic method, the field capacity and the drainage time for a certain soil type can be estimated with the independent parameter δ. This parameter δ does not depend on the soil type, and it was determined to be 3% per day in this study based on the following discussion.
2.4 Soil data
The parameters of both the BC and vG models vary with soil properties, such as the soil texture, bulk density, and others. Site-specific measurements to determine the parameters of the BC or vG model are often time-consuming and expensive. It is therefore a common practice to search for the parameters of a similar soil from published sources, or to estimate the model parameters from basic soil data (such as the texture, bulk density, etc.) through pedotransfer functions that are developed based on large databases (Schaap et al. 2001). The large databases available in the international community, such as the unsaturated soil hydraulic property database (UNSODA; Leij 1996), the database of hydraulic properties of European soils (HYPRES; Wösten et al. 1999), and the database of the world inventory of soil emission potentials (WISE; Batjes 1996), provide great opportunities for developing alternative pedotransfer functions. In this study, the model parameters corresponding to various soil textures were compiled from some sources that are used widely. For the BC model, the soil data groups were collected from the following sources: (1) 1 845 samples from Dingman (1994) based on Clapp and Hornberger (1978), and (2) 2 541 soil samples from soil data in HYDRUS-1D software based on Rawls et al. (1982). For the vG model, the soil data groups were collected from the following sources: (1) 4 510 soil samples from soil data in HYDRUS-1D software based on Carsel and Parrish (1988), and (2) 1 578 soil samples from Twarakavi et al. (2009). The parameters of those soils are listed in Table 1 and Table 2.
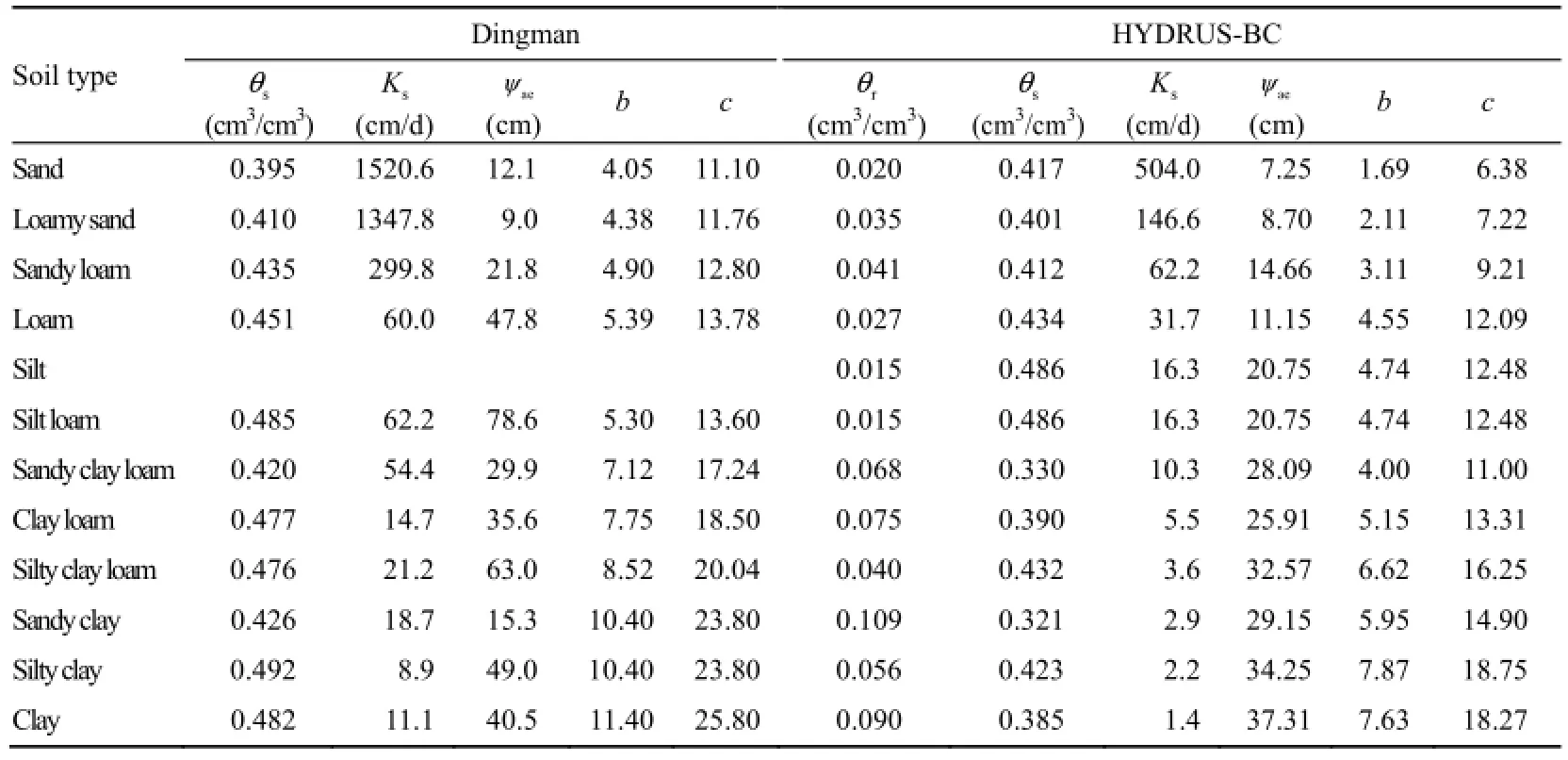
Table 1 Soil data groups of BC model
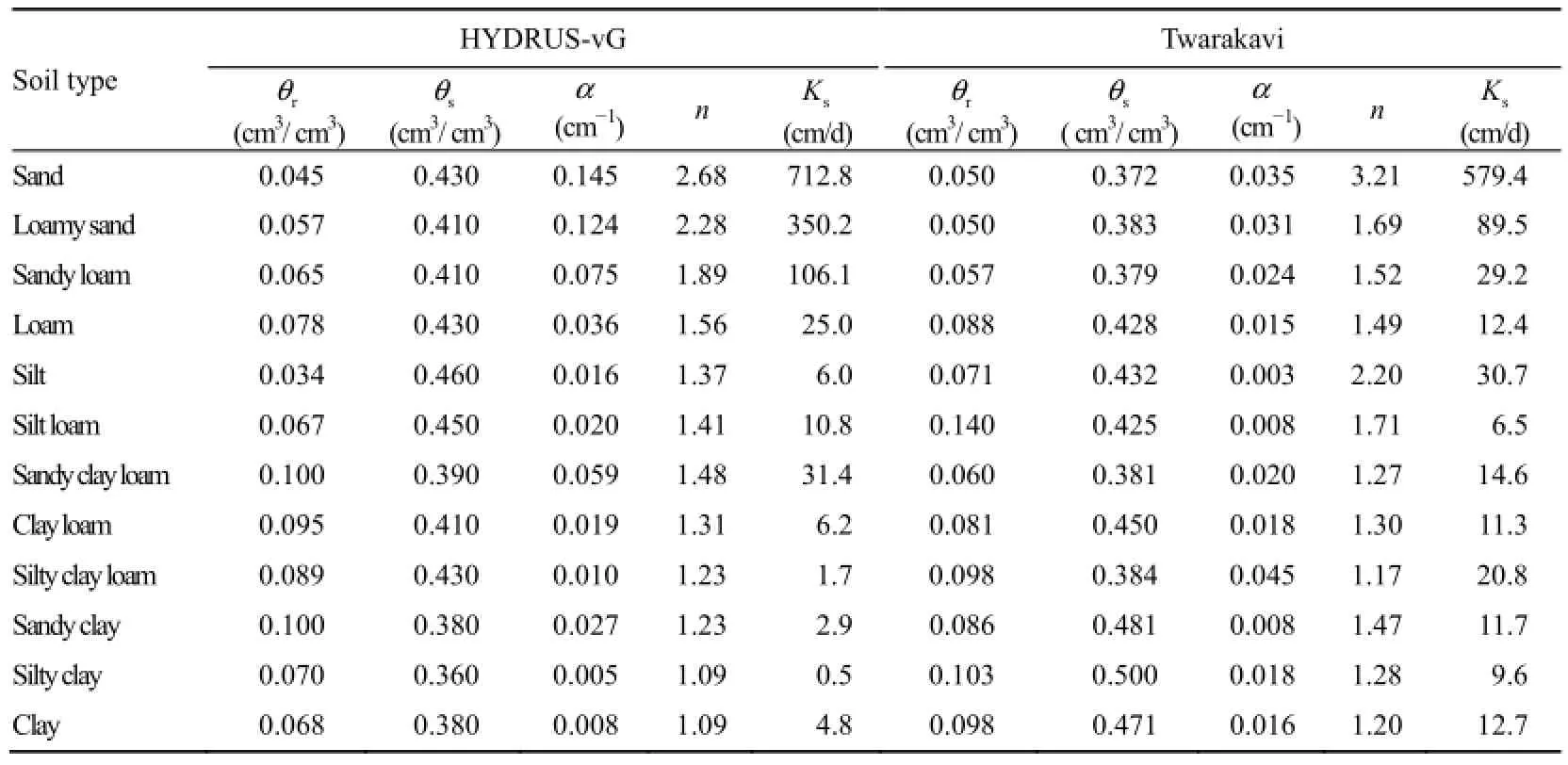
Table 2 Soil data groups of vG model
3 Relative drainage rate analysis
3.1 Relative drainage rate analysis using pressure-based method
Taking δ to be 1%, 2%, 3%, 4%, and 5% per day, respectively, we could calculate the field capacity using Eqs. (9) and (10). Then, the matric potential corresponding to the calculated field capacity could be estimated with Eqs. (1) and (3). The results of four soil data groups can be found in Fig. 1, which indicates that a higher relative drainage rate corresponds to a lower absolute value of the matric potential. For the BC model with its parameters obtained from HYDRUS-BC (Fig. 1(a)), when δ is taken to be 3% per day, the matric potential is close to −1/3 bar (equivalent to −348 cm of water column), which is a value usually used in the pressure-based method for most soils suitable for cultivating plants, such as sandy loam, silt loam, and clay loam. For the BC model with its parameters obtained from Dingman (1994), the results of matric potential corresponding to the calculated field capacity have larger values because the parameters of this group are quite different from those of HYDRUS-BC (Fig. 1(a)). Thus, the Dingman (1994) results cannot be used to determine the relative drainage rate with the pressure-based method. For the vG model (Fig. 1(b)), the lower δ may also lead to a similar matric potential value to that of the BC model with its parameters obtained from HYDEUS-BC. The soil data groups from Twarakavi et al. (2009) and HYDRUS-vG also have similar results, except that for silt in Twarakavi et al. (2009), the matric potential corresponding to the field capacity obtained with the simplified dynamic method is very high because the parameter α of this soil is obviously smaller than that of other soils. Based on this analysis, it is reasonable to use a relative drainage rate δ of 3% per day in the simplified dynamic method for field capacity estimation.
Furthermore, we can also see in Fig. 1 that the matric potential corresponding to the field capacity obtained with the simplified dynamic method varies with the soil texture for a certainvalue of δ. Usually, coarse soil has a smaller absolute value of matric potential, while fine soil has a larger absolute value of matric potential for the same value of the relative drainage rate. This is consistent with the result of Romano and Santini (2002), who used a matric potential of −100 cm of water column for sandy soil, −350 cm of water column for medium-textured soil, and −500 cm of water column for clayey soil.
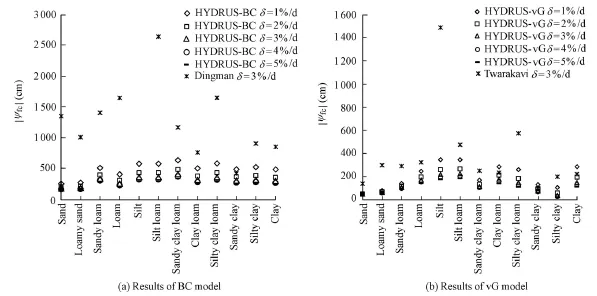
Fig. 1 Matric potential corresponding to field capacity obtained with simplified dynamic method and different values of relative drainage rate
3.2 Relative drainage rate analysis using flux-based method
The drainage flux corresponding to the field capacity calculated with the simplified dynamic method and different values of δ can be estimated with Eqs. (2) and (4). The results of the four soil data groups can be found in Fig. 2, which shows that a higher relative drainage rate corresponds to a higher drainage flux. For the BC model (Fig. 2(a)), when δ is taken to be 3% per day, the drainage flux is about 0.005 to 0.010 cm/d, which is a value usually used in the flux-based method for most soils suitable for cultivating plants, such as sandy loam, silt loam, and clay loam. For the vG model, similar results are shown in Fig. 2(b). We also find that the soil data groups from HYDRUS-BC and Dingman (1994) have similar results for the BC model (Fig. 2(a)), and that the soil data group from Twarakavi et al. (2009) also has a similar result to that from HYDRUS-vG for the vG model (Fig. 2(b)). Based on this analysis, it is reasonable to use a relative drainage rate δ of 3% per day in the simplified dynamic method for field capacity estimation.
Fig. 2 also shows that the drainage flux corresponding to the field capacity obtained with the simplified dynamic method varies with the soil texture for a certain value of δ. Usually, coarse soil has a smaller drainage flux, while fine soil has a larger drainage flux for the same value of the relative drainage rate. This is consistent with the result of Meyer and Gee (1999) who used a free drainage flux of 0.001 cm/d for sand and 0.01 cm/d for clay.

Fig. 2 Drainage flux corresponding to field capacity obtained with simplified dynamic method and different values of relative drainage rate
3.3 Relative drainage rate and drainage time
Based on the field capacity estimated with the simplified dynamic model, the drainage times of different soil data groups with different relative drainage rates were calculate with Eq. (14) (Fig. 3). The results show that a higher relative drainage rate corresponds to a shorter drainage time. When the relative drainage rate is taken to be 3% per day, we could obtain a drainage time of two to three days for most soils.
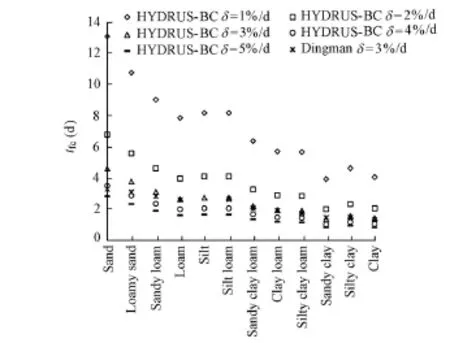
Fig. 3 Drainage time corresponding to field capacity obtained with simplified dynamic method and different values of relative drainage rate
4 Comparison of calculated field capacities of different methods
Figs. 4 and 5 show the field capacities of four soil data groups estimated with three different methods: the pressure-based method with the matric potential of −1/3 bar, the flux-based method with the drainage flux of 0.005 cm/d, and the simplified dynamic model with the relative drainage rate of 3% per day. The three methods show a similar performancefor the four soil data groups. The field capacities of the soil data group from Dingman (1994) estimated with the pressure-based method are a little larger than those of the other two methods (Fig. 4(b)). Both the flux-based method and the simplified dynamic model estimate the field capacity based on thesoil parameters Ksand c in the BC model (Eq. (7) and Eq. (9)), but the pressure-based method estimates the field capacity based on the soil parameters ψaeand b in the BC model (Eq. (5)). Therefore, it is reasonable that the result of the pressure-based method is a little difference from those of the other two methods. The cases are similar in the vG model. We can conclude that the simplified dynamic model with the relative drainage rate of 3% per day is a good choice for estimating the field capacity.
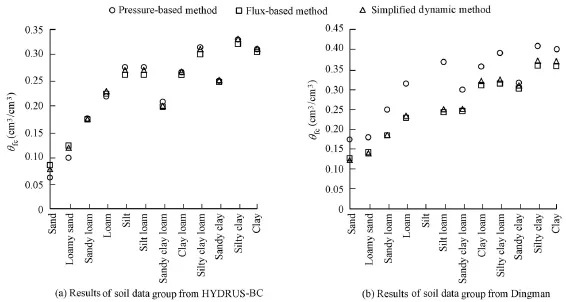
Fig. 4 Field capacity estimated with different methods based on BC model
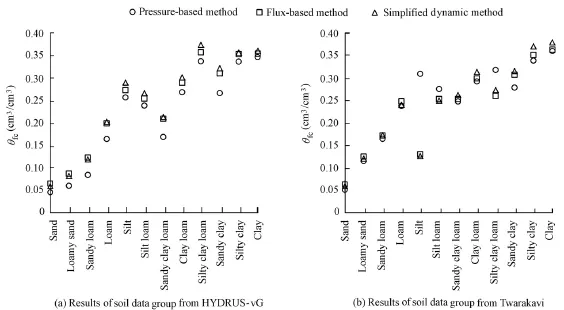
Fig. 5 Field capacity estimated with different methods based on vG model
Another parameter that can be used to estimate the field capacity is the relative soil water content. Based on the results of the simplified dynamic method, the relative water contents of different soil data groups are shown in Fig. 6. Therefore, it is acceptable to estimate the fieldcapacity as being 60% to 70% of the saturated water content for irrigated soil, such as the loam group.

Fig. 6 Relative water content corresponding to field capacity estimated with simplified dynamic method
5 Conclusions
Based on the definition of field capacity and dynamic methods of estimating field capacity, a simplified dynamic method is presented with a clearly physically-based process. This method has only one parameter independent of soil type, i.e., the relative drainage rate.
Relative drainage rates of 1%, 2%, 3%, 4%, and 5% per day were used in this simplified dynamic method to calculate the matric potential, the drainage flux, and the drainage time corresponding to the field capacity. Comparison of the calculated results with their traditional values, i.e., −1/3 bar for the matric potential, 0.005 cm/d for the drainage flux, and two to three days for the drainage time, shows that when the relative drainage rate is taken to be 3%, the simplified dynamic method can obtain matric potential, drainage flux, and drainage time values similar to the traditional values for most soils suitable for cultivating plants. Therefore, it is reasonable to use a relative drainage rate of 3% per day in the simplified dynamic method.
The three methods, i.e., the pressure-based method with a matric potential of −1/3 bar, the flux-based method with a drainage flux of 0.005 cm/d, and the simplified dynamic model with a relative drainage rate of 3% per day, show a similar performance in estimating the field capacity for most soil data groups.
While this discussion is based on theoretical analysis, it should be noted that in some cases in situ work is more useful (Zacharias and Bohne 2008). In addition, although this study used average values of each soil type in soil data groups, analysis and estimation of the field capacity based on those data can be practical.
Batjes, N. H. 1996. Development of a world data set of soil water retention properties using pedotransfer rules. Geoderma, 71(1), 31-52. [doi:10.1016/0016-7061(95)00089-5]
Brooks, R. H., and Corey, A. T. 1964. Hydraulic Properties of Porous Media. Fort Collins: Colorado StateUniversity.
Brouwer, C., Prins, K., and Heibloem, M. 1989. Irrigation Water Management: Irrigation Scheduling, Training Manual No. 4. Rome: FAO.
Campbell, G. S. 1974. A simple method for determining unsaturated conductivity from moisture retention data. Soil Science, 117(6), 311-314. [doi:10.1097/00010694-197406000-00001]
Carsel, R. F., and Parrish, R. S. 1988. Developing joint probability distributions of soil water retention characteristics. Water Resources Research, 24(5), 755-769. [doi:10.1029/WR024i005p00755]
Clapp, R. B., and Hornberger, G. M. 1978. Empirical equations for some soil hydraulic properties. Water Resources Research, 14(4), 601-604. [doi:10.1029/WR014i004p00601]
Colman, E. 1947. A laboratory procedure for determining the field capacity of soils. Soil Science, 63(4), 277-283.
Dingman, S. L. 1994. Physical Hydrology, 575. Upper Saddle River: Prentice Hall.
Hillel, D. 1998. Environmental Soil Physics: Fundamentals, Applications, and Environmental Considerations. San Diego: Academic Press.
Leij, F. J. 1996. The UNSODA Unsaturated Soil Hydraulic Database, User's Manual. National Risk Management Research Laboratory, Office of Research and Development, US Environmental Protection Agency.
Meyer, P. D., and Gee, G. W. 1999. Flux-based estimation of field capacity. Journal of Geotechnical and Geoenvironmental Engineering, 125(7), 595-599. [doi:10.1061/(ASCE)1090-0241(1999)125:7(595)]
Mualem, Y. 1976. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resources Research, 12(3), 513-522. [doi:10.1029/WR012i003p00513]
Nachabe, M. H. 1998. Refining the definition of field capacity in the literature. Journal of Irrigation and Drainage Engineering, 124(4), 230-232. [doi:10.1061/(ASCE)0733-9437(1998)124:4(230)]
Neitsch, S. L., Arnold, J. G., Kiniry, J. R., Williams, J. R., and King, K. W. 2005. Soil and Water Assessment Tool Theoretical Documentation, Version 2000. Temple: Soil and Water Research Laboratory, Agricultural Research Service.
Rawls, W. J., Brakensiek, D. L., and Saxton, K. E. 1982. Estimation of soil water properties. Transactions of the ASAE, 25(5), 1316-1320.
Richards, L. R., and Weaver, L. A. 1944. Moisture retention by some irrigated soils as related to soil moisture tension. Journal of Agricultural Research, 69(6), 215-235.
Rodríguez-Iturbe, I., and Porporato, A. 2004. Ecohydrology of Water-controlled Ecosystems: Soil Moisture and Plant Dynamics. Cambridge: Cambridge University Press.
Romano, N., and Santini, A. 2002. Water retention and storage: Field. Dane, J. H., and Topp, G. C., Eds., Methods of Soil Analysis, Part 4: Physical Methods, 721-738. Madison: Soil Science Society of America.
Schaap, M. G., Leij, F. J., and van Genuchten, M. T. 2001. Rosetta: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. Journal of Hydrology, 251(3), 163-176. [doi:10.1016/S0022-1694(01)00466-8]
Singh, V. P. 1995. Computer Models of Watershed Hydrology. Highlands Ranch: Water Resources Publications.
Sun, H. W., and Yang, J. Z. 2013. Modified numerical approach to estimate field capacity. Journal of Hydrologic Engineering, 18(4), 431-438. [doi:10.1061/(ASCE)HE.1943-5584.0000662]
Twarakavi, N. K. C., Sakai, M., and Simunek, J. 2009. An objective analysis of the dynamic nature of field capacity. Water Resources Research, 45(10), W10410. [doi:10.1029/2009WR007944]
van Genuchten, M. T. 1980. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Science Society of America Journal, 44(5), 892-898. [doi:10.2136/sssaj1980. 03615995004400050002x]
Veihmeyer, F. J., and Hendrickson, A. H. 1931. The moisture equivalent as a measure of the field capacity of soils. Soil Science, 32(3), 181-193.
Wösten, J. H. M., Lilly, A., Nemes, A., and Le Bas, C. 1999. Development and use of a database of hydraulic properties of European soils. Geoderma, 90(3), 169-185. [doi:10.1016/S0016-7061(98)00132-3]
Zacharias, S., and Bohne, K. 2008. Attempt of a flux-based evaluation of field capacity. Journal of Plant Nutrition and Soil Science, 171(3), 399-408. [doi:10.1002/jpln.200625168]
(Edited by Ye SHI)
This work was supported by the National Natural Science Foundation of China (Grants No. 51179083 and 91225302).
*Corresponding author (e-mail: congzht@tsinghua.edu.cn)
Received Nov. 11, 2013; accepted Jun. 14, 2014
 Water Science and Engineering2014年4期
Water Science and Engineering2014年4期
- Water Science and Engineering的其它文章
- Effects of reservoirs on seasonal discharge of Irtysh River measured by Lepage test
- Impact of nutrient losses from agricultural lands on nutrient stocks in Dianshan Lake in Shanghai, China
- Experimental study on desorption of soluble matter as influenced by cations in static water
- Purification and utilization of garlic processing wastewater in lotus pond wetlands
- Optimal early refill rules for Danjiangkou Reservoir
- Comparison between dynamic programming and genetic algorithm for hydro unit economic load dispatch
