Optimal early refill rules for Danjiangkou Reservoir
Yun WANG, Sheng-lian GUO*, Guang YANG, Xing-jun HONG, Ting HU
1. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China
2. China Three Gorges Corporation, Yichang 443133, China
Optimal early refill rules for Danjiangkou Reservoir
Yun WANG1, Sheng-lian GUO*1, Guang YANG1, Xing-jun HONG1, Ting HU2
1. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China
2. China Three Gorges Corporation, Yichang 443133, China
Water levels in reservoirs are generally not allowed to exceed the flood-limited water level during the flood season, which means that huge amounts of water spill in order to provide adequate storage for flood prevention and that it is difficult to fill the reservoir fully at the end of year. Early reservoir refill is an effective method for addressing the contradiction between the needs of flood control and of comprehensive utilization. This study selected the Danjiangkou Reservoir, which is the water source for the middle route of the South-North Water Diversion Project (SNWDP) in China, as a case study, and analyzed the necessity and operational feasibility of early reservoir refill. An early reservoir refill model is proposed based on the maximum average storage ratio, optimized by the progressive optimality algorithm, and the optimal scheduling schemes were obtained. Results show that the best time of refill operation for the Danjiangkou Reservoir is September 15, and the upper limit water level during September is 166 m. The proposed early refill scheme, in stages, can increase the annual average storage ratio from 77.51% to 81.99%, and decrease spilled water from 2.439 × 109m3to 1.692 × 109m3, in comparison to the original design scheme. The suggested early reservoir refill scheme can be easily operated with significant comprehensive benefits, which may provide a good reference for scheduling decision-making.
reservoir operation; early reservoir refill; operation rules in stages; progressive optimality algorithm; Danjiangkou Reservoir
1 Introduction
Reservoir operation aims at redistributing water resources, minimizing risks and consequences of water shortages and floods, and maximizing water utilization efficiency with the guidelines of operation rules. Therefore, deriving effective operation rules is essential, as they have a direct impact on a reservoir’s comprehensive benefits (Liu et al. 2006; Liu et al. 2011).
Operating rules address the relationships among optimal release series, reservoir state variables and hydrological inputs such as storage and inflows (Bhaskar and Whitlatch 1980). Generally, operating rules are predefined at the planning stage of reservoir construction andpresented in various forms, such as operation functions, operation curves and tables. Most of them are evaluated by simulation models (Ngo et al. 2007), which have been developed widely for managing reservoir systems over last few decades (Palmer et al. 1980; Schuster 1987; Wurbs 1993). Although operating rules have become very efficient over time, it is necessary to modify the existing rules when new facilities are installed or the reservoir’s demands and objectives change (Oliveira and Loucks 1997). An effective approach combining optimization models with simulation models to derive operating rules was proposed to solve such problems (Simonovic 1992; Koutsoyiannis and Economou 2003; Celeste and Billib 2009; Rani and Moreira 2010; Guo et al. 2011). From these studies, simulation models were used to verify and analyze the performance of a reservoir under changing conditions, and optimization models were applied to determine the best sequences of releases (Liu et al. 2006).
Due to the high-dimensional, nonlinear, and stochastic characteristics of reservoir systems, lots of optimization algorithms have been used in reservoir operation, including dynamic programming (DP), genetic algorithms (GAs), artificial neural networks (ANNs), and particle swarm optimization (PSO). Compared with these optimization techniques, the progressive optimality algorithm (POA) has an obvious advantage in reducing dimensionality difficulties for multi-state decision problems. With the advantages of computational efficiency and minimal storage requirements (Howson and Sancho 1975), POA has been successfully applied in water resources management (Turgeon 1981; Nanda et al. 1986; Xie et al.2012; Chen et al. 2013).
Since Clark (1956) proposed the New York City (NYC) rule, operating rules have been developed in the reservoir refill field. Bower et al. (1966) proposed the space rule, as a special case of the NYC rule, which tried to leave more space in reservoirs where greater inflows are expected. Wu (1988) explored a rule that equalizes the probability of each reservoir being empty at the end of the drawdown season. Lund and Guzman (1999) developed the linear programming NYC rule, which has the ability to incorporate other linear operating constraints in the setting of short-term storage targets for each reservoir and can also incorporate other operating purposes in the objective function. Paredes and Lund (2006) presented two operating rules for the refill and drawdown seasons of reservoirs in parallel for the water supply, considering water quality. Liu et al. (2006) proposed the dynamic programming neural-network simplex (DPNS) model to derive refill operating rules for the Three Gorges Reservoir. Results showed that the optimal operating rules performed more effectively than the design rule curves. Liu et al. (2011) proposed a simulation-optimization test framework to derive the optimal refill rule curves for a multi-objective reservoir. Results indicated that the full refill probability can be improved greatly without decreasing the flood control standard and navigation probability during the refill period. Huo et al. (2011) proposed a scheme of reservoir impoundment in late September instead of early October based on the regularity in the occurrence time of the last flood of each year for the Danjiangkou Reservoir. Resultssuggested that the scheme could maintain the original flood control standard without increasing any flood risk, and be more economically beneficial than the original one. Li et al. (2013) proposed different schemes of impounding water in advance on the basis of an optimal operation and experimental water impoundment scheme for the Three Gorges Reservoir. Results showed that the best scheme was to impound water from 145 m on September 1 to 160 m on September 30 through a continuous and uniform process, which can generate 2.47 × 109kW·h extra hydropower and save 2.53 × 109m3of flood water as compared with the original scheme.
Although intensive research has proven that the economic benefits of reservoir systems can be significantly increased through optimal operating rules, researchers such as Yeh (1985) and Panuwat et al. (2009) have realized that a gap still exists between the theoretical model and practical operation. Labadie (2004) analyzed possible reasons, including that many reservoir operators are skeptical about models’ results replacing their judgment and feel more comfortable using predefined operating rules, which are easy to comprehend and operate. Besides, many optimization models are not conducive to incorporating risk and uncertainty, which makes it difficult for reservoir managers who bear responsibility for the failure of reservoir operation to achieve optimal results. Thus, it is necessary to design operating rules with characteristics of simplicity, convenience, and strong operability, and there is a need for reservoir operators who easily accept and apply them in practical operation.
Meanwhile, there is a conflict between flood control and comprehensive utilization for most multi-purpose reservoirs. During flood seasons, reservoir water levels generally are not allowed to exceed the flood-limited water level in order to offer adequate storage for flood control, according to the Chinese Flood Control Act (Li et al. 2010). During the refill period, reservoir water levels are needed to achieve the normal water level for hydropower generation, water supply, and irrigation. If inflow is plentiful, there is no problem in achieving reservoir operation goals. However, huge amounts of water are spilled at the end of the flood period because of the limitation of the flood-limited water level, which makes it difficult for the reservoir to meet the storage target and results in low water resources utilization and economic benefits. An effective method of solving the conflict between the goals of flood control and comprehensive utilization is to implement early reservoir refill.
The aims of this study were to build an early reservoir refill model and derive optimal refill rules. The Danjiangkou Reservoir was selected as case study and the necessity and operational feasibility of early refill were analyzed. An early reservoir refill model is proposed under the constraints that it cannot reduce flood control standards. The best time of refill and the optimal operating rule were obtained based on the optimization-simulation test procedures. The performance of proposed early refill schemes is compared with the original design scheme.
2 Danjiangkou Reservoir operating rules
As shown in Fig. 1, the Danjiangkou Reservoir is located in the middle reach of the Hanjiang River, which is the largest tributary of the Yangtze River. The drainage area of thereservoir basin is 96 000 km2. The Danjiangkou Reservoir was built in 1958 and began operation in 1973, and has many engineering functions, including flood control, water supply, power generation, and navigation.

Fig. 1 Location of Danjiangkou Reservoir in Hanjiang River Basin
The Hanjiang River Basin lies in the southeast monsoon zone, dominated by cyclonic rain. In summer, this area is often threatened by heavy rain or rainstorms because of the influence of the western Pacific subtropical high and the India-Myanmar low. In autumn, the northern cold forces increase. Due to the mountainous regions above the Danjiangkou Reservoir, the cold air is blocked and stagnated for a period, which results in a rainfall peak in September and October. Therefore, the entire flood season can be divided into multiple sub-seasons through analysis of the rain-producing system of the Hanjiang River Basin. According to the Danjiangkou Water Conservancy Reservoir Operation Guidelines (CWRC 2012a), the flood season starts on June 21 and ends on October 10, with the period between June 21 and August 20 being the summer flood season and the period between September 1 and October 10 being the autumn flood reason.
2.1 Danjiangkou Reservoir extension project
The Danjiangkou Reservoir is the water source of the middle route of the South-North Water Diversion Project (SNWDP), which diverts water via new canals near the west edge of the Huang-Huai-Hai Plain to Beijing and Tianjin municipalities. The reservoir dam has been heightened since 2005. The normal water level has been raised from 157 to 170 m, and the corresponding storage capacity enlarged from 17.45 × 109to 29.05 × 109m3. The flood-limited water levels in summer and autumn are 160 m and 163.5 m, respectively. The Danjiangkou Reservoir extension project was completed in May 2013. The reservoir area has been extended by another 324 km2, affecting more than 250 000 people in Shiyan City in Hubei Province, and Xichuan County in Henan Province. The expanded Danjiangkou Reservoir will provide 9.5 × 109m3of water annually to Beijing and Tianjin municipalities, and some cities in Hebei, Henan, and Hubei provinces. It will be able to provide 13 × 109to 14 × 109m3of water by2030. The design water discharge and maximum discharge are 350 m3/s and 420 m3/s, respectively. Therefore, sufficient water in the Danjiangkou Reservoir is the primary guarantee of the middle route of the SNWDP.
2.2 Flood control operating rules
The Danjiangkou Reservoir employs a compensation scheduling mode to implement flood control. When the interval basin inflow from the Danjiangkou dam site to the Nianpanshan Hydrological Station is taken into consideration, reservoir outflow discharges are determined by subtracting interval basin inflow from the safety discharge of the Nianpanshan Hydrological Station. The flood control rules are as follows (CWRC 2012a):
(1) If the inflow is equal to or less than a 10-year flood, the safety discharge of the Nianpanshan Hydrological Station is 12 000 m3/s.
(2) If the inflow is more than a 10-year flood but does not exceed a 20-year flood, the safety discharge of the Nianpanshan Hydrological Station is 17 000 m3/s.
(3) If the inflow is greater than a 20-year flood but does not exceed a 100-year flood, the safety discharge of the Nianpanshan Hydrological Station is 21 000 m3/s.
(4) If the inflow is more than a 100-year flood but does not exceed a 10 000-year flood, the safety of downstream areas cannot be considered and the reservoir outflow discharge should be increased step-by-step according to the rising tendency of the forecasted inflow and water level. If the inflow is greater than a 10 000-year flood, the reservoir outflow discharge is equal to the maximum discharge capacity so as to guarantee the dam safety.
2.3 Original design rule curves
Original design rule curves of the Danjiangkou Reservoir are shown in Fig. 2, in which the water level is kept at 160 m (the flood-limited water level during summer) from June 21 to August 20. From August 21 to September 1, the water level is raised to 163.5 m (the flood-limited water level during autumn). Until October 10, the water level is raised gradually to the normal water level of 170 m. The water level should be kept at 170 m, as high as possible, in order to supply water until the end of next April. The water level is drawn down gradually to 160 m until June 21.

Fig. 2 Original design rule curves of Danjiangkou Reservoir
2.4 Operational necessity of early refill
Before the dam is heightened, if the reservoir refill operation is implemented according to original design rule curves, the full refill probability of the Danjiangkou Reservoir is only about 23% (Hu et al. 1991). After the dam is heightened, the reservoir storage capacity more than doubles. If the refill operating rule and starting time are still based on the original design scheme, the full refill probability of the reservoir will be significantly reduced. Moreover, Chen et al. (2007) used linear regression and Mann-Kendall methods to test long-term trends of the Danjiangkou Reservoir inflow. Their results show that at the confidence level α= 0.05 the annual runoff has a significant downward trend in the period from 1953 to 2003. If successive dry years occur and the reservoir is maintained a low water level, the available water for the receiving areas of the middle route of the SNWDP will be seriously insufficient. Hence, it is vital to implement Danjiangkou Reservoir early refill and derive optimal refill rules.
3 Operational feasibility of early refill
3.1 Statistical analysis of precipitation during flood season
Due to the influence of the monsoon climate, the annual precipitation in the Danjiangkou Reservoir Basin has dramatic diversity and uneven distribution. The average annual precipitation is about 700 to 1 100 mm. The maximum observed annual precipitation, which occurred in 1964, was 1 360 mm, and the minimum observed annual precipitation, which occurred in 1978, was only 504 mm. Rainstorms occur frequently in the period from July to October. Based on daily rainfall data during the flood season from 1954 to 2011, the annual average precipitation amounts of a ten-day period are listed in Table 1. It can found that the precipitation in July is the heaviest. In middle and late September, average rainfall begins to decrease significantly, which causes flood control pressure to be relatively lower. It is feasible to start to implement early refill for the Danjiangkou Reservoir in the middle of September from the annual rainfall distribution prediction.
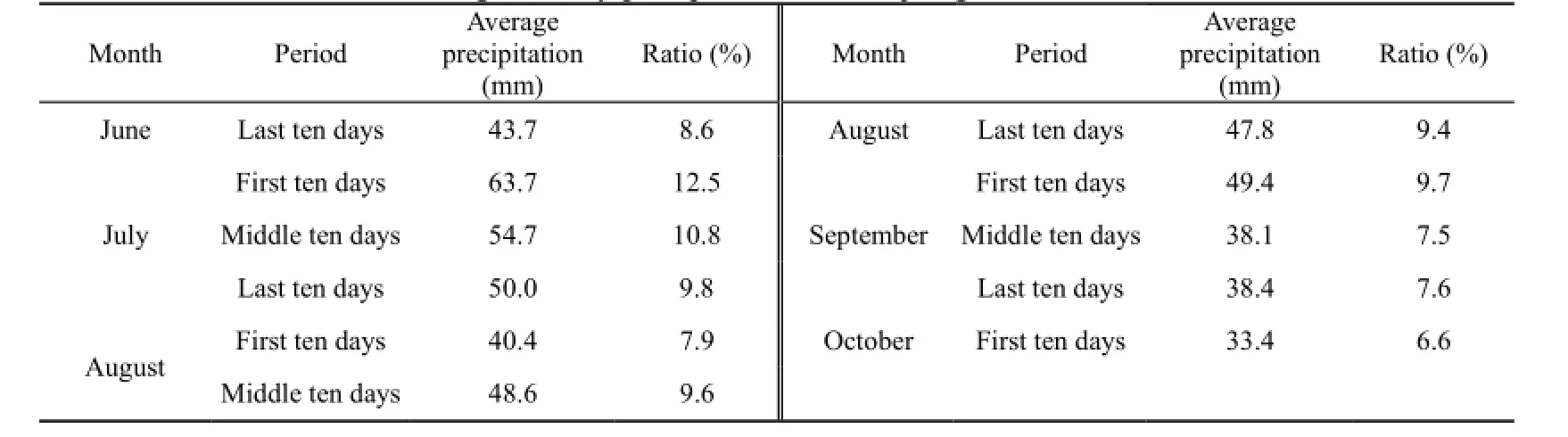
Table 1 Statistics of average ten-day precipitation for Danjiangkou Reservoir from 1954 to 2011
3.2 Reservoir inflow analysis for September
The monthly average inflow for the Danjiangkou Reservoir in September from 1954 to2011 is shown in Fig. 3, with theaverage inflow in September being 2 440 m3/s. The maximum observed monthly averageflow was 9 013 m3/s and occurred in 1964, while the minimum observed monthly average flow was 217 m3/s and occurred in 1999. Fig. 3 demonstrates that the inflow in September has a significant inter-annual fluctuation. If the operation water level of the reservoir in September is controlled uniformly by the autumn flood-limited water level, too much water will be spilled and water resources utilization efficiency will be reduced greatly. With five days selected as a time interval, the probabilities of flooding during September in each period were analyzed and are listed in Table 2. It can be seen that the probability of a large flood occurring is extremely low. During middle and late September, the frequency of a number of medium and small floods decreases, and the large peak discharge tends to drop off over time. This can create the conditions for the Danjiangkou Reservoir early refill operation.

Fig. 3 Average monthly inflow in September from 1954 to 2011

Table 2 Statistics of flood peaks in September for Danjiangkou Reservoir
3.3 Reservoir flood control capacity analysis
Many water conservancy projects have been built upstream of the Danjiangkou Reservoir Basin in the last three years, including the Shimen, Shiquan, Pankou, Ankang, Linhekou, and Huanglongtan reservoirs. The total flood prevention storage capacity of these upstream reservoirs is about 1.06 × 109m3, which has greatly reduced the flood control pressuredownstream. After the Danjiangkou Reservoir extension project was finished, the reserved flood prevention storage capacity was enlarged from a range of 55 × 109to 77.2 × 109m3to a range of 81.2 × 109to 110× 109m3, and the flood control standards of the middle and lower reaches of the Hanjiang River have been enhanced from 20-year to 100-year return periods.
In addition, the administration bureau of the Danjiangkou Reservoir has strong technical capabilities, including its hydrological information-collecting and dispatching automation system, and professional meteorological forecasting system. The developed flood forecasting models have extended the effective lead-time significantly and provided relatively high accuracy (Chau et al. 2005; Wu et al. 2009; Taormina et al. 2012). All of these favorable conditions will provide technical support for the Danjiangkou Reservoir early refill operation.
4 Early reservoir refill operation
4.1 Early refill operating rules
Assuming that the start of the refill period is advanced to September 10, the refill guide curve of the Danjiangkou Reservoir is shown in Fig. 4. The early reservoir refill is guided by the upper limited water level (ULWL) and the refill guide curve. The early refill operating rules can be described as follows:

Fig. 4 Scheduling graph of early refill for Danjiangkou Reservoir
(1) When the water level is below the refill guide curve (Zone III), the reservoir releases the minimum discharge determined by comprehensive utilization.
(2) When the water level is between the ULWL and the refill guide curve (Zone II) before October, the water level is guided by the refill guide curve if no flood occurs. If a medium or small flood (equal to or smaller than a 20-year flood) occurs, the maximum outflow discharge should not exceed 17 000 m3/s and the highest water level is kept below the ULWL. After October, the operating rule is same, but the ULWL is replaced by the normal water level.
(3) When the water level is higher than the ULWL (Zone I) and a 1 000-year seasonal design flood occurs simultaneously, the highest flood water level must be kept less than the design flood level of 172.2 m. Meanwhile, the artificial flood peak phenomenon, which iswhen the outflow is greater than the inflow, cannot occur during the process of flood control.
Due to the stochastic characteristics of floods, various flood control projects and facilities are designed based on annual flood frequency analysis. For example, the flood prevention storage capacity of a reservoir will not be used fully for most of hydrological years when the peak discharge is less than a 1 000-year design flood. These features result in a huge amount of flood water being spilled during flood seasons, and insufficient water being refilled during the refill period. To overcome these drawbacks, a method of dividing the flood prevention storage capacity into two parts with the ULWL is proposed. The whole storage capacity is used to regulate 1 000-year seasonal design floods, while the storage capacity below the ULWL is used to regulate medium and small floods. In such a way, early reservoir refill operation is conducted when the forecasting inflow discharge is smaller than the 20-year design flood. Otherwise the reservoir is operated based on design flood control rules (Liu et al. 2011).
4.2 Early refill operation model
Based on these operating rules, an early reservoir refill operation model is proposed. The value of ULWL and the water level of each node in the refill guide curve can be obtained by the optimization-simulation test approach. The objective function is as follows:

Constraints:
(1) Water balance equation:
(2) Reservoir water level limits:
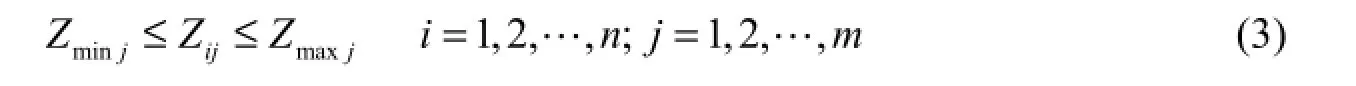
(3) Power generation limits:
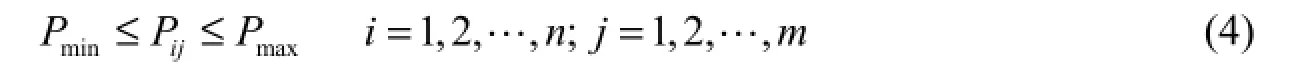
(4) Reservoir discharge limits:
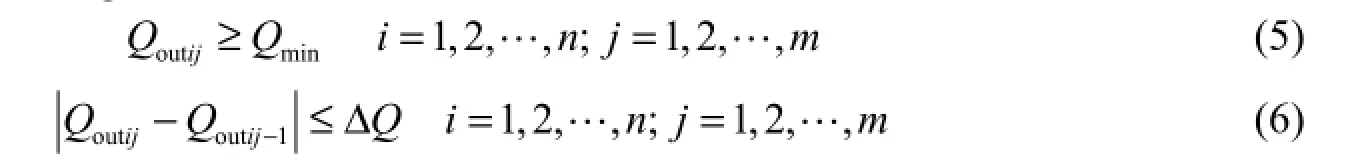
where Rfis the annual average storage ratio, denoting the extent of reservoir refill (%); n is the number of years; i denotes the sequence number of years; m is the length of the new refill period in days; j denotes the sequence number of days; Vhighiis the reservoir storage of the highest water level in the ith year (m3); Vminis the reservoir storage of the dead water level (m3); Vmaxis the reservoir storage of the normal pool water level (m3); Vijis the reservoir storage on the jth day of the refill period in the ith year (m3); Qinijis the reservoir inflow on the jth day of the refill period in the ith year (m3/s); Qoutijis the reservoir discharge on the jth day of the refill period in the ith year (m3/s); Δt is the time step; Zijis the water level on the jthday of the refill period in the ith year (m); Zminjis the minimum water level of the reservoir on the jth day of the refill period (m); Zmaxjis the maximum water level of the reservoir on the jth day of the refill period (m); Pijis the output power on the jth day of the refill period in the ith year (kW); Pminis the minimum power limit of the reservoir (kW); Pmaxis the maximum power limit of the reservoir (kW); Qminis the minimum flow discharge for downstream comprehensive utilization (m3/s); and ΔQ is the maximum release flow fluctuation of reservoir (m3/s).
4.3 Solution algorithm
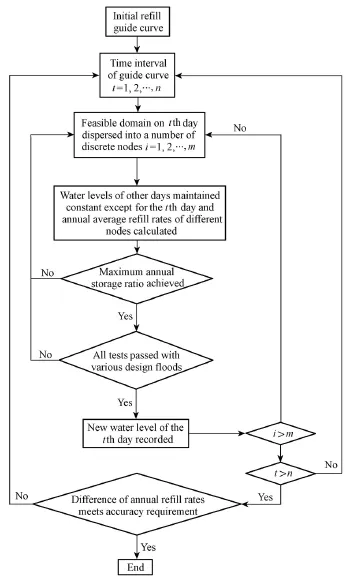
Fig. 5 Calculation flow chart of early refill operation model
The early refill model mainly consists of three modules: optimization, simulation, and a design flood test. The calculation procedures and flow chart are shown in Fig. 5. For the optimization module, the POA is used to optimize the water level of each day in the refill guide curve, and the best one/ones are chosen by maximizing the annual average storage ratiovalue. The discrete step in the POA is equal to 0.1 m. In the simulation module, the observed flow data series is simulated by proposed refill operating rules, and the evaluation indexes, such as annual average spilled water, are calculated. In the design flood test module, whether the obtained solutions can reduce the downstream flood control pressure for medium and small floods and ensure the safety of the reservoir and downstream area during large floods are tested. The test standards hold that the water level cannot exceed the design water level when the 1 000-year autumn design flood occurs and the water level cannot exceed the normal water level when the 20-year autumn design flood occurs. The rule curves have an impact on flood routing, and it is necessary to test their feasibility for flood control safety after optimization each time. Testing of the design flood can help to obtain feasible solutions, and the optimal ones can be obtained through loops of the optimization-simulation test. In this way, a test of design flood routing is integrated into the optimization for comprehensive utilization benefits. The ULWL can be determined by a combination of design flood routing and optimization techniques, achieving a best balance between flood control and comprehensive utilization benefits.
5 Results and discussion
5.1 Optimal scheduling results
Based on these operational feasibilities of early refill for the Danjiangkou Reservoir, advancing the early refill time to the middle of September is reasonable. Assuming that September 10, September 15, September 20, and September 25 are the start times, different refill periods from the start time to December 31 were calculated. The typical flow hydrograph of 1964 during the refill period was selected, and the peak-amplitude method that has been reviewed and discussed in detail by Xiao et al. (2009) was used to derive 10-year, 20-year, 100-year, and 1 000-year autumn design flood hydrographs. The early refill operation model was employed to simulate reservoir scheduling with daily inflow data from 1954 to 2011. Table 3 lists reservoir scheduling results with different early refill schemes. The highest water level and the time that the reservoir was refilled fully in the typical year of 1964 are also listed in Table 3.
Of all optimal schemes, the scheme that starts on September 15 with the value of ULWL equal to 166 m performs best. Table 3 shows that the number of years of the reservoir being refilled fully and the annual average storage ratio are 12 years and 81.91%, respectively. The optimal scheduling graph of the Danjiangkou Reservoir is shown in Fig. 6, in which the slope of the refill guide curve appears to have a decreasing trend before October 1. Since the inflow in the middle of September is relatively small, as shown in Tables 1 and 2, the refill guide curve can rise quickly to maximum comprehensive utilization benefits without increasing flood control risks. The refill guide curve increases slowly in late September in order to guarantee that the water level on October 1 is below 166 m (ULWL). During the period betweenOctober 1 and October 6, the probability of flooding is high in this basin, the reservoir has to reserve more storage capacity for flood prevention, and the refill guide curve rises slowly. Afterwards, the probability of flooding is significantly reduced, the flood control pressure decreases, and the refill guide curve rises quickly to reach the normal water level of 170 m.
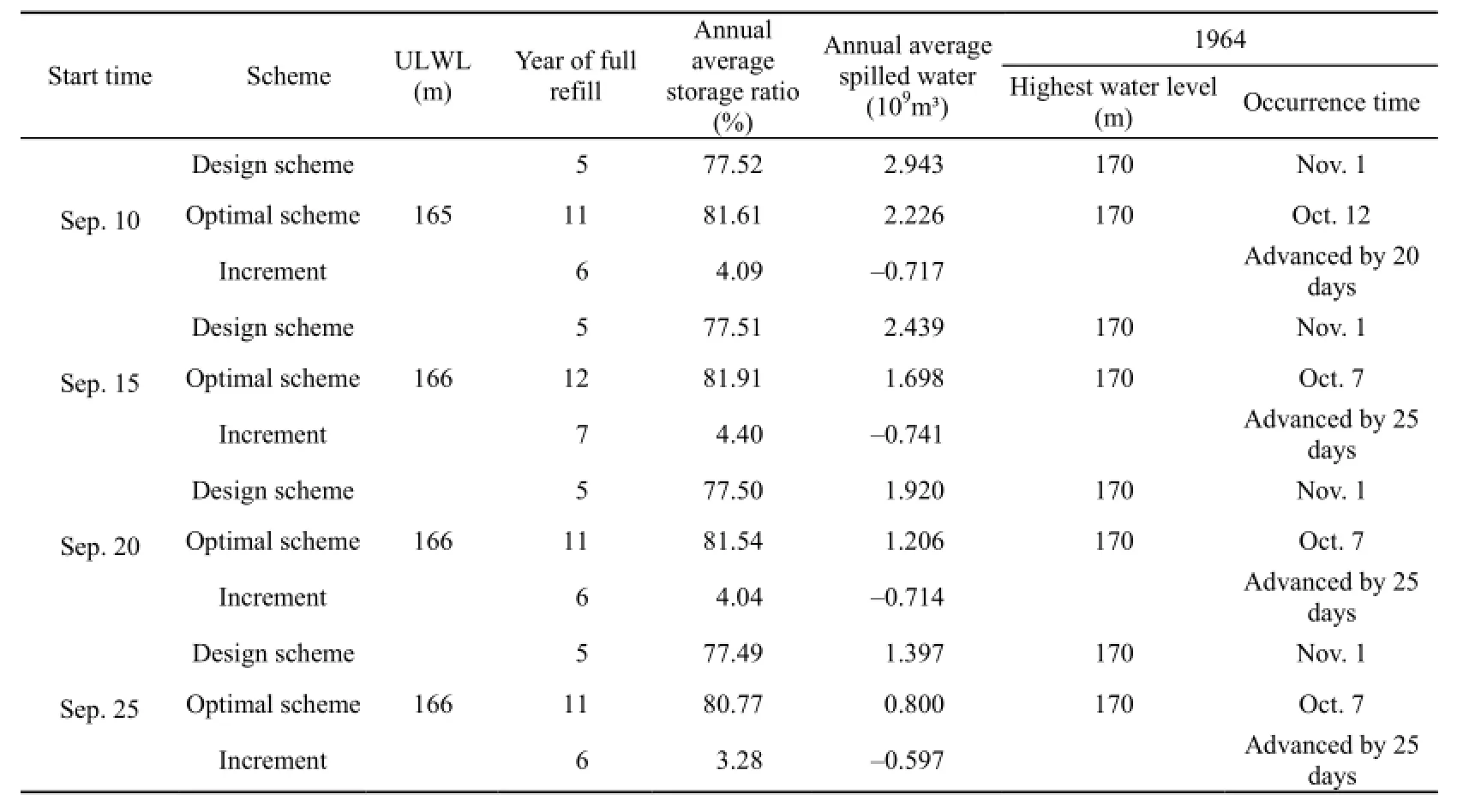
Table 3 Results of different early refill operation schemes
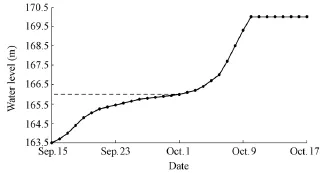
Fig. 6 Optimal scheduling graph for Danjiangkou Reservoir
5.2 Early refill in stages
According to this early refill operation model, the optimal scheduling scheme has been obtained. This model assumes that the water level at any time in September cannot exceed ULWL. The disadvantage of this assumption is that if the inflow is large, the water level reaches ULWL quickly and the reserved flood prevention storage capacity becomes smaller in the middle of September, which might cause the adverse impact of subsequent flood control operation in late September. Therefore, the scheme of early refill in stages is suggested to ensure flood control safety in September. On the basis of the optimal scheduling scheme, the best start time of refill is September 15 and the value of ULWL is 166 m. A five-day time interval was selected to divide the early refill period into four stages, which are listed in Table 4.

Table 4 Different schemes of early refill in stages
All of these schemes in Table 4 were simulated with the early refill operation model. The results indicate that scheme 9 to scheme 15 are unreasonable because the highest water levels in the early refill period exceeded 166 m (ULWL) when the 20-year autumn design flood occurred. This is contrary to the operating rule that the highest water level must be kept below ULWL when the medium and small floods (equal to or smaller than a 20-year design flood) occur. Therefore, only the results of the first eight schemes are listed in Table 5, in which the water utilization efficiency of scheme 8 is the highest. Compared with the original design scheme, the year of the reservoir being refilled fully in scheme 8 increased from 5 years to 12 years and its annual average storage ratio increased from 77.51% to 81.99%. The average annual amount of spilled water was 1.692 × 109m3, which is reduced by 0.747 × 109m3. The time that the reservoir was refilled fully was advanced by 25 days. As a result, it is suggested that the Danjiangkou Reservoir begin to refill on September 15 from the flood-limited water level (163.5 m) and that the water level does not exceed 164.5 m from September 16 to September 20, does not exceed 165 m from September 21 to September 25, does not exceed165.5 m from September 26 to September 30, and does not exceed 166 m on October 1.
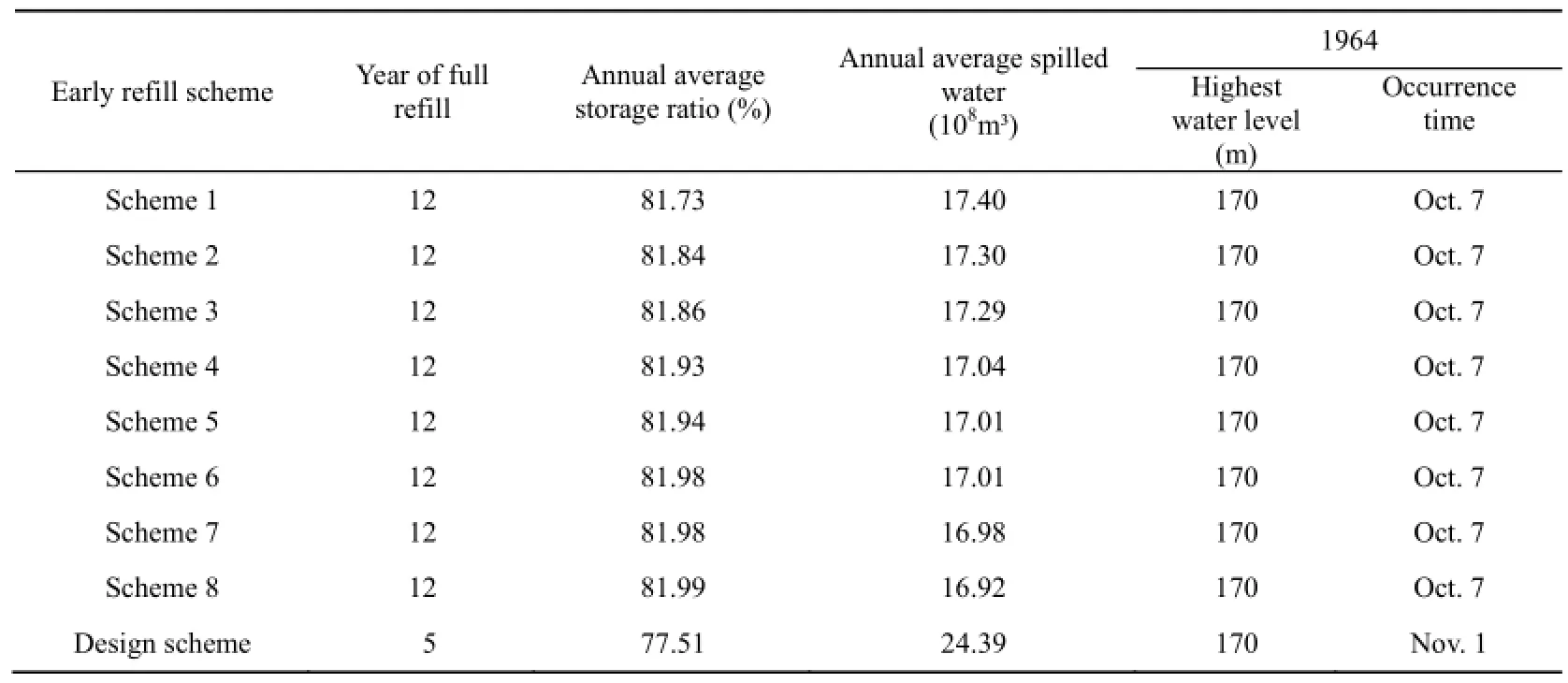
Table 5 Results of different schemes of early refill in stages
5.3 Flood control safety analysis
The 10-year, 20-year, 100-year, and 1 000-year autumn design floods were used to test the flood control safety of the optimal scheme and schemes of early refill in stages, respectively. Table 6 shows that, for the downstream flood control requirements, all maximum outflow discharges do not exceed the safety discharge when a 100-year-or-smaller flood occurs. As for flood control requirements of the reservoir, when a 20-year-or-smaller design flood occurs, the highest water levels in September and the refill period are below ULWL (166 m) and the normal water level (170 m), respectively. This demonstrates that the refill guide curve and ULWL can control medium and small floods effectively. When 100-year and 1 000-year design floods occur, the highest water levels during the early refill period exceed 166 m. This is because the inflow is large and, if the water level is still strictly guided by the refill guide curve, the outflow will exceed the downstream safety discharge. In order to guarantee downstream safety, the reservoir has to be operated according to the rule in Zone I (Fig. 4), and the water level rises but does not exceed the design flood level 172.2 m, so reservoir safety can still be ensured by both schemes. When the optimal scheme is compared with the scheme of early refill in stages, the highest water level of the former is slightly larger than the latter, which implies that the scheme of early refill in stages is much better for flood control operation.

Table 6 Comparison of two early refill schemes with different design floods
5.4 Early refill scheduling process in 1983
The largest autumn flood, corresponding to a 20-year autumn flood, was observed on October 5, 1983 in the Danjiangkou Reservoir Basin. Fig. 7 shows a scheduling process simulated by the scheme of early refill in stages, in which the water level in September was effectively controlled by the refill guide curve. After the flood peak occurred, the reservoir water level quickly rose to 170 m. For this flood event, the maximum outflow discharge was 13 900 m3/s, which did not exceed the safety discharge of the downstream area (17 000 m3/s). Fig. 7 shows that the scheme of early refill in stages can control medium and small floods effectively and maximize the reservoir comprehensive utilization benefits without reducing the flood prevention standard.

Fig. 7 Early refill scheduling process in 1983
6 Conclusions
The low refill probability of the Danjiangkou Reservoir has an adverse impact on the reservoir comprehensive utilization benefits. Since the dam was heightened, the storage capacity has more than doubled and the problem of the reservoir’s incapability of being refilled has become more prominent. The operational feasibility of reservoir early refill was analyzed in terms of precipitation, inflow discharge, and reservoir flood control capacity. The early reservoir refill operation model was proposed and optimized using daily inflow data from 1954 to 2011. The 10-year, 20-year, 100-year, and 1 000-year autumn design floods were used to test flood control safety for all early refill schemes. The main conclusions of this study are as follows:
(1) The necessity and feasibility of early refill operation for the Danjiangkou Reservoir have been demonstrated. It is recommended that the best time to start early refill operation is September 15, and the value of the upper limit water level during September is 166 m.
(2) The best scheme of early refill in stages maintains the water level at or below 164.5 m from September 16 to September 20, at or below 165 m from September 21 to September 25, at or below 165.5 m from September 26 to September 30, and at or below 166 m on October 1.
(3) When the best scheme of early refill in stages is compared with the original design scheme, the annual average storage ratio is increased from 77.51% to 81.99%, and the annually spilled water is reduced by 0.747 × 109m3. The occurrence of the reservoir being refilled fully is advanced by 25 days.
The proposed scheme not only maximizes the reservoir comprehensive utilization benefits without reducing flood prevention standards, but also provides a good reference for reservoir scheduling decision making. In addition, the operational ease and safety make it possible for reservoir managers to accept optimal results and put the scheme into wide practice. However, this study does not consider flood forecasting. Combining real-time flood forecasting with early reservoir refill will be a part of our future research.
Bhaskar, N. R., and Whitlatch, E. E. 1980. Derivation of monthly reservoir release policies. Water ResourcesResearch, 16(6), 987-993.
Bower, B. T., Hufschmidt, M. M., and Reedy, W. W. 1966. Operating Procedures: Their Role in the Design of Water-Resource Systems by Simulation Analyses. Cambridge: Harvard University Press.
Celeste, A. B., and Billib, M. 2009. Evaluation of stochastic reservoir operation optimization models. Advances in Water Resources, 32(9), 1429-1443. [doi:10.1016/j.advwatres.2009.06.008]
Changjiang Water Resources Commission (CWRC). 2012a. Danjiangkou Water Conservancy Reservoir Operation Guidelines. Dankou: Administration Bureau of Danjiangkou Reservoir Press.
Changjiang Water Resources Commission (CWRC). 2012b. The Design Flood and Operation Guideline for the Danjiangkou Reservoir. Dankou: Administration Bureau of Danjiangkou Reservoir Press.
Chau, K. W., Wu, C. L., and Li, Y. S. 2005. Comparison of several flood forecasting models in Yangtze River. Journal of Hydrologic Engineering, 10(6), 485-491. [doi:10.1061/(ASCE)1084-0699(2005)10:6(485)]
Chen, H., Guo, S. L., Xu, C. Y., and Singh, V. P. 2007. Historical temporal trends of hydro-climatic variables and runoff response to climate variability and their relevance in water resource management in the Hanjiang basin. Journal of Hydrology, 344(3-4), 171-184. [doi:10.1016/j.jhydrol.2007.06.034]
Chen, J. H., Guo, S. L., Li, Y., Liu, P., and Zhou, Y. L. 2013. Joint operation and dynamic control of flood limiting water levels for cascade reservoirs. Water Resources Management, 27(3), 749-763. [doi:10.1007/s11269-012-0213-z]
Clark, E. J. 1956. Impounding reservoirs. Journal of the American Water Works Association, 48(4), 349-354.
Guo, S. L., Chen, J. H., Li, Y., Liu, P., and Li, T. Y. 2011. Joint operation of the multi-reservoir system of the Three Gorges and the Qingjiang cascade reservoirs. Energies, 4(7), 1036-1050. [doi:10.3390/en4071036]
Howson, H. R., and Sancho, N. G. F. 1975. A new algorithm for the solution of multi-state dynamic programming problems. Math Program, 8(1), 104-116.
Huo, J. J, Xu, J. J, and Zhang, L. L. 2011. Impoundment in advance at the end of flood season for danjiangkou reservoir. Journal of Yangtze River Scientific Research Institute, 28(12), 68-71. (in Chinese).
Hu, Z. P., Feng, S. Y., and Yu, F. Q. 1991. Strategy of flood control water level for Danjiangkou reservoir. Water Resources and Hydropower Engineering, 11, 1-7. (in Chinese).
Koutsoyiannis, D., and Economou, A. 2003. Evaluation of the parameterization-simulation-optimization approach for the control of reservoir systems. Water Resources Research, 39(6), 1-17. [doi:10.1029/2003WR002148]
Labadie, J. 2004. Optimal operation of multireservoir systems: State-of-the-art review. Journal of Water Resources Planning and Management, 130(2), 93-111. [doi:10.1061/(ASCE)0733-9496(2004)130:2(93)]
Li, X., Guo, S. L., Liu, P., and Chen, G. Y. 2010. Dynamic control of flood limited water level for reservoir operation by considering inflow uncertainty. Journal of Hydrology, 391(1-2), 124-132. [doi:10.1016/j.jhydrol.2010.07.011]
Li, Y., Guo, S. L., Guo, H. J., Zhang, H. G., and Ding, S. X. 2013. Flood control risk and benefit of impounding water in advance for the Three Gorges Reservoir. Journal of Yangtze River Scientific Research Institute, 30(1), 8-14. (in Chinese).
Liu, P., Guo, S. L., Xiong, L. H., Li, W., and Zhang, H. G. 2006. Deriving reservoir refill operating rules by using the proposed DPNS model. Water Resources Management, 20(3), 337-357. [doi:10.1007/ s11269-006-0322-7]
Liu, X. Y., Guo, S. L., Liu, P., Chen, L., and Li, X. 2011. Deriving optimal refill rules for multi-purpose reservoir operation. Water Resources Management, 25(2), 431-448. [doi:10.1007/s11269-010-9707-8]
Lund, J. R., and Guzman, J. 1999. Derived operating rules for reservoirs in series or in parallel. Journal of Water Resources Planning and Management, 125(3), 143-153. [doi:10.1061/(ASCE)0733-9496 (1999)125:3(143)]
Nanda, J., Bijwa, P. R., and Kothari, D. P. 1986. Application of progressive optimality algorithm to optimal hydrothermal scheduling considering dererministic and stochastic data. Electrical Power and Energy Systems, 8(1), 61-64. [doi:10.1016/0142-0615 (86)90026-8]
Ngo, L. L., Madsen, H., and Rosbjerg, D. 2007. Simulation and optimization modeling approach for operation of the Hoa Binh reservoir, Vietnam. Journal of Hydrology, 336(3-4), 269-281. [doi:10.1016/j.jhydrol.2007.01.003]
Oliveira, R., and Loucks, D. P. 1997. Operating rules for multireservoir systems. Water Resources Research, 33(4), 839-852. [doi:10.1029/96WR03745]
Palmer, R. N., Wright, J. R., Smith, J. A., Cohon, J. L., and ReVelle, C. S. 1980. Policy Analysis of Reservoir Operation in the Potomac River Basin, Volume I, Executive Summary. Baltimore: Johns Hopkins University.
Panuwat, P., Ashim, D. G., Mukand, S. B., and Sutat, W. 2009. Improved reservoir operation using hybrid genetic algorithm and neurofuzzy computing. Water Resources Management, 23(4), 697-720. [doi:10.1007/s11269-008-9295-z]
Paredes, J., and Lund, J. R. 2006. Refill and drawdown rules for parallel reservoirs: Quantity and quality. Water Resources Management, 20(3), 359-376. [doi:10.1007/s11269-006-0325-4]
Rani, D., and Moreira, M. M. 2010. Simulation-optimization modeling: A survey and potential application in reservoir systems operation. Water Resources Management, 24(6), 1107-1138. [doi:10.1007/ s11269-009-9488-0]
Schuster, R. J. 1987. Colorado River Simulation System, Executive Summary. Denver: U.S. Bureau of Reclamation, Engineering and Research Center.
Simonovic, S. 1992. Reservoir system analysis: Closing gap between theory and practice. Journal of Water Resources Planning and Management, 118(3), 262-280. [doi:10.1061/(ASCE) 0733-9496(1992)118:3(262)]
Taormina, R., Chau, K. W., and Sethi, R. 2012. Artificial neural network simulation of hourly groundwater levels in a coastal aquifer system of the Venice lagoon. Engineering Applications of Artificial Intelligence, 25(8), 1670-1676. [doi:10.1016/ j.engappai.2012.02.009]
Turgeon, A. 1981. Optimal short-term hydro scheduling from the principle of progressive optimality. Water Resources Research, 17(3), 481-486. [doi:10.1029/WR017i003p00481]
Wu, C. L., Chau, K. W., and Li, Y. S. 2009. Predicting monthly streamflow using data-driven models coupled with data-preprocessing techniques. Water Resources Research, 45(8), 1-23. [doi:10.1029/ 2007WR006737]
Wu, R. S. 1988. Derivation of Balancing Curves for Multiple Reservoir Operation. M. E. Dissertation. NewYork: Cornell University.
Wurbs, R. A. 1993. Reservoir-system simulation and optimization models. Journal of Water Resources Planning and Management, 119(4), 455-472. [doi:10.1061/(ASCE)0733-9496(1993)119:4(455)]
Xiao, Y., Guo, S. L., Liu, P., Yan, B. W., and Chen, L. 2009. Design flood hydrograph based on multi-characteristic synthesis index method. Journal of Hydrologic Engineering, 14(12), 1359-1364. [doi:10.1061/(ASCE)1084-0699(2009)14:12(1359)]
Xie, W., Ji, C. M., Yang, Z. J., and Zhang, X. X. 2012. Short-term power generation scheduling rules for cascade hydropower stations based on hybrid algorithm. Water Science and Engineering, 5 (1), 46-58. [doi:10.3882/j.issn.1674-2370.2012.01.005]
Yeh, W. W. G. 1985. Reservoir management and operations models: A state-of-the-art review. Water Resources Research, 21(12), 1797-1818. [doi:10.1029/WR021i012p01797]
(Edited by Fang WANG)
This work was supported by the National Natural Science Foundation of China (Grant No. 51190094) and the National Key Technologies Research and Development Program of China (Grant No. 2009BAC56B02).
*Corresponding author (e-mail: slguo@whu.edu.cn )
Received Mar. 8, 2014; accepted Jun. 25, 2014
 Water Science and Engineering2014年4期
Water Science and Engineering2014年4期
- Water Science and Engineering的其它文章
- Water Science and Engineering ISSN 1674-2370, CN 32-1785/TV Vol. 3, Nos.1-4 2010 TOTAL CONTENTS
- Design formulas of transmission coefficients for permeable breakwaters
- Sea level change under IPCC-A2 scenario in Bohai, Yellow, and East China Seas
- Simulation-optimization model of reservoir operation based on target storage curves
- Comparison between dynamic programming and genetic algorithm for hydro unit economic load dispatch
- Purification and utilization of garlic processing wastewater in lotus pond wetlands
