Simulation-optimization model of reservoir operation based on target storage curves

Hong-bin FANG, Tie-song HU*, Xiang ZENG, Feng-yan WU

1. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, P. R. China

2. Hubei Water Resources Research Institute, Wuhan 430070, P. R. China

Simulation-optimization model of reservoir operation based on target storage curves

Hong-bin FANG1, Tie-song HU*1, Xiang ZENG1, Feng-yan WU2

1. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, P. R. China

2. Hubei Water Resources Research Institute, Wuhan 430070, P. R. China

This paper proposes a new storage allocation rule based on target storage curves. Joint operating rules are also proposed to solve the operation problems of a multi-reservoir system with joint demands and water transfer-supply projects. The joint operating rules include a water diversion rule to determine the amount of diverted water in a period, a hedging rule based on an aggregated reservoir to determine the total release from the system, and a storage allocation rule to specify the release from each reservoir. A simulation-optimization model was established to optimize the key points of the water diversion curves, the hedging rule curves, and the target storage curves using the improved particle swarm optimization (IPSO) algorithm. The multi-reservoir water supply system located in Liaoning Province, China, including a water transfer-supply project, was employed as a case study to verify the effectiveness of the proposed join operating rules and target storage curves. The results indicate that the proposed operating rules are suitable for the complex system. The storage allocation rule based on target storage curves shows an improved performance with regard to system storage distribution.

reservoir operation; joint operating rules; simulation-optimization model; improved particle swarm optimization

1 Introduction

Inter-basin water transfer-supply projects are mainly meant to rectify the imbalance between supply and demand in the water shortage region, so as to realize appropriate allocation of water resources. For a multi-reservoir water supply system with transfer-supply projects, joint operating rules should answer three basic questions: (1) the amount of water to be diverted in a period; (2) the total amount of water supplied to meet the joint demands; (3) and the amount of water to be released from each individual reservoir. The three questions are connected to one another, so they should be addressed at the same time.

Operation policy is essential for reservoir operation as the impact of the operation on the society and economy is significant (Sui et al. 2013). Some types of reservoir operating ruleshave been discussed in previous studies (Lund and Guzman 1999).

Previous research on the water diversion rule to determine the amount of water to be transferred has mainly been focused on systems of separated recipient reservoirs without joint demands (Xi et al. 2010; Sadegh et al. 2010; Li et al. 2009).

Hedging rule curves are often employed to trigger the hedging rule, and are often applied in operation of a single reservoir to determine the release to meet the demands (Tu et al. 2003). However, for the multi-reservoir system with joint demands in this study, the reservoir aggregation method is an effective approach for transforming a multi-reservoir system into an equivalent reservoir (aggregated reservoir) (Brandão 2010; Guo et al. 2011b). The reservoir aggregation method performs well in determining suitable total release from a water supply system.

For parallel multi-reservoir water supply systems having joint demands, that is, downstream demands that can be satisfied by any one or more of the multiple reservoirs, two rules are usually used to define the spatial distribution of reservoir storage volumes (Oliveira and Loucks 1997). The space rule attempts to equalize the ratio of available space in each of the parallel reservoirs at the end of a period to the expected inflow into each reservoir during the remainder of the refill season, while the New York City (NYC) rule attempts to equalize the probability of filling of each reservoir. Both the space and the NYC rules attempt to avoid a situation in which some reservoirs are spilling over while others remain unfilled (Lund and Guzman 1999), but they cannot be applied directly and do not provide clear indications on how to operate a complex system that has several purposes and heavy constraints. There is another frequently used method in actual application, referred to as the compensation regulation rule (Guo et al. 2011a), by which small-capacity reservoirs in systems supply water to meet the joint demand first and then the remaining water is supplied by large-capacity reservoirs. Although operation by this rule is simple, the results are sometimes imperfect.

Additionally, most researchers just focus on one or two questions. Study of multi-reservoir systems including water transfer-supply projects should concurrently consider the three issues listed above.

In this study, an improved storage allocation rule based on target storage curves (Perera and Codner 1996; Lund and Ferreira 1996) is proposed. Join operating rules are also proposed based on a water diversion rule, a hedging rule based on an aggregated reservoir, and a storage allocation rule. A simulation-optimization model was established for a multi-reservoir system, including a water transfer-supply project, located in northern China. The improved particle swarm optimization (IPSO) algorithm (Jiang et al. 2007) in combination with the simulation model were employed to optimize the decision variables, including the key points of water diversion curves, hedging curves, and target storage curves. Different schemes, including other operating rules, were also implemented to simulate the operation of the system for verifying the reasonability and applicability of the proposed rules.

2 Joint operating rules

The joint operating rules include a water diversion rule to determine the amount of diverted water, a hedging rule based on an aggregated reservoir to determine the total release from the system to meet joint demands, and a storage allocation rule to determine the release from each reservoir. The water diversion rule should be employed first. The hedging rule curve can help in making reasonable decisions at the same time. After that, the system storage in the multi-reservoir system can be determined and the target storage curve can specify the amount of water to be released from each individual reservoir.

2.1 Water diversion rule

In this study, p is used to denote the number of time periods within a year. Two threshold vectors, X=(x1,x2,… ,xp)Tand Y=(y1,y2,… ,yp)T, were set, which constitute water diversion operating curves. X constitutes the curve for reservoirs without need of water diversion, and Y constitutes the curve for reservoirs with the need of maximum amount of diverted water. xtand ytare water storage thresholds in time period t, with the value less than the storage capacity, and xt≥ytshould be satisfied for any period t(t = 1,2,… ,p). As shown in Fig. 1, X and Y divide the water space of the reservoir into three areas, including an area without water diversion, an area with decreasing diverted water, and an area with maximum diverted water. The amount of diverted water in each period can be estimated by

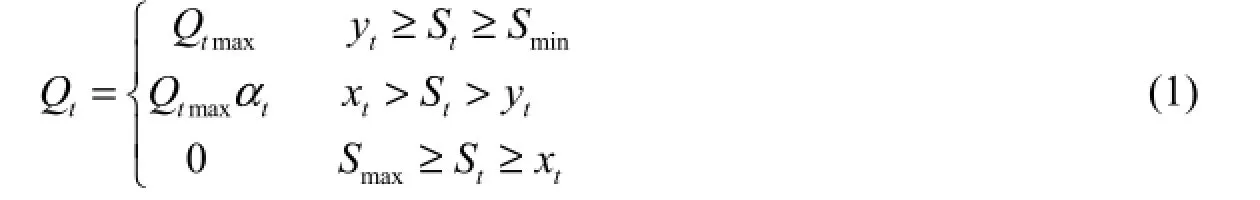
where Qtand Qtmaxare the amount of diverted water and maximum allowable amount of diverted water in time period t, respectively; Smaxand Sminare the maximum and minimum storage capacity of the recipient reservoir, respectively; Stis the initial water storage in time period t; and αtis a rationing factor for water diversion in time period t, with 0 ＜ αt＜ 1.

Fig. 1 Sketch of water diversion operating curves

2.2 Hedging rule based on aggregated reservoir

For joint water demands that can be satisfied by any individual reservoir, reservoiraggregation is implemented for the hedging rule (Brandão 2010). Hedging rules for reservoir operations can be presented in different ways. The hedging rule adopted in this study used the beginning-of-period storage of an aggregated reservoir, which is one hypothetical reservoir replacing the reservoir system, as a trigger to start hedging. The total release from the multi-reservoir system to meet water demand in each period is specified based on the planned water supply (or water demand) and the relationship between the hedging rule curves and the existing water storage in the system.

The proposed hedging rule based on the aggregated reservoir consists of hedging rule curves and rationing factors for each water demand type. For single-purpose water-supply reservoir operation, the water demand can be divided into various categories, such as agricultural, industrial, and domestic water demand. It should be noted that different kinds of water demand require different reliabilities and different degrees of hedging in practice. Di,t(i = 1,2,3) is used here to denote different kinds of water demand in time period t, arranged in the order of priority, from highest to lowest. Corresponding threshold vectors Zi=(zi,1,zi,2,…,zi,p)Twere set, where z1,t≤ z2,t≤ z3,texisted in all time periods, and z1,t, z2,t, and z3,tare the water storage thresholds of the aggregated reservoir corresponding to D1,t, D2,tand D3,tin time period t, respectively. As shown in Fig. 2, Zidivides water space of the aggregated reservoir into four areas, where Vmaxand Vmindenote the maximum and minimu m storage capacity of the aggregated reservoir, respectively. The hedging rule in different areas for determining the total amount of water supply to meet joint demands is expressed as

where Jtis the total amount of water supply meeting joint demands in time period t, Vtis the initial water storage in the aggregated reservoir in time period t, and βi(i = 1, 2, 3)is the rationing factor for hedging corresponding to Di,t(i = 1,2,3), respectively. The value of rationing factors can be obtained either by optimization or according to the experts’ knowledge.

Fig. 2 Sketch of hedging rule based on aggregated reservoir

2.3 Allocation rule based on target storage curves

Target storage curves define the spatial distribution of reservoir storage volumes within a multiple reservoir system, using the fitting or optimization method (Lund and Ferreira 1996; Oliveira and Loucks 1997). Fig. 3 illustrates the target storage curves for a two-reservoir system. For a given system storage V at a given period, the curves specify the storage volumes of reservoirs 1 and 2 as, respectively, and. Thus, the gradient of the total storage line equals 1. If the gradient of the target storage curves of the two reservoirs is less than that of the total storage line, then the excess water should be stored in both reservoirs. The amount of water stored is related to the gradient of the target storage curves. After the total system storage reaches point H in Fig. 3, the gradient of the target storage curve of reservoir 1 changes to 0 because reservoir 1 has reached full capacity. Then, the change of the total storage is equal to that of the storage of reservoir 2.

Fig. 3 Sketch of target storage curves

In this study, the target storage curves for reservoirs in each period were defined by connected piecewise linear functions with end points A, B, C, and D for reservoir 2 and A, E, F, and G for reservoir 1, as shown in Fig. 3. For a multiple reservoir system, according to the net total system storage determined by the water supply rule at the end of period t, the target storageof reservoir i can be computed. The remaining storage Si′,tfor reservoir i in time period t can be express as:

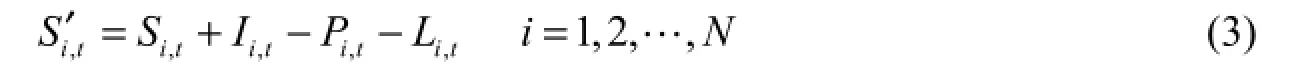
where Si,tis the initial storage of reservoir i in time period t, Ii,tand Li,tdenote the inflow and loss in reservoir i in time period t, respectively, Pi,tis the amount of water supply of reservoir i for individual demand in time period t, and N is the number of reservoirs. By comparing the remaining storage and the target storage, the storage allocation rule for joint demands can be defined as follo ws:

3 Simulation-optimization model

3.1 Objective function and constraints

The main purpose of water transfer is to alleviate water shortages in recipient regions. At the same time, water spills related to the redundant diverted water should be avoided. Then, the objective function is as follows:

Subject to

where Hj,tis the water shortage at demand node j in time period t, Ejis the shortage index at demand node j, Dj,tand Rj,tdenote the water demand and the amount of water supply at demand node j in time period t , respectively, ω1and ω2are the weighting factors, G is the total number of demand nodes, and T is the total number of time periods. The following constraints are applied to the model:

(1) Water balance equations:

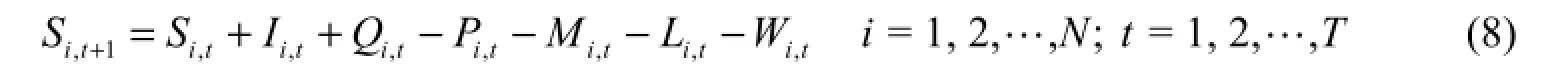
(2) Water storage capacity constraints:

(3) Conveyance capacity constraints of the water diversion:

(4) Relationship between the total amount of water supply for joint demands and that from an individual reservoir:

(5) Release constraints:

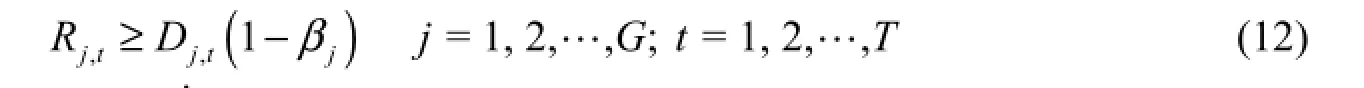
(6) Target storage constraints:

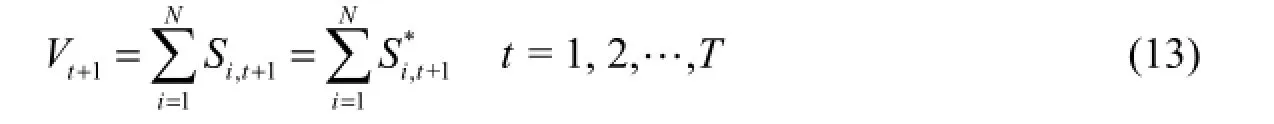
(7) System spill constraints:

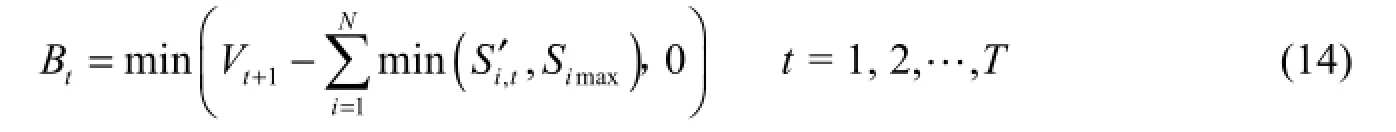
where Wi,tand Btare the spills of reservoir i and the system in time period t, respectively, Siminand Simaxarethe minimum and maximum allowable water storage for reservoir i, respectively, and Mi,tis the amount of water supply of reservoir i for joint demand in time period t.

3.2 Method solution

In this study, the simulation-optimization model included system simulation model and optimization model using the heuristic algorithm. The general framework of the model is shown in Fig. 4.

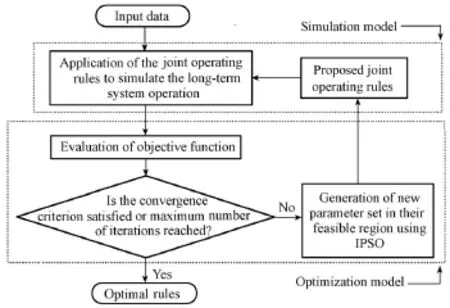
Fig. 4 Framework of simulation-optimization of joint operation

The simulation model was used to recreate the long-term operation of the muti-reservoir system with the rule curves (Chau et al. 2005; Chen and Chaw 2006; Zeng et al. 2014). The decision variables in the optimization model include water diversion curves, water supply curves based on the aggregated reservoir, and target storage curves, with the threshold vectorsin Fig.1,thethreshold vectorsin Fig.2, andthecoordinates of pointsA, B,C,D, E,F,andG in Fig. 3. The procedures to simulate the operation were as follows:

Step 1: According to the water diversion rule, the amount of diverted water was definedas a function of the current storage of the recipient reservoir and maximum amount of diverted water, as described by Eq. (1).

Step 2: The hedging rule based on an aggregated reservoir was used to determine the total water release needed to meet joint water demands during the water diversion operation, as described by Eq. (2).

Step 3: Finally, the target storage of each reservoir was defined as a function of system storage at the end of the period and the target storage curves. Then, the allocation rule was used to determine the amount of water released from each reservoir.

At the end of the current period, the simulation procedure moved to step 1, and the water balance terms for the next period were calculated. The simulation model proceeded in iterations until the end of the long-term operation, then provided the statistic indices related to the decision variables for the optimization model. Then, heuristic strategies were adopted to look for the combination of parameters that provide the best reservoir operating performance.

Due to nonlinearity, discontinuity, and discreteness of modern simulation models used in solving complex problems, heuristic search procedures are developed rapidly nowadays (Cheng et al. 2012; Xie et al. 2012; Chen and Chau 2006). The particle swarm optimization (PSO) algorithm was proposed by Kennedy and Eberhart (1995). As a population-based search algorithm, PSO uses local and global search capabilities to find better quality solutions based on simulation of the social behavior of a flock of birds. However, PSO also shows premature convergence, especially in complex multi-peak search problems (Jiang et al. 2007; Zeng et al. 2014). By integrating competitive evolution, decomposition, and complex shuffling into the standard PSO algorithm, an improved particle swarm optimization (IPSO) algorithm was proposed. The algorithm has greater breadth and depth when searching than the standard PSO algorithm (Jiang et al. 2007). In recent years, the IPSO algorithm has been widely applied to reservoir system operation (Zhang et al. 2011; Zeng et al. 2014).

In this study, the IPSO algorithm (Jiang et al. 2007) was used to solve optimization problems. The procedures we followed are described below:

Step 1: Initial L×P particles within the feasible region were generated randomly, where L is the number of population and P is the number of particles in each population.

Step 2: The population was sorted into one primary group and L−1 subordinate groups.

Step 3: The particles in each subordinate group were evolved using the standard PSO.

Step 4: The velocity and position of each particle in the primary group were updated according to the information in the primary group and the subordinate groups.

Step 5: All particles were mixed and their information was exchanged after a certain number of iterations.

Step 6: If the maximum number of iterations was reached, the procedure was stopped. Otherwise, the procedure returned to step 2.

More detailed steps about the algorithm are provided in Jiang et al. (2007).

4 Case study

4.1 Biliuhe and Yingnahe reservoirs

Both the Biliuhe and Yingnahe reservoirs are located in Liaoning Province, China, where the flood season is from July to September. The active storages of the Biliuhe and Yingnahe reservoirs are 644 × 106m3and 217 × 106m3, respectively, while that of the Biliuhe Reservoir decreases to 594 × 106m3for flood control during the flood season. The system of Biliuhe-Yingnahe reservoirs functioning in parallel should supply water to meet joint demands for industry and agriculture,while both reservoirs are subject to individual demands for environmental purposes. Simultaneously, the Biliuhe Reservoir can receive diverted water through the water transfer-supply project. According to the requirements of design, the water diversion capacity over a year is about 300 × 106m3.

4.2 Results and discussion

The rationing factor for water diversion has been empirically determined to be 0.5, and the rationing factors for the agricultural and industrial water supply are 0.7 and 0.9, respectively. The weighting factors ω1and ω2in Eq. (5) were finally chosen to be 80 and 1, respectively, based on the results of trial and error calculation. In the IPSO method, the weight coefficient decreases from 0.9 to 0.4 linearly with the increase of the sub-swarm iteration times. The weighting factors equal 2.0 in the standard PSO method. The number of sub-swarms was 4, and there were 150 particles in each sub-swarm. The maximum number of iterations was 2 000.

In order to analyze the effectiveness of the proposed rules, different operating rules were employed for comparison. Five schemes listed in Table 1 were set up. According to the full diversion rule, the water diversion capacity has a uniform distribution over each time period within a year.

Table 1 Description of different schemes

Inflow data for the system were a series of hydrological records of 53 years from 1951 to 2003. According to the distribution of runoff, the hydrological year was divided into four operating periods: before the flood season (May to June), the flood season (July to September), after the flood season (October to November), and the drought season (December to April). Thus, each of the decision variables for operating curves contained four variables. Water diversion loss was about 4%. Results of different schemes are shown in Table 2, from which some conclusions can be drawn.

Table 2 Results of different schemes

(1) Scheme 1 obtains the optimal index of water shortage and water supply as compared with other schemes, which demonstrates the superiority of the proposed rules.

(2) The annual average amount of water diversion in scheme 1 is 0.04 × 109m3less than that in scheme 2, and the shortage index also decreases,which demonstrates that the proposed water diversion rule is more reasonable than the full diversion rule.

(3) The shortage index of scheme 1 is smaller than that of scheme 4, and the shortage index of scheme 3 is smaller than that of scheme 5, which indicates that the storage allocation rule based on target storage curves is more effective than the compensation regulation rule, whether water diversion exists or not.

The annual water diversion and spill processes for different years are shown in Fig. 5, based on the results of simulation. Water spills do not occur when the annual amount of water diversion reaches its maximum, such as in the years 2000 to 2003. The results also indicate that the trend of water diversion is contrary to that of spilling. This shows that the optimization of the water diversion process is reasonable and effective.

Fig. 5 Annual water diversion and spill processes for different years

In parallel multi-reservoir water supply systems, excellent operating rules should be able to equalize probability of spilling among reservoirs in the refill season (Lund and Guzman 1999) and that of empty reservoirs existing in the drawdown season (Wu 1988), which indicates that there is a significant positive correlation between reservoirs’ storage rates (the ratio of the reservoir’s storage to its capacity). Distribution of storage rates under different allocation rules are shown in Fig. 6. x and y denote the average storage rates of Biliuhe and Yingnahe reservoirs, respectively, and r2is the correlation coefficient of x and y. A highercoefficient r2indicates a more reasonable allocation of system storage. Fig. 8 shows that the correlation coefficient r2of scheme 1 is almost twice as large as that of scheme 4, which demonstrates that the allocation rule based on the target storage curves are more effective than the compensation regulation rule in system storage allocation.

As shown in Fig. 6, the storage rate of the Yingnahe Reservoir is mostly less than 0.1 and the average rate of the Biliuhe Reservoir is 0.82 for scheme 4. The reason is that water is always released from the Yingnahe Reservoir and diverted into the Biliuhe Reservoir, which results in a large amount of spilling from Biliuhe Reservoir (as described in Table 2).

Fig. 6 Distribution of storage rates under different schemes

Fig. 7 shows the distribution of system storage using the compensation regulation rule. Using the fitting method, the target storage curves corresponding to the compensation regulation rule are obtained as shown in Fig. 7. This implies that the allocation rule based on this special target storage curve can obtain the same result as the compensation regulation rule. Thus, the compensation regulation rule is a special case of the storage allocation rule based on target storage curves. The target storage curve of the storage allocation rule proposed in this study is obtained using the optimization algorithm, and is more reasonable than that of the compensation regulation rule.

Fig. 7 Storage distribution of compensation regulation rule

5 Conclusions

This paper proposes a set of new joint operating rules including a water diversion rule, a hedging rule based on an aggregated reservoir, and a storage allocation rule based on target storage curves. Based on the results from the simulation-optimization model established for a multi-reservoir system in Northern China, the following conclusions can be drawn. First, the proposed joint operating rules can lead to a preferable performance in comparison to other rules. Second, the storage allocation rule based on target storage curves is more effective than the compensation regulation rule. It can also lead to a higher correlation coefficient between the storage rates of different reservoirs in a parallel multi-reservoir system. The joint operating rules provide an effective method for operation of water supply systems with complex hydraulic characteristics.

However there are some limitations in actual application. First, as the number of reservoirs increases, the efficiency of joint operating rules and optimization algorithms needs to be further examined. Second, one of the important assumptions in this study was that inflows of reservoirs in the current time period were known. Therefore, the proposed rules should be used in combination with a suitable runoff forecasting model in actual application.

The following topics are suggested for further investigation of joint operating rules. This study integrated decision variables in several adjacent periods in all three operating rules. The sensitivities of these periods should be considered in detail before integration. In addition, further investigation of hydropower systems of reservoirs in series using an allocation rule based on target storage curves would be of value.

Brandão, J. L. B. 2010. Performance of the equivalent reservoir modelling technique for multi-reservoir hydropower systems. Water Resources Management, 24(12), 3101-3114. [doi:10.1007/s11269 -010-9597-9]

Chau, K. W., Wu, C. L., and Li, Y. S. 2005. Comparison of several flood forecasting models in Yangtze River. Journal of Hydrologic Engineering, 10(6), 485-491. [doi:10.1061/(ASCE)1084-0699(2005)10:6(485)]

Chen, W., and Chau, K. W. 2006. Intelligent manipulation and calibration of parameters for hydrological models. International Journal of Environment and Pollution, 28(3-4), 432-447. [doi:10.1504/ IJEP.2006.011221]

Cheng, C. T., Shen, J. J., Wu, X. Y., and Chau, K. W. 2012. Short-term hydroscheduling with discrepant objectives using multi-step progressive optimality algorithm. JAWRA Journal of the American Water Resources Association, 48(3), 464-479. [doi:10.1111/j.1752-1688.2011.00628.x]

Guo, X. N., Hu, T. S., Zeng, X., and Li, X. J. 2011a. Two-dimensional scheduling chart for jointly water-supply operation of dual-reservoir systems. Journal of Huazhong University of Science and Technology (Nature Science Edition), 39(10), 121-124. (in Chinese).

Guo, X. N., Hu, T. S., Huang, B., and Han, Y. C. 2011b. Joint operation rules for multi-reservoir water supply system based on the model of simulation and optimization. Journal of Hydraulic Engineering, 42(6), 705-712. (in Chinese).

Jiang, Y., Hu, T. S., Huang, C. C., and Wu, X. N. 2007. An improved particle swarm optimization algorithm. Applied Mathematics and Computation, 193(1), 231-239. [doi:10.1016/j.amc.2007.03.047]

Kennedy, J., and Eberhart, R. 1995. Particle swarm optimization. Proceedings of the IEEE InternationalConference on Neural Networks, 1942-1948. Washington, D.C.: IEEE Press. [doi:10.1109/ ICNN.1995.488968]

Li, X. S., Wang, B. D., Mehrotra, R, Sharma, A, and Wang, G. L. 2009. Consideration of trends in evaluating inter-basin water transfer alternatives within a fuzzy decision making framework. Water Resources Management, 23(15), 3207-3220. [doi:10.1007/s11269-009-9430-5]

Lund, J. R., and Ferreira, I. 1996. Operating rule optimization for Missouri River reservoir system. Journal of Water Resources Planning and Management, 122(4), 287-295. [doi:10.1061/(ASCE)0733-9496 (1996)122: 4(287)]

Lund, J. R., and Guzman, J. 1999. Derived operating rules for reservoirs in series or in parallel. Journal of Water Resources Planning and Management, 125(3), 143-153. [doi:10.1061/(ASCE)0733-9496 (1999)125:(143)]

Oliveira, R., and Loucks, D. P. 1997. Operating rules for multireservoir systems. Water Resources Research, 33(4), 839-852. [doi:10.1029/96WR03745]

Perera, B. J. C., and Codner, G. P. 1996. Reservoir targets for urban water supply systems. Journal of Water Resources Planning and Management, 122(4), 270-279. [doi:10.1061/(ASCE)0733 -9496(1996)122:4(270)]

Sadegh, M., Mahjouri, N., and Kerachian, R. 2010. Optimal inter-basin water allocation using crisp and fuzzy Shapley games. Water Resources Management, 24(10), 2291-2310. [doi:10.1007/s11269-009-9552-9]

Sui, X., Wu, S. N., Liao, W. G., Jin, T. T., and Zhang, X. 2013. Optimized operation of cascade reservoirs on Wujiang River during 2009-2010 drought in southwest China. Water Science and Engineering, 6(3), 308-316. [doi:10.3882/j.issn.1674-2370. 2013.03.007]

Tu, M. Y., Hsu, N. S., and Yeh, W. W. G. 2003. Optimization of reservoir management and operation with hedging rules. Journal of Water Resources Planning and Management, 129(2), 86-97. [doi:10.1061/ (ASCE)0733-9496(2003)129:2(86)]

Wu, R. S. 1988. Derivation of Balancing Curves for Multiple Reservoir Operation. M. E. Dissertation. New York: Cornell University.

Xie, W., Ji, C. M., Yang, Z. J., and Zhang, X. X. 2012. Short-term power generation scheduling rules for cascade hydropower stations based on hybrid algorithm. Water Science and Engineering, 5(1), 46-58. [doi:10.3882/j.issn.1674-2370. 2012.01.005]

Xi, S. F., Wang, B. D., Liang, G. H., Li, X. S., and Lou, L. L. 2010. Inter-basin water transfer-supply model and risk analysis with consideration of rainfall forecast information. Science China Technological Sciences, 53(12), 3316-3323. [doi:10.1007/s11431-010-4170-6]

Zeng, X., Hu, T. S., Guo, X. N., and Li, X. J. 2014. Water transfer triggering mechanism for multi-reservoir operation in inter-basin water transfer-supply project. Water Resources Management, 28(5), 1293-1308. [doi:10.1007/s11269-014-0541-2]

Zhang, J., Wu, Z., Cheng, C. T., and Zhang, S. Q. 2011. Improved particle swarm optimization algorithm for multi-reservoir system operation. Water Science and Engineering, 4(1), 61-73. [doi:10.3882/j.issn.1674-2370.2011. 01.006]

(Edited by Yan LEI)

This work was supported by the National Natural Science Foundation of China (Grants No. 51339004 and 71171151).

*Corresponding author (e-mail: tshu@whu.edu.cn)

Received Jan. 13, 2014; accepted Aug. 5, 2014