电力变压器主绝缘电场的数值分析

刘凤英，韩 磊，张喜乐，，张 萍，王浩名，张宇萌

（1.保定天威集团有限公司，河北 保定 071056；2.河北工业大学 电气工程学院，天津 300130）

电力变压器主绝缘电场的数值分析

刘凤英1，韩 磊2，张喜乐1，2，张 萍2，王浩名1，张宇萌2

（1.保定天威集团有限公司，河北 保定 071056；2.河北工业大学 电气工程学院，天津 300130）

在分析电力变压器结构特点的基础上，对典型产品建立了主绝缘电场计算模型，利用有限元计算软件进行了数值计算，并对影响绕组端部电场的因素进行了分析，由此得到了主绝缘电场的分布、最大电场强度及其发生部位.通过对两类软件计算结果的比较及产品的各项绝缘试验，相互检验了计算方法与软件结果的合理性，为电力变压器的绝缘设计提供了有效的分析方法.

电力变压器；主绝缘；电场；数值分析

变压器是电力系统的重要设备，无论是发电厂、变电所、输配电网络还是广大用户，都使用着各种各样的变压器.随着国民经济的不断发展，对电力的需求越来越大，电力变压器随之趋于高电压、大容量方向发展.然而，要提高变压器的容量和电压等级，必须首先解决变压器的绝缘问题.电力设备运行故障统计表明，绝缘结构的损坏是导致变压器故障的主要原因之一，因此，提高变压器的运行可靠性和进行合理的绝缘设计，就成为变压器设计极其重要的部分[1].目前，在电力变压器绝缘结构设计中采用2种计算方法[2-3]：一种是经验解析公式，该方法简单、快捷，其缺点是难以满足复杂绝缘结构及高可靠性的技术要求；另一种方法就是数值计算方法，该方法可以提供直观、较准确的电场分布和场量结果，但容易受到构建模型及材料属性等因素的影响，因此，该方法的工程有效性仍然需要在产品实际应用中检验与完善.本文就是通过对一台典型电力变压器主绝缘电场进行模型构建及数值分析，并利用同类软件计算结果的比较及产品绝缘试验，相互检验计算方法与软件的合理性，为电力变压器的绝缘结构设计提供有效的分析方法.

1 对通用软件计算结果的测试

同心圆柱电容器结构如图1所示.

具有单一均匀介质的同心圆柱电容器间的电场强度为：

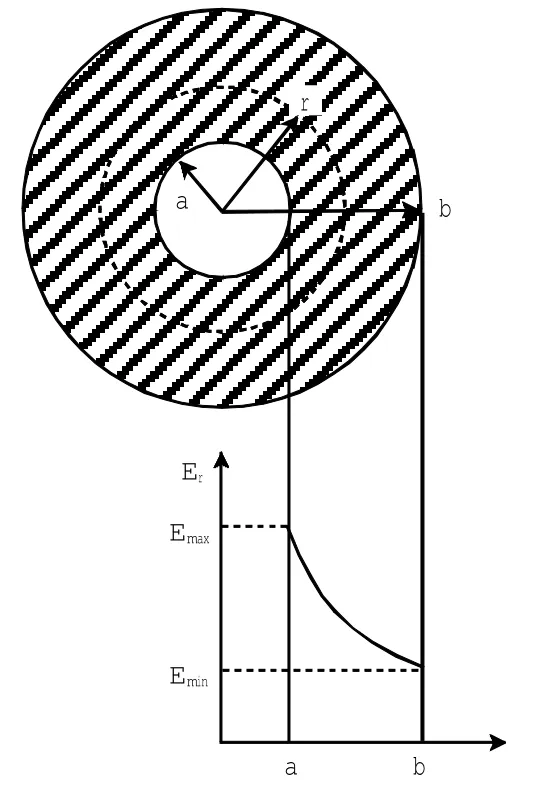
图1 同心圆柱电容器Fig.1 Cylindrical capacitor

式中：U为电极间电压（kV）；a、b分别为内、外电极的半径（mm）.

现设同心圆柱电容器的长度L为1 000 mm，内径a为50 mm，外径b为150 mm，其间充满介电常数为ε的介质，内、外导体间的电压U为10 kV.因为电容器的长度远大于截面半径，可忽略边缘效应，故可由公式（1）求得Er.

利用软件ElecNet建立与上述条件对应的轴对称场计算模型，其仿真结果如图2所示.

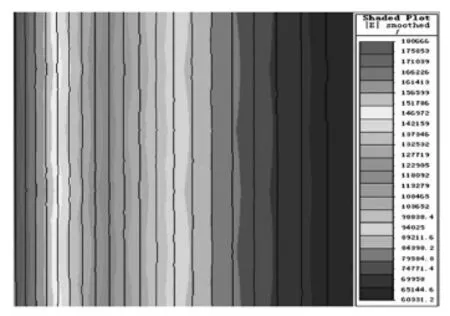
图2 电场强度分布云图Fig.2 Distribution of EF stress

图3所示为在不同r时解析法与数值法电场强度的比较.从图3中不难发现，这2种方法所得结果几乎相吻合，而且相对误差在0.05%～1.04%之间.由此可知，通用电场软件ElecNet的计算结果合理、可靠.

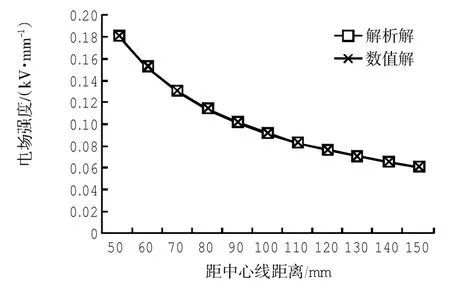
图3 在不同r时解析法与数值法的电场强度比较Fig.3 EF stress obtained by formulated and numerical method with radius r variation

2 典型变压器主绝缘电场的数值分析

2.1 数学物理模型

本文所分析的电力变压器为220 kV端部绝缘结构.其模型主要由低压绕组、调压绕组、中压绕组、高压绕组、绝缘纸筒、变压器油、角环和静电环等组成.为简化分析，计算时做如下假定[4-6]：①按线性、稳态轴对称电场计算；②变压器油、绝缘纸和绝缘纸筒介电常数分别取为2.2、3.5、4.4；③忽略引线对端部电场的影响.根据上述简化，所选电力变压器绝缘结构模型如图4所示.图4中模型的左边界和上边界是铁心和铁轭，为地电位和一类齐次边界条件；绕组与静电环为已知的高电位.右边界和下边界为二类齐次边界条件.

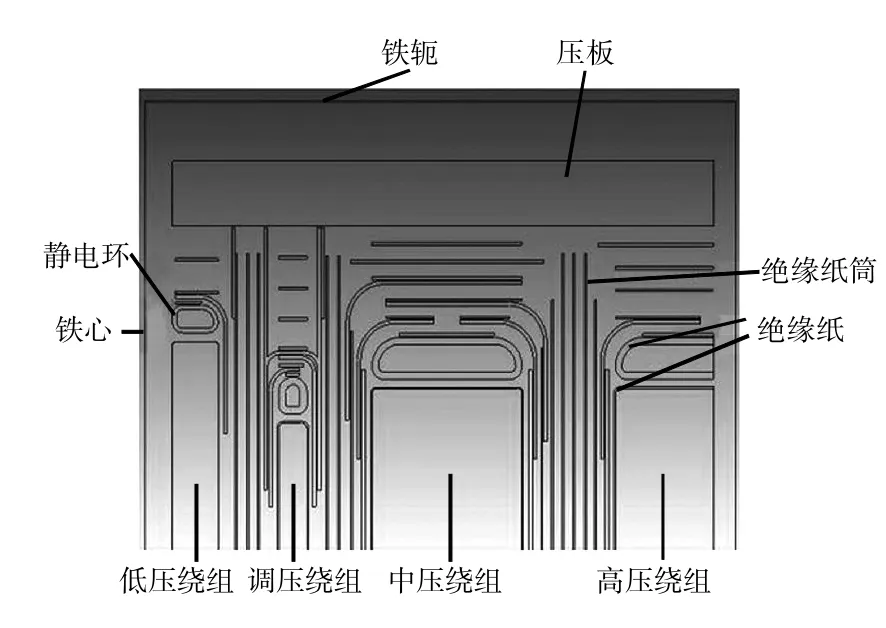
图4 主绝缘电场简化模型Fig.4 Simplified model of main insulation EF

在实际的建模过程中，由于模型较复杂，可用AutoCAD进行建模，然后将此模型导入ElecNet中.对于轴对称场，必须使导入模型的铁心轴线与ElecNet软件默认的旋转轴（y轴）相重合，然后将导入模型进行旋转拉伸、赋材料属性、为绕组和静电环施加电压、确定边界条件，并进行仿真.

对应的电场边值问题为：

式中：S1为强加一类边界，包括已知地电位和高电位；S2为二类齐次边界；k为材料的介电常数.

2.2 计算结果与分析

利用通用电场仿真软件ElecNet和构建的轴对称电场计算模型，计算了电力变压器在交流工频情况下的主绝缘电场分布，得到了最大电场强度及其发生部位.

通过计算所得到的变压器主绝缘电场及等位线分布如图5所示.

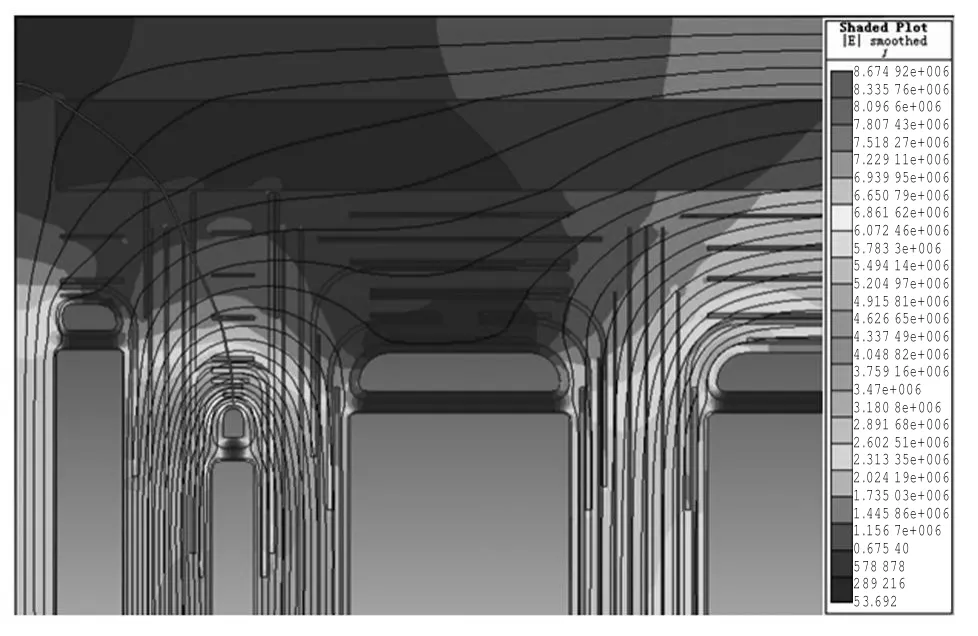
图5 主绝缘电场及等位线分布Fig.5 Distribution of main insulation EF and potential line

由图5可知，电场较集中的部位发生在调压绕组静电环的拐角附近及调压绕组到低压绕组这一区域；低压绕组与铁心、各绕组间的电场近似为均匀电场；各绕组端部之间和高压绕组到铁轭间电场为非均匀电场.最大电场强度为8.675 kV/mm，发生于调压绕组静电环上表面的临近油隙中，图5给出了过此部位的电力线，图6为沿所示电力线的电场强度分布.

2.3 影响因素分析

为了分析绝缘角环和静电环对主绝缘电场分布的影响，在已有模型的基础上，保持其他部分不变，针对高压绕组部分，分别考察其无角环与静电环、无角环但有静电环以及同时放置角环和静电环的3种情况，从而，确定角环及静电环对电场强度分布的影响变化规律.

2.3.1 无角环与静电环的电场分析

高压绕组端部无角环与静电环时的电场分布如图7所示，此部分最大场强发生在高压绕组左上拐角的油纸交界面处，为5.976 kV/mm，相应的绝缘裕度为1.16.

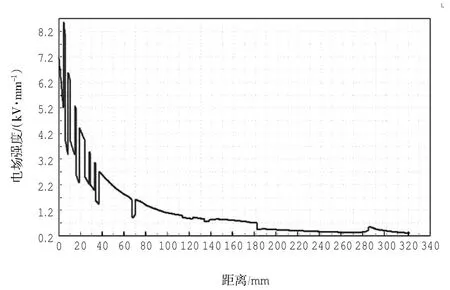
图6 沿电力线的电场强度分布图Fig.6 Distribution of EF stress along electric flux line

2.3.2 无角环和有静电环的电场分析

高压绕组端部无角环和有静电环时的电场分布如图8所示，此部分最大场强发生在高压绕组静电环左上角油纸交界面处，最大电场强度约为3.920 kV/ mm，对应的绝缘裕度为1.23.高压绕组的油纸交界面处电场强度为3.881 kV/mm，其绝缘裕度为1.73.加入静电环后，电场强度有了明显下降，最大电场强度由高压绕组油纸交界面处移到静电环的油纸交界面处，且绝缘裕度显著提高.

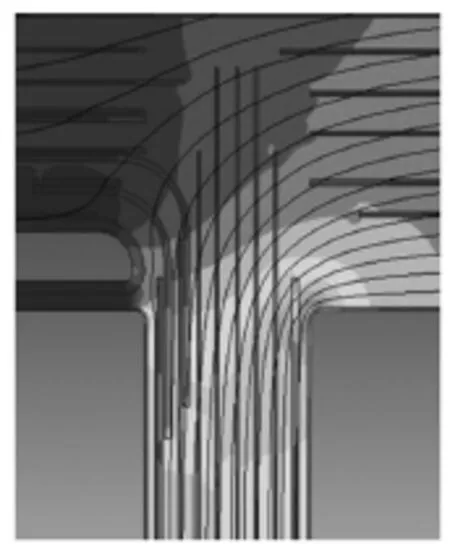
图7 无角环与静电环Fig.7 Without angle ring and electrostatic ring

图8 无角环和有静电环Fig.8 With electrostatic ring and without angle ring

2.3.3 同时放置角环和静电环的电场分析

高压绕组端部同时放置角环和静电环时的电场分布如图9所示，静电环左上角油纸交界面处的最大电场强度约为3.948 kV/mm，对应的绝缘裕度为1.62.可见加入角环后，虽然电场强度有所增加，但由于角环分隔油隙的作用，对应的许用场强和绝缘裕度却明显提高.

通过以上对高压绕组端部3种不同绝缘结构的电场分析，可得到如下结论：

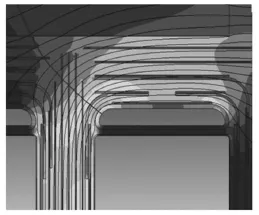
图9 放置角环和静电环Fig.9 With angle ring and electrostatic ring

（1）对无角环与静电板的电场分析可知，电场强度明显大于其他2种结构，且绝缘裕度偏小；

（2）对高压绕组端部放置静电环的电场分析可知，不仅降低了最大电场强度，使绝缘裕度提高，而且还改善了端部电场的分布；

（3）高压绕组端部放置角环，虽使端部的场强值有所增加，但其分割了端部油隙，显著提高了端部油隙的许用场强，增强了绝缘性能.

3 同类软件计算结果及对比分析

3.1 同类软件的计算结果

为了进一步确认和校算所分析产品结果的可靠性，利用变压器整体绝缘结构设计及电场分析专用软件（简称：EF2D）[7-8]，对同一台产品轴对称电场计算模型（图4）进行了数值计算.通过计算所得到的电场分布如图10所示.

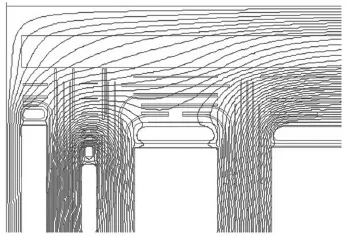
图10 主绝缘电场分布图Fig.10 Distribution of main insulation EF

从图10中可知，电场较集中的部位发生在调压绕组静电环的拐角附近及调压绕组到低压绕组这一区域，其最大场强为9.024 kV/mm.表1给出了各条电力线的最大平均电场强度（利用单元电场强度求得的电力线沿各段油隙上的最大平均场强值）、对应的许用电场强度和最小绝缘裕度的大小.由此可知，各条电力线的绝缘裕度均大于1，满足绝缘强度的要求.

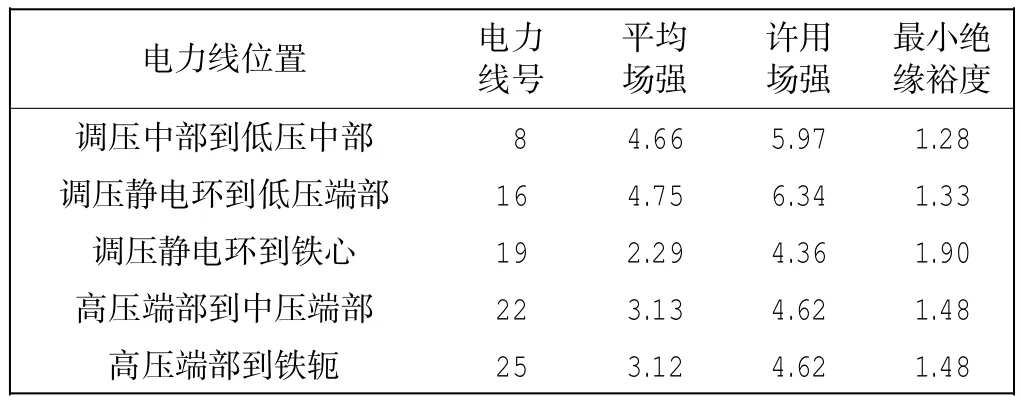
表1 典型位置各条电力线的场强及绝缘裕度Tab.1 EF stress and insulation margin of electric flux lines kV/mm

此外，由于不同部位电场强度的许用值随油隙尺寸的增加而按指数规律衰减变化，因此，最小绝缘裕度与最大电场强度不具有直接对应关系，如图11、图12分别为发生最小绝缘裕度的电力线（序号为8）和发生最大电场强度的电力线（序号为16）所在位置示意.

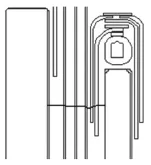
图11 最小绝缘裕度的电力线Fig.11 Electric flux line with minimum margin

3.2 软件之间的相互校验与分析

利用专用软件得到的最大场强为9.024 kV/mm，位于调压绕组静电环的上表面油隙，而利用通用软件所得到的最大电场强度为8.675 kV/mm，也位于调压绕组静电环上表面油隙，且相对误差仅为3.86%.比较图5和图10，可知电位的分布趋向一致，电场较密集的部位均发生在调压绕组静电环的拐角附近及调压绕组到低压绕组这一区域.由图5和图12可知，发生最大电场强度均为调压绕组静电环到铁心的这条电力线.两种软件在各绕组和静电环绝缘中的最大电场强度大小及位置比较结果如表2所示.

表2 电场强度的比较Tab.2 Comparison of EF stress kV/mm

由此可知，2种软件最大电场强度计算结果的相对误差在5.0%内.由专用软件得出电力线最小绝缘裕度为1.28，位于调压绕组中部与低压绕组中部之间，而由通用软件得到此位置的绝缘裕度为1.23，因此，通过对两类软件计算结果的比较，相互校验了计算软件与方法的有效性，使该台产品顺利通过了绝缘性能试验.

4 结论

对一台典型电力变压器端部绝缘结构建立了合理的计算模型，并进行了主绝缘电场的数值计算及影响因素分析，由此得到了如下应用结论：

（1）最大电场强度发生在调压绕组静电环的上表面油隙，其大小为8.675 kV/mm；

（2）两类软件电场分布趋于一致，最大电场强度的计算误差在5%内，绝缘裕度的计算误差在3%内，由此，相互检验了计算方法与软件的有效性；

（3）通过在绕组端部放置静电环和角环，不仅可改善端部电场的分布和降低最大电场强度，而且，由于分割了端部油隙，可显著提高油隙许用电场强度和绝缘可靠性.

通过该产品的各项绝缘试验，进一步验证了计算方法与应用结论的正确性.

[1] 谢毓城.电力变压器手册[M].北京：机械工业出版社，2005.

[2] 颜威利，杨庆新，汪友华，等.电气工程电磁场数值分析[M].北京：机械工业出版社，2006.

[3] 张喜乐，王建民，吴增泊，等.超高压直流换流变压器阀侧引出线电场的数值分析[J].变压器，2009，46(7)：1-5.

[4] 罗青林.关于800 kV换流变压器主绝缘研究 [J].变压器，2009，46（11）：7-9.

[5]EBISAWA Y，YAMADA S，MORI S，et al.DC creepage breakdown characteristics of oil-immersed Insulation[J].IEEE Trans on Dielectrics and Electrical Insulation，2009，16（6）：1686-1692.

[6]SCHULTZ K.Creepage withstand strength of transformer board[C]//WICON Insulation Conference.Rapperswil：Switzerland，1996.

[7]HASEGAWA T，YAMAJI K.Dielectric strength of transformer insulation at DC polarity reversal[J].IEEE Transactions on Power Delivery，1997，12（7）：1526-1531.

[8] 王建民，张喜乐，张国强，等.大型变压器主绝缘电场的全域分析工程仿真软件开发[J].变压器，2010，47（9）：15-18.

Numerical analysis of main insulation electric field for power transformer

LIU Feng-ying1，HAN Lei2，ZHANG Xi-le1，2，ZHANG Ping2，WANG Hao-ming1，ZHANG Yu-meng2
（1.Baoding Tianwei Group Co Ltd，Baoding 071056，China；2.College of Electronic Engineering，Hebei University of Technology，Tianjin 300130,China）

On the basis of analyzing the characteristics and the structure for a power transformer,the calculation model of main insulation electric field（EF）is established.Then,the numerical calculation and influencing factors analysis of the winding end electric field are done by using finite element calculation software.Thus the distribution of main insulation electric field and maximum electric field stress are obtained respectively.Through the comparison of calculation results and the insulation tests of products，the rationality of the calculation methods is examined mutually.Therefore,an efficient analysis method is provided for the insulation design of power transformer.

power transformer；main insulation；electric field（EF）；numerical analysis

TM403.3；TM41

A

1671-024X（2014）03-0075-05

2014-03-10

国家自然科学基金资助项目（51207042）

刘凤英（1961—），女，高级工程师，E-mail：lfy@btw.cn