螺栓连接层合板结构失效模式多尺度数值分析

刘长喜，周振功，张博明，唐占文，王晓宏

(1.哈尔滨工业大学复合材料与结构研究所，150008哈尔滨;2.北京航空航天大学材料科学与工程学院，100191北京; 3.黑龙江工程学院机电工程学院，150030哈尔滨)

机械连接(螺钉或螺栓连接)方式是复合材料层合板结构常用的、重要的连接方式之一，多用于传递较高的载荷，且具有费用低、装配简单，便于拆卸维修等优点;但是，螺栓连接的层合板结构由于其开孔的存在使得承载孔周围产生严重的应力集中现象，应力状态十分复杂，导致结构强度降低，失效模式复杂化、多样化.因此，一直以来，螺栓连接层合板结构的力学性能分析都是该领域内学者们研究的热点.

文献［1-2］采用试验方法研究螺栓孔间隙及试件尺寸等因素对螺栓连接层合板结构的失效模式及强度的影响.文献［3-4］则采用不同的失效准则和刚度衰减模型，分别建立了层合板连接结构的二维及三维模型，对其损伤失效过程进行了数值模拟.文献［5］基于经典层合板理论，建立二维有限元模型，对层合板连接区域的承载能力及破坏模式进行了预测.文献［6-9］也分别采用数值及试验方法对螺栓连接层合板结构的强度进行了分析.

本文针对复合材料本质上是由多种组分材料构成的特点［10］，利用多尺度分析方法，基于有限元软件 ABAQUS及其用户自定义子程序(USDFLD)，引入改进的细观力学模型(GMC模型)，建立考虑细观组分材料性能的螺栓连接层合板结构在双剪切载荷下的宏-细观多尺度数值模型，从细观组分材料的性能出发更加科学合理地揭示复杂应力状态下结构的损伤模式、准确预报其强度性能，并进一步讨论试件几何尺寸对结构的损伤失效模式及其强度的影响，力求为螺栓连接层合板结构的设计与优化提供指导作用.

1 通用单胞模型(GMC模型)

Paley等［11］最早提出通用单胞模型(GMC模型)，主要用于周期性分布纤维复合材料的力学响应预报.传统的GMC模型计算效率非常低，影响其在多尺度力学方面的应用［12］，因此，本文采用改进的GMC模型.

1.1 GMC模型的应用假设

1)纤维周期性分布假设.

服从周期性分布的复合材料可选取代表性单胞来研究其整体性能，如图1所示.

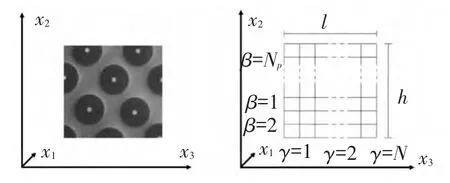
图1 单向复合材料周期性分布和代表性单胞划分

在局部坐标内，将单胞划分成Nβ×Nγ个子胞，每个子胞可单独赋予材料属性，从而进行多相复合材料的细观力学分析.

2)单胞内一阶线性位移假设.

基于该假设，子胞位移可表示为

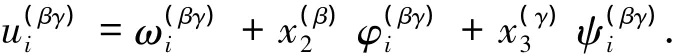
3)体积平均假设.

基于该假设，单胞宏观平均应力、应变表示如下:

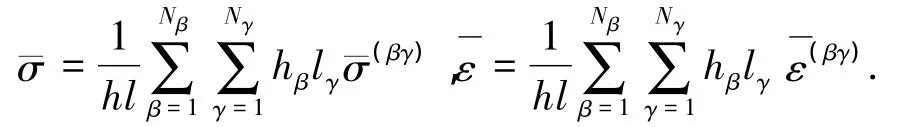
4)子胞界面位移、应力连续假设.

基于该假设，子胞界面位移的连续性表示为

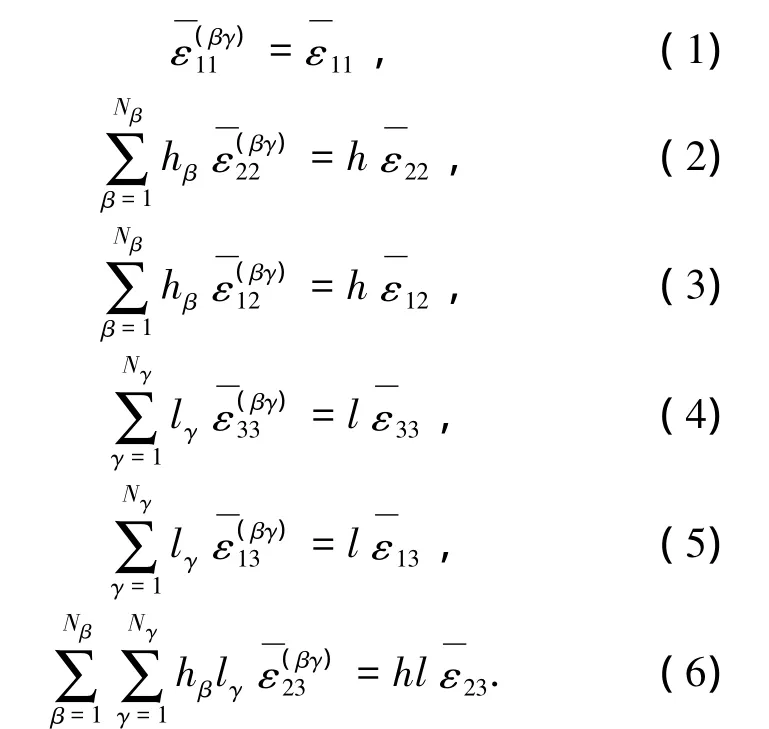
子胞界面应力连续条件为

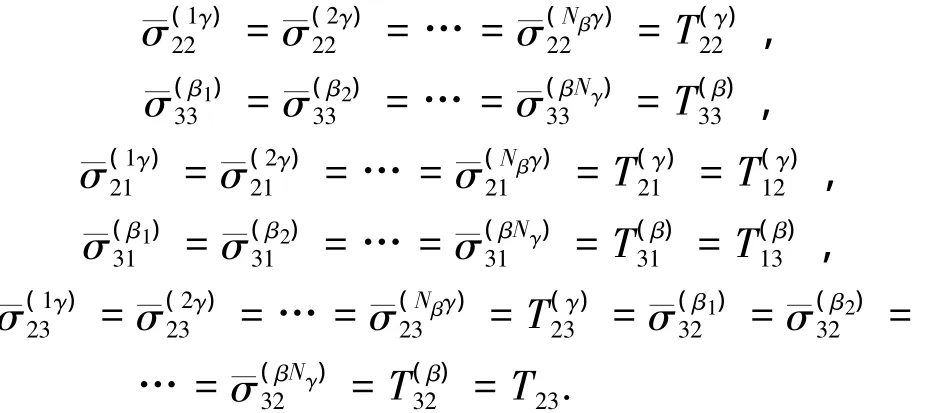
1.2 改进的GMC模型

传统的GMC模型以子胞应变作为基本的细观未知量进行求解，将子胞界面位移连续条件和应力连续条件写成矩阵形式，合并得到子胞应变与宏观应变的关系，如

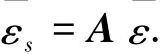
式中矩阵A包含了子胞的几何尺寸、材料性能以及单胞的整体几何尺寸.

最终，获得等效宏观刚度矩阵为

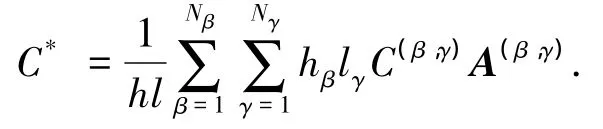
改进的GMC模型以子胞应力作为基本的细观未知量进行求解，大大减少未知量数目，从而提高了计算效率.

根据子胞的本构关系，将子胞应变表示成应力形式为

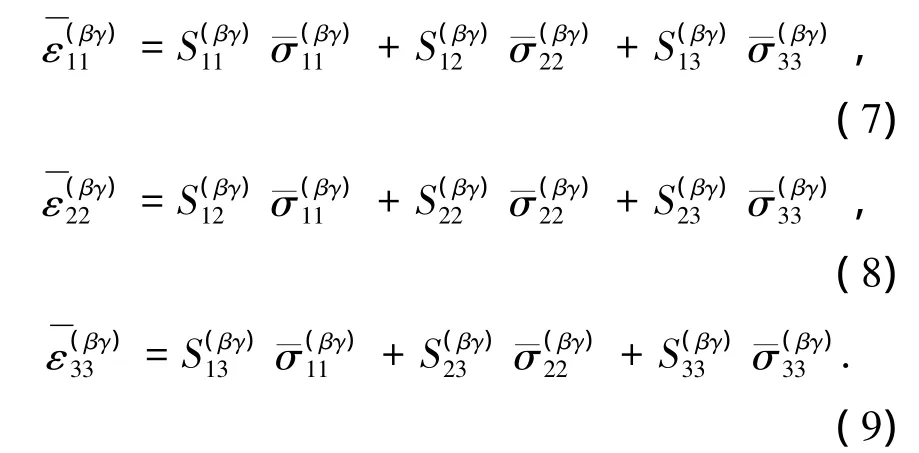
利用各子胞轴向变形相等的边界条件，代入式(7)，得到子胞轴向应力为

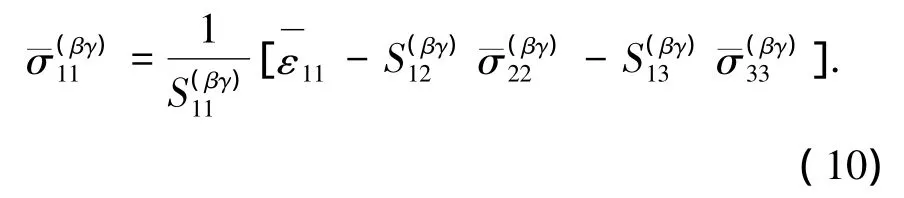
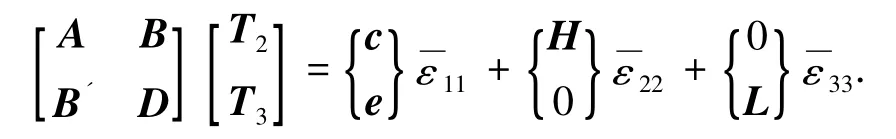
式中:A、B、B'、D分别为Nγ×Nγ，Nγ×Nβ，Nβ× Nγ，Nβ×Nβ阶矩阵;c、e分别为Nβ和Nγ列向量(由子胞几何尺寸和柔度组成).

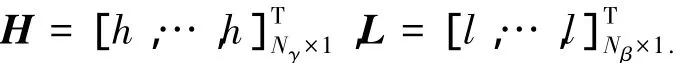
由界面位移连续条件可得横向正应力σ(βγ)22和，由式(10)可得正应力σ(βγ)11.

剪切应力与剪切应变之间的关系推导同上，将式(7)结合本构关系并代入位移连续条件中的式(4)、(5)，即可得到改进的界面位移连续条件，从而求解得到胞的剪切应力分量为

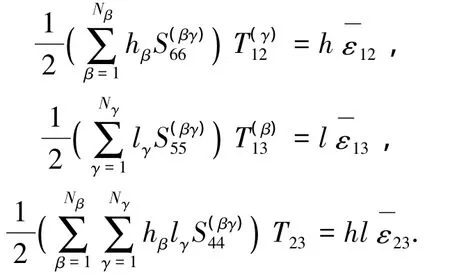
根据体积平均假设，建立单胞宏观平均应力与细观子胞应力的关系为

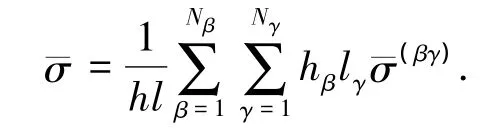
2 宏-细观多尺度数值模型

2.1 基于细观组分的失效准则

充分借鉴文献［13-15］宏观失效判据.本文对于细观组分材料采用如下失效判据(失效判据中的应力及强度分别对应各自组分的应力值和强度)，其表达式如下:

1)基体拉伸(压缩)失效为

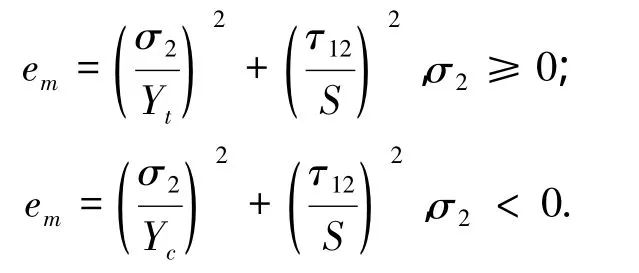
2)纤维拉伸失效为

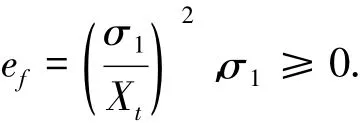
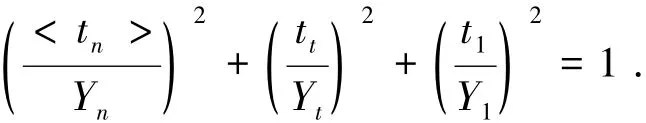
3)纤维-基体界面失效为

2.2 刚度衰减模型

当复合材料各组分材料的细观应力场满足以上任何一个失效判据时，就认为发生了相应的损伤失效，此时需要进行相应的刚度衰减.通常采用的刚度衰减方式主要有两种［16］.本文采用了部分刚度衰减的方式，即当某一层发生损伤的时候，这一层会在某些方向上失去承载能力，而在其他方向上仍具有承载力.相应的刚度衰减与失效状态的对应关系［17-18］如表1所示.

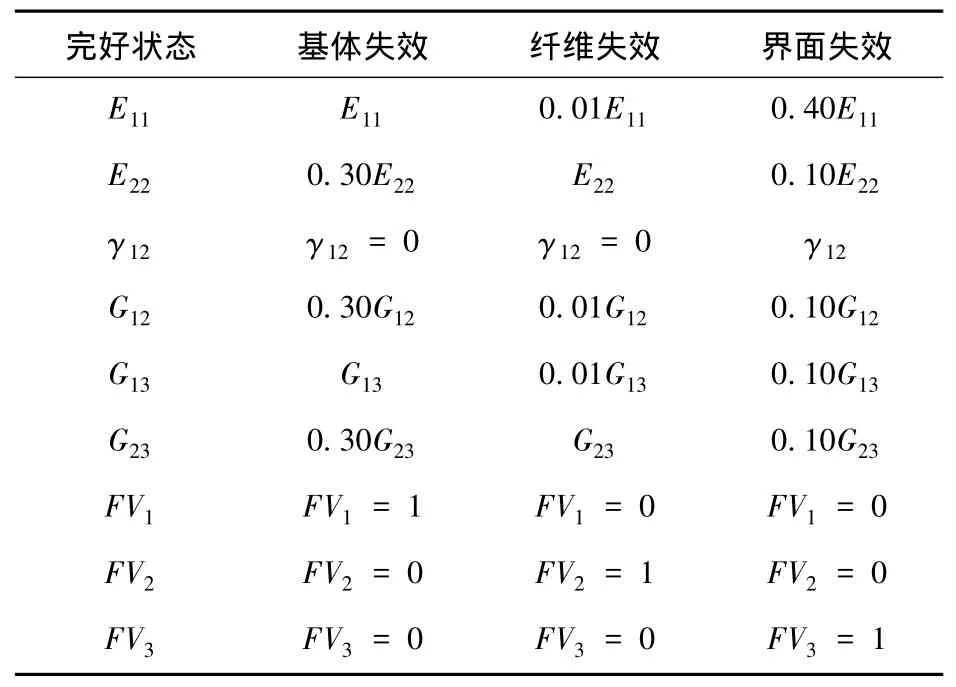
表1 材料性能退化与失效状态的对应关系

2.3 宏－细观多尺度数值分析的实现

利用有限元软件ABAQUS提供的用户自定义子程序(USDFLD)的接口将组分材料(纤维、基体和界面)的失效准则与改进的GMC模型嵌入到螺栓连接层合板结构有限元分析模型，实现考虑细观组分材料损伤/失效的宏-细观多尺度渐进损伤分析和强度预报，基本流程如图2所示.

首先，对结构施加位移载荷，计算得到结构的宏观应力状态;其次，对宏观结构的每个单元调用USDFLD子程序进行细观应力场计算，利用细观组分材料的损伤判据进行损伤/失效判断，如果发生损伤则按表1中的衰减方式进行相应的性能衰减;最后，随着位移载荷的增大，螺栓孔周围的单元不断扭曲变形，当载荷足够大时，计算程序自动中止，已经不能继续增大载荷，此时从载荷-位移曲线上看，载荷已经开始下降，由此可以预测结构的承载能力和失效模式.

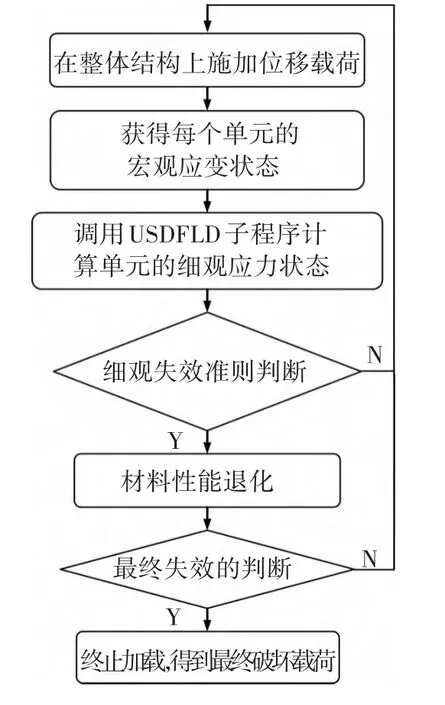
图2 宏－细观多尺度数值分析流程图

2.4 有限元模型

螺栓连接的层合板结构的设计应参考相应的标准(本文参考美国ASTM标准D5961 A)如图3所示.图中:W为层合板宽度，W=36 mm;D为螺栓孔孔径，D=6 mm;E为孔中心距层合板端部距离，E=18 mm;t为厚度，t=3～5 mm;L为层合板长度，L=135 mm，螺栓孔的中心位于层合板对称线上;x为单向板0°铺层方向(纵向);y为单向板90°铺层方向(横向);θ为铺层角度.

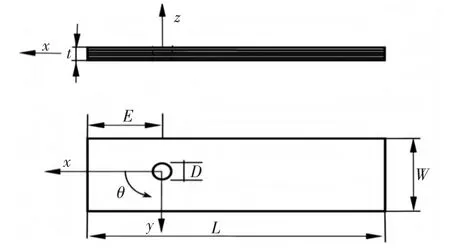
图3 开圆孔单钉连接层合板试件的几何尺寸

根据上述的实验标准，在ABAQUS软件中建立螺栓连接层合板结构在双剪切载荷作用下的有限元模型.试件采用实体壳单元沿厚度方向利用扫掠方式进行网格划分;夹具视为刚体.螺栓与试件孔之间采用基于小滑动摩擦的主-从平面接触算法，由于实际应用中的螺栓刚度一般比较大，且文献［19］中指出螺栓的刚度对螺栓孔周围应力的影响很小，所以模型中螺栓采用刚体模拟，使得计算效率提高且更易于结果收敛，有限元模型如图4所示.

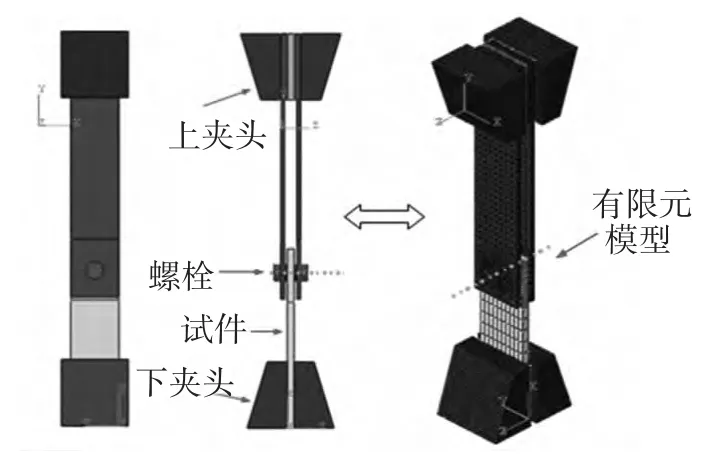
图4 螺栓连接层合板结构双剪切载荷作用下的有限元模型

2.5 模拟结果与分析

计算所用材料的性能参数如表2所示，层合板试件的几何尺寸以及铺层方式详见文献［18］.

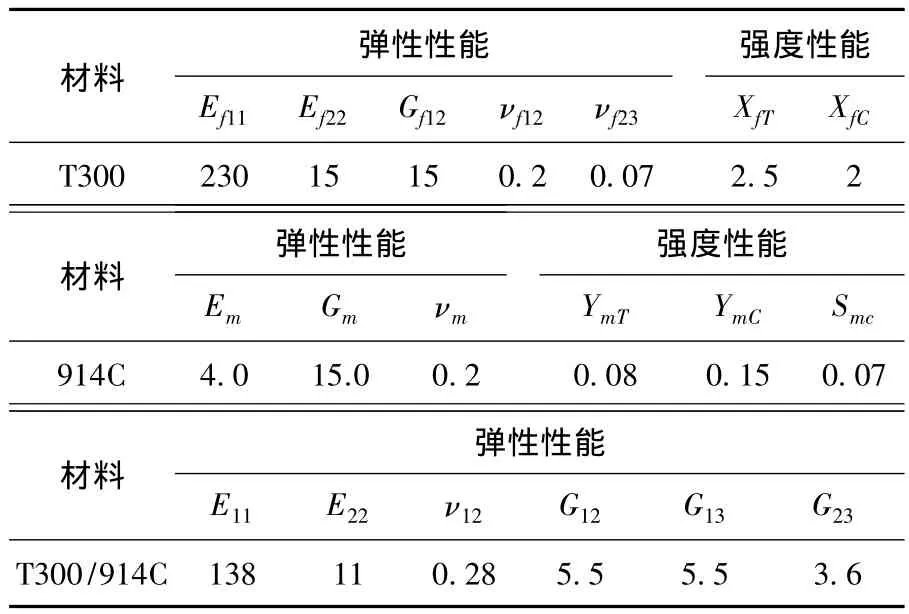
表2 T300/914C epoxy材料性能参数 GPa

基于上述有限元模型对螺栓连接的层合板结构在双剪切载荷作用时出现的典型损伤模式(净拉伸损伤模式、剪出损伤模式、挤压损伤模式)进行模拟预报并与文献［19］进行对比，结果如图5所示.由图5可以看出，本文所建立的数值模型对不同铺层形式的螺栓连接层合板结构在双剪切拉伸载荷下损伤模式的模拟预报结果与文献［18］中的实验结果基本吻合，初步证明本文所建立宏-细观多尺度数值模型的有效性.

基于上述建立的数值模型，进一步预报螺栓连接层合板结构的极限挤压强度.螺栓连接层合板结构极限挤压强度的定义为

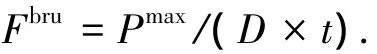
式中:Fbru为极限挤压强度，MPa;Pmax为破坏前最大载荷，N;D为孔直径，mm;t为厚度，mm;

实验中所用试件的材料性能如表2所示，铺层形式为［0/45/90］s，端径比E/D=2，宽径比W/D=3.预报结果与实验结果对比如图6所示.

由图6可知，［0/45/90］s铺层的螺栓连接层合板结构极限挤压强度的预报结果(892.7 MPa)与实验结果(868.4 MPa)基本一致，误差为2.7%.进一步证明了模型的适用性，可用于进一步的分析.

2.6 试件几何尺寸对损伤模式的影响

首先，改变试件的几何尺寸(表3)，研究其对螺栓连接层合板结构在双剪切载荷作用下损伤模式的影响，如图7所示.

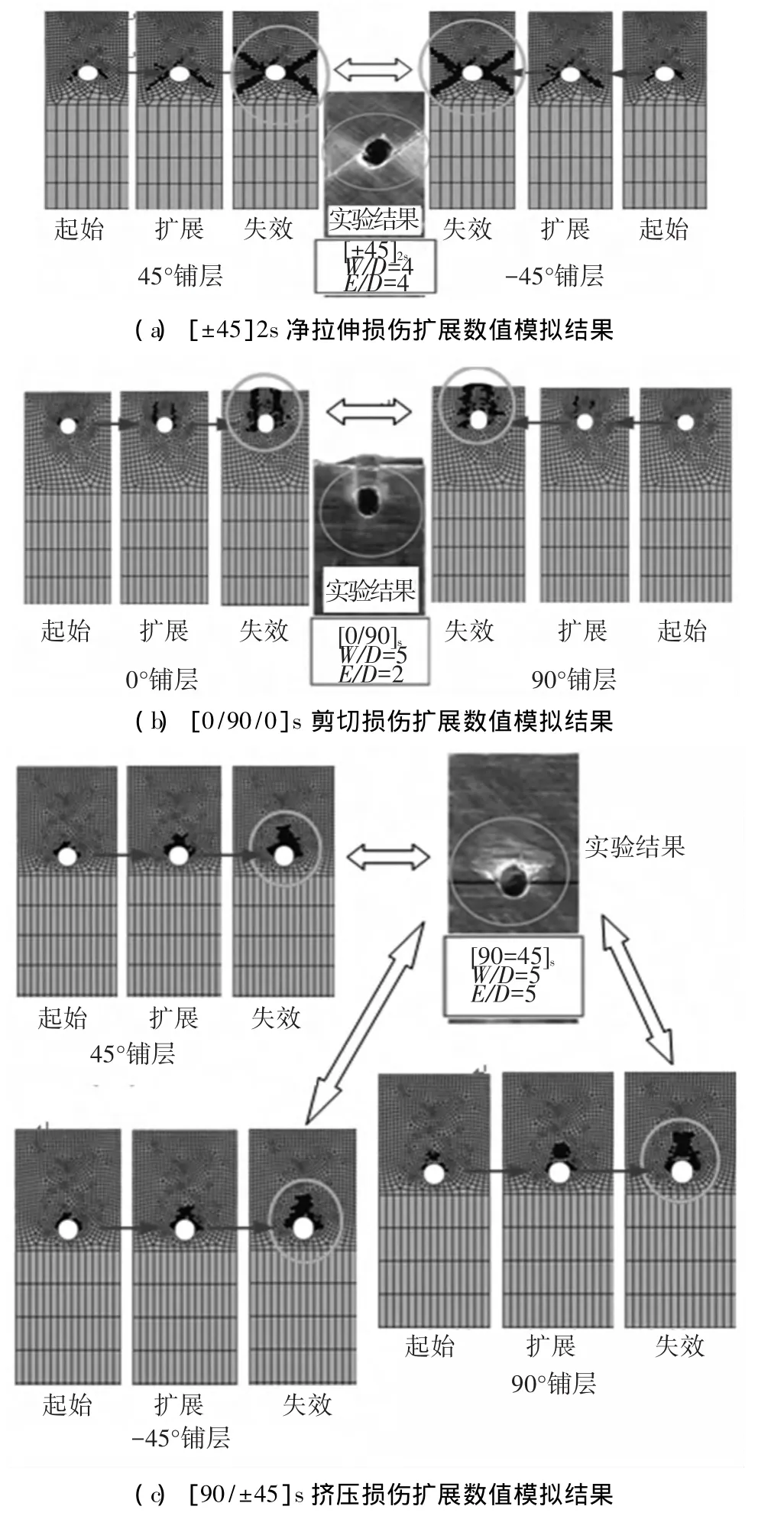
图5 不同铺层形式的层合板损伤扩展预报结果

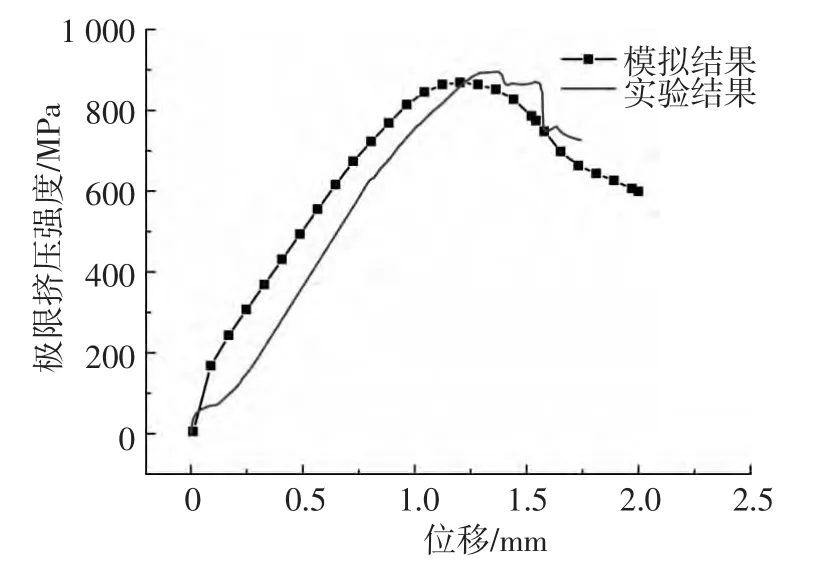
图6 ［0/45/90］s螺栓连接层合板结构的极限挤压强度预报结果与实验结果对比

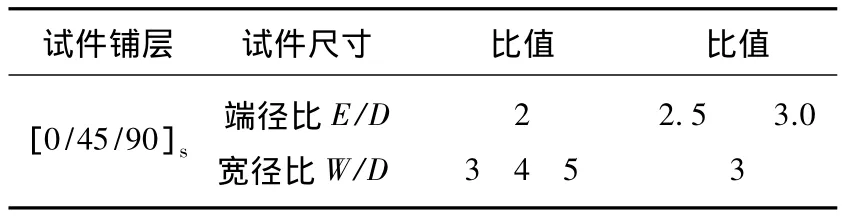
表3 试件尺寸变化

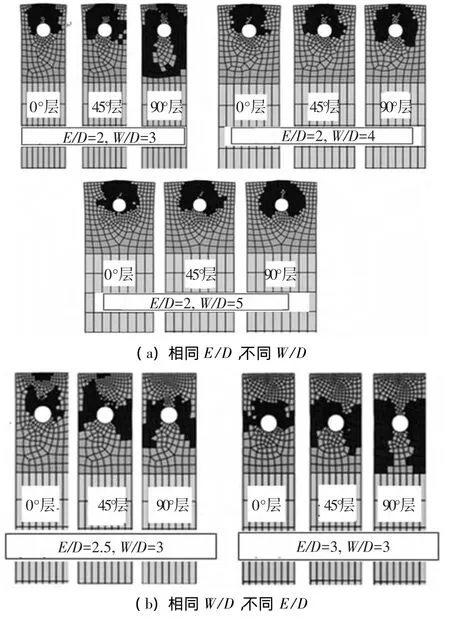
图7 试件几何尺寸对损伤模式的影响

由图7可知，E/D=3，W/D=3试件在双剪切载荷下的破坏模式以挤压-拉伸组合破坏为主，并主要是拉伸破坏;E/D=2，W/D=5试件的破坏模式以挤压-剪切组合破坏为主，其中挤压破坏形式更加显著.随着试件几何尺寸的改变，螺栓连接层合板结构在双剪切载荷下的损伤模式有:当层合板接头端径比(E/D)不变时，随着层合板宽径比(W/D)在一定范围内的增加，试件的破坏模式从以净拉伸形式破坏逐渐过渡到以剪切形式破坏为主;当层合板宽径比较小的时候(W/D＜4)，层合板端径比(E/D)在一定范围内的增加，试件的破坏模式均以拉伸(剪切)破坏为主，但是当宽径比较大的时候(W/D≥4)，随着层合板端径比(E/D)的增加，其破坏模式逐步过渡到以挤压破坏为主.

2.7 试件几何尺寸对极限挤压强度的影响

改变试件的几何尺寸(表3)，研究其对螺栓连接层合板结构挤压静强度的影响，如图8所示.

由图8(a)可知，当端径比(E/D)固定时，宽径比(W/D)的改变对结构的极限压缩强度影响较大，随着W/D的增加极限压缩强度增加幅度较大.所以，工程实际应用中螺钉(螺栓)连接层合板结构的设计一定要合理考虑W/D.由图8(b)可知，当宽径比(W/D)固定时，端径比(E/D)的改变对结构的极限压缩强度影响不大，随着E/D的减小极限挤压强度略有减小.但E/D对曲线的下降阶段会产生一些影响，E/D较大时，曲线下降的较快，即挤压强度明显降低.

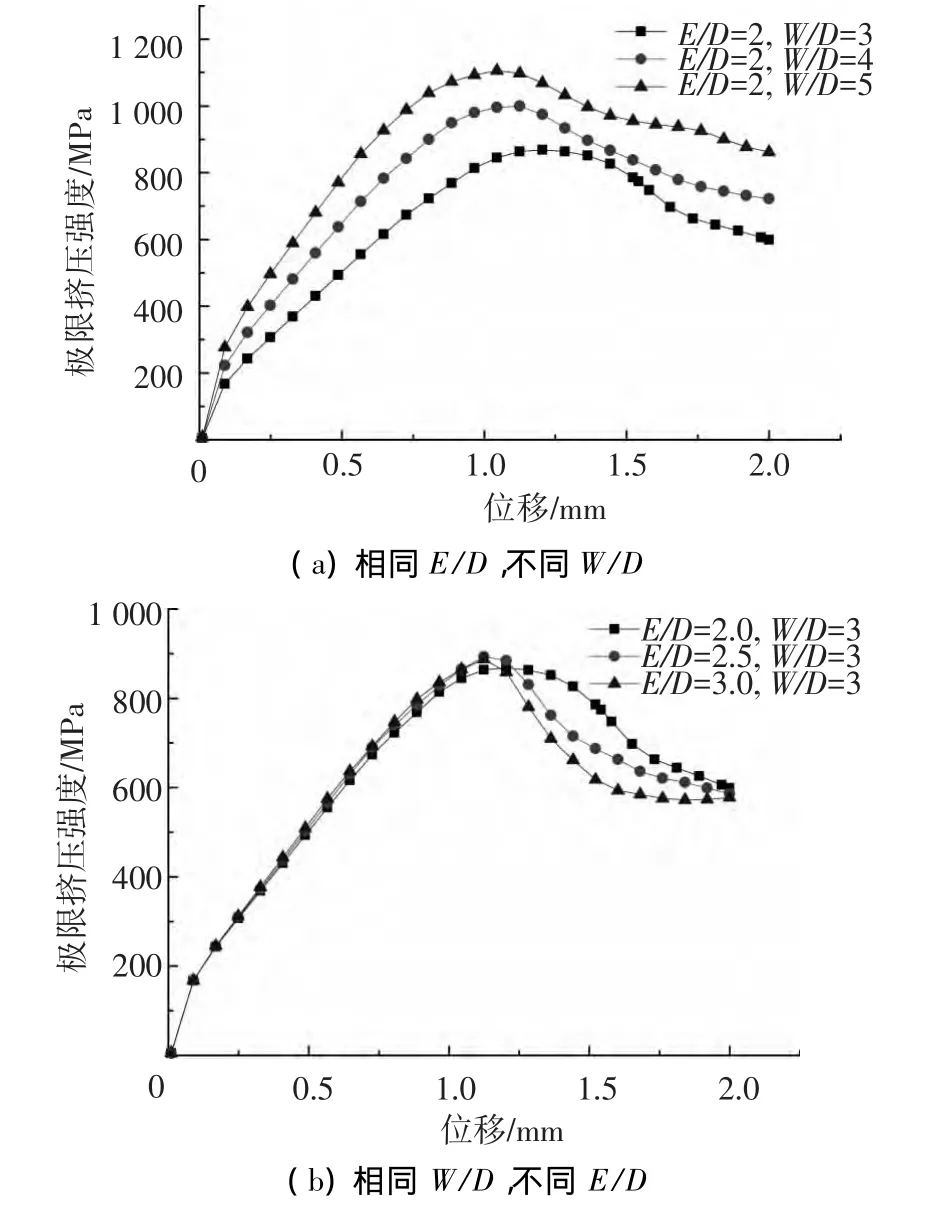
图8 试件几何尺寸对极限挤压强度的影响

3 结论

1)螺栓连接层合板结构在双剪切载荷作用下损伤模式的预报结果与文献中结果吻合较好，强度预报结果与实验值基本一致，充分证明本文建立的多尺度数值模型的有效性.

2)试件几何尺寸的改变对螺栓连接层合板结构的损伤模式及挤压强度均存在一定的影响，尤其是结构中宽径比(W/D)的变化对结构的挤压强度影响较大，在设计过程中应给予充分的考虑.

［1］KELLY G，HALLSTROM S.Bearing strength of carbon fiber/epoxy laminates:effects of bolt-hole clearance［J］. Composites Part B:Engineering，2004，35(4):331-343.

［2］OKUTAN B.The effects of geometric paramet ers on the failure strength for pinloaded multi-directional fiber glass reinforced epoxy laminate［J］.Composites Part B: Engineering，2002，33(8):567-578.

［3］DANO M L，GENDRON G，PICARD A.Stress and failure analysisofmechanically fastened jointsin composites laminates［J］.Composite Structures，2000， 50(3):287-296.

［4］TSERPES K I，PAPANIKOS P，KERMANIDIS T H.A three-dimensional progressive damage model for bolted joints in composite laminates subjected to tensile loading［J］.Fatigue＆Fracture of Engineering Materials＆Structures，2001，24(10):663-675.

［5］陈浩然，马保国，关长文.纤维增强复合材料层合板螺栓连接区强度预测［J］.强度与环境，1988(1): 28-35.

［6］姜云鹏，岳珠峰.复合材料层合板螺栓连接失效的数值模拟［J］.复合材料学报，2005，22(4):177-182.

［7］王佩艳，朱振涛，王富生，等.复合材料螺栓连接性能的分散性和可靠性分析［J］.力学季刊，2008，29(4):573-577.

［8］黄金昌，王晓冬.复合材料夹层连接螺栓拧紧力矩试验研究［J］.飞机设计，2009，29(4):32-35.

［9］王晓侠，方超，张亮，等.复合材料层合板螺栓连接强度试验研究［J］.中国舰船研究，2011，6(3):88-93.

［10］CAMANHO P P，MATTHEWS F L.A progressive damage modelformechanically fastened jointsin composite laminates［J］. Journal of Composite Materials，1999，33(24):2248-2280.

［11］PALEY M，ABOUDI J.Micromechanical analysis of composites by the generalized cellsmodel［J］. Mechanics of Materials，1992，14(2):127-139.

［12］GOTSISA P K，CHAMISA C C，MINNETYANB L. Prediction of composite laminate fracture:micromechanics and progressive fracture［J］.Composites Science and Technology，1998，58(7):1137-1149.

［13］HILL R.A theory of the yielding and plastic flow of anisotropic metals［J］.Proceedings of the Royal Society of London.Series A，1948，193(1033):281-297.

［14］TSAI S W，WU E M.A general theory of strength for anisotropic materials［J］. Journal of Composite Materials，1971，5(1):58-80.

［15］HOFFMAN O.The Brittle Strength of Orthotropic Materials［J］.Journal of Composite Materials，1967，1(2):200-206.

［16］蔡为仑(美).复合材料设计［M］.刘方龙等，译.北京:科学出版社，1988.

［17］李伟占.复合材料层合板损伤失效模拟分析［D］.哈尔滨:哈尔滨工程大学，2012.

［18］BABA B O.Behavior of pin-loaded laminated composites［J］.Experimental Mechanics，2006，46(5):589-600.

［19］HYER M W，KLANG E C，COOPER D E.The effect of pin elasticity，clearance and friction on the stresses in a pin-load orthotropic plate［J］.Journal of Composite Materials March，1987，21(3):190-206.