一种改进的变参数粒子群算法
檀蕊莲,柏 鹏,李 哲,卢 虎,王 澈
(1.西安武警工程大学,陕西西安710086;2.空军工程大学,陕西 西安710051)
粒子群优化算法(PSO)是由美国电气工程师Eberhart和社会心理学家Kennedy基于群鸟觅食提出来的一种智能算法[1-2]。由于该算法算法简单、所需参数少、易于实现等优点从而广泛应用于科学和工程领域[3-4]。由于算法参数较少,也使得其容易陷入局部最优和维数灾难。针对这些问题,尤其是针对算法参数调整方面,相关学者针提出了很多改进算法[5-7]。其中,Shi和Eberhart最早引入了惯性权重的概念[5],即后来普遍认为的标准粒子群算法(SPSO),这也为后续学者在参数调整方面的研究奠定了基础;Clerc提出一种带收缩因子的粒子群算法(CPSO)[6],使用收缩因子可以通过平衡局部开发能力与全局搜索能力从而改善粒子群算法收敛性能。然而,对于如何寻求更合适该算法的参数问题仍然是研究的重点和难点。本文在前人研究的基础上,提出了一种新的参数调整方案,将SPSO算法和CPSO算法的精华部分进行融合,根据粒子运动的特点进行参数调整,对速度更新公式各项配以相应的权重因子,从而提高了算法的寻优性能。对三个基准函数进行测试,并与已有SPSO算法和CPSO算法进行对比,证明了本文所提算法在寻优精度和执行性能方面都具有较好的性能,在求解高维函数优化问题时亦能有效避免维数灾难。
1 标准粒子群算法
假设由m个粒子组成种群X=(X1,X2,…,Xm),则在一个d维的搜索空间中,问题的一个可能解即为第i个粒子在d维搜索空间的位置向量 Xi=(Xi1,Xi2,…,Xid)T。若以Pi=(Pi1,Pi2,…,Pid)T代表粒子i所经历的最好位置,Pg=(Pg1,Pg2,…,Pgd)T代表种群的全局最优位置,Vi=(Vi1,Vi2,…,Vid)T代表第i个粒子在d维空间的飞行速度,则在每次迭代过程中,粒子将按式(1)、式(2)更新自身的速度和位置

式中:ω为惯性权重;i=1,2…,n;Vid为粒子的速度;c1和c2称为加速因子,通常取2.0;r1和r2为均匀分布的随机数,分布于[0,1]之间。加入惯性权重ω的PSO算法即为标准粒子群算法(SPSO),由于其参数较少,操作简单,寻优效果较好而得到广泛应用。按照Shi和Eberhart最早提出的概念,惯性权重ω按式(3)线性递减

式中:ωstart为初始惯性权重;ωend为迭代到最大次数时的惯性权重;k为当前迭代次数;Kmax为最大迭代次数。然而,SPSO算法可调整参数过少,使得该算法的数学基础相对薄弱,当面对非线性函数或者是多维函数的优化问题时,往往过早陷入局部最优,寻优效果并不理想。
2 改进的PSO算法
2.1 带约束因子的PSO算法
Clerc提出的带收缩因子的粒子群算法(CPSO)定义如下

式中:CPSO 算法中Clerc设定l=4.1,c1=c2=2.05,则收缩因子 χ为 0.729,后两项系数为 0.729 × 2.05ri=1.494 45ri,相当于速度跟新公式中所有的项都乘一样的权重因子,并未考虑到各个项的单独作用,虽然算法在收敛性方面有所改善,但是必须预先对算法进行限定,而且必须针对一定的函数,否则在给定的迭代次数下很难找到全局最优,应用范围受限。
2.2 改进的PSO算法
如何选取合适的参数从而使得算法具有更好的收敛性是研究的热点和难点,迭代初期本文期望得到较大的惯性权重使得算法保存较强的全局搜索能力,而迭代后期则期望得到较小的惯性权重,有利于算法进行更精确的局部搜索。文献[6]指出通过设定约束因子可以得到更好的收敛性能,然而实际上期望的是在全局最优位置一定的情况下粒子的个体最优位置更新得更快,从而使得算法的局部搜索能力与全局搜索能力相平衡,达到更好的寻优效果。综合SPSO和CPSO的优缺点,本文提出一种新的参数调整策略,速度更新公式各项配以不同的权重因子。其表达式如下
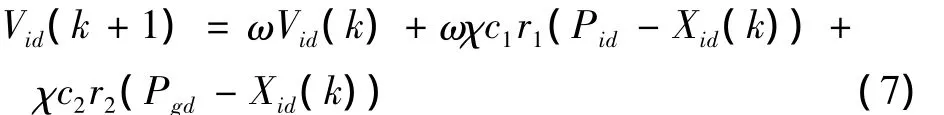
式(7)第一部分是对当前速度的调整,后两部分是对粒子个体与全局位置的调整。式(7)第一部分保持SPSO算法的惯性权重因子,可以使得粒子搜索速度加快;第三部分保持CPSO算法的约束因子,可以保证粒子具有更好的全局寻优性能;第二部分则融入了SPSO算法和CPSO算法的精华部分,权重因子为惯性权重因子与约束因子相乘,既达到了约束的目的,又可以保证粒子个体更新按前期速度加速更新,从而使得个体寻优和全局寻优达到平衡。
2.3 算法实现
步骤1:初始化参数。设置惯性权重ω的取值范围,随机因子r1和r2,最大迭代次数Kmax,初始速度Vid,空间维数D,并在所定义的搜索空间中随机生成m个粒子组成初始种群。
步骤2:计算种群中每个粒子的适应度函数值。
步骤3:根据式(7)更新各粒子的飞行速度,根据更新的飞行速度按照式(2)更新各粒子的位置,从而产生新的种群,实现个体极值和群体极值的更新。
步骤4:判断是否满足终止条件,若满足,则算法结束,输出最优解;否则转入步骤2,直到达到最大迭代次数才终止。
3 仿真实验及性能分析
3.1 测试函数
为检验本文所提算法的性能,选择3个较常用于测试优化算法性能的基准函数进行测试,各个测试函数的表达式及其搜索空间如表1所示。其中,Sphere函数为非线性对称单峰函数,极易实现,主要用于测试算法的寻优精度;Rosenbrock函数是很难极小化的病态二次函数,主要用于评价优化算法的执行性能;Rastrigrin函数为典型的具有大量局部最优点的复杂多峰函数,极易陷入局部最优,主要用于测试算法的局部寻优能力,3个基准测试函数的最优解均为0。

表1 测试函数
3.2 仿真结果与分析
粒子种群规模分别取20,40,60;最大迭代次数在维数为10,20,30 维时分别对应300,600,900 次;惯性权重ωstart=0.9,ωend=0.4;每个基准测试函数独立在SPSO 算法,CPSO算法,本文算法中各运行100次,分别求出最小适应度函数的平均值最优值作为评价标准。表2~表4为各基准函数在这3种算法中的测试结果。

表2 Sphere函数平均最优解比较

表3 Rosenbrock函数平均最优解比较

表4 Rastrigrin函数平均最优解比较
由表2数据对比可以看出,在对单峰函数f1(x)的优化中,当种群规模为20时,空间维数较小则3种算法的平均最优解都接近于理论最优解,随着空间维数和迭代次数的增加,寻优难度相应增大,本文算法在相同空间维数和迭代次数下取得了更接近理论最优值的数值,随着种群规模的增加到60,本文算法比SPSO算法和CPSO算法的最优解低了一个数量级,证明本文算法在求解多维函数时具有更好的寻优精度。
由表3数据对比可以看出,虽然f2(x)为很难极小化的病态二次函数,但是当空间维数较小时,本文算法相较于SPSO算法和CPSO算法,寻优结果更贴近与理论最优值,当空间维数由10增加到30,本文算法也表现出更好的寻优性能,随着种群规模的增加,寻优精度更好,证明本文算法在求解多维函数时具有更好的寻优执行能力。
由表4数据对比可以看出,对于具有大量局部最优点的复杂多峰函数,CPSO算法在空间维数增加时局部寻优能力逐渐变弱,而SPSO算法在种群规模增加时寻优结果变动不大,证明极有可能以及陷入局部最优而无法跳出,而本文所提算法则随着种群规模的增加取得了更好的寻优数值,证明本文所提算法在求解多维函数时局部寻优能力更强,整体性能更好。
为了更直观反映算法的寻优效果,将SPSO、CPSO和本文算法在粒子种群规模为60,解空间为30维时进行比较,3种算法对测试函数的收敛曲线如图1所示。由图1可见,本文算法在解决多维函数优化问题时亦能取得较好的收敛性能,有效避免了维数灾难,再次证明了本文所提算法的有效性。
4 结语
本文提出了一种改进的变参数粒子群算法,该算法在SPSO算法和CPSO算法的基础上做出改进,融合二者的精华部分,将速度更新公式做各项根据其运动特性配以不同的权重因子,算法操作简单,易于实现。通过3个基准测试函数的仿真结果表明,本文所提算法具有更好的寻优精度和执行能力,在求解多维函数优化问题时,亦能表现出优越的收敛性能。
[1]PEREZ R,BEHDINAN K.Particle swarm approach for structural design optimization[J]. Computers & Structures,2007,85(19/20):1579-1588.
[2]COELHO L,SIERAKOWSKI C.A software tool for teaching of particle swarm optimization fundamentals[J].Advances in Engineering Software,2008,39(11):877-887.
[3]FAN S,ZAHARA E.A hybrid simplex search and particle swarm optimization for unconstrained optimization[J].European Journal of Operational Research,2007,181(2):527-548.
[4]LI X.Niching without niching paramenters:particle swarm optimization using a ring topology[J].IEEE Trans.Evolutionary Computation,2010,14(1):150-169.
[5]SHI Y,EBERHART R.A modified particle swarm optimizer[C]//Proc.IEEE Enternational Conference on Evolutionary Computation.Anchorage,AK:IEEE Press,1998:69-73.
[6]CLERC M.The swarm and the queen:towards a deterministic and adaptive particle swarm optimization[C]//Proc.Congress of Evolutionary Computation.Washington:IEEE Press,1999:1951-1957.
[7]李殷,李飞.基于量子粒子群优化算法的图像矢量量化码书设计[J].电视技术,2012,36(17):54-56.

