图约束字典和加权稀疏表示人脸超分辨率算法
黄克斌,胡瑞敏,王 锋,韩 镇,卢 涛,江俊君
(1.黄冈师范学院数字媒体技术系,湖北黄冈438000;2.武汉大学国家多媒体软件工程技术研究中心,湖北武汉430072)
视频监控具有实时、可视、可记录及信息量大等特点,在安防、交通、生产管理等各应用领域发挥重大作用。监控视频中的人脸图像是辨识关键人物最直接的线索。但是在实际监控应用中,由于摄像头和人脸距离通常较远,视频监控系统的带宽和存储资源有限等原因,往往导致监控视频中人脸图像的分辨率较低,难以达到辨识要求。人脸超分辨率技术也叫做人脸幻象技术(Face Hallucination)[1],它能够在不改变硬件环境的情况下,从一幅或多幅低分辨率输入人脸图像中,重建出一幅高分辨率的人脸图像,达到改善人脸图像的清晰度的目的。该技术在安防监控、计算机视觉等领域中具有重要的应用。
自Baker和Ce Liu等人提出“人脸幻象”的概念之后,人脸超分辨率的研究就受到了广泛的关注,出现了一系列的人脸超分辨率算法,如基于子空间的方法[2-4]、基于流形的方法[5-6]和基于稀疏表示的方法[7-9]等。本研究中主要关注基于稀疏表示的人脸超分辨率方法。
稀疏表示(Sparse Representation)被认为是一种新型、有效而且鲁棒的特征表示方式,成功地应用于一系列实际问题中,是目前最热门的研究课题之一[10]。Yang等首次将压缩感知的思想应用到超分辨率领域,提出了基于稀疏表示的自然图像超分辨率算法[7]。该方法充分利用稀疏表示符合人眼感知特性的优势,自动选取近邻个数,避免了人为指定近邻块个数会导致合成信息不足或过拟合的弊端,取得了较好的超分辨率效果。在Yang的基础上,Chang等提出基于稀疏表示和双字典学习的人脸素描图像合成方法[8],Jung等提出了基于稀疏表示和原始样本块字典的人脸超分辨率算法[9]。
尽管基于稀疏表示的人脸超分辨率方法比其他方法取得了更好的效果,但是,已有的基于稀疏表示的方法较少考虑样本数据内在的几何结构,这影响了冗余字典的表达能力。最近研究表明,保持数据内部的局部拓扑结构能有效改善稀疏编码的效果[11-13]。因此,本文提出了一种基于图约束字典和加权稀疏表示的人脸超分辨率算法,算法包括训练和重建两个阶段。在训练阶段,三方面措施被用于提高冗余字典的表达能力:一是利用人脸的位置信息对样本进行聚类,保持人脸块的全局信息;二是利用图约束稀疏编码进行字典的学习,保持人脸块的局部信息;三是利用联合训练高低分辨率冗余字典,保持高低分辨率字典对在内部流形结构上的一致性。在重建阶段,加权稀疏编码均值被用于消除超分辨率重建过程中的稀疏编码噪声,以提高高分辨率人脸图像重建系数的精度。实验结果证明了该方法的有效性。
1 图约束稀疏编码
1.1 图的构建
谱图理论[14]和流形学习理论[13]的研究表明,散布点的局部几何结构可以通过近邻图进行有效地建模。这里简要介绍近邻图的构建过程。
假设 X= [x1,x2,…,xN]∈ RM×Q是一个数据集,M表示数据维数,Q表示数据集中元素的个数。基于数据集X构建的图表示为G=(V,W),其中,V=Q表示该图中顶点的个数,每个数据点作为图的一个顶点。每两个顶点之间用无向边 wi,j连接,wi,j表示顶点 i和顶点 j之间的相似性,则数据集 X 的权重矩阵表示为 W= [wi,j]Q×Q。计算顶点之间权重的方法主要有三种,分别是:0-1权重法、热核权重法和点积权重法[12]。由于热核权重法更适合于图像处理,这里采用热核权重法计算顶点之间的相似性权重。欧几里德距离空间的热核权重表示为

式中:h为常数,h>0,其值取决于期望的稀疏编码系数权重的分布幅度,期望的稀疏编码系数权重的分布幅度大,则h取值大;ci为归一化。权重矩阵W表示为

式中:Nk(xi)表示数据点xi的K近邻数据集合。权重矩阵W包含了整个数据空间的几何结构信息。基于以上图模型,将每个人脸图像块作为一个数据点,从而可以实现训练样本库的几何图的构建。
1.2 图约束稀疏编码
假设 X= [x1,x2,…,xN]∈ RM×Q表示原始数据矩阵,D= [d1,d2,…,dL]∈ RM×L表示字典矩阵,S= [s1,s2,…,sN]∈RL×Q表示数据集X在字典D上的稀疏编码系数矩阵。对数据集X进行稀疏编码的目的在于找到一个字典矩阵D和一个稀疏系数矩阵S,使得二者的乘积能够尽可能地逼近原始数据矩阵。稀疏编码的目标函数表示为

式中:第一项为逼近误差项;第二项为稀疏性约束项;λ为正则化参数,用于平衡逼近误差和稀疏性之间的权重。
为了实现原始数据集内部的几何图结构向稀疏编码系数空间的映射,通常假设在欧几里德距离空间近邻的两个原始数据点xi和xj,在稀疏编码系数空间的表示系数si和sj也是近邻的。该假设得到了大量实践的验证[11-13]。因此,K近邻图约束可以表示为
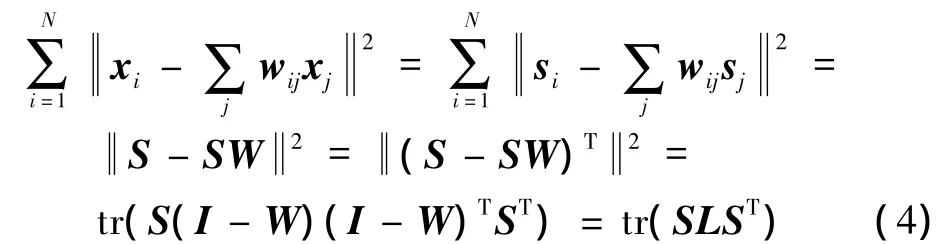
式中:I为单元矩阵;L=(I-W)(I-W)T。将K近邻图约束结合到原始的稀疏编码框架中,新的优化问题可以表示为
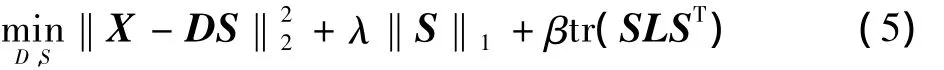
式中:常数β用于平衡K近邻图约束项在优化过程中的比重。式(5)同时拥有两个变量D和S,是一个非凸优化问题,无法正常求解。对上式通常采用迭代方法求解,即先固定一个变量,求解另一个变量。
2 基于图约束字典和加权稀疏表示的人脸超分辨率算法
2.1 图约束位置块字典的学习
由于人脸较之自然图像更具有规则性。人脸图像分块的位置,如眼睛、鼻子、嘴等,包含了人脸图像重建的先验信息。因此,在构建学习字典的过程中,首先根据位置信息,对人脸图像分块进行聚类。同一位置上的分块作为一个训练集。
假设 I={I}Q= [I,I,…,I]∈ RM×Q和HH,qq=1H,1H,2H,Q分别表示对应的高低分辨率训练图像集矩阵,矩阵的列数Q表示训练图像数量,矩阵的行数M、N分别表示高低分辨率图像向量的维数,其中M=s2N,s表示下采样的倍数。训练集中的每幅图像分割成P个小块。根据人脸图像的位置信息,所有的训练块可以分为P个集合。高分辨率训练块集合表示为{I1}Q,{I2}Q,…,{IP}Q,低分辨率训练块集合表示为{I1}Q,{I2}Q,…,{IP}Q。由于L,qq=1L,qq=1L,qq=1人脸图像事先进行了对齐操作,相同位置块集合能提供更多的重建信息。
对于给定的位置P,对应的高、低分辨率块集合IpH={IpH,q|1≤q≤Q}和IpL={IpL,q|1≤q≤Q}被用于训练高、低分辨率字典DpH和DpL。基于图约束位置块的高、低分辨率字典分别可以通过式(6)、式(7)得到

为了保持高、低分辨率字典DpH和DpL中高、低分辨率图像块之间的映射关系,这里采用联合字典学习方法进行字典对的学习。通过联合字典学习,只需一次稀疏分解,可以同时训练得到高、低分辨率两个字典,并且两个字典共享相同的稀疏编码系数。图约束联合字典对学习的目标函数如下

因此,高、低分辨率训练样本集可以表示为IpH=DpHS和IpL=DpLS。采用图约束位置块联合字典对训练,保证了SH和SL的一致性。
2.2 重建系数的优化求解
在图像超分辨率场景下,通常假设高低分辨率图像块拥有同样的稀疏编码系数。因此,低分辨率图像块的稀疏编码系数可以被映射到高分辨率图像块字典上,从而生成高分辨率图像块,即

然而,实际超分辨率应用中,高、低分辨率图像块的稀疏编码系数并不完全一致,之间存在稀疏编码噪声σS=SH-SL。通过抑制稀疏编码噪声,可以提高重建过程中,高、低分辨率编码系数的一致性,即可提高超分辨率图像重建的精确度。因此,在求解输入低分辨率图像块的稀疏编码系数时,可以加入稀疏编码噪声约束以提高重建系数求解的精确度。优化重建系数求解的目标函数为

式中:γ是正则化常量;lp范数用于表示SH和SL之间的距离。由于SH是未知的,因此,稀疏编码噪声无法直接计算。文献[9]提出了利用SH的稀疏编码均值E[SHN(k)]表示SH的思路。假设稀疏编码噪声近似于零均值随机变量,那么高、低分辨率图像块的稀疏编码均值非常接近,即。式(10)可表示为

这里采用加权的K近邻块的稀疏编码均值来表示E[SLN(p)],距离越远的近邻块,权重越小,反之,权值越大。输入图像块的K近邻稀疏编码均值,采用以下公式计算获得

式中:Sp,k是第 k个近邻块的稀疏编码系数;ωp,k是第 k个近邻块的稀疏编码系数的权重;Np表示图像块p的K近邻块组成的集合,k∈Np。
2.3 基于图约束字典和加权稀疏表示的人脸超分辨率算法
本算法主要包括字典学习和高分辨率图像重建两个阶段。前者是离线完成,得到一系列高低分辨率人脸图像块冗余字典对;后者是在线完成,通过将重建高分辨率图像块进行交叠融合,得到最终的高分辨率人脸图像。整个算法过程表示如下。
1)离线训练阶段
(1)输入训练集IH,IL,正则化参数λ,β。
(2)构建相似矩阵W,矩阵中的元素定义如下

(3)计算矩阵

(4)联合训练过完备字典对

(5)重复(2)~(4),获取所有位置的字典对序列。
(6)输出高、低分辨率字典对序列

2)在线重建阶段
(1)输入高、低分辨率字典对序列

测试图像IT,正则化参数λ,γ。
(2)For each LR patch IpTfrom IT
计算输入图像块IpT的K近邻稀疏编码均值;计算输入图像块IpT的稀疏编码系数;生成高分辨率图像块I*pT=DpHSp。
(3)End for。
(4)交叠生成的高分辨率图像块,得到最终高分辨图像块I*T。
(5)输出高分辨率图像I*T。
3 实验结果及分析
采用MATLAB 7.8(R2009a)作为仿真实验平台在PC 机上(双核3.20 GHz CPU,4 Gbyte RAM ,Windows7 操作系统)实现了提出的算法。实验中,采用AR[15]人脸数据库作为训练和测试图像。AR数据库有4 000多张正面人脸图像组成,分别来自126个人,其中,男性70人、女性56人,每个人获取26张不同表情、不同照度和不同遮挡程度的图像。这些图片分两个时间段分别获取。本实验中,选取AR数据库中同一时间获取的100人(其中,男女各50人)不同表情、不同照度情况下的正面图像用于实验,每人选取7张图像。所有的人脸图像均被裁剪为120×160像素大小,选取12个特征点进行仿射变换对齐。部分对齐和归一化处理后的AR人脸图像如图1所示。

图1 部分AR人脸数据库样本图像
将对齐后的人脸图像,进行降质处理,得到与高分辨率图像对应的低分辨率人脸图像。降质过程如下

式中:X,y分别表示高、低分辨率人脸图像;B表示模糊核为8×8的平均模糊操作;U表示4倍下采样操作;n表示均方差为10的高斯加性噪声。在高、低分辨率人脸图像对中,随机选取90个人的630对人脸图像作为训练样本,剩下的10个人的70对人脸图像作为测试图像。图像分块的大小为8×8像素,相邻块交叠32像素。
为了验证算法的有效性,将本算法重建图像的主客观质量,与双三次插值算法、Jung提出的算法[9]进行比较。Jung方法中的正则化参数设置为0.05。本文提出方法中 λ =10,β =0.03,γ =0.05,K=5 。
图2为主观质量比较结果。从图中可以看出,双三次插值算法重建的结果非常平滑,但是不够清晰,也难以辨识。这主要是由于双三次插值算法在放大重建低分辨率图像过程中,并没有增加任何新的信息。Jung提出的方法都是基于块位置的人脸超分辨率方法,较之双三次插值方法,结果图像的清晰度有了明显的改进。但是,Jung提出的方法在重建图像的轮廓边缘都有明显的鬼影效应,重建人脸图像有或轻或重的眼镜假象。较之参考算法,本文提出的基于图约束稀疏编码的人脸超分辨率方法明显地改善了重建结果图像的清晰度,也减少了重建带来的人工效应和鬼影效果。本文方法取得了比参考算法更好的主观质量。

图2 主观质量
表1为客观质量比较结果。较之参照算法,本文提出的方法重建的结果图像在客观质量方面具有较高的峰值信噪比(PSNR)和结构相似性(SSIM)(PSNR和SSIM值均是越大越好),这表明本文方法重建的结果图像更接近于原始的高分辨率图像。

表1 客观质量比较结果
总之,无论从人眼视觉效果,还是客观评价指标,均表明本文提出的方法可以更好地对人脸图像进行超分辨率处理,获得更好的图像重建质量。
4 小结
本文提出了一种基于图约束字典和加权稀疏编码的人脸超分辨率算法。该算法在字典训练阶段引入图约束正则项,利用加权稀疏表示提高重建系数精确度,从而改进了已有算法性能。主客观仿真实验结果证明了该方法的有效性。后续研究中,自适应正则化参数的选择将有待进一步完善。
[1]BAKER S,KANADE T.Limits on super-resolution and how to break them[J].IEEE Trans.Pattern Analysis and Machine Intelligence,2002,24(9):1167-1183.
[2]WANG X,TANG X.Hallucinating face by eigentransform[J].IEEE Trans.Systems,Man and Cybernetics,2005,34(3):425-434.
[3]LIU C,SHUM H,ZHANG C.A two-step approach to hallucinating faces:global parametric model and local nonparametric model[C]//Proc.2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.[S.l.]:IEEE Press,2001:192-198.
[4]史云静,虞涛,朱秀昌.基于训练集分层的图像超分辨率重建[J].电视技术,2012,36(19):18-22.
[5]ZHANG Xuesong,PENG Silong,JIANG Jing.An adaptive learning method for face hallucination using locality preserving projections[C]//Proc.8th IEEE International Conference on Automatic Face&Gesture Recognition.[S.l.]:IEEE Press,2008:1-8.
[6]CHANG H,YEUNG D,XIONG Y.Super-resolution through neighbor embedding[C]//Proc.IEEE Computer Society Conference on Computer Vision and Pattern Recognition.[S.l.]:IEEE Press,2004:275-282.
[7]YANG J,TANG H,MA Y,et al.Face hallucination via sparse coding[C]//Proc.2008 IEEE International Conference on Image Processing.[S.l.]:IEEE Press,2008:1264-1267.
[8]CHANG L,ZHOU M.Face sketch synthesis via sparse representation[C]//Proc.2010 IEEE International Conference on Pattern Recognition.[S.l.]:IEEE Press,2010:2146-2149.
[9]JUNG C,JIAO L,LIU B,et al.Position-patch based face hallucination using convex optimization[J].IEEE Signal Processing Letters,2011,18(6):367-370.
[10]DONOHO D.Compressed sensing[J].IEEE Trans.Information Theory,2004,54(4):1289-1306.
[11]YANG S,WANG M,CHEN Y,et al.Single-image super-resolution reconstruction via learned geometric dictionaries and clustered sparse coding[J].IEEE Trans.Image Processing,2012,21(9):4016-4028.
[12]CAI D,BAO H,HE X.Sparse concept coding for visual analysis[C]//Proc.IEEE Computer Society Conference on Computer Vision and Pattern Recognition.[S.l.]:IEEE Press,2011:2905-2910.
[13]HE X,NIYOGI P.Locality preserving projections[C]//Proc.Advances in Neural Information Processing Systems 16(NIPS).[S.l.]:MIT Press,2003:290-307.
[14]BELKIN M,NIYOGI P.Laplacian eigenmaps and spectral techniques for embedding and clustering[C]//Proc.Advances in Neural Information Processing Systems.[S.l.]:MIT Press,2002:585-592.
[15]MARTINEZ A,BENAVENTE R.The AR face database[S].1998.

