Carrara大理岩高温高压变形实验研究*

宋茂双 邵同宾,2 李建峰 嵇少丞 王茜

1. 中国科学院广州地球化学研究所，同位素地球化学国家重点实验室，广州 5106402. 中国科学院大学，北京 1000493. 加拿大蒙特利尔综合工学院民用、地质与采矿工程系，蒙特利尔 H3C3A71.

1 引言

在地球演化历史过程中，海水通过有机沉积和无机沉积两种方式形成了大量的碳酸盐岩沉积物。即使在当今的海洋盆地、大陆架和滨海、浅海中碳酸盐岩的沉积作用仍比较活跃，并且这些地区分布有大量的碳酸盐岩礁石 (Oesterling, 2004)。因此，碳酸盐岩是固体地球上-中地壳的一种重要组成岩石。

由于碳酸盐岩沉积物为海相成因，处于板块的边缘地带，因此其常常参与造山作用。此外，它经常和俯冲板块一起被卷入增生楔且遭受变质和大量的变形作用。在中级变质条件下，碳酸盐岩沉积物就会转化为大理岩。细粒石灰岩的重结晶和生长亦可能形成粗粒大理岩。因此，方解石集合体在高温高压下的力学行为对于解释自然界的许多地质现象至关重要。例如，在剪切带和逆冲断层中，方解石岩层能够吸收大量的构造变形 (Bestmannetal., 2000; Burkard, 1993; Busch and van der Pluijm, 1995; Schmidetal., 1977)。大理岩作为一种典型的方解石岩石，其变形行为对我们理解地壳中的构造作用和造山事件具有重要的意义。

自岩石流变学实验开展以来 (如Von Kármán, 1911)，人们对方解石集合体进行了大量的研究(如Griggsetal., 1951; Turneretal., 1956; Heard, 1968; Rutter, 1972, 1974, 1995; Schmidetal., 1977, 1980; Wenketal., 1987; Fredrichetal., 1989; De Bresser, 1991; Paterson and Olgaard, 2000; Renneretal., 2002; De Bresseretal., 2005)，已经提出了三种主要的塑性流动机制 (Rutter, 1974; Schmidetal., 1977, 1980; Walkeretal., 1990)：1) 低温塑性或幂次律无效机制 (breakdown regime)；2) 中等温度下的蠕变机制，此时恢复、交叉滑移 (De Bresser and Spiers, 1993) 和边界滑移 (Walkeretal., 1990) 是非常重要的；3) 高温下的低应力机制，此时扩散蠕变和颗粒边界滑移占据主导地位 (Schmidetal., 1977, 1980; Walkeretal., 1990)。

本文利用中国科学院广州地球化学研究所2008年引进的高精度Paterson高温高压流变仪对Carrara大理岩在无水条件下进行了高温 (873～1173K) 高压 (～300MPa) 三轴压缩变形实验，实验应变速率约为10-6～10-3s-1，试样变形量最高达～27%。我们的实验结果表明，Carrara大理岩在873K和高应变速率时973K温度下主要是通过高应力机制变形，其本构关系服从指数定律；在1173～1073K和低应变速率时973K温度下主要通过位错蠕变机制发生变形，其本构关系服从幂次律。实验还发现，Carrara大理岩的蠕变强度随着温度的升高而降低，随着应变速率的增加先快速增加而后缓慢增加。对不同温度下应力指数的计算结果表明，随着温度的增加应力指数减小，表明应变速率对应力的敏感性随着温度的增加而减小。尽管在我们的实验条件下所有的应力指数都>5，但其变化趋势表明随着温度的增加，Carrara大理岩有可能在更高温度下发生扩散蠕变。

2 实验初始材料

本实验使用的初始材料——Carrara大理岩是产自阿尔卑斯山的一种绿片岩相变质大理岩，因其化学纯度高、显微结构均匀且CPO (Crystallographic preferred orientation) 各向同性而广受实验岩石流变学家的青睐。Carrara大理岩外表呈白色略带浅灰，没有发育面理。方解石颗粒没有初始的形状各向异性或晶体优选方位。镜下观察发现方解石颗粒边界平直，少数颗粒发育了双晶且双晶边界平直 (图1a)，没有观察到明显的前期变形特征。颗粒呈近等轴状。通过对图1a进行了368次线截距法测量，得到Carrara大理岩的粒度分布频率直方图 (图1b)。如图1b，我们得出大理岩的粒度分布呈现出轻微的负偏态，并且粒度主要集中在约80～200μm，其算术平均值为～146μm。此外，我们从照片中还可以看出大多数方解石颗粒边界常在三连点处呈～120度角度相交。

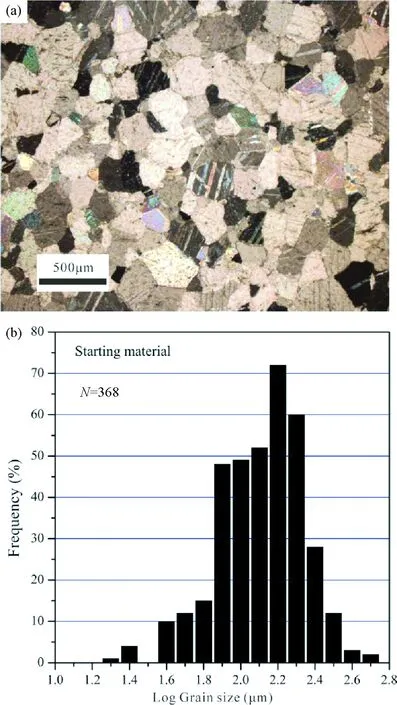
图1 初始材料Carrara大理岩的显微结构(a)-正交偏光显微照片；(b)-粒度分布的频率直方图Fig.1 Microstructures of starting material Carrara marble(a)-cross-polarized light micrograph; (b)-frequency histogram of grain size distribution

3 实验细节

Carrara大理岩在高温高压下的变形实验是在Paterson高温高压流变仪(邵同宾等, 2011)上完成的。首先利用金刚石空心钻从一块Carrara大理岩岩块上钻取直径为～10mm长度为～20mm的圆柱样品若干，通过对圆柱两底面进行抛光处理使得两底面平行度在10μm以内。将钻好的样品放入蒸馏水中超声清洗～15min，然后放在烘箱中在120℃温度下干燥至少24h，于实验使用时取出。为了进行力学测试，试样被置于壁厚为～0.25mm的铁筒中并且两端使用无孔垫片将试样与活塞隔开(图2)。开展变形实验之前通过虚拟样品与有孔活塞相连在不同的实验温度和压力条件下对样品集中间50cm长度区间上的温度进行标定，标定结果表明在样品组装中部50cm的长度区间温度变化可以控制在小于5K，在样品分布区域即2cm长度范围内温度变化不超过±2K。仪器应力传感器内置，且利用氩气作为围压介质，因而应力测量精度高 (±0.1MPa)。实验开始时，先气动增压升至～75MPa，然后通过油压机进行一至二次加压至一定压力 (<目标压力，与目标压力之间的差值一般根据实验的目标温度来设定，大约每升高8K围压上升1MPa)，接着按30K/min的速率升温至目标温度，此时围压也达到目标压力。等温度平衡 (需～5min) 后，根据实验设计要求进行不同应变速率下的变形实验。变形实验结束后，关闭加热系统使样品快速淬冷，待温度降至～400K时手动缓慢卸压至室压。待炉子内温度回到室温后取出样品进行后期处理与分析。

图2 Carrara大理岩三轴变形实验样品组装示意图Fig.2 Schematic illustration of sample assembly in the triaxial deformation experiments for Carrara marble

4 力学结果

利用Paterson高温高压流变仪对Carrara大理岩在300MPa围压下进行了三轴压缩变形实验 (σ1>σ2=σ3>0)。变形温度为873～1173K，轴向应变速率为约10-6～10-3s-1。在该实验条件下，大理岩的流动强度对应于差应力的大小 (σ=σ1-σ3)，即为最大压缩应力 (σ1) 与最小压缩应力 (σ3) 之间的差值。因此，它总是一个正值。根据仪器采集系统记录的加载应力和位移数据，然后通过校正铁筒强度、仪器变形量和样品横截面面积与长度的变化 (校正方法详见邵同宾, 2012；李建峰等, 2013)，可以获得试样的真实差应力和轴向应变量(表1)。

表1所示12个Carrara大理岩圆柱样品轴向变形实验的条件和力学结果。表中列出的试样的强度一般是在应变量>4%读取的，对于逐级应变速率实验有些试样的强度是在应变量≤3.5%读取的，所读取的强度可能是非稳定态的。最大累积应变量达27%。试样CM012的变形温度由于热电偶故障而未能准确监测，但仍可用于分析应变速率对Carrara大理岩流动行为的影响。

4.1 应力-应变曲线

图3所示为Carrara大理岩在300MPa围压、873～1173K温度、应变速率为10-5～2.65×10-4s-1条件下轴向压缩变形的应力-应变曲线。应力-应变曲线的形状显示随着应变量增大，差应力起初快速增加，随后是缓慢的应变硬化；在高温 (如1073K和1173K) 下应变超过～12%时，应力-应变曲线表现出微弱的应变软化；而在873K温度下，即便是应变量高达10%，应力-应变曲线仍呈较明显的应变硬化趋势。轴向应变为10%、2%、6%、7%、16%和17%时，Carrara大理岩的流动强度分别为162.88MPa、77.5MPa、74.7MPa、69.6MPa、63.7MPa和37.2MPa (表1)，其中在2%的应变量时，Carrara大理岩的应变硬化较为明显。CM009试样由于变形温度低，达到稳定态所需的应变量比相同应变速率较高温度的实验所需的应变量要大。其他试样 (如CM002、CM001、CM011和CM010) 的应力-应变曲线在应变量>4%时较为平直，指示已达到较好的稳态流变。

表1 Carrara大理岩三轴压缩变形实验条件及力学结果

Table 1 Experimental conditions and mechanical results of triaxial deformation experiments for Carrara marble

样品号温度(K)压力(MPa)应变速率(s-1)强度(MPa)应变量(%)CM0098733001．13×10-4162．8810CM0148733001．13×10-5134．54CM0148733001．13×10-4165．610CM0148733001．11×10-3191．915．2CM0069733006．26×10-661．191CM0069733008．33×10-679．82CM0069733003．16×10-589．74．5CM0069733005．19×10-596．57CM0069733001．11×10-4106．412CM0069733002．77×10-595．115CM0069733002．90×10-4118．520CM0069733001．06×10-3131．825CM0079733001．04×10-577．52CM0089733009．57×10-683．31．5CM0089733001．11×10-4106．74CM00210303009．20×10-574．76CM00110603002．65×10-469．67CM00810733001．03×10-546．41CM00810733008．64×10-576．74CM00810733005．32×10-482．78CM01110733001．14×10-463．716CM012？3001．02×10-5354．9CM012？3009．51×10-547．612．2CM012？3008．99×10-463．817CM00411733102．38×10-527．32CM00411733106．54×10-535．63．5CM00411733101．11×10-438．66CM00811733109．52×10-625．21．2CM00811733101．09×10-443．54CM00811733105．03×10-452．911CM00811733101．05×10-35715CM01011733001．08×10-437．217CM01311733001．10×10-524．64CM01311733001．12×10-438．29CM01311733007．42×10-453．820

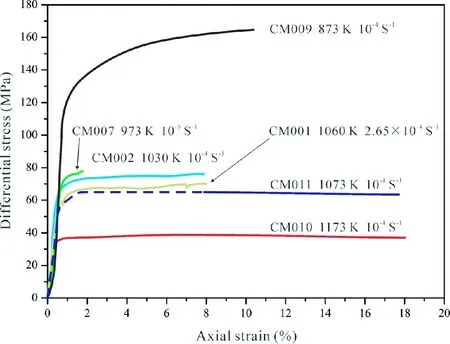
图3 Carrara大理岩在300MPa围压不同应变速率下的应力-应变曲线 Fig.3 Stress-strain curves of Carrara marble at different strain rates under a confining pressure of 300MPa

图4 Carrara大理岩在300MPa围压条件下逐级应变速率实验获得的应力-应变曲线Fig.4 Stress-strain curves of Carrara marble deformed by step strain rates at a confining pressure of 300MPa

此外，需要说明的是，试样CM011在变形过程中数据采集用的电脑系统出现临时故障导致数据记录不完整 (在图中表现为实线部分)，因而在达到稳定态变形的情况下，我们用虚线表示试样CM011应力-应变曲线的前段部分。基于图3所示，我们比较容易得出在相同围压和应变速率下，试样的强度随着温度的升高而降低。例如，比较CM009和 CM011 与CM011和CM010，我们可以发现在300MPa围压和10-4s-1应变速率下，从873K到1073K再到1173K，Carrara大理岩的强度分别减小60.9%和41.6%。

为了研究应变速率对Carrara大理岩轴向变形行为的影响，我们在300MPa围压和每个温度下对试样进行了逐级应变速率(也称梯级：step strain rate)实验，累积应变量最低达～5%，最高可达～27% (图4)。由于逐级实验需要不同的应变速率来实现，因此我们进行的应变速率逐级实验至少包括2次不同的应变速率加载(如CM008, 973K)，最多的包括8次(如CM006)，每次加载的应变速率大小详见表1。对Carrara大理岩应变速率逐级变形的应力-应变曲线观察发现，在相同温度下试样的强度随着应变速率的增加而增大 (如CM014、CM008、CM012、CM013和CM004)，随着应变速率的减小而减小(如CM006)。此外，我们还发现，随着应变速率的增加，试样达到稳定态所需的应变量增加，也即图中所示应力-应变曲线上屈服点随着应变速率的增加而延迟或滞后。观察试样CM012的应力-应变曲线，我们发现在应变量高达～20%时出现了较显著的应变软化。

4.2 流动律参数

方解石岩石的变形机制与应力、应变速率和粒度有关，其在高温和低应变速率下的变形主要由扩散蠕变或位错蠕变控制，其中前者涉及点缺陷运动而后者涉及位错迁移(如Schmidetal., 1980; Rutteretal., 1994)。扩散和位错蠕变机制中的应变速率常常可由下列本构方程来表述：

(1)

这里的A是指前因子，σ是差应力，Q是活化能，R是气体常数，T是绝对温度，n是应力指数，m是指示应变速率对粒度敏感性的常数，也可称粒度指数。由扩散蠕变控制的线粘性蠕变模型要求n=1且m=2 (Nabarro-Herring蠕变) 或者m=3 (Coble蠕变) (Ji and Xia, 2002)。为了简便起见，在不强调变形是由扩散和颗粒边界滑移控制时我们将这种变形统称为扩散蠕变 (Schmidetal., 1977)。

尽管一些学者已经质疑是否可将公式 (1)应用于方解石岩石的位错蠕变变形(Covey-Crump, 1998; Renner and Evans, 2002)，因为当利用公式(1)时计算的n值通常在3和9之间 (Schmidetal., 1980; Brodie and Rutter, 2000; De Bresseretal., 2002)。但是，以温度和应力构建的变形机制域的两个端元机制分别为扩散蠕变和位错蠕变 (Rutter, 1995)。在这两个机制的过渡区，两个机制都起作用且n在2和5之间。有趣的是，将方解石的本构方程外延至自然条件表明在中级变质条件下，如果粒度小于1mm那么方解石岩石的主导变形机制是粒度敏感的扩散蠕变。

需要说明的是，考虑到前人在与本实验相当的条件下并没有观察到Carrara大理岩发生扩散蠕变，因此粒度的影响不大，所以我们假定实验过程中粒度不变，那么公式 (1) 可改写为：

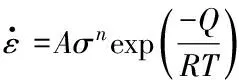
(2)

为了求应力指数n和活化能Q，我们对上式取自然对数得到

(3)

(4)

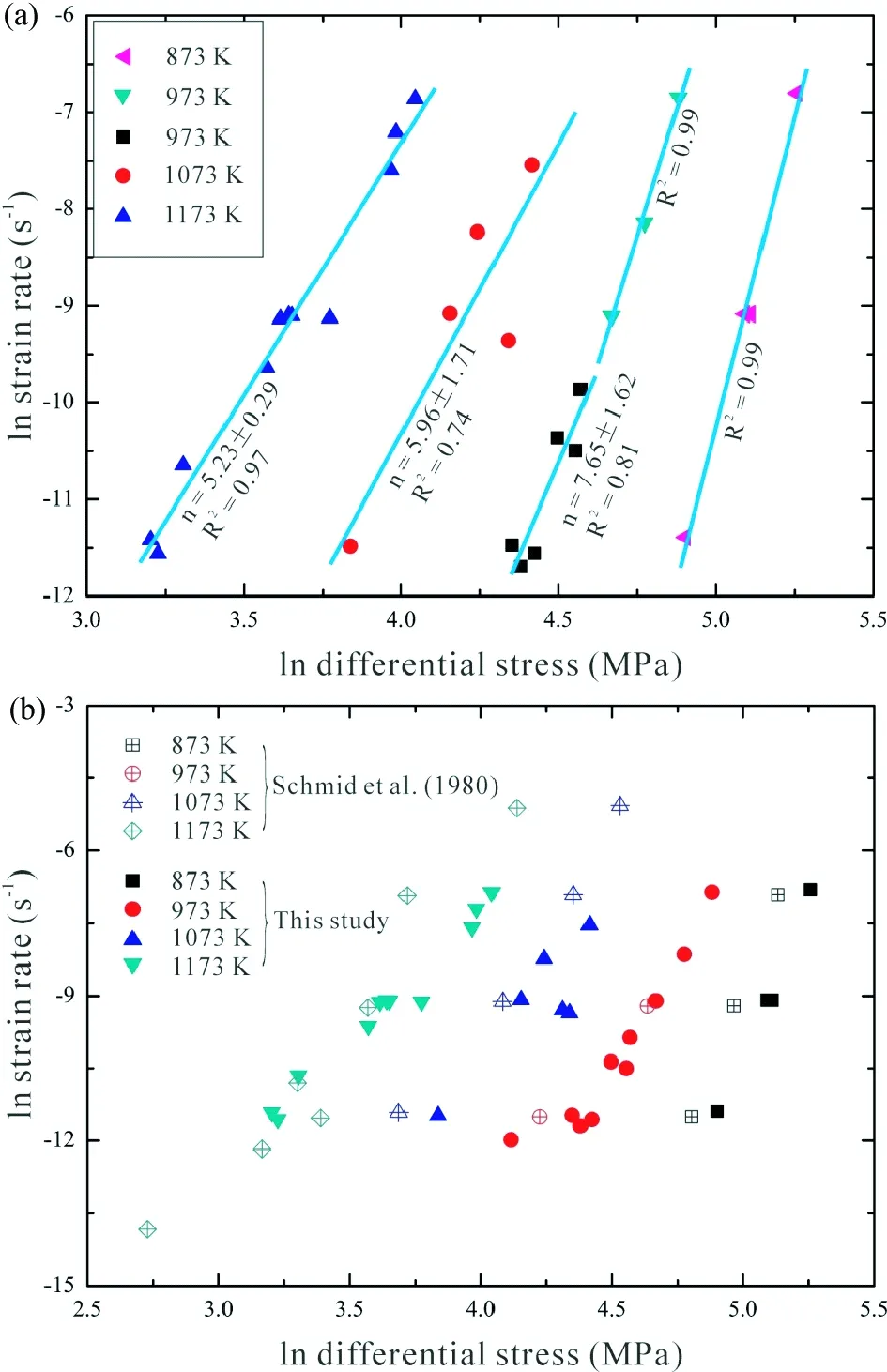
图5 Carrara大理岩在300MPa围压和873～1173K温度下差应力-应变速率双对数投图(a)-本研究获得的实验结果；(b)-本研究与Schmid et al. (1980)实验数据的对比Fig.5 Log-log plot of differential stress vs. strain rate of Carrara marble deformed at a confining pressure of 300MPa and temperatures ranging from 873K to 1173K(a)-experimental data in this study; (b)-a comparison of data between us and Schmid et al. (1980)

利用公式(3)，我们对不同温度下的差应力和应变速率进行了双对数投图，并进行了线性拟合 (图5a)。由于实验的局限性，所以还不能完全避免应力指数n随着温度的变化而变化 (Herweghetal., 2003)。随着温度的升高大理岩变形的主导机制会发生逐渐的改变，因此尽管在同一个变形机制域 (如位错蠕变)，但n值却变化较大。根图5a，我们发现随着温度的升高拟合直线的斜率逐渐减小，尤其是温度从873K升高到1073K时，这其中Carrara大理岩很可能存在不同的变形机制。在1073K到1173K时，斜率减小仅6.3%，因此在这两个温度条件下，大理岩应在同一机制域变形。总体来说，根据图5a我们不可能得出一个单一的经验流动律来满足所有的数据点，这与Schmidetal. (1980) 在对873～1323K温度下数据点的分析是类似的。在他们的分析中，根据应力的大小，他们将Carrara大理岩的变形机制划分为以下三类。

机制1用指数定律表示，要求σ>100MPa，适用于773K、873K以及973K的温度条件，由于要满足σ>100MPa，因此还要求973K温度下的变形速率要快。这一本构律率先由Rutter (1974) 建立，后被Schmidetal. (1980) 完全吸收并引用，指数关系为：

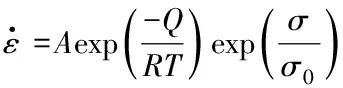
(5)

其中A=5.9×105s-1，σ0=11.4MPa，活化能Q=259.2kJ/mol。

表2指数律本构关系的验证

Table 2 Vertifation for the exponential relationship using the data from Schmidetal. (1980) and this study

样品号T(K)ε·(s-1)σ(MPa)①lnε·②Q/RT③lnA④σ/σ0⑤=①+②-③∗(④-⑤)/④CM009873113×10-416288-908812335706206132878778214287719313330205540067016557CM014873113×10-51345-1139071357062061328787782117982456111027620450065316929CM014873113×10-41656-9088123357062061328787782145263157913330205540082340923CM014873111×10-31919-6803395357062061328787782168333333315614933020072380217CM006973111×10-41064-91059832036504132878778293333333339642645344-0033140573CM006973290×10-41185-81456332036504132878778210394736841060299607-0020035065CM006973106×10-31318-684948632036504132878778211561403511189913933-0029212355CM008973111×10-41067-91059832036504132878778293596491239642645344-00302357724128873100×10-31695-6907755357062061328787782148684210515510573-00431889812743R873100×10-41435-9210343570620613287877821258771931320798791-00492756942742873100×10-51219-115129335706206132878778210692982461090540281-00198653992751R973100×10-41148-9210343203650413287877821007017544953828532900528183562758R973100×10-41031-92103432036504132878778290438596499538285329-0054669765

注：*表示将数据代入公式(5)得出的误差

机制2用幂次律表示，要求20<σ<100MPa，主要适用于1073～1173K温度下的实验数据但也可延伸至低应变速率下的低温 (如973K) 和高应变速率时的高温 (如1273K) 情况。这一本构关系与上述公式(1)完全相同。他们根据实验数据拟合计算得到的流动律参数为：logA=-4.5±0.4s/MPa，Q=418±42kJ/mol，n=7.6±0.8。

机制3，要求σ<20MPa。他们利用幂次律公式对强度在20MPa以下的数据进行了拟合，通过计算得出流动律参数为：logA=-3.9±0.2s/MPa，Q=426±46kJ/mol，n=4.2±0.4。

比较我们在表1中所示的实验数据和上述Schmidetal. (1980) 提出的三种机制，我们认为本研究的实验数据主要落在机制1和机制2的范围内。下面我们通过实验数据的代入和拟合计算来验证这一推测。

将Schmidetal. (1980) 的实验数据 (4128、2743R、2742、2751R和2758R) 和本研究中强度>100MPa的数据进行综合集成并代入公式(5)计算得到表2。从表2中我们可以看出，我们的数据误差为～(2.5±5.5)%，Schmidetal. (1980) 的数据误差为～±5%。因此，我们认为本研究中873K和变形速率较快时973K下Carrara大理岩的变形机制服从上述指数律本构关系。

通过应变速率对差应力的双对数投图，我们发现在973K温度下高应变速率和低应变速率的数据拟合线斜率发生了较大的转变 (从10.47减小为7.65)，而在873K温度下拟合线斜率为12.78，这与Schmidetal. (1980) 的拟合线斜率变化是类似的。尤其是，我们在973K时的拟合线斜率 (即应力指数n) 与Schmidetal. (1980) 机制2幂次律本构方程中的应力指数 (n=7.6) 非常接近。此外，我们在较高温度 (1073K和1173K) 下数据点的拟合线斜率分别为5.96和5.23，在这些温度下Carrara大理岩的变形与Schmidetal. (1980) 中的一样，也是由幂次律蠕变控制的。基于以上分析，我们虽然在机制2中没有得出一个统一的应力指数n值，但我们能够比较确切地得出本研究中Carrara大理岩的变形机制与Schmidetal. (1980) 的前两种机制是一致的。

对在1173K 、1073K和低变形速率时973K温度下实验数据拟合得到的应力指数n，取平均得到n=6.44±1.21。结合公式 (4)，我们对应变速率为～10-5s-1条件下流变强度和温度的倒数进行投图得到图6。根据图6a所示方程，我们计算得到活化能Q=348±40kJ/mol，lnA=3.3±0.7。与此同时，为了说明我们的数据与Schmidetal. (1980) 实验数据之间的差异，我们分别在图5b和图6b进行了投图。比较发现，总体来说Schmidetal. (1980) 的数据比我们的稍低，个别数据比我们的略高，这与De Bresseretal. (2005) 得出的结论基本一致。

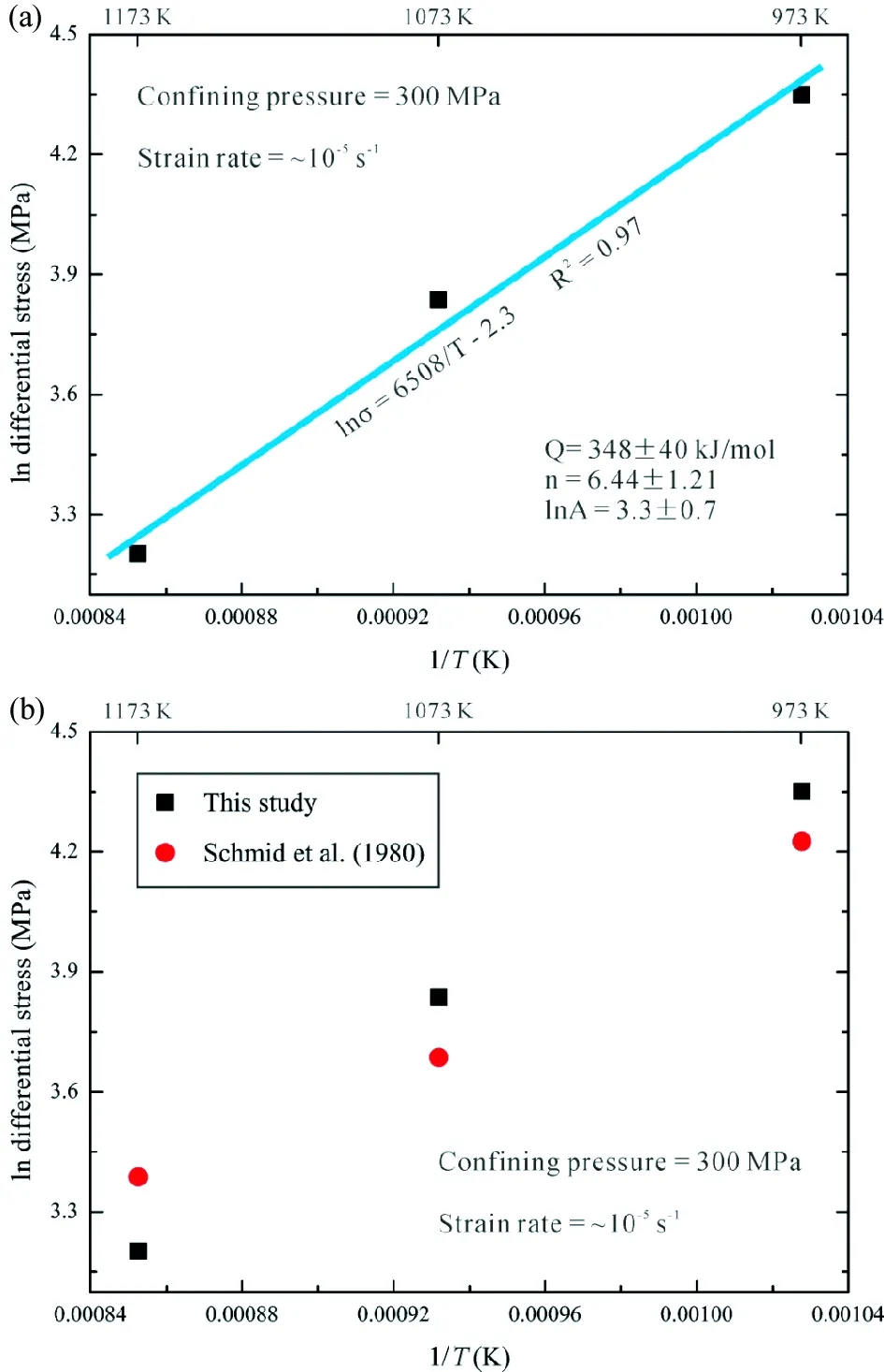
图6 Carrara大理岩变形实验的力学结果(a)-差应力在～1×10-5s-1应变速率下对温度倒数的投图; (b)-本研究和Schmid et al. (1980) 在～1×10-5s-1应变速率下差应力与温度倒数的的数据Fig.6 Mechanical results of deformation experiments on Carrara marble(a)-differential stress at strain rate ～1×10-5s-1 plotted against reciprocal temperature. Best fit line is based on linear regression in lnσ-1/T space; (b)-differential stress-reciprocal temperature at strain rate ～1×10-5s-1 from the present study and Schmid et al. (1980)

5 结论与讨论

在300MPa围压、873～1173K温度以及约10-6～10-3s-1应变速率下，我们对Carrara大理岩进行了一系列等应变速率单一和逐级应变速率实验。Carrara大理岩作为一种低强度的地壳岩石，其力学行为受温度和应变速率的影响要比受压力的影响大得多。在其他条件相同时，温度的增加会促进Carrara大理岩的变形，使得其稳定态强度和达到该强度所需的应变量均减小；而应变速率的增加会使得试样的稳定态蠕变滞后，也即达到稳定态所需的应变量会增大，相应的稳定态强度也会增大。应变量的大小对应力-应变曲线的形状具有显著的影响。在应变量<～2%时，Carrara大理岩在在低温或高应变速率下的应力-应变曲线仍表现出较明显的应变硬化。而在应变量高达～20%时，Carrara大理岩呈现出较明显的应变软化行为，这很可能是由高温下颗粒发生动态重结晶所致。

基于流动律参数的计算结果，我们还得出在873K和高应变速率时973K温度下Carrara大理岩的变形机制与Rutter (1974) 和Schmidetal. (1980) 研究中的机制1相一致，且具有参数相同的指数律本构方程。在高温和低应变速率低温 (973K) 下，虽然Carrara大理岩的应力指数随着温度的升高而减小(尤其是在973K和1073K温度下更为明显)，但都属于位错蠕变变形 (Schmidetal., 1980; Brodie and Rutter, 2000; De Bresseretal., 2002)，服从幂次律本构关系，与Schmidetal. (1980) 中的机制2相一致。由于本研究中试样的变形温度最高为1173K，其变形强度均>20MPa，因此这里的Carrara大理岩变形没有出现Schmidetal. (1980) 建立的变形机制3。通过比较，我们发现本研究中Carrara大理岩的流动强度总体上要比Schmidetal. (1980) 的略高一些。虽然我们的试样平均粒度(～150μm)要比他们的(～200μm)小，但由于在我们与Schmidetal. (1980) 的实验中Carrara大理岩的变形机制均不在扩散蠕变域，因此我们认为这种强度差异受粒度的影响不是很大。

致谢感谢瑞士联邦理工学院 (ETH) HPT岩石变形实验室的Luigi Burlini博士提供实验样品；感谢周永胜老师对本文提出的有益建议。

Bestmann M, Kunze K and Matthews A. 2000. Evolution of a calcite marble shear zone complex on Thassos Island, Greece: Microstructural and textural fabrics and their kinematic significance. Journal of Structural Geology, 22(11-12): 1789-1807

Brodie KH and Rutter EH. 2000. Deformation mechanisms and rheology: Why marble is weaker than quartzite. Journal of the Geological Society, London, 157(6): 1093-1096

Burkard M. 1993. Calcite twins, their geometry, appearance and significance as stress-strain markers and indicators of tectonic regime: A review. Journal of Structural Geology, 15(3-5): 351-368

Busch JP and Van der Pluijm BA. 1995. Calcite textures, microstructures and rheological properties of marble mylonites in the Bancroft shear zone, Ontario, Canada. Journal of Structural Geology, 17(5): 667-688

Covey-Crump SJ. 1998. Evolution of mechanical state in Carrara marble during deformation at 400℃ to 700℃. Journal of Geophysical Research, 103(B12): 29781-29794

De Bresser JHP. 1991. Intracrystalline deformation of calcite. Ph. D. Dissertation. Dutch: University of Utrecht

De Bresser JHP and Spiers CJ. 1993. Slip systems in calcite single crystals deformed at 300～800 degrees C. Journal of Geophysical Research, 98(B4): 6397-6409

De Bresser JHP, Evans B and Renner J. 2002. On estimating the strength of calcite rocks under natural conditions. In: De Meer S, Drury M, de Bresser JHP and Pennock GM (eds.). Deformation Mechanisms, Rheology and Tectonics. Geological Society, London, Special Publications, 200(1): 309-329

De Bresser JHP, Urai JL and Olgaard DL. 2005. Effect of water on the strength and microstructure of Carrara marble axially compressed at high temperature. Journal of Structural Geology, 27(2): 265-281

Fredrich JT, Evans B and Wong TF. 1989. Micromechanics of the brittle to plastic transition in Carrara marble. Journal of Geophysical Research, 94(B4): 4129-4145

Griggs DT, Turner FJ, Borg I and Sosoka J. 1951. Deformation of Yule marble, Part Ⅳ. Geological Society of America Bulletin, 62(12): 1385-1406

Heard HC. 1968. Steady-state flow in Yule marble at 500～800 degrees C. Transactions-American Geophysical Union, 59(1): 312

Herwegh M, Xiao XH and Evans B. 2003. The effect of dissolved magnesium on diffusion creep in calcite. Earth and Planetary Science Letters, 212(3-4): 457-470

Ji SC and Xia B. 2002. Rheology of Polyphase Earth Materials. Polytechnic International Press, 1-259

Li JF, Song MS, Shao TB and Wang Q. 2013. Calibration methods for the axial deformation data recorded by Paterson rig. Geotectonica et Metallogenia, 37(1):127-137 (in Chinese with English abstract)

Oesterling N. 2004. Dynamic recrystallization and deformation mechanisms of naturally deformed Carrara marble: A study on one- and two-phase carbonate rocks. Ph. D. Dissertation. Switzerland: Basel University, 1-292

Paterson MS and Olgaard DL. 2000. Rock deformation tests to large shear strains in torsion. Journal of Structural Geology, 22(9): 1341-1358

Renner J and Evans B. 2002. Do calcite rocks obey the power-law creep equation? In: De Meer S, Drury M, de Bresser JHP and Pennock GM (eds.). Deformation Mechanisms, Rheology and Tectonics. Geological Society, London, Special Publications, 200(1): 293-307

Renner J, Evans B and Siddiqi G. 2002. Dislocation creep of calcite. Journal of Geophysical Research, 107(B12), ECV 6-1-ECV 6-16, doi:10.1029/2001JB001680

Rutter EH. 1972. The influence of interstitial water on the rheological behaviour of calcite rocks. Tectonophysics, 14(1): 13-33

Rutter EH. 1974. The influence of temperature, strain rate and interstitial water in the experimental deformation of calcite rocks. Tectonophysics, 22(3-4): 311-334

Rutter EH, Casey M and Burlini L. 1994. Preferred crystallographic orientation development during the plastic and superplastic flow of calcite rocks. Journal of Structural Geology, 16(10): 1431-1446

Rutter EH. 1995. Experimental study of the influence of stress, temperature, and strain on the dynamic recrystallization of Carrara marble. Journal of Geophysical Research, 100(B12): 24651-24663

Schmid SM, Boland JN and Paterson MS. 1977. Superplastic flow in fine grained limestone. Tectonophysics, 43(3-4): 257-291

Schmid SM, Paterson MS and Boland JN. 1980. High temperature flow and dynamic recrystallization in Carrara Marble. Tectonphysics, 65(3-4): 245-280

Shao TB, Ji SC, Li JF, Wang Q and Song MS. 2011. Paterson gas-medium high-pressure high-temperature testing system and its applications in rheology of rocks. Geotectonica et Metallogenia, 35(3): 457-476 (in Chinese with English abstract)

Shao TB. 2012. Experimental method of triaxial compression deformation in a Paterson gas-medium high-pressure high-temperature testing system and its applications in rheology of rocks. Master Degree Thesis. Beijing: Graduate University of Chinese Academy of Sciences, 1-114 (in Chinese with English abstract)

Turner FJ, Griggs DT, Clark RH and Dixon RH. 1956. Deformation of Yule marble, Part Ⅶ. Geological Society of America Bulletin, 67(9): 1259-1294

von Kármán T. 1911. Festigkeitsversuche unter allseitigem Druck. Zeitschrift des Vereins deutscher Ingeniure, 42(55): 1749-1758

Walker AN, Rutter EH and Brodie KH. 1990. Experimental study of grain-size sensitive flow of synthetic, hot-pressed calcite rocks. In: Knipe RJ and Agar SM (eds.). Deformation Mechanisms, Rheology and Tectonics. UK: Geological Society, 259-284

Wenk HR, Takeshita T, Bechler E, Erskine BG and Matthies S. 1987. Pure shear and simple shear calcite textures: Comparsion of experimental, theoretical and natural data. Journal of Structural Geology, 9(5-6): 731-745

附中文参考文献

李建峰, 宋茂双, 邵同宾, 夏莹, 王茜, 周微. 2013. Paterson高温高压流变仪轴向变形实验数据校正方法. 大地构造与成矿学, 37(1):127-137

邵同宾, 嵇少丞, 李建峰, 王茜, 宋茂双. 2011. Paterson高温高压流变仪及其在岩石流变学的应用. 大地构造与成矿学, 35(3): 457-476

邵同宾. 2012. Paterson高温高压流变仪三轴压缩变形实验方法及其在岩石流变学中的应用. 硕士学位论文. 北京: 中国科学院研究生院, 1-114