改进的K-Means算法在特征关联中的应用∗

关 欣,孙祥威,曹昕莹

(海军航空工程学院信息融合技术研究所,山东烟台264001)

0 引言

随着现代科学技术在军事领域的广泛应用,现代战争已经突破了传统模式,发展成为陆、海、空、天、电磁五位一体的战争。在现代战术系统中,依靠单一传感器系统提供信息已无法满足作战需要,必须运用多个传感器系统来提供观测信息,这就需要对多传感器系统获取的信息进行综合处理,实时进行目标发现和优化综合处理来获取目标状态估计、目标属性及目标身份、态势评估、威胁估计等作战信息[1-3]。

特征关联是无源多传感器辐射源融合识别的一个关键环节。无源多传感器融合识别系统需要直接融合来自同类信源的数据,然后进行特征提取和利用融合数据进行属性判决。为了使这种融合顺利进行,首先需要利用同类信源获取的辐射源特征信息特征进行特征关联,保证被融合的数据对应于相同的辐射源。

特征关联产生于传感器量测过程中的不确定性。理论上,源自同一辐射源的量测数据中的特征值是相同的,但由于传感器存在测量误差,且不同的辐射源之间本身也可能存在特征上的相似性,这些都使量测值与其源自的辐射源之间的对应关系出现了模糊性。特征关联是将无源多传感器获取的多个辐射源的特征参数相关为一组,而每一组表示与一个单一可分辨的辐射源有关的数据,确定每组观测属于哪个已知辐射源的观测或是潜在辐射源的新的观测,从而消除关联模糊,它的本质是分类问题。

对于分类算法选取问题,文献[4]针对未知的雷达辐射源信号,提出了一种新的基于数据势场聚类的未知雷达信号分选方法,解决了分类数确定的问题;文献[5]利用改进的K-Means算法解决了参数相近、互相交叠的非常规雷达信号的分类问题。但这些分类算法都面临着分类数确定和分类效果评估的问题。本文改进了K-Means算法,并将其应用到特征关联上,解决了雷达辐射源数量估计和分类效果评估的问题。

1 特征关联过程

图1给出了特征关联的具体过程:首先是利用雷达辐射源特征矢量,由预先定义的相似性度量计算相似度得到相似矩阵,进而确定特征矢量组中哪些是对同一雷达辐射源的描述,即确定多量测之间能否归到一起,以表示它们是相同的潜在实体的分离观测。这种分类结果是否合理,需要进行检验,如果不合理则重复分类直到输出合理的检验结果。

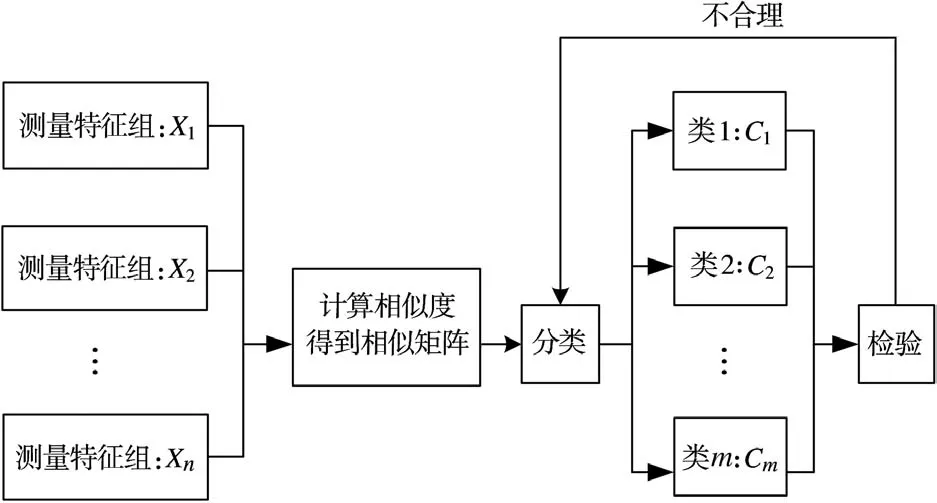
图1 特征关联过程图

2 改进的K-Means算法

2.1 K-Means算法

K-Means算法是Mac Queen提出的一种非监督实时聚类算法,在最小化误差函数的基础上将数据划分为预定的簇数k。设待分类的样本集为X={x1,x2,…,x n},分类数目k(k≤n)是事先确定的,该方法取定k类和选取k个初始聚类中心,按最小距离原则将各样本分配到k类中的某一类,之后不断地计算类心和调整各样本的类别,最终使各样本到其所属类别中心的距离平方之和最小[6]。

具体运算步骤如下:

(1)任选k个样本作为初始聚类中心:z(0)1,

(2)将待分类的样本集X中的样本逐个按最小距离原则分划给k类中的某一类,即若

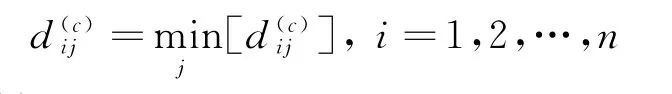
则判

(3)计算重新分类后的各类心

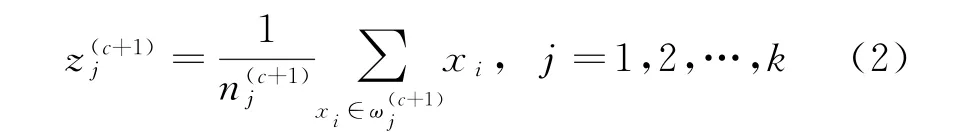
在上述步骤中,虽然没有直接运用准则函数

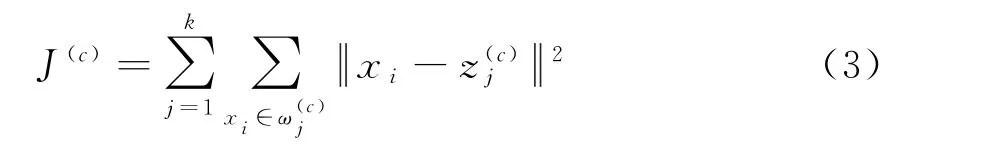
进行分类,但在步骤(2)中根据式(2)进行划分可使J(c)趋于变小。

K-Means算法的时间复杂度是O(m×n×k×t),空间复杂度是O((n+k)×m)。其中n表示所有样本点的个数,k是类数目,t是迭代次数,m是样本的属性个数,通常k≪n且t≪n。影响K-Means算法性能的因素主要有两个:①聚类数k的选取;②初始聚类中心的选取。针对初始聚类中心选取问题,文献[7]通过区域划分方法估算出k个中心点作为初始聚类中心,减少了迭代次数,提高了算法质量;文献[8]采取对数据进行预处理的方式选取初始中心,提高了算法效率。

2.2 聚类数k的确定

在聚类数未知的情况下使用K-Means算法,可让聚类数k从较小值逐步增加,在这个过程中,对于每个选定的k分别使用该算法。显然,准则函数J是随着k的增加而单调减少,如果作一条J-c曲线,其曲率变化的最大点对应的类数是比较接近从几何分布上看最优的类数。由于从J-c曲线上观察曲率变化的最大点不直观,本文使用聚类有效性指标S来确定最佳聚类数

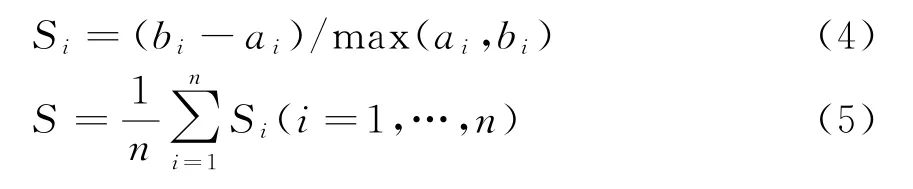
式中,a i表示第i个样本到其所在类中其他样本的平均距离;b i表示第i个样本到其他类中样本的最小平均距离。对于不同的k值时,S值不同,S值最大时对应的k值为最佳聚类数。

2.3 灰关联度

灰色系统理论是由邓聚龙教授于1982年创立的,是一种研究少数据、贫信息不确定性问题的新方法。灰关联分析根据数据列因素之间发展态势的相似或相异程度来衡量因素间接近的程度,由于关联分析是按发展趋势作分析,对样本集的大小没有太高的要求,分析时也不需要典型的分布规律,而且分析的结果一般与定性分析相吻合。可用于每类雷达有多个模式以及侦测参数不全的场合,适应部分雷达辐射源侦察信号“少数据”、“贫信息”的特点[9]。

计算样本间的灰关联度,一般包括下列的计算和分析步骤。

(1)确定参考序列和比较序列

选取样本集中的一个样本作为参考序列,记为x i={x i(k)|i=1,2,…,n},选取样本集中其余的样本作为比较序列,记为x j≠i={x j(k)|j=1,2,…,n},其中k为样本维数,n为样本集合中样本总数。

(2)对样本进行标准化处理

在对样本进行处理时,量纲选取不同会改变某特征的判断依据性,即改变该特征对判断贡献的大小,严重的可造成错误分类。因此,首先需要对样本集进行标准化处理,本文用区间值变换法对样本集进行标准化处理。

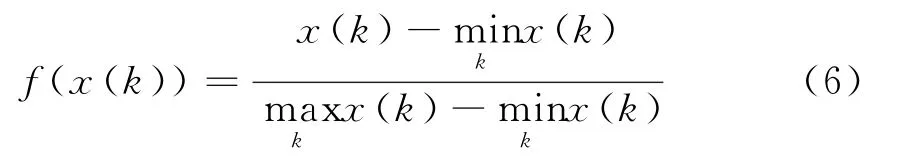
(3)求关联系数

参考序列x i(k)和比较序列x j(k)的关联系数定义如下:

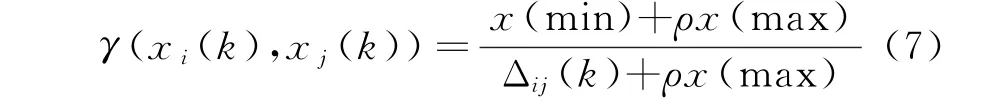
式中,Δij(k)=|x i(k)-x j(k)|为绝对差;为两级最小差;为两级最大差;ρ为分辨系数,且ρ∈(0,1),一般取ρ=0.5;上述定义的γ(x i(k),x j(k))称为k点的灰色关联系数。

(4)计算灰关联度

将每一比较序列各个特征的关联系数集中体现在一个值上以便于比较,这个值就是灰关联度,常用的计算灰关联度的方法是平均值法,即

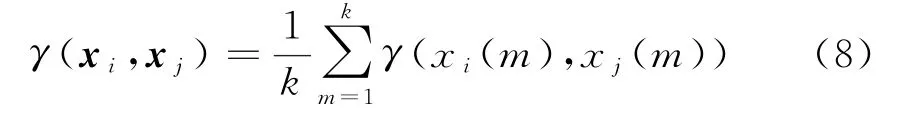
2.4 改进的K-Means算法流程图

图2给出了改进的K-Means算法计算流程图,K-Means算法中定义样本之间距离d ij()的方法有绝对值距离、欧氏距离、切比雪夫距离、马氏距离,改进的K-Means算法使用灰关联度定义样本间的距离。改进的K-Means算法的时间复杂度是O(m×n2×k×t),空间复杂度是O((n2+k)×m)。计算时设置分类数从2开始逐步增大,在平方误差和准则E收敛时,输出聚类结果,计算聚类结果的聚类有效性指标,取有效性指标值最大时对应的k值为最佳聚类数 。

平方误差和准则定义如下:

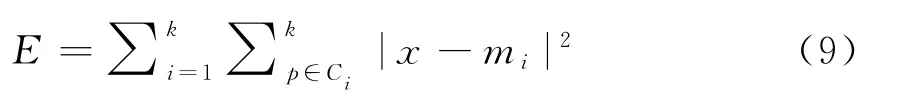
E是数据库中所有对象的平方误差总和,x是空间中的样本点,表示给定的数据对象,m i是类C i的平均值,这个准则使生成的结果类尽可能地紧凑和独立。

3 计算机仿真及结果分析

3.1 模拟产生雷达辐射源特征信息

实验中仿真模拟2部雷达侦察设备对同方向的3部复杂体制雷达辐射源信号侦察与截获,考虑到真实环境下存在的各种噪声和各个侦察设备的测量误差,设定脉冲重复频率误差为5 Hz,载频误差为5 MHz,脉宽误差为0.2μs,样本点数值大小见表1。假设共获取了300组特征矢量作为样本构成样本集,称该样本集为Radar-database,样本集含有300个样本,形成3类,并且类之间有轻微重叠,每个样本有3个特征,每类中各有100个样本。

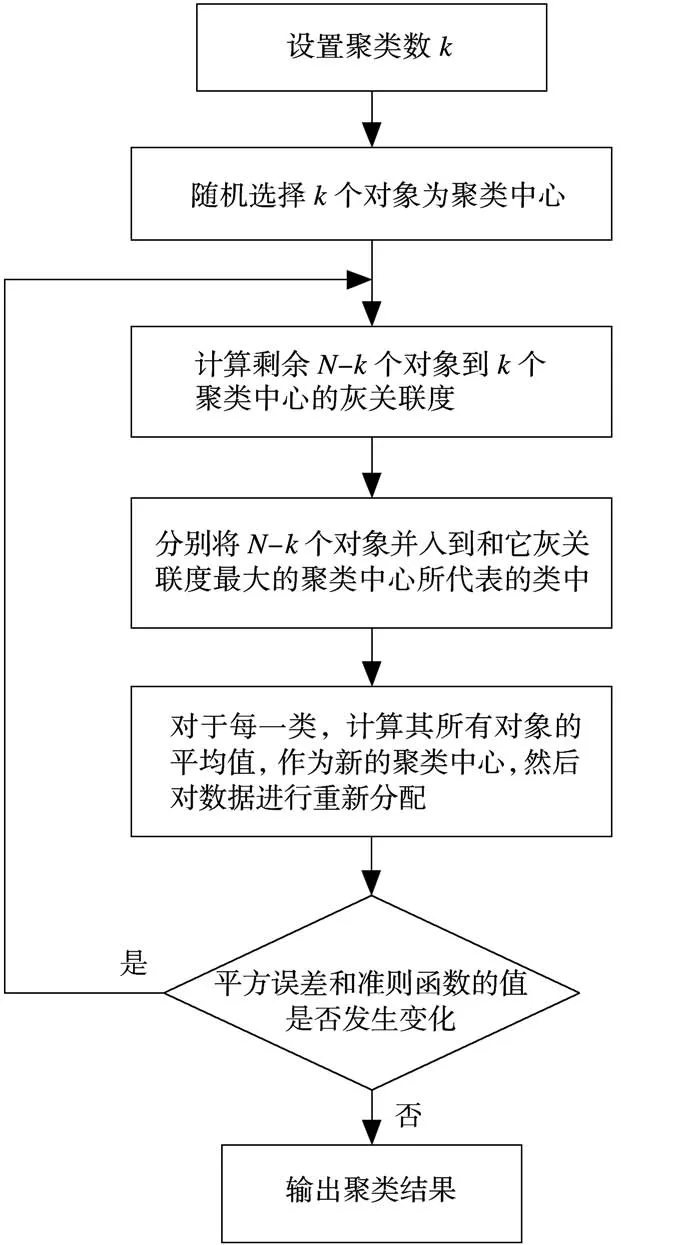
图2 改进的K-Means算法流程图

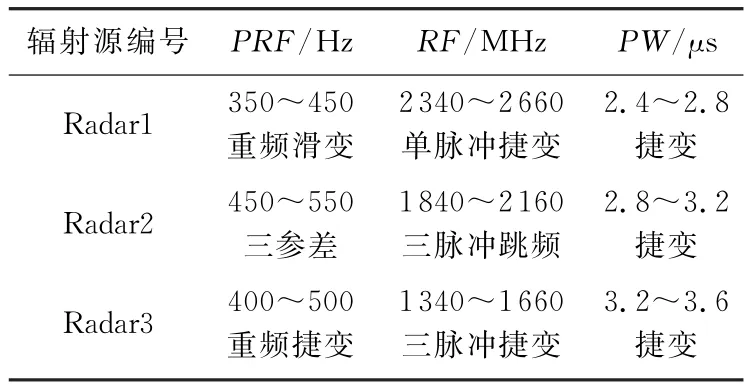
表1 雷达辐射源类型及参数设置

为了检验改进的K-Means算法分类方法能否对样本集Radar-database成功分类,使用该改进算法对样本集进行分类,观察分类结果。将分类结果和原始样本集进行对比,确定分类后每个样本的类别是否与原始样本集中该样本的真实类别相同,相同则称为分类正确,否则称为分类错误。

在分类之前,先定义能反映分类算法在特征关联上性能的参数如下:

(1)关联正确率:分类正确样本的个数占样本集中样本总数的比值即为关联正确率。

(2)关联错误率:分类错误样本的个数占样本集中样本总数的比值即为关联错误率。

(3)关联时间:每次算法运行的时间。

本文中的计算机仿真实验都是基于Matlab7.0的软件平台,硬件平台为以下配置的个人电脑:Celeron(R)CPU 3.06 GHz,512 MB内存。

3.2 聚类数k值的确定

首先使用改进的K-Means算法对样本集Radar-database进行聚类,由于算法要求分类前知道分类数目,采用试探法,让分类数k值从较小值逐步增加,对于每个选取的k值分别使用该改进的算法,输出聚类结果,计算聚类有效性指标的值。图3显示k值为2,3,4和5时,有效性指标值的大小。图4显示的是k值从2到10时,有效性指标值的大小,从图4可以看出当k值为3时,有效性指标值最大,样本集Radar-database最佳分为3类。

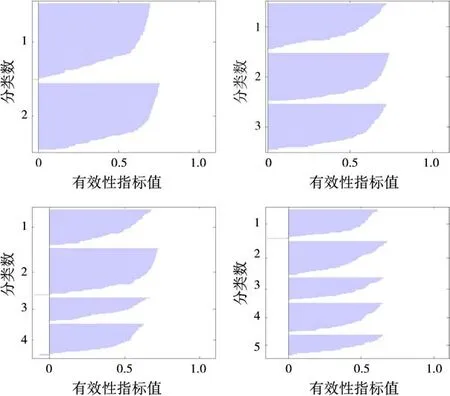
图3 k=2,3,4,5时有效性指标

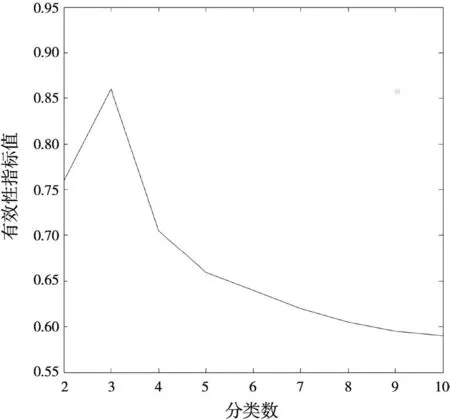
图4 有效性指标的最大值

3.3 改进的K-Means算法性能测试

用改进的K-Means算法对样本集Radar-database进行聚类,聚类结果如图5所示。由图5可知,改进的K-Means算法能对样本集Radar-database进行有效聚类,但由于样本集中部分样本存在重合和交叠,出现了一些分类错误的样本。图中黑色的点显示的就是分类错误的样本,共23个,关联正确率为92.33%。

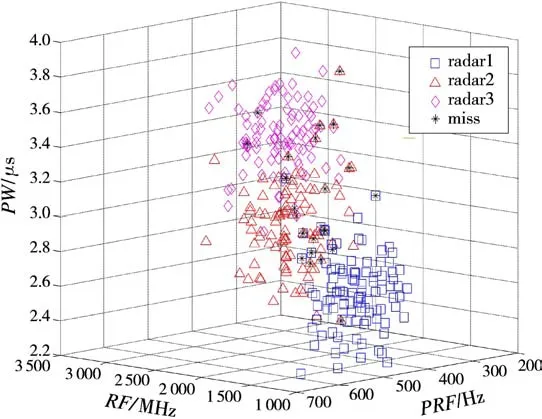
图5 样本集Radar-database分类结果

用改进的K-Means算法和K-Means算法进行比较,同时对样本集Radar-database进行100次分类,计算关联正确率和程序运行时间,数据见表2。

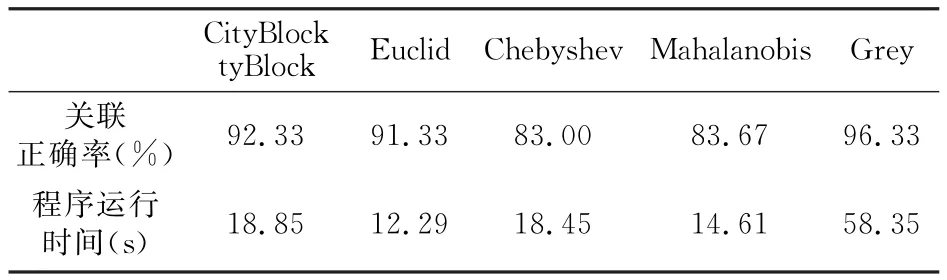
表2 改进的K-Means算法和K-Means算法性能比较

由表2可以看出改进的K-Means用灰关联度定义样本点间的距离,对样本集Radar-database进行聚类时,关联正确率高于K-Means算法中其他的距离定义,但程序运行时间明显提高,这是因为改进的K-Means算法的空间和时间复杂度都要高。

4 结束语

针对无源多传感器多辐射源特征关联问题,本文提出了一种改进的K-Means算法,用灰关联度定义了样本间的距离,在对样本集Radar-database进行分类时,可以有效地估计最优的分类数。仿真结果表明使用改进的K-Means进行分类时,关联正确率在96%以上,高于其他的度量方式,但消耗更多的时间,在实际应用时需要综合考虑。

[1]何友,王国宏,关欣.信息融合理论及应用[M].北京:电子工业出版社,2010:7-16,101-103.

[2]赵贵喜,王岩,于冰,等.基于人工鱼群聚类的雷达信号分选算法[J].雷达科学与技术,2013,11(4):375-378.ZHAO Gui-xi,WANG Yan,YU Bing,et al.Radar Signal Sorting Algorithm Based on Artificial Fish Swarm Clustering[J].Radar Science and Technology,2013,11(4):375-378.(in Chinese)

[3]Zhang Gexiang,Li Xu.A New Recognition System for Radar Emitter Signals[J].Kybernetes,2012,41(9):1351-1360.

[4]张红昌,阮怀林,龚亮亮,等.一种新的未知雷达辐射源聚类分选方法[J].计算机工程与应用,2008,44(27):200-202.

[5]张万军,樊甫华,谭营.聚类方法在雷达信号分选中的应用[J].雷达科学与技术,2004,2(4):219-223.ZHANG Wan-jun,FAN Fu-hua,TAN Ying.Application of Cluster Method to Radar Signal Sorting[J].Radar Science and Technology,2004,2(4):219-223.(in Chinese)

[6]Yang Zhutian,Wu Zhilu,Yin Zhendong,et al.Hybrid Radar Emitter Recognition Based on Rough KMeans Classifier and Relevance Vector Machine[J].Sensors,2013(13):848-864.

[7]苏锦旗,薛惠锋,詹海亮.基于划分的K-均值初始聚类中心优化算法[J].微电子学与计算机,2009,26(1):8-11.

[8]步媛媛,关忠仁.基于K-means聚类算法的研究[J].西南民族大学学报(自然科学版),2009,35(1):198-200.

[9]Wang Wenping,Wang Jiaoli,Huang Xinhuan,et al.Study on Community Structure Characteristics of Cluster Networks with Calculation and Adjustment of Trust Degree Based on the Grey Correlation Degree Algorithm[J].Grey Systems:Theory and Application,2011,1(2):129-137.