基于OFDM信号的二维全极化信息提取∗
刘 勇,梁 伟,王同权,周宏潮
(航天飞行器生存技术与效能评估实验室,北京100085)
0 引言
雷达目标高分辨和全极化信息在遥感成像、目标分类、识别等领域发挥着重要作用[1-3]。一方面,目标高分辨信息反映出长度、尺寸及外形等几何特征[1];另一方面,目标极化信息描述了表面粗糙度、对称度及空间指向等特征[2-3]。目前,主要有两种极化测量方法,分时极化测量和同时极化测量[4-5]。分时极化测量方法通过“交替发射、同时接收”两路极化信号,能够在相邻两个脉冲重复周期(PRI)内获取目标全极化信息。然而,由于目标运动将在极化散射矩阵(Polarization Scattering Matrix,PSM)两列之间引入去极化效应,该种极化测量方法不能准确获取非平稳运动目标的全极化信息。为此,学者研究了同时极化测量方法[5-7],通过正交极化通道“同时发射、同时接收”两路正交(准正交)编码信号,可仅在一个PRI内获取目标全极化信息[6-7]。Guili、王雪松等人深入研究了这种测量方法,法国ONERA设计的MERIC雷达系统采用这种方法获取飞机目标的全极化图像[8]。
然而,同时极化测量方法当前还主要应用在窄带领域,在目标全极化高分辨散射信息获取等方面的应用还不多。为此,本文基于全极化正交频率分集(Orthogonal Frequency Diversion Multiplex,OFDM)波形的基本原理[9],研究雷达目标二维高分辨全极化信息提取新方法。首先,建立了全极化OFDM信号的回波数据模型;然后,利用二维全极化MUSIC算法(2D P-MUSIC)得到目标的二维ISAR图像,以此提取各散射中心的极化散射矩阵;最后,利用某目标的暗室测量数据进行仿真试验,验证了该波形及相关信号处理方法的有效性。本文研究成果对于新体制宽带成像雷达系统研制具有重要参考意义。
1 回波数据模型
OFDM信号作为一种新的多载波波形,近年来在雷达目标检测、目标成像领域引起广泛关注[10-11]。当极化雷达正交通道同时发射两路具有不同调制特性的OFDM信号时,便得到了全极化OFDM信号[9]。设雷达天线为水平(H)和垂直(V),则H、V极化通道的两路基带调制信号为
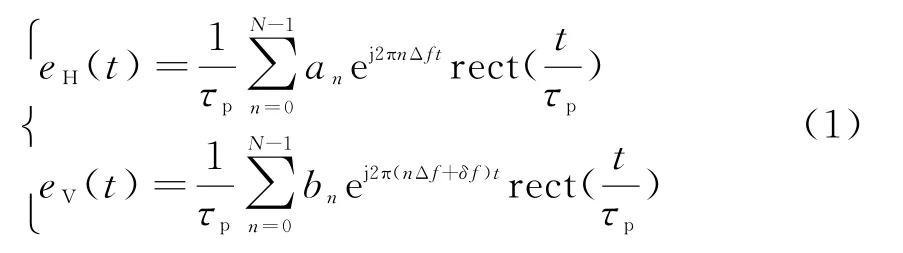
式中,Δf为测量频率间隔,信号带宽B=K·Δf;δf为H、V极化通道的子载波频率间隔;a n和b n两个调制序列,|a n|=|b n|=1,n=0,…,N-1;rect(t/τp)为脉宽τp的矩形脉冲包络,即
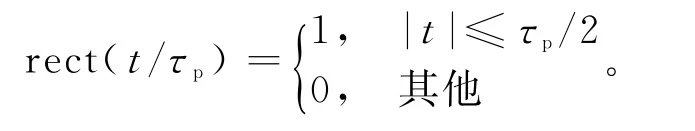
为降低OFDM波形的峰值平均功率比(PAPR),H、V极化通道的第n个子载波复加权系数分别取[11]
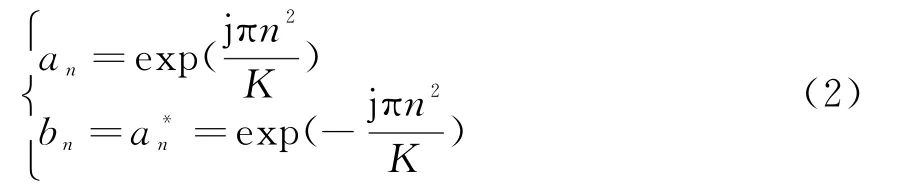
对式(1)中的基带信号进行傅里叶变换,可得到两路信号频谱为
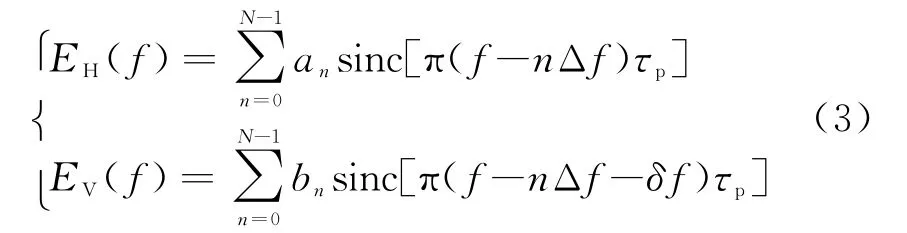
其中,sinc(x)=sin(x)/x。
为满足子载波正交性,Δf、δf均取1/τp的整数倍,且Δf>δf。由辛克函数的性质可知,全极化OFDM波形的频谱特性满足
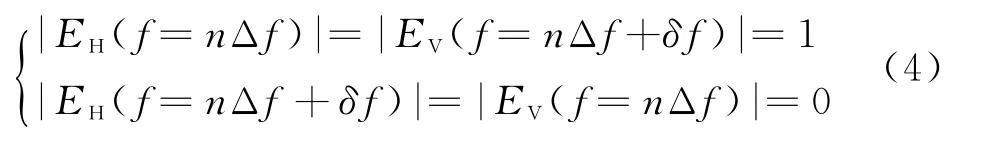
在实际应用中,目标运动或系统频率漂移将引入额外的频差,破坏子载波正交性,子载波之间的互扰影响不能完全消除。经分析可知,频差会对全极化采样数据产生两方面影响:一是采样值幅度减小,减小量为sinc(πf d,kτp);二是不同极化通道的采样值产生互扰,互扰量为sinc π(δf+f d,k)τp。
在光学区,雷达目标的散射特性可以用散射中心模型来近似描述[1]。对于转台目标成像,其场景如图1所示。
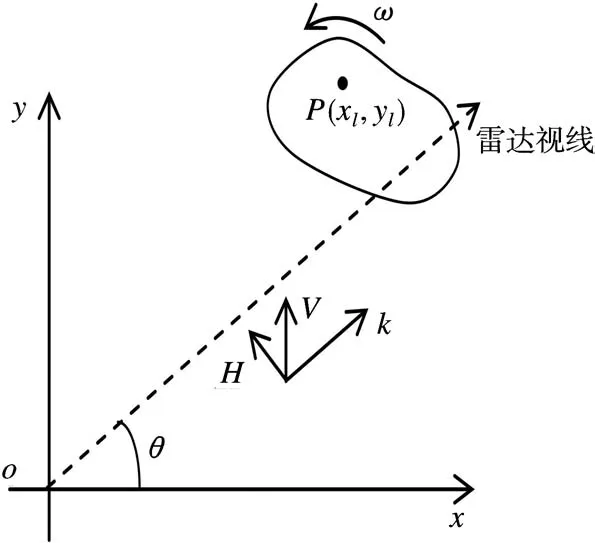
图1 转台目标成像示意图
设目标由L个散射中心构成,第l个散射中心的坐标值为(x l,y l),l=1,…,L,在频率f、观测角度θ下,目标全极化响应近似为
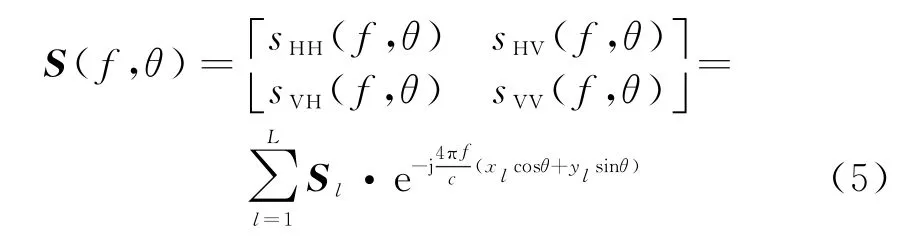
设射频频率为fc,则两路接收信号的基带频谱为

式中,nH(f,θ)和nV(f,θ)为H、V两路极化通道的噪声。
设转台成像角度范围为Θ,角度增量为Δθ=Θ/M,第m个观测角度为θm=mΔθ。在该观测角度下,四个采样值可通过对RH(f,θ)和RV(f,θm)在频点f n=nΔf和f n+δf=nΔf+δf处得到,写成矩阵形式为
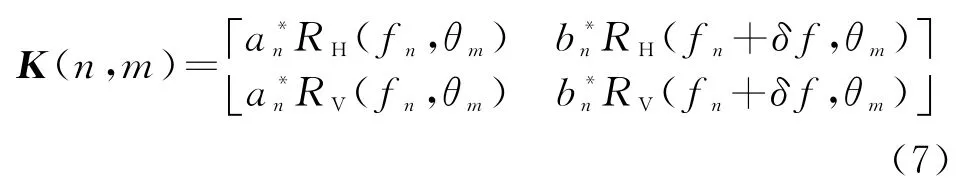
基于式(4)中的子载波正交特性,可以消除两个极化通道信号EH(f n)与EH(f n+δf),以及EV(f n)EH(f n)与EV(f n+δf)之间的互扰,式(7)可表示为
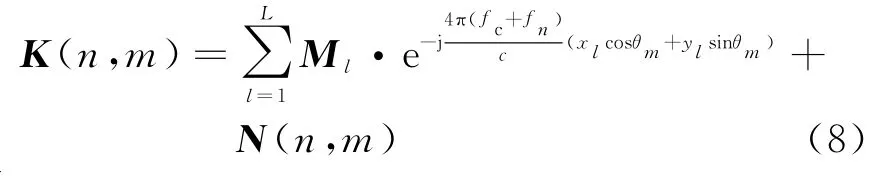
式中,
以上数据模型是在“频率-角度”域内的离散表达形式,通过二维插值可得到其在二维笛卡尔系下的表达式,即将f,θ表示为,得到
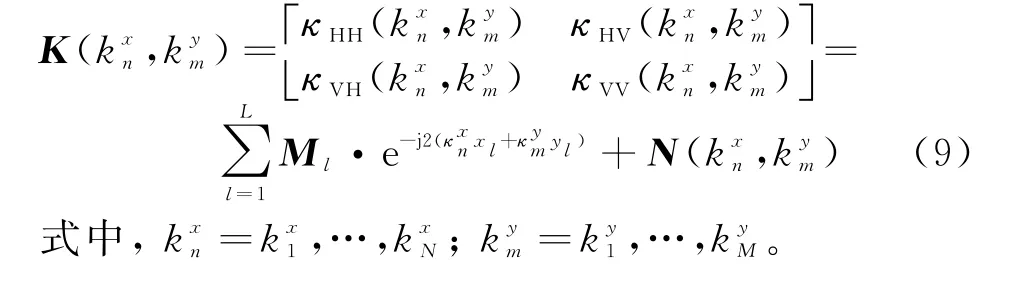
2 二维极化MUSIC算法
将式(9)表示成矩阵形式,得到
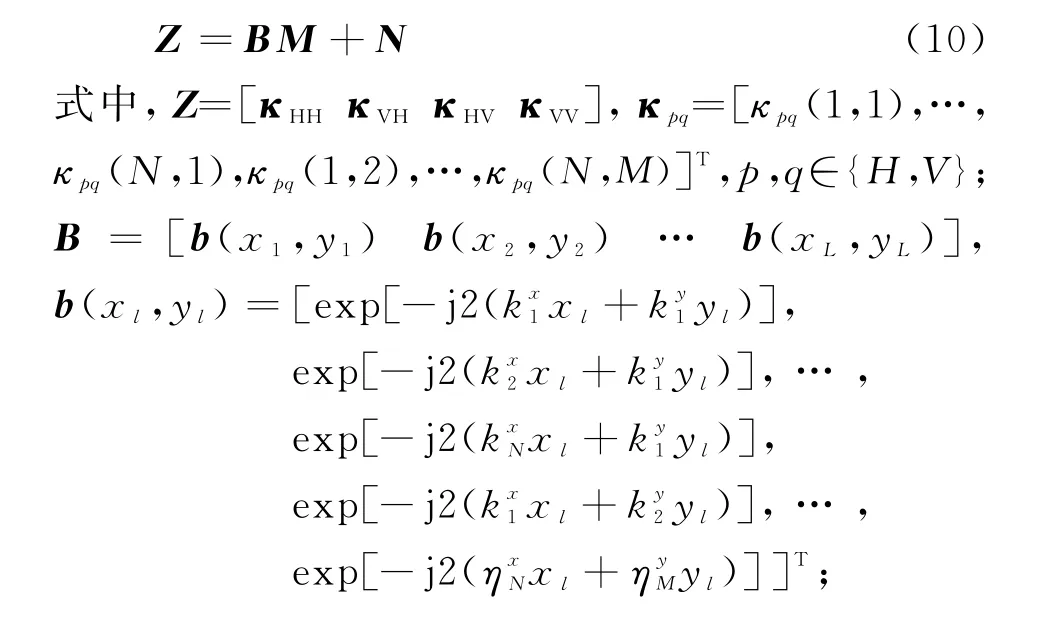
利用上式中的数据模型,得到目标全极化ISAR像,进而可提取出目标散射中心全极化信息。一种简单的方法是对四路极化通道数据分别进行二维逆傅里叶(IFFT)变换;另一种方法是利用参考文献[12-13]中的二维M USIC算法,二维MUSIC算法处理流程如下:
第1步,利用四路极化通道的频域采样数据,得到极化相干矩阵估计值;
第2步,对进行特征值分解,得到

式中,D=diag{λ1,λ2,…,λNM},λ1≥λ2≥ …≥λNM为NM个特征值;U=[u1,u2,…,u NM]为对应的特征向量矩阵。
对NM个特征值排序,得出目标散射中心数量估值,这样,由前个特征向量构成信号子空间,即E S=[u1,…,u L],由另外NM-L个特征向量构成噪声子空间,即E N=[u L+1,…,u NM]。
第3步,利用式(10)中的形式构造搜索向量b(x,y),从而得到目标全极化ISAR像为
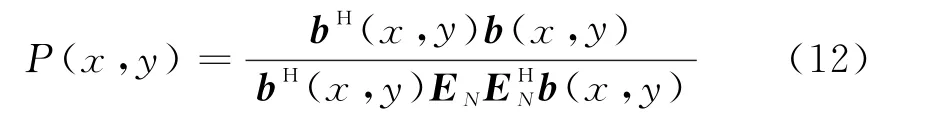
第4步,通过搜索P(x,y)中的峰值点,可估计散射中心的坐标值,即。然后,形成导向矢量,…,,由最小二乘算法得到全部散射中心的极化散射矩阵估计值,如下:

3 仿真结果
利用某目标模型的暗室测量数据进行了仿真试验,验证全极化OFDM信号及相关信号处理算法的有效性。目标模型几何结构尺寸如图2所示[14],测量频率范围为10~11 GHz,频率步进为5 M Hz,测量俯仰角、滚动角均为0°,方位角范围为-30°~+30°,角度步进为0.2°。
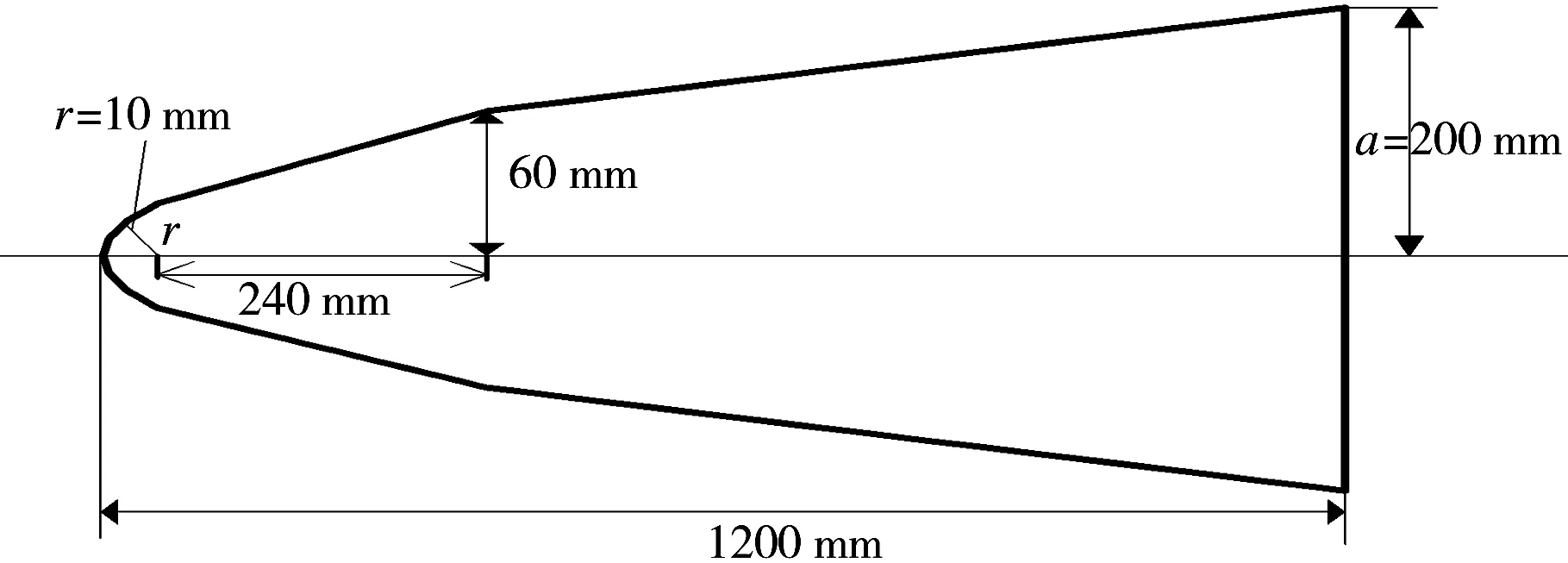
图2 测量目标的几何尺寸
全极化OFDM信号的参数设计如下:τp=10μs,Δf=100/τp=10 M Hz,δf=50/τp=5 M Hz,N=100,信号带宽B=1 GHz。目标成像角度范围为-5°~5°,在Θ=10°的成像角度范围内共有50个角度采样值,角度步进值Δθ=Θ/50=0.2°。图3给出了由二维极化MUSIC算法得到的目标ISAR像,其中SNR=5 d B,目标速度v0=0 m/s。
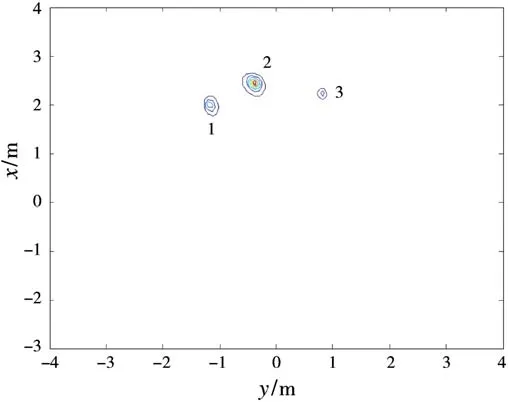
图3 二维极化MUSIC算法得到的ISAR像
显然,在图3中可提取出目标散射中心,得到三个散射中心的极化散射矩阵估计值,如下:

同时,为分析目标径向运动对OFDM信号性能的影响,对H和V极化通道的第k个子载波调制如下的相位项,即
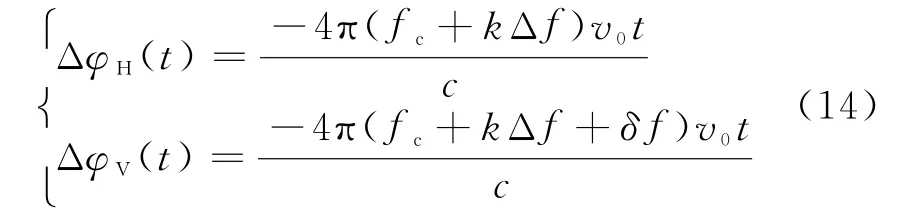
在不同目标运动速度情况下,极化散射矩阵的测量值也将不同。例如,当v0=400 m/s时,三个散射中心极化散射矩阵的测量值如下:

为评估目标运动对极化散射矩阵测量值的影响,定义如下的评估参数。
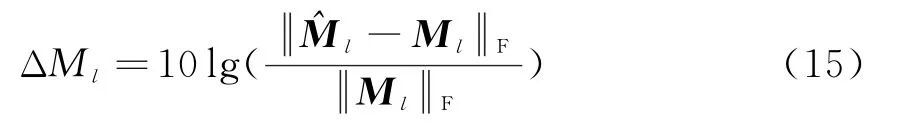
式中,M l为无噪声测量值(真实值);为在不同速度下的测量值;表示矩阵F-范数。
图4给出了在不同目标速度时,三个散射中心的测量性能,其中,SNR=5 dB,速度范围取0~600 m/s。显然,当目标运动速度增大时,测量误差变大,例如,当v0=0 m/s时,ΔM1=-59.87 dB(散射中心1),ΔM2=-52.18 dB(散射中心2),ΔM3=-40.63 dB(散射中心3);当v0=400 m/s时,ΔM1=-18.12 dB(散射中心1),ΔM2=-18.89 dB(散射中心2),ΔM3=-20.17 dB(散射中心3)。

图4 在不同速度下的极化散射中心提取性能
4 结束语
基于全极化OFDM波形的基本原理,研究了提取目标二维散射中心全极化信息的新方法。在构建回波数据模型的基础上,利用二维极化MUSIC算法得到超分辨散射中心的极化散射矩阵,仿真试验结果验证了相关信号处理算法的有效性。该全极化波形的成像数据率提高了一倍,可扩展应用于极化合成孔径雷达(Pol-SAR)、极化逆合成孔径雷达(Pol-ISAR)等不同应用领域 。
[1]Cloude S R,Pottier E.A Review of Target Decomposition Theorems in Radar Polarimetry[J].IEEE Trans on Geoscience and Remote Sensing,1996,34(2):498-518.
[2]程旭,马梁,李永祯,等.弹道目标极化特征可分性研究[J].雷达科学与技术,2011,9(5):457-463.CHENG Xu,MA Liang,LI Yong-zhen,et al.Research on the Separability of Ballistic Targets’Polarimetry Characteristics[J].Radar Science and Technology,2011,9(5):457-463.(in Chinese)
[3]庄钊文,肖顺平,王雪松.雷达极化信息处理及其应用[M].北京:国防工业出版社,1999:113-123.
[4]Giuli D,Fossi M,Facheris L.Radar Target Scattering Matrix Measurement Through Orthogonal Signals[J].IEE Proceedings of Radar and Signal Processing,1993,140(4):233-242.
[5]Howard S D,Calderbank A R,Moran W.A Simple Signal Processing Architecture for Instantaneous Radar Polarimetry[J].IEEE Trans on Information Theory,2007,53(4):1282-1289.
[6]李棉全,李永祯,王涛,等.一种新的全极化雷达信号处理方案设计[J].雷达科学与技术,2009,7(2):119-123.LI Mian-quan,LI Yong-zhen,WANG Tao,et al.A New Signal Processing Mechanism for Full Polarimetric Radar[J].Radar Science and Technology,2009,7(2):119-123.(in Chinese)
[7]Babur G P,Ligthart L P.Wideband Ambiguity Matrix of LFM-Signals Used in Polarimetric Radar Allowing Simultaneous Measurement of Scattering Matrix Elements[C]∥Proceedings of the European Radar Conference,Amsterdam:[s.n.],2008:128-131.
[8]Titin-Schnaider C,Attia S.Calibration of the MERIC Full-Polarimetric Radar:Theory and Implementation[J].Aerospace Science and Technology,2003,7(8):633-640.
[9]刘勇,李永祯,王雪松.基于正交频率分集的目标全极化瞬时测量方法[J].系统工程与电子技术,2009,31(11):2587-2591.LIU Yong,LI Yong-zhen,WANG Xue-dong.Target Full Polarization Instantaneous Measurement Based on Orthogonal Frequency Division[J].Systems Engineering and Electronics,2009,31(11):2587-2591.(in Chinese)
[10]Berger C R,Demissie B,Heckenbach J,et al.Signal Processing for Passive Radar Using OFDM Waveforms[J].IEEE Journal of Selected Topics in Signal Processing,2010,4(1):226-238.
[11]Paichard Y,Castelli J C,Dreuillet P,et al.HYCAM:A RCS Measurement and Analysis System for Time-Varying Targets[C]∥Proceedings of the IEEE Instrumentation and Measurement Technology Conference,Sorrento:[s.n.],2006:921-925.
[12]Kim K T,Kim S W,Kim H T.Two-Dimensional ISAR Imaging Using Full Polarization and Super-Resolution Processing Techniques[J].IEE Proceedings of Radar,Sonar and Navigation,1998,145(4):240-246.
[13]Dai Da-hai,Luo Jia,Liu Zhong-xun,et al.Fully Polarized Radar Target Scattering Center Extraction[C]∥1st Asian and Pacific Conference on Synthetic Aperture Radar,Huangshan,China:[s.n.],2007:159-163.
[14]李永祯,程旭,李棉全,等.极化信息在雷达目标检测中的得益分析 [J].现代雷达,2013,35(2):35-39.LI Yong-zhen,CHENG Xu,LI Mianquan,et al.A Study on Polarization Gain for Radar Targets Detection[J].Modern Radar,2013,35(2):35-39.(in Chinese)

