一种有效的穿墙雷达成像杂波抑制算法∗

赵中兴,孔令讲,贾 勇,李志希

(电子科技大学电子工程学院,四川成都611731)

0 引言

穿墙雷达能够发射电磁波透过墙体、门以及其他非透明材料等障碍物探测到隐藏的目标,在公安防暴、反恐斗争、灾难救援及城市巷战中具有广泛的应用前景。一部可靠的穿墙雷达成像系统必须能够实现对墙后目标的成像、检测、定位和跟踪,近些年来,穿墙雷达成像(TWRI)已经成为国内外雷达应用领域的一个研究热点[1-4]。

在TWRI的应用中,信号在墙体内的传输过程中能量发生衰减,导致目标回波十分微弱,甚至在图像上完全湮没临近墙体的静止目标,无法有效辨别出目标,因此,杂波抑制成为临近墙体的静止目标成像中的关键问题之一。为了解决上述问题,早期一些学者进行了深入的研究,并提出了许多背景杂波抑制算法。文献[5-7]提出了在已获得先验信息的前提下采用背景对消的方法来抑制背景杂波,这些算法的核心是墙体扩展函数的估计问题,但实际环境的复杂性如墙体表面不均匀、天线位置误差、多径干扰等因素给墙体杂波的估计带来很大误差,导致背景对消法在实测环境下性能明显下降,甚至失效。美国维纳诺瓦大学的学者Yoon提出利用空域滤波的方法抑制墙体杂波[8],但实际环境的复杂性同样会导致目标回波和墙体杂波的空间谱在零频附近的公共频带展宽,造成严重的目标损耗。

近些年来,基于统计信号处理如主成分分析(PCA)、独立成分分析(ICA)、因素分析(FA)和奇异值分解(SVD)等的杂波抑制算法成为研究热点,并被广泛应用到TWRI中[9-14],其中PCA和SVD由于复杂度低、计算量小,因此应用最多。但这些基于统计信号处理的方法通常会带来一个问题:如何有效确定门限值。例如SVD,它通常对接收信号的B-扫矩阵进行分解,将信号空间分成三部分:杂波子空间、目标子空间和噪声子空间。印度学者Verma认为第一个特征成分表征杂波回波,第二个特征成分表征目标回波,其余特征成分表征噪声;澳大利亚学者Tivive提出利用空场景奇异值分布的先验,将目标场景与空场景的奇异值进行对消来确定子空间的界限。但在TWRI的实际应用中,这些方法的性能严重下降,因为场景的先验信息未知,且杂波的成分非常复杂,能量也强弱不一,其中,墙体杂波和直耦信号的能量较强,多径幻象、地面反射波、目标栅瓣等杂波的能量很弱,因此,能够将杂波与目标回波完全分离的门限是很难确定的。目前国内TWRI的杂波抑制方面还比较落后,本文在这些基于统计信号处理的杂波抑制算法的基础上作改进,提出一种有效的两阶段杂波抑制算法:首先在SVD的基础上提出一种简单有效的方法确定门限值,在保留全部目标信息的前提下最大程度地抑制强杂波;然后对第一阶段的成像结果进行图像增强处理,抑制弱杂波和噪声,突显目标信息。

本文第1节首先简要介绍TWRI模型,然后介绍两阶段杂波抑制算法的原理与实现过程,第2节给出实测数据成像结果及分析,第3节是结束语。

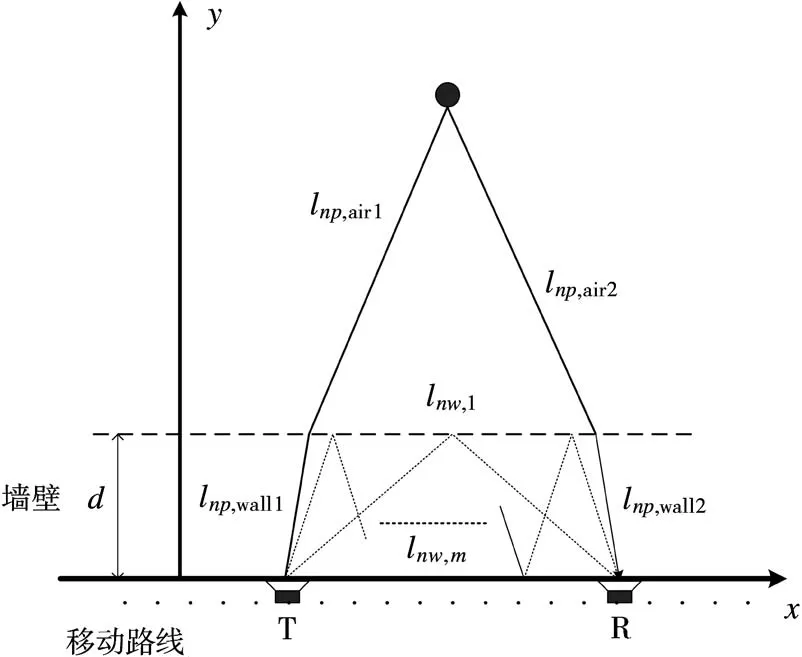
图1 TWRI几何模型

1 算法原理与实现

1.1 穿墙雷达成像

成像模型如图1所示。假设墙体是厚度为d、介电常数为ε的理想均匀介质,TWRI系统天线为单发单收、沿x轴依次移动、间隔为l的均匀线阵,合成阵元的数目为N,发射天线的位置为x n(n=1,2,…,N),收发天线的间距为r。

雷达发射的信号为包含K个频点的步进频信号合成超宽带信号,起始频率为w0,步进间隔为Δw,即w k=w0+kΔw,k=0,1,…,K-1,目标位于x p=(x p,z p),散射系数为σp,第n次扫描的接收回波为

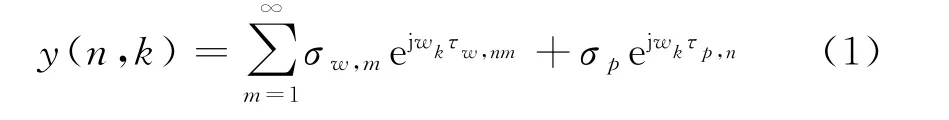
式中,σw,m是发射电磁波经过墙体后表面m次反射后被接收的墙体反射波的散射系数,τw,nm是发射天线发射的电磁波经过墙体后表面的m次反射后回到接收天线的延时,τp,n是在第n个位置上发射信号经过位于x p的点目标散射后回到接收天线的延时,它们分别表示为

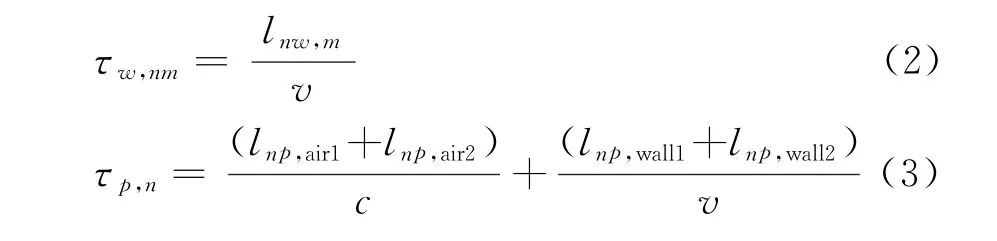
式中,c表示真空中的光速;表示电磁波在墙体内的传播速度;表示经过墙体后表面m次反射后的回波信号在墙体内的传输距离;l np,air1,l np,wall1分别表示发射信号在自由空间和墙体中的传输距离;l np,air2,l np,wall1分别表示目标反射信号在自由空间和墙体中的传输距离。

成像区域按距离向和方位向共划分为Q个像素点,根据步进频信号的反向投影(BP)成像算法原理,首先对步进频率复信号进行脉压(IFFT)变换到时域上,然后依次计算出每个像素点到天线的延时进行BP成像,所以像素点x p的像素为

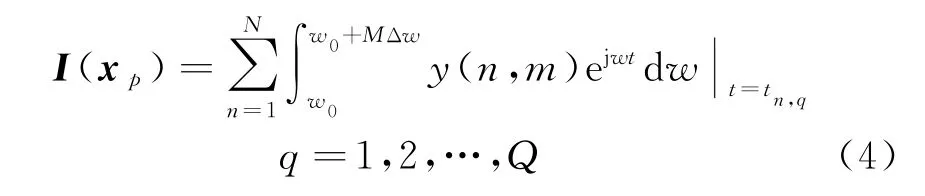
1.2 杂波抑制

临近墙体目标的成像和检测是TWRI的热点研究方向之一,因为信号传输过程中能量严重衰减,导致目标回波非常微弱,目标图像甚至完全湮没在杂波图像中,造成目标在场景图像上的丢失,因此,杂波抑制成为临近墙体目标成像的关键问题。本文提出的杂波抑制算法,分别在回波域和图像域进行前后两个阶段的杂波抑制处理,其基本思想是利用能量上的差异将回波信号空间分解为两部分:强杂波子空间和弱杂波、目标和噪声混合子空间,采用一种基于图像对比度的新方法有效确定它们的界限,提取出包含目标信息的混合子空间,再对成像结果进行图像增强处理,抑制弱杂波和噪声,提取出清晰的目标图像。

1.2.1 强杂波抑制

SVD在数学上用来提取矩阵的重要特征,将一个复杂矩阵分解为一系列子矩阵,子矩阵描述的是矩阵的重要特征。SVD在2008年由国外学者Chandra首次引入TWRI中抑制杂波。该算法主要是利用SVD的物理特性,即奇异值的大小决定对应特征成分的重要性,抑制强杂波子空间,有效保留目标信息,其最大的优越性在于算法复杂度低,计算时间短。

假设穿墙雷达的B-扫回波矩阵表示为

式中,b n是1×K的列向量,表示穿墙雷达系统在第n个位置接收到的步进频回波信号,共有K个频点,即

通过SVD处理,原始回波矩阵B的特征结构可以表示为

式中,U=[u1,u2,…,u M]和V=[v1,v2,…,v M]是酉矩阵,其列矢量分别是BBH,BHB的特征矢量。D的上部分是N×N的对角矩阵,对角线元素是依次递减的奇异值,D11≥…≥D NN,因此,B可以表示为所有特征成分的线性组合:

式中,E n表示第n个特征成分,σn=D nn是第n个奇异值。

将信号空间划分为强杂波子空间和目标、弱杂波及噪声的混合子空间两部分:

式中,E C表示强杂波子空间,E P表示目标、弱杂波及噪声的混合子空间,强杂波抑制也就转化为子空间的划分问题,即寻求有效的方法来确定奇异值的门限。

通常情况下,奇异值的分布除了受背景的影响,还与目标的个数、位置及散射系数有关[15],单凭奇异值的分布特性很难确定其门限,本文提出一种基于图像对比度的方法来确定门限值,有效提取出包含全部目标信息的混合子空间。在TWRI中,常用的图像对比度衡量准则很多,本文就采用标准差与均值之比来表征图像的对比度,其实现步骤如下:

1)直接对回波矩阵B采用BP算法进行成像,获取原始信号的B-扫图像I(0):

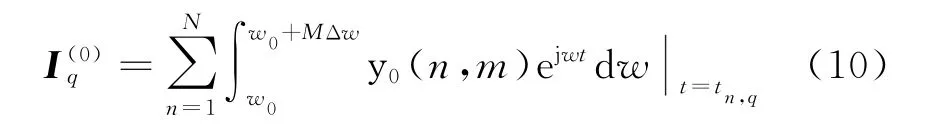
式中,y0(n,m)即为原始回波信号y(n,m),原始图像的对比度为

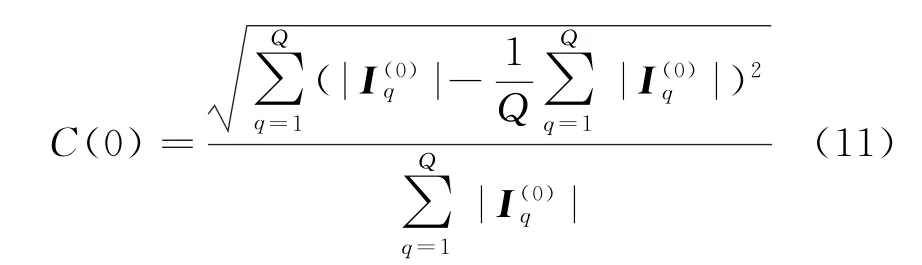
2)假定E1→n是要抑制的杂波子空间(初始时n=1),目标子空间E n+1→N记为

类似1),E n+1→N对应的图像及其对比度为

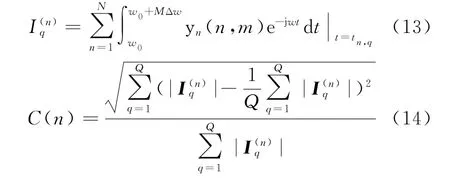
3)计算对比度C(n)的二阶逆向差分:

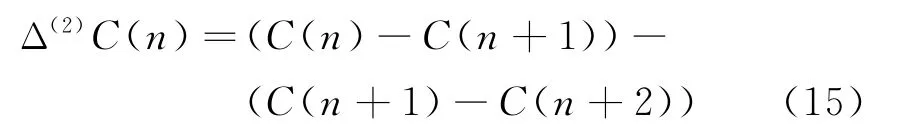
4)检查杂波子空间的维数n:如果n≤N-2,转至2);否则,停止。

5)在关于n的函数Δ(2)C(n)中,从n=1开始依次搜索,直至寻找到极大值Cpeak为止,对应的奇异值σpeak即为所求门限。

上述的门限值确定方法,实质上是通过衡量特征成分对图像对比度的影响来判定其归属,对比度的差分就是对应特征成分被抑制后图像对比度的改变量,二次差分函数能够表征对比度改变量的变化趋势,极大值的出现说明对比度改变量急剧减小,即对比度趋于稳定,这意味着强杂波已经被抑制,该位置可认为是两个子空间的边界。

1.2.2 图像增强

经过强杂波抑制后,场景图像仍然分布着大量的杂波斑。为了改善视觉效果,有必要进行图像增强,突出目标信息。PCA是回波域上广泛采用的一种杂波抑制方法,实质上是根据能量的大小将样本矩阵投影到多维空间中相互正交的坐标轴上,按照能量损失最小的原则来降低维度。本文将回波域SVD处理后的图像作为样本矩阵,每行为一个样本,每列为一个维度,通过PCA处理,提取出最能够代表目标信息的特征成分,消除那些“冗余”的数据,进一步地提高了图像的信杂比。

假设m,n分别是距离向和方位向的像素点索引 ,样本矩阵I表示为

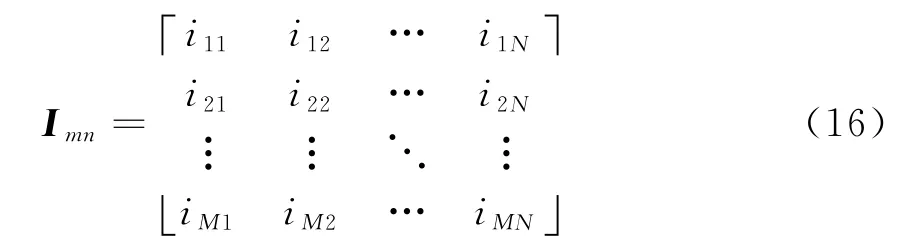
I的N个主成分可以表示为

式中,A为M×M的投影矩阵,I将转化为F,F的列矢量就是所谓的主成分,I的协方差矩阵为,经过对角化处理,可以分解为不同的特征成分的线性叠加:

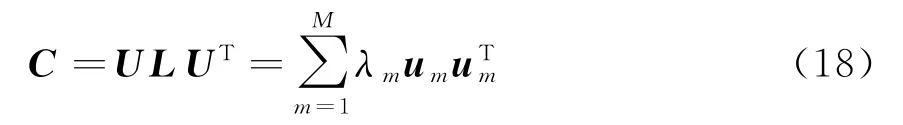
式中,L是对角元素为特征值的对角矩阵,即L jj=λj(j=1,2,…,M),且λ1≤ … ≤λM,U为正交特征矩阵,可以表示为U=[u1,…,u M],u M是对应于λm的特征向量。

事实上,对称矩阵的对角化就是找到一个正交矩阵,满足条件:UTCU=L,假定通过PCA处理后的图像矩阵为F,显然,F中各个维度的协方差为零,即

因此,I=UF可以分解为

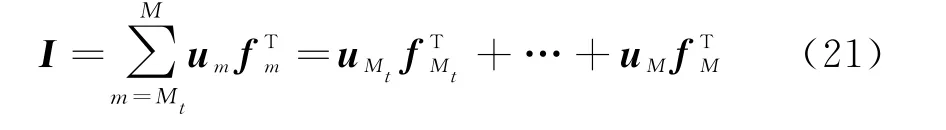
经过强杂波抑制后,目标在场景图像中已经显现出来,其能量要高于弱杂波和噪声,这决定了能量较大的特征成分归属于目标子空间,因此,门限值M t可以直接根据特征值的幅度分布来确定,在特征值的差分函数Δλ(m)中,从m=1开始依次搜索,直至寻找到由急剧下降到平稳变化的临界点M b,即为所求门限值。

2 实验结果分析

实验场景和TWRI系统如图2所示。系统采用频率为1～2 GHz的超宽带步进频信号,频点数N=501,频率步进间隔Δf=2 MHz,单个频点脉冲持续时间为100μs,两个带宽为500 MHz～3 GHz、波束宽度为60°的定向天线紧贴墙壁来发射和接收信号,合成阵列的长度为4 m,间隔为10 cm。选择合成阵列正前方4 m×4 m的区域进行成像,两个尺寸均为20 cm×30 cm的小铝板用来模拟人体目标放置在距离合成阵列的起始点1 m和2.5 m位置,分别距离墙壁2.5 m和3 m,墙体的厚度和介电常数均未知。

由于天线间的直接耦合和墙体反射的信号能量远大于目标反射回波的能量,利用BP算法直接对原始回波信号进行成像,则场景成像结果如图3所示,杂波图像占主导,目标图像完全湮没在杂波图像中。目标场景的奇异值分布曲线如图4所示,可以发现,奇异值稳定地减小直至趋于零,仅由奇异值分布曲线很难直接判定出两个子空间的界限。应用1.2.1节描述的基于图像对比度的门限确定方法来划分强杂波与包含目标信息的混合子空间,图5为图像对比度曲线(采用标准差与均值之比表征图像对比度),从图6图像对比度的二阶逆向差分曲线可以判定P点即为奇异值的门限。图7为强杂波抑制后的成像结果,可以看出,场景图像仍然分布大面积的弱杂波和噪声,仍然对目标的检测造成一定程度的干扰。

图2 实验场景和TWRI系统

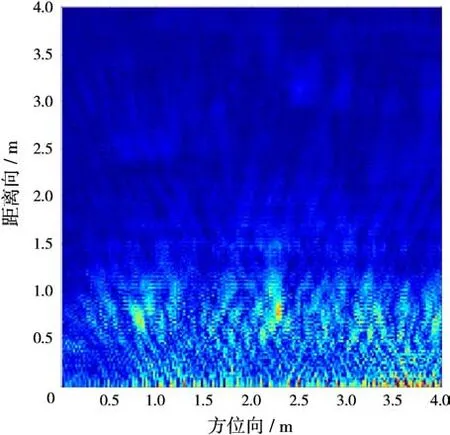
图3 原始场景图像

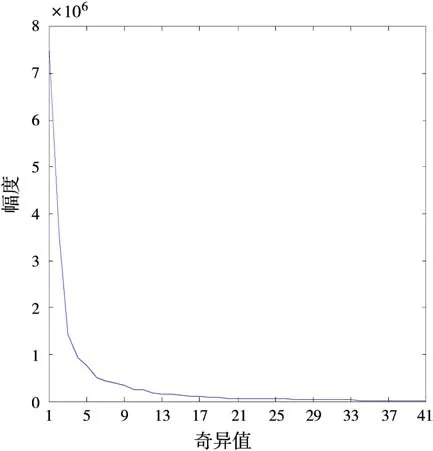
图4 奇异值分布曲线

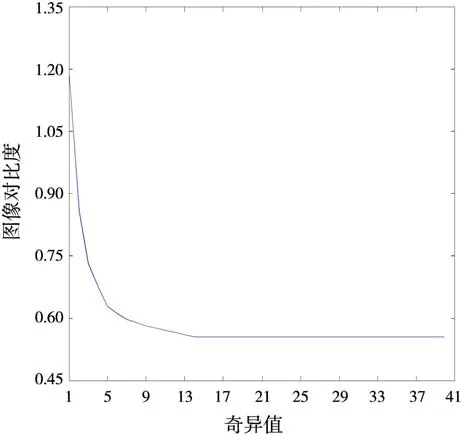
图5 图像对比度分布曲线图

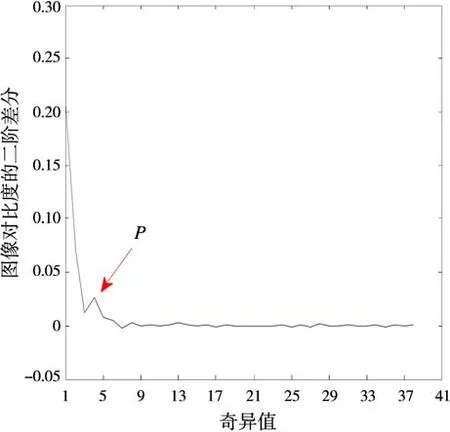
图6 图像对比度的二阶逆向差分曲线

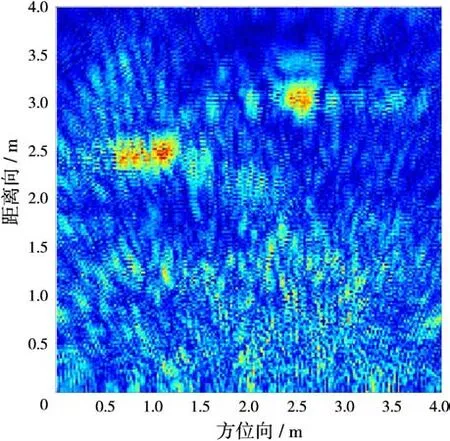
图7 强杂波抑制后的场景图像

下一步是对强杂波抑制后的图像进行增强处理,图8为初始的场景图像的特征值分布曲线,目标图像占据主要的特征成分,应用1.2.2节中基于特征值幅度分布的方法确定其门限,从图9特征值的差分分布曲线中可以判定L点为门限,提取出目标图像,如图10所示。

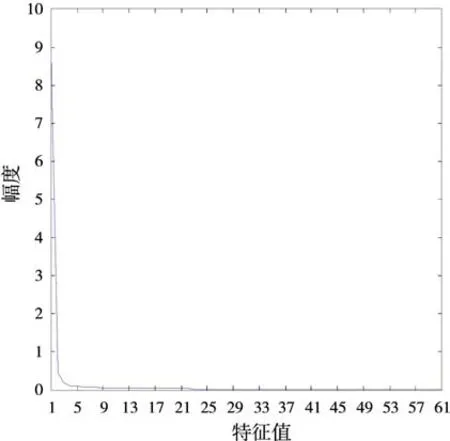
图8 原始图像的特征值分布曲线

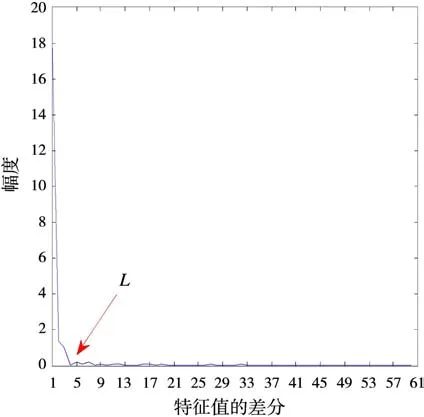
图9 特征值的差分分布曲线

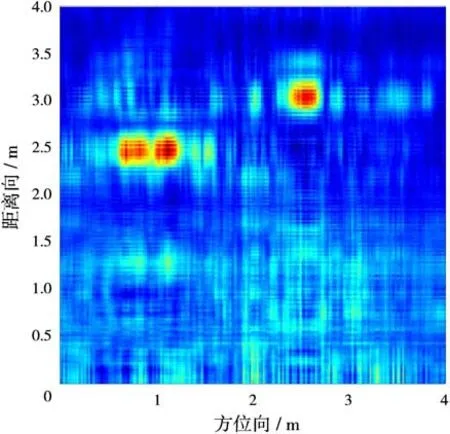
图10 最终场景图像

可见,杂波得到了一定程度的抑制,场景图像得到大大改善,为了量化说明,引入场景图像信杂比的定义,将目标图像的最大值作为目标强度,整幅场景图像的均值作为杂波强度,表达式如下:

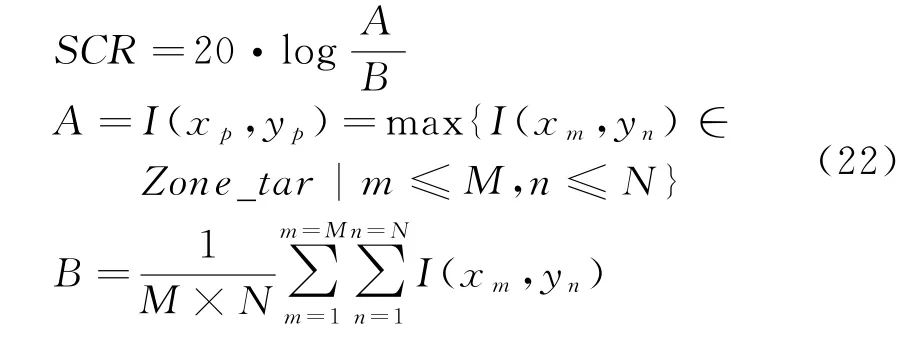
式中,M,N分别表示图像在方位向和距离向的像素点数目;I(x m,y n)表示场景图像在(x m,y n)的像素值;Zone_tar表示目标图像区域;A表示目标图像的强度;B表示杂波图像的强度。经计算,原始场景图像的SCR为17.1 dB,经过杂波抑制后最终场景图像的SCR为31.9 dB,即该杂波抑制算法将场景图像的信杂比提升了约15 d B。

3 结束语

本文针对临近墙体目标成像问题,分析了实际环境中背景杂波的特点,提出了两阶段杂波抑制算法,即首先把基于图像对比度的门限确定方法引入到SVD中抑制强杂波,然后应用基于PCA的图像增强算法从目标、噪声和弱杂波的混合图像中提取出目标图像。通过对实验数据的处理效果可以看出,该算法能够很好地处理实测环境下微弱目标的图像被杂波和噪声图像湮没的问题,准确地提取出目标图像,实现对临近墙体目标的精确成像。

[1]Nag S,Fluhler H,Barnes M.Preliminary Interferometric Images of Moving Targets Obtained Using a Time-Modulated Ultra-Wide Band Through-Wall Penetration Radar[C]∥Proceedings of the IEEE Radar Conference,Atlanta,GA:[s.n.],2001:64-69.

[2]Ahmad F,Amin M G,Kassam S A.Synthetic Aperture Beamformer for Imaging Through a Dielectric Wall[J].IEEE Trans on Aerospace and Electronic Systems,2005,41(1):271-283.

[3]王涵宁,陆必应,周智敏,等.基于墙体参数估计的穿墙成像与校正算法[J].雷达科学与技术,2011,9(5):430-436.WANG Han-ning,LU Bi-ying,ZHOU Zhi-min,et al.An Algorithm of Through-Wall Imaging and Correction Based on the Estimation of Wall Parameters[J].Radar Science and Technology,2011,9(5):430-436.(in Chinese)

[4]Seng C H,Amin M G,Ahmad F,et al.Segmentations of Through-the-Wall Radar Images[C]∥IEEE Radar Conference,Atlanta,GA:[s.n.],2012:647-652.

[5]Amin M G,Estephan H.An Adaptive Background Estimation Technique for Enhancing Target Detection in Through-the-Wall-Radar Imaging Applications[C]∥Proceedings of SPIE,Orlando,Florida,USA:[s.n.],2009:6-10.

[6]Chang P C,Burkholder R J,Volakis J L.Adaptive CLEAN with Target Refocusing for Through-Wall Image Improvement[J].IEEE Trans on Antennas and Propagation,2010,58(1):155-162.

[7]Chang P C,Burkholder R J,Volakis J L.Through-Wall Building Image Improvement via Signature-Based CLEAN[C]∥IEEE Antennas and Propagation Society International Symposium,SanDiego,CA:[s.n.],2008:1-4.

[8]Yoon Y S,Amin M G.Spatial Filtering for Wall-Clutter Mitigation in Through-the-Wall Radar Imaging[J].IEEE Trans on Geoscience and Remote Sensing,2009,47(9):3192-3208.

[9]Chandra R,Gaikwad A N,Singh D,et al.An Approach to Remove the Clutter and Detect the Target for Ultra-Wideband Through-Wall Imaging[J].Journal of Geophysics and Engineering,2008,5(4):412-419.

[10]Verma P K,Gaikwad A N,Singh D,et al.Analysis of Clutter Reduction Techniques for Through Wall Imaging in UWB Range[C]∥Progress In Electromagnetics Research B,[s.l.]:[s.n.],2009:29-48.

[11]Gaikwad A N,Singh D,Nigam M J.Application of Clutter Reduction Techniques for Detection of Metallic and Low Dielectric Target Behind the Brick Wall by Stepped Frequency Continuous Wave Radar in Ultra-Wideband Range[J].IET Radar,Sonar&Navigation,2011,5(4):416-425.

[12]Tivive F H C,Amin M G,Bouzerdoum A.Wall Clutter Mitigation Based on Eigen-Analysis in Through-the-Wall Radar Imaging[C]∥17th International Conference on Digital Signal Processing,Corfu,Greece:[s.n.],2011:1-8.

[13]Riaz M M,Ghafoor A.Principle Component Analysis and Fuzzy Logic Based Through Wall Image Enhancement[C]∥Progress In Electromagnetics Research,[s.l.]:[s.n.],2012:461-478.

[14]Riaz M M,Ghafoor A.Fuzzy Logic and Singular Value Decomposition Based Through Wall Image Enhancement[J].Radio Engineering,2012,21(2):580-589.

[15]Tivive F H C,Bouzerdoum A,Amin M G.An SVDBased Approach for Mitigating Wall Reflections in Through-the-Wall Radar Imaging[C]∥IEEE Radar Conference,Kansas City,MO:[s.n.],2011:519-524.