基于拉普拉斯金字塔变换的小波域图像融合

黄小丹

(西安电子科技大学CAD 研究所，陕西 西安 710071)

由于各种成像传感器工作于不同的波长范围，有不同的工作环境和要求，所以，在复杂的实际应用中，单一传感器图像数据往往不能提供足够的信息。例如可见光图像对比度较高，对细节显示较为清晰，但在黑暗背景中却不易观察到目标，而红外图像则相反，能显示出目标的大致轮廓但却缺乏图像的细节信息。图像融合技术即是综合和提取两个或多个多源图像的信息，以获得对同一场景或目标更为准确、全面和可靠的图像，使之更加适合于人眼感知或计算机后续处理［1］。

近年来，人们提出了多种图像融合方法［2－6］，其中基于多分辨率分解［7］的图像融合方法是研究内容之一。自从1984 年Burt 将拉普拉斯金字塔变换方法引入图像融合领域后，各种基于金字塔变换的融合方法便不断涌现。金字塔变换融合方法在可见光图像和红外图像融合中展现了良好的融合效果，但在多聚焦图像融合中却不够理想，而基于小波变换的融合方法在可见光图像和红外图像融合中效果不佳，却在多聚焦图像融合中要优于金字塔变换法［8－10］。本文将两种方法有机结合，提出基于拉普拉斯金字塔变换的小波域图像融合方法，实验结果表明，该方法成功克服了上述问题，在可见光图像和红外图像融合、多聚焦图像融合以及局部模糊图像融合中均表现出了理想的效果，且优于平均融合法、梯度金字塔融合法、FSD 金字塔融合法、平移不变离散小波变换融合法等常用的融合方法［3－6］。

1 图像小波变换和图像金字塔变换

图像融合中的小波变换和金字塔变换都属于多分辨率分解方法的范畴，其基本思想是根据相应算法将源图像分解到具有不同空间分辨率和频率特性的子带当中，在不同分解层不同频带上分别融合，最后逆变换得到最终的融合图像。

1.1 图像小波变换

在实际应用中，尤其是在计算机上进行图像处理时，一般使用离散小波变换，离散小波变换是对连续小波变换在连续的尺度参数和连续平移参数加以离散化得到的，减少了小波变换的冗余度。

Mallat 提出了信号的塔式多分辨率分析与重构的快速算法称为Mallat 算法［7］，它是一种实现离散小波变换的高效计算方法，即利用两个一维滤波器来实现对图像的二维小波分解及重构。若设G、H 分别为高通滤波器和低通滤波器，首先在水平方向上分别用G和H 对图像I(x，y)滤波，并进行列下采样得到IH(x，y)和IG(x，y)，接着继续对IH(x，y)、IG(x，y)在竖直方向上滤波，并进行行下采样，可得到同一分解层的4 幅子图像ILL(x，y)、ILH(x，y)、IHL(x，y)和IHH(x，y)。将ILL(x，y)作为原图像继续上述过程，即可得到图像I(x，y)更高层次的多层小波分解。此过程中，ILL(x，y)是原图像I(x，y)的多分辨率低频分量，即I(x，y)的近似图像;ILH(x，y)、IHL(x，y)和IHH(x，y)分别为原图像在I(x，y)水平、竖直和对角方向上的细节子图像。Mallat 算法的逆过程即是上述分解过程的反过程。

Mallat 算法在尺度j－1 上的实现用公式可描述如下

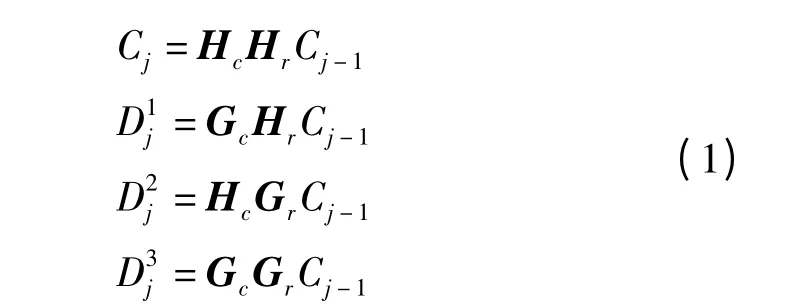
其中，H*和G*分别为H 和G 的共轭转置矩阵。

1.2 图像拉普拉斯金字塔变换

图像的拉普拉斯金字塔变换是从高斯金字塔的基础上演变来的，所以首先得对图像进行高斯金字塔变换。图像的高斯金字塔是通过利用一个具有低通特性的窗口函数w 对底层图像进行卷积，再对卷积结果进行隔行隔列降采样实现的。设Gk表示图像I 的第k层高斯金字塔，则原图像作为第0 层G0=I，其第k 层可表示为Gk=［ω×Gk－1］↓2，k=1，…，N，其中［］↓2表示对该层进行隔行隔列下采样。由此可得第k 层拉普拉斯金字塔Lk为

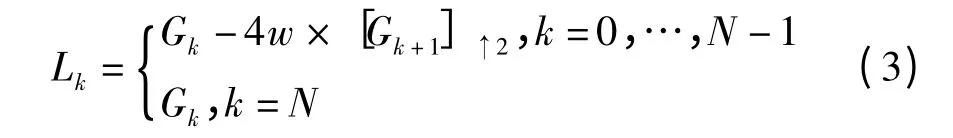
2 小波域图像融合方法(LAP－WT)

金字塔变换融合方法减少了高斯金字塔中大量的冗余信息，但忽略了分解层之间系数的相关性。小波变换法具有良好的空域和频域的局域性，可以较好地保留多聚焦图像的高频信息，仍在一定程度上会丢失原始图像中的一些边缘信息［8］，本文提出的将拉普拉斯金字塔法和小波变换方法相结合的图像融合方法，克服了单一方法只适应某一类图像融合的缺陷，在可见光图像与红外图像的融合、多聚焦图像融合以及局部模糊图像融合等应用中都取得较为理想的效果。这里在运用拉普拉斯金字塔变换的融合方法中，采用对变换中的低频部分使用平均值、高频部分取较大值的融合规则，而小波变换中则选用了db4 小波变换法。图1 是两幅待融合图像一层小波分解后，用LAP－WT融合过程示意图。

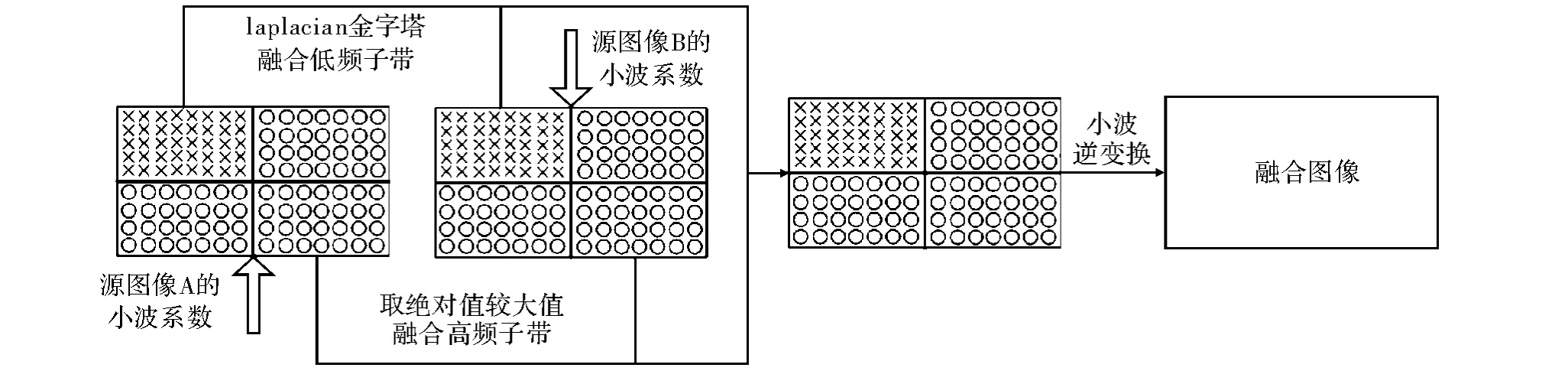
图1 LAP－WT 一层小波系数融合过程示意图

图1 中，“×”表示低频子带，“○”是高频子带。

(2)用拉普拉斯金字塔法融合CaN和CbN，结果记为CfN，即融合图像第N 层的小波低频子带。

(3)对第j 层中3 个高频子带选用取绝对值较大者的融合规则即

(5)重复步骤(3)和步骤(4)，直到得到最终的融合图像F。

3 实验过程及结果分析

如图2 ～图4 所示是本实验涉及的3 组不同成像机制的待融合源图像，其中图2(a)和图2(b)分别为同一场景的可见光图像和红外图像，分辨率为360×270;图3(a)和图3(b)分别为同一场景不同聚焦图像，分辨率为512×512;图4(a)和图4(b)分别为同一场景不同局部模糊图像，分辨率为480×720，这组图是将完全清晰的图像用半径为5 的圆形区域均值滤波器处理得到的。

图2 同一场景的红外和可见源图像

图3 同一场景的不同聚焦图像

图4 局部模糊图像

在实现LAP－WT 中，对图像进行两层小波分解即N=2，最高层低频子带融合采用了3 层拉普拉斯金字塔变换。

为充分验证本文提出的融合方法，选用了多种融合方法与之作比较。5 种基于金字塔变换的融合方法:拉普拉斯金字塔变换融合方法(LAP)、FSD 金字塔变换融合方法(FSDP)、梯度金字塔变换融合方法(GRAP)、对比度金字塔变换融合方法(RATP)、形态学差异金字塔变换融合方法(MODP);一种基于小波变换的融合方法:选用db4 小波对图像进行小波分解，采用对低频子带融合取平均值而对高频子带取绝对值较大者的融合规则进行融合，此融合方法简记为WT;还有基于层次主分量分析融合法(HPCA)［8］和平均融合法(AVR)。

为进行有针对性的对比，WT 也进行两层小波分解，低频部分取平均值、高频部分取绝对值较大值进行融合;5 种金字塔变换融合方法进行3 层分解，低频部分取平均值、高频部分取较大值进行融合。

另外，还采用6 种常用的客观图像融合质量评估方法，以达到从多种不同角度对不同机制的融合图像进行全方面评定的目的。这6 种质量评估方法分别为:Xydeas 和Petrovic'提出的客观评价方法(Q)、熵(EN)、标准偏差(SD)、结构相似度(SSIM)、峰值信噪比(PSNR)和交叉熵(CE)。表1、表2 和表3 以文中所用的三组源图像为例，给出了用客观图像质量评估方法度量各种图像融合方法的计算结果。

表1 可见光图像和红外图像的融合质量评估

表2 不同聚焦图像的融合质量评估

表3 局部模糊图像的融合质量评估

由于各种图像质量评估方法定义的不同，在所选的6 种评估方法中，交叉熵CE 的计算值越小说明该图像的融合效果越好，而相反的，其他5 种评估方法计算值越大表明相应的图像融合质量越好。为便于观察，表1 ～表3 中将根据图像质量评估方法得到的较好的图像融合结果用粗体进行标示。由此，根据以上实验数据，也可以看出LAP－WT 融合效果最好，LAP次之，其他融合方法的融合效果均不理想。比如平均融合方法AVR 可能是由于选取灰度平均值融合，使融合图像损失了一定的纹理信息，图像清晰度降低;WT在各组图像融合中的表现都相对较为一般，不尽如人意，这可能是由于小波分解层数太少，图像各方向信息没有被准确充分利用;LAP 对不同聚焦图像及局部模糊图像具有良好效果，但对红外图像的融合结果则不够理想;而本文提出的LAP－WT，其一方面具有小波变换的优点较好地保留了的高频信息，另一方面结合金字塔变换继承了源图像中的一些低频信息，在实验中均表现出了良好的融合效果，包含的信息量最大，从源图像继承的信息最多，融合效果最好。

4 结束语

本文将拉普拉斯金字塔变换融合方法和小波变换融合方法相结合，提出了基于拉普拉斯变换的小波域融合方法，该方法采用对小波分解最高层的低频子带用拉普拉斯金字塔变换方法融合、对各层高频子带取绝对值最大值的融合规则完成图像融合。实验结果显示，该方法对小波分解的层数要求不高，计算量小，与多种常用融合方法相比，在多种类型图像融合中均表现出了优越性。

［1］ 杨翠，张建奇.基于红外特征与区域相似的图像融合算法［J］.西安电子科技大学学报，2006，33(6):871－875.

［2］ PATIL U，MUDENGUDI U.Image fusion using hierarchical PCA［C］.Himachal Pradesh:Proceedings of the 2011 International Conference on Image Information Processing，2011.

［3］ TOET A.Image fusion by a ratio of low pass pyramid［J］.Pattern Recognition Letters，1989，9(4):245－253.

［4］ ROCKINGER O.Image sequence fusion using a shift－invariant wavelet transform［C］.Proceedings of IEEE International Conference on Image Processing，1997:288－291.

［5］ 严春满，郭宝龙，杨秀红.一种抗噪声的高效多聚焦图像融合算法［J］.西安电子科技大学学报，2011，38(3):63－68.

［6］ 梁栋，李瑶，沈敏，等.一种基于小波－Contourlet 变换的多聚焦图像融合算法［J］.电子学报，2007，35(2):320－322.

［7］ MALLAT S G.A theory for multi－resolution signal decomposition:the wavelet representation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1989，11(7):674－693.

［8］ 阮涛，那彦，王澍.基于压缩感知的遥感图像融合方法［J］.电子科技，2012，26(4):43－46.

［9］ 杨莎莎，田小平，吴成茂.基于小波变换的多聚焦图像自适应融合［J］.西安邮电学院学报，2012(3):24－29.

［10］杨萱，杨万海，裴继红.基于小波分解的不同聚焦图像融合方法［J］.电子学报，2001，29(6):846－848.