OFDM 电力线通信系统的时域信道估计方法
查佳佳,邵汉钦,王荣军
(南京航空航天大学 电子信息工程学院,江苏 南京 210016)
电力线通信是一种以电力线为媒介传输数据信号的通信方式,其无需铺设额外的线路,大幅降低了通信成本。但由于电网的分支结构和节点处阻抗不匹配,使得电力线通信信道具有显著的多径特性[1],而正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)技术可有效克服信道多径时延,且频谱利用率高,适用于电力线通信系统。基于OFDM 的G3-PLC(Power Line Communication)是一个国际主流的窄带电力线通信协议[2],其支持智能电表管理、照明控制、电动车智能充电等应用。为降低由多径传播引起的频率选择性衰落,G3-PLC 系统利用前导序列估计信道特性,从而进行频域均衡,抵消了信道多径所引起的码间干扰,本文主要研究了G3-PLC 系统的信道估计方法。
基于OFDM 系统的信道估计方法众多,G3-PLC利用前导序列估计信道信息,通常可采用传统的LS(Least Squares)、LMMSE(Linear Minimum Mean Square Error)算法,或基于DFT(Discrete Fourier Transform)变换的估计算法。LS 算法简单,但在低信噪比时性能不理想。LMMSE 算法具有良好的性能,但统计信道相关性和矩阵求逆的复杂度较高,通常采用奇异值分解(Singular Value Decomposition,SVD)降低求逆复杂度[3]。基于变换域的DFT 算法将LS 频域估计值变换到时域,通过时域置零实现降噪,该算法复杂度低于LMMSE 算法,但其性能对阈值的选取较为敏感[4]。
本文针对G3-PLC 系统,通过预置电力线信道最大时延估计其时域特性,具有降噪效果,但相应的时频变换矩阵不满秩[5],无法求逆。在预置最大信道时延后,Simeone[5]提出采用子空间跟踪算法迭代获得时延空间正交基,将传统LS 频域估计值在子空间上投影,达到信噪分离的效果,该方法需要多次矩阵相乘,实现复杂度较高。本文通过修正变换矩阵,解决了采用LS准则存在的矩阵不可逆问题,并取得了良好的性能。同时进一步提出一种无需信道统计特性的时域LMMSE 算法,大幅降低了复杂度。仿真结果表明,两种改进算法复杂度均较低,性能良好,对系统实现具有参考意义。
1 系统模型
1.1 电力线信道
目前的文献中,窄带电力线通信的信道模型尚未形成统一标准。根据Zimmermann[6]提出的电力线信道多径模型,其传递函数可表示为
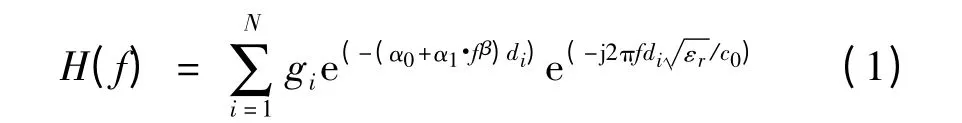
其中,N 为路径总数;gi、di表示路径i 的加权系数和长度;α0、α1表示衰减参数,由传输线特性决定;β 是指数衰减因子,通常介于0.5 ~1 之间;εr是电力线介电常数;c0表示光速。
本文在进行系统算法仿真中,即采用了上述信道模型,并叠加以高斯白噪声。
1.2 G3-PLC 系统
G3-PLC[7]采用OFDM 调制技术,图1 为系统物理层收发框图。系统采样率为400 kHz,FFT 点数为256,支持35.9 ~90.6 kHz 频段通信,对应256 个载波中36 个子载波(编号23 ~58)。G3-PLC 的前导序列由8 个SYNCP 符号和1.5 个SYNCM 符号组成,系统利用以上9.5 个OFDM 符号进行信道估计。

图1 G3-PLC 物理层收发框图
在G3-PLC 中,已知36 个幅值相同、相位各异的调制信息P(k),23≤k≤58,经系统OFDM 调制得训练序列p(n),0≤n≤255。p(n)和-p(n)分别对应前导的SYNP、SYNM 符号。训练序列p(n)经过信道,接收端FFT 解调,得到OFDM 符号Y(k)

2 信道估计算法
2.1 算法分析
设H(k)对应有限长时域冲激响应h(n),两者关系为
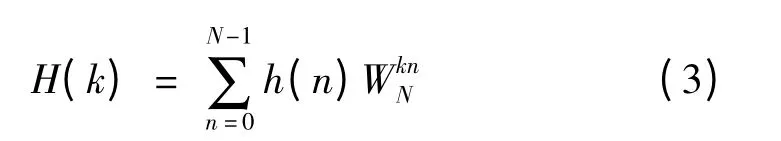
假设信道最大时延为L,则上式用向量表示为

其中,HK对应K 个可用子载波;Fsub表示变换矩阵



上式即预置时延后的时频变换关系。相对于系统的时间分辨率,这种时延间隔过于紧密,导致Fsub不满秩[5],是一个病态系数阵,无法直接应用LS 准则估计时域h。
2.2 修正的时域LS 算法
为有效应用LS 准则,本文采取了修正变换矩阵Fsub的方法。设Fsub的奇异值分解形式为

其中,U1和V1是K×K 和(L+1)×(L+1)的酉矩阵,不妨设K≥L+1,则
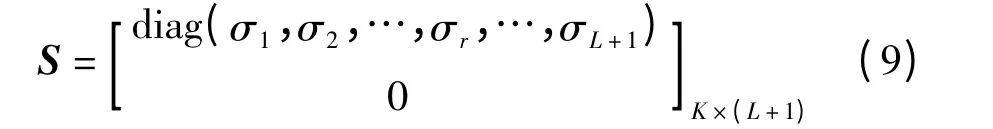
其中,σ1≥σ2≥…≥σr≥σL+1>0,因Fsub呈病态,奇异阵S 包含若干接近于零的奇异值σi。当σi较小时,直接采用LS 准则的均方误差将较大,虽不是无偏的,但并非为最优解[8]。本文采用截断奇异值法[8],设置截断参数T,将<T 的奇异值直接用0 代替,得修正的奇异阵Sr

其中,σr满足≥T。相关文献给出了L 曲线法、极小化均方误差法等计算T,这里Fsub确定,可通过仿真分析选取最优截断参数T。
综上,经过修正,相应的时域估计值为

进一步将时域估计值变换到频域,即

将式(8)和式(11)代入上式可化解得

其中,Ir×r表示r 阶单位阵具有共轭对称性。
这种修正的时域LS 算法中,Fsub由可用子载波k的分布和信道最大时延L 确定,所以实际可预先计算出矩阵系数存储在本地,所需存储空间为接收端先计算出频域LS 估计值,再和本地矩阵相乘,即得算法改进值,其中包含K2次复乘,K2-K 次复加运算,其复杂度较低。
2.3 简化的时域LMMSE 算法
为进一步提高估计性能,对式采用LMMSE 准则估计h
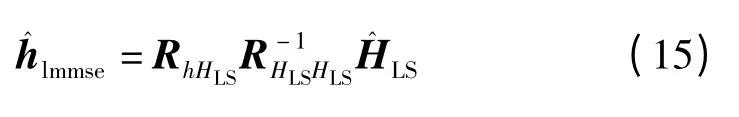
其中
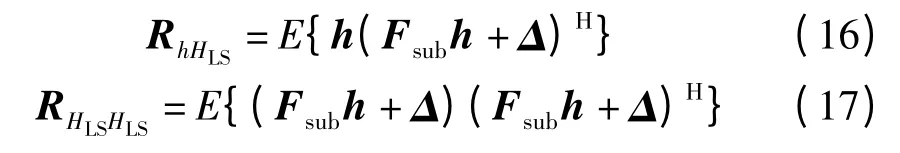
整理得

其中,Rhh表示信道时域自相关阵。实际中,统计Rhh和矩阵求逆的复杂度均较高。
假设各径相互独立,则Rhh为对角阵。而本文将Rhh设为单位阵,则上式可简化为
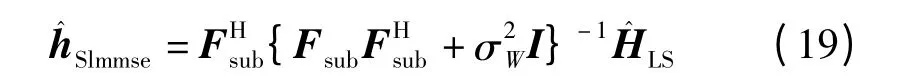
当调制子载波等间距时,FsubFHsub为共轭对称的Toeplitz矩阵,可采用Levinson-Durbin 递归算法降低矩阵求逆的复杂度。这里采用SVD[3]进一步化解,则有

其中,U2是酉矩阵;Λ 为对角阵,对角元素满足λ1≥λ2≥…≥λK。
综上,简化的信道时域估计值可化解为

进一步将时域估计值变换到频域,并化解

图2 是该改进算法的实现流程图。这种简化的时域LMMSE 算法,将时域自相关阵简化为单位阵,即在信道统计特性未知的情况下,假定各径统计均匀分布。根据图2 流程,简化算法包含2K2+K 次复乘,2K2-2K 次复加运算。传统的LMMSE 算法,不考虑计算信道二次相关性的复杂度,仅矩阵求逆复杂度为o(K3)。因此相比之下,简化算法复杂度大幅降低。
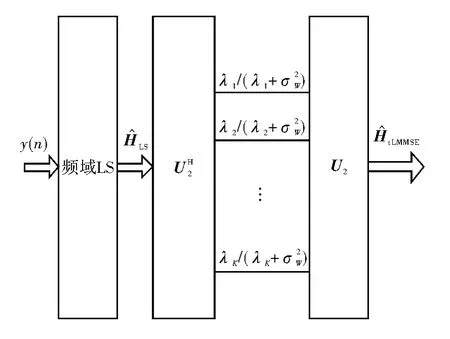
图2 简化的时域LMMSE 算法流程
3 仿真结果及分析
针对G3-PLC 系统,仿真中采用BPSK 调制,假设信道最大时延L 为22 个采样点。为了最优化修正时域LS 算法,在不同截断参数T 下,对系统均方误差(MSE,Mean Square Error)性能进行了仿真对比,如图3所示。比较各曲线,当T=1 时,修正算法性能总优于T <1;当T >1 时,低信噪比时性能较好,但在高信噪比时性能变差。综合整体性能与稳定性分析,选取T=1 作为修正算法的最优截断参数。

图3 修正时域LS 算法下不同T 的MSE 性能比较
基于以上条件,将改进算法和传统的频域LS 算法、LMMSE 算法、DFT 算法进行了性能对比,包括MSE和BER(Bit Error Rate)性能,仿真结果如图4 和图5所示。其中,LMMSE 算法的协方差矩阵由真实的H(f)计算,仿真得到理想LMMSE 值。而基于变换域的DFT 算法,仿真中截取时域两端窗长为最大时延的3/4和1/4,中间补零[9]。
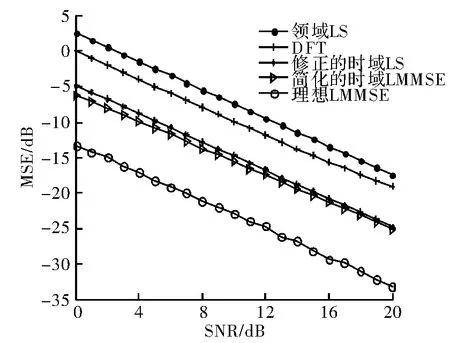
图4 不同算法下MSE 性能

图5 不同算法下BER 性能比较
图4 表示各算法的MSE 性能,传统的频域LS 算法性能最差,DFT 算法性能介于LS 和LMMSE 算法之间。由图4 可看出,通过预置信道时延,修正的时域LS 算法相比频域LS 算法性能提高了7 dB。对于G3-PLC 系统,可用子载波数K 为36,所以修正算法只要额外1 296 次复乘,1 260 次复加,即可求得改进值,从而在较低的复杂度下大幅提高了估计性能。对于简化的LMMSE 算法,算法复杂度为2 628 次复乘,2 520 次复加,而传统LMMSE 算法复杂度为46 656 次复乘。根据图4 所示,相比理想LMMSE 估计值,由于信道二次相关性被简化近似,简化算法仍存在一定的性能损失,但复杂度大幅降低。进一步,对比两种改进算法,由于简化算法中考虑了噪声的影响,所以其性能优于修正的时域LS 算法,特别在低信噪比时,MSE 性能提高1 ~2 dB。
图5 给出了G3-PLC 系统下,不同信道估计算法的BER 性能。相比传统的频域LS 算法,修正的时域LS算法性能提升约3 dB,而简化算法与理想LMMSE 算法之间的差距<1 dB。仿真表明,两种改进算法性能良好。
4 结束语
本文基于G3-PLC 系统,根据PLC 信道的有限时延特性,提出了修正的时域LS 算法,有效地解决了矩阵不可逆问题。而简化的时域LMMSE 算法,则避免了求解信道统计特性的复杂度。仿真结果表明,这两种改进的时域信道估计算法,在较低的复杂度下,具有良好的性能和稳定性。同时,改进算法也可适用于其他OFDM 系统。
[1] FRANCISCO J C,JOSE A C,LUIS D,et al.A channel model proposal for indoor power line communications[J].IEEE Communications Magazine,2011,49(12):166-174.
[2] RAZAZIAN K,UMARI M,KAMALIZAD A,et al.G3-PLC specification for powerline communication:Overview,system simulation and field trial results[C].2010 IEEE International Symposium on Power Line Communications and Its Applications,2010,3:313-318.
[3] OVE E,MAGNUS S,JAN-JAAP B,et al.OFDM channel estimation by singular value decomposition[J].IEEE Transactions on Communications,1998,46(7):931-939.
[4] LEE Y S,SHIN H C,KIM H N.Channel estimation based on a time-domain threshold for OFDM systems[J].IEEE Transactions on Broadcasting,2009,55(3):656-662.
[5] SIMEONE O,BAR-NESS Y,SPAGNOLINI U.Pilot-based channel estimation for OFDM systems by tracking the delay-subspace[J].IEEE Transactions on Wireless Communications,2004,3(1):315-325.
[6] ZIMMERMANN M,DOSTERT K.A multipath model for the powerline channel[J].IEEE Transactions on Communications,2002,50(4):553-559.
[7] Electricite Reseau Distribution France(ERDF).PLC G3 physical layer specification[S].Paris:Électricité Réseau Distribution France,2009.
[8] 张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004.
[9] HOU X L,ZHOU E,CHEN J P,et al.Robust channel estimator for MIMO-OFDM systems with FPGA implementation[C].APCC 14th Asia-Pacific Conference on Communications,2008,10:1-5.

