基于FPGA 的可配置FFT IP 核实现研究
李大习
(江苏自动化研究所 计算机事业部,江苏 连云港 222061)
在现代声纳、雷达、通信、图像处理等领域中,数字信号处理系统经常要进行高速、高精度的FFT 运算。现场可编程逻辑阵列(FPGA)是一种可定制集成电路,具有面向数字信号处理算法的物理结构。用FPGA实现FFT 处理器具有硬件系统简单、功耗低的优点,同时具有开发时间较短、成本较低的优势。基于FPGA实现的数字信号处理系统具有较高的实时性和嵌入性,并能方便地实现系统集成与功能扩展[1]。基于FPGA 的硬件实现FFT 通常有两种方法:(1)并行方法,其采用多个蝶形处理器并行运算,能对较高的数据采样率进行运算,但其硬件规模较大,当在FPGA 上要实现较大点数的FFT 时较为困难。(2)串行方法,采用一个蝶形处理器完成运算,使用的逻辑资源较少,但运算速度较慢[2]。本文在串行方法的基础上实现了一种在FPGA 上实现的可配置FFT IP 核,具有输入点数可配置(实现0 ~4 096 点自由配置)、数据位宽可配置、分解基可配置的特性。
1 原理分析
自从基2 快速算法出现以来,人们仍在不断寻求更快的算法。基4 FFT 算法比最初的基2 FFT 算法更快,但从理论上讲,用较大的基数还可进一步减少运算次数,但要以程序(或硬件)变得更复杂为代价[3]。提高FFT 处理速度的4 个主要技术途径是采用流水线结构、并行运算、增加蝶形处理单元数目和高基数结构[4]。
1.1 基2 算法基本原理
点数N 是2 的整数次幂,将x(n)先按n 的奇偶分成两组
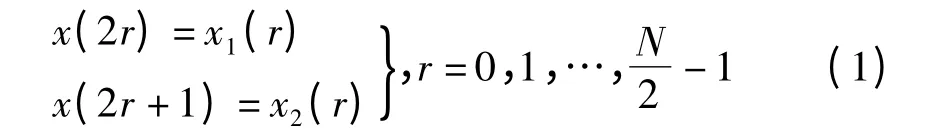
则可将DFT 化为

1.2 基4 算法基本原理
与基2 算法类似,对于N 点有限长序列x(n)的DFT 按照时域分解展开有[5]

对式(3)进行变量替换得到
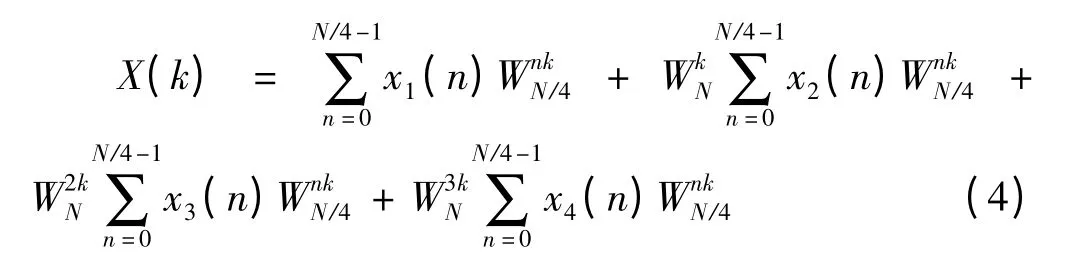
2 可配置FFT IP 核硬件结构
现有的FFT IP 核在硬件实现时不具备并行度可配置能力,只提供全循环、全流水、循环展开与流水结合等形式下的某种特定实现[6],可重用性较差,难以适应不同的计算吞吐量和对计算资源和计算时间的需求[7-8]。可配置FFT IP 核技术实现FFT 算法流水、循环等并行化参数的可配置问题,兼顾FFT 转换点数、输入输出数据位宽、蝶形运算基数、输入输出FIFO 深度的可配置,满足不同应用条件下IP 复用的需求,适应各种环境和数据吞吐量的FFT 运算[9]。可配置FFT IP 核功能组成如图1 所示。
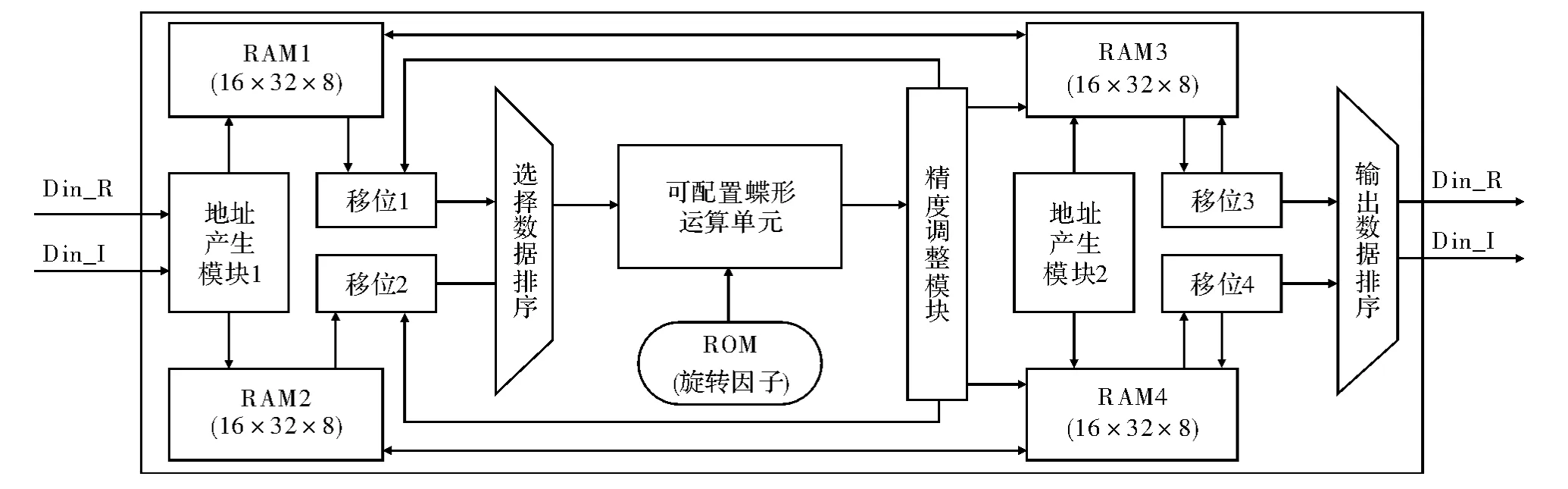
图1 FFT 算法IP 核功能组成
如图1 所示,该IP 主要包括RAM、ROM、地址产生模块、移位模块、选择数据排序模块、可配置蝶形运算单元、精度调整模块和输出数据排序模块,Din_R 和Din_I 是FFT 输入数据的实部和虚部,Dout_R 和Dout_I 是FFT 变换结果的实部和虚部。RAM1 和RAM2 存储了FFT 迭代过程中的输入数据,RAM3 和RAM4 存储了FFT 迭代过程中的计算结果,RAM1 和RAM2、RAM3 和RAM4 均为乒乓结构。地址产生模块主要产生向RAM 写入数据和从RAM 读出数据的地址。ROM 中存储了FFT 需要的旋转因子。
2.1 IP 核整体方案
设计可配置FFT 处理,其整体结构如图2 所示,设计采用基2 蝶形和基4 蝶形运算两种配置方式,供用户选择。输入数据实部和虚部分开存储,需4 个RAM,为实现对连续流输入可连续流输出,其模块构成如图2 所示。

图2 FFT IP 核构成图
如图2 所示,外部输入数据的实数部分Din_R、虚数部分Din_I,以及输入数据的地址信号ADR,首先进入RAM_ADDR 单元,选择合适的时钟周期将不同点数的原始数据送入RAM 单元,当输入数据的实数和虚数以及其地址准备好的时候,RDY 输出1。BIT_SFT单元完成输入数据地址的移位变换,实现奇偶分离。当数据地址准备好时,RDY 输出1,当RAM_ADDR 或BIT_SFT 这两个单元中的一个单元准备好时,便可触发RAM 单元,将外部数据写入到RAM 的指定地址。RAM 中的数据符合可配置点数要求后,进入NUM_IN单元,其中输出的数据DOR/DOI 就是符合基2 蝶形或基4 蝶形运算的数据顺序。这些原始数据进入蝶形运算单元BUTTERFLY,蝶形单元通过U_SELECT 单元选择蝶形运算的分解基,实现基2 蝶形运算、基4 蝶形运算的可配置功能。其中R4_FFT 是基4 蝶形运算单元,R2_FFT 是基2 蝶形运算单元,蝶形运算过程中所需的旋转因子存储在ROM_RAT 单元中,根据选择不同分解基的蝶形运算,BUTTERFLY 单元产生相应的地址,选择其计算过程中的旋转因子。当蝶形运算完成后,结果数据进入U_CNORM 单元,进行顺序调整和精度处理;其中PR 信号是用户指定的精度信号,PR[1∶0]可提供3 种精度,OVF 信号是数据溢出信号,若置1 表明FFT 结果数据超出了表示范围,则要按照截位处理以保证数据准确。当数据输入完成后,结果数据进入NUM_OUT 单元,由于DIT 算法输出结果以倒序形式输出,所有需要NUM_OUT 进行地址调整,FFT 变换结束后的结果实数部分Dout_R,虚数部分是Dout_I,地址信号是R_ADDR,以正确的顺序和形式输出。
2.2 可配置蝶形单元模块
在FFT IP 核的蝶形运算单元设计中,蝶形单元的运算过程:第一个时钟周期是将下结点与旋转因子复乘的实数乘法进行计算;第二个时钟周期是将复乘中的实数进行加减运算;在第三个时钟周期是计算复乘结果与上结点的加减运算,即将蝶形运算单元的结果输出。可配置蝶形运算通过在基2 和基4 两种分解基之间切换来实现,其模块图如图3 所示。

图3 可配置蝶形运算模块图
如图3 所示,数据输入时能信号EN 信号置1,则整个蝶形运算单元的数据输入模块NUM_IN、旋转因子模块ROM_RAT、分解基选择模块U_SELECT 进入使能状态;START 信号置1,则分解基选择单元U_SELECT 模块开始进入状态机。根据用户设置,如果选择基2 算法蝶形运算单元,则将输入数据的实部和虚部送入R2_FFT 模块;如果选择基4 算法蝶形运算单元,则将输入数据的实部和虚部送入R4_FFT 模块;如果选择混合基,则需要在状态机中加入判断条件,准确控制分支。当蝶形运算完成时,FFT 运算结果数据的实数部分Dout_R[nb+2∶0],虚数部分Dout_I[nb+2∶0]比输入数据的位数[nb∶0]扩展了3 位,用于精度调整模块进行精度控制。
蝶形运算的旋转因子存储在ROM_RAT 中,其中存储了基4 运算和基2 运算的旋转因子,实部和虚部分开存储,通过外部信号EN 对其使能,为控制ROM存储空间的占用,不同分解基的旋转因子可公用,通过地址信号ADR 选取控制。
3 仿真、综合结果分析与验证
将设计的IP 核进行基于ModelSim 的仿真,设置时钟频率为200 MHz,数据位宽为36 位,在基2 和基4两种分解基下,分析1 024 点和4 096 点的运算效率,其仿真图像如下所示。
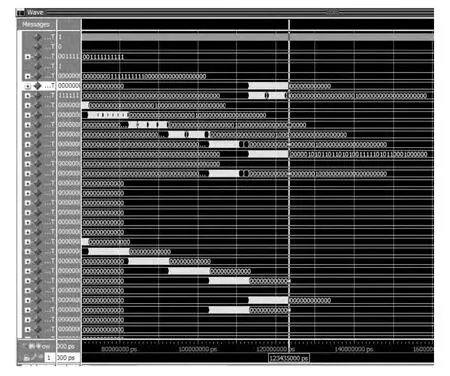
图4 200 MHz 1 024 点基2FFT 运算仿真结果

图5 200 MHz 1 024 点基4FFT 运算仿真结果
图4 是1 024 点的基2 算法仿真结果,在这种算法下完成数据录入的时间点为113.1 μs,完成结果输出的时间点为123.4 μs,运算时间为10.3 μs。图5 是1 024点的基4 算法仿真结果,在该种算法下完成数据录入的时间点51.3 μs,完成结果输出的时间点是61.6 μs,运算时间为8.3 μs。
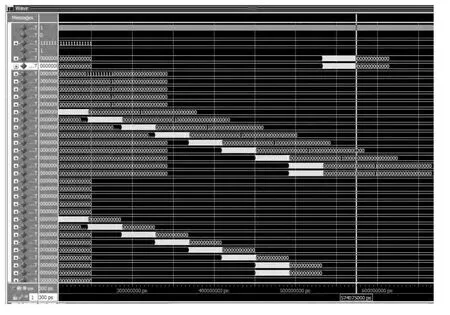
图6 200 MHz 4 096 点基2FFT 运算仿真结果
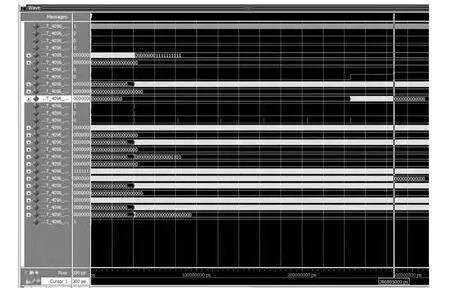
图7 200 MHz 4 096 点基4FFT 运算仿真结果
图6 是4 096 点的基2 算法仿真结果,在这种算法下完成数据录入的时间点533.1 μs,完成结果输出的时间点是574.1 μs,运算时间为40 μs。图7 是4096点的基4 算法仿真结果,在该种算法下完成数据录入的时间点为245.7 μs,完成结果输出的时间点是286.9 μs,运算时间为41.2 μs。
板级验证选用Xilinx 公司的Virtex-5 xc5vfx70t器件进行综合、布局布线和时序分析。将得到的数据与其他设计实现进行比较,其消耗的资源,以及在200 MHz 时钟情况下不同点数的FFT 处理器进行一次处理需要的时间,与文献[10]换算后得到的数值对比如表1 所示。
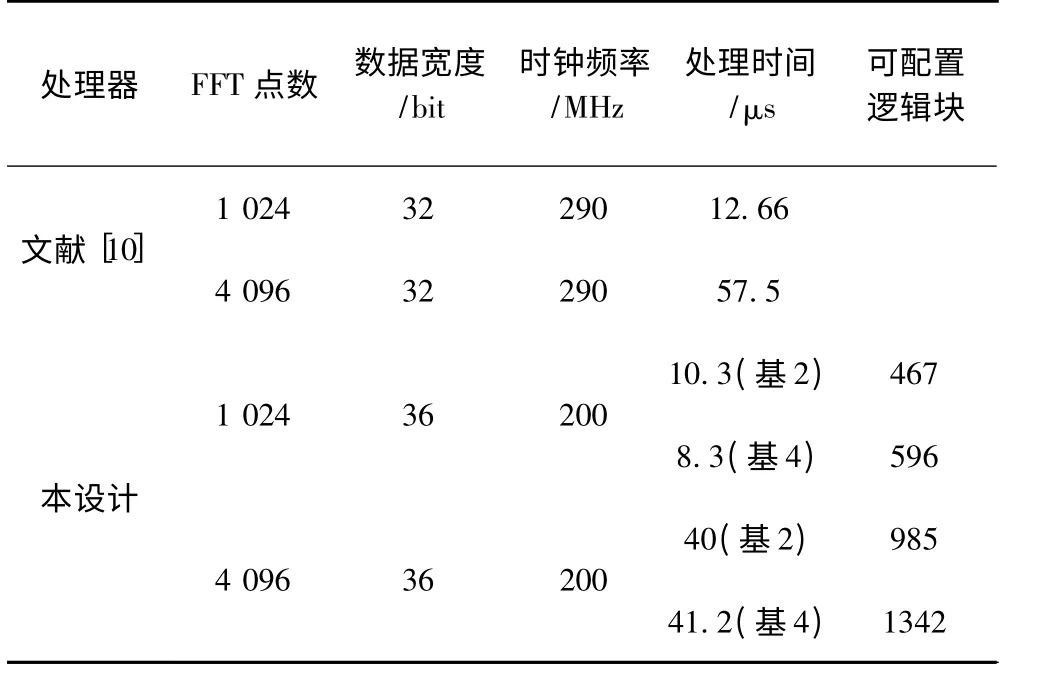
表1 FFT 运算效率比较
4 结束语
本文设计的可配置FFT IP 核具有灵活性强、容易扩展和设计可复用的特点,实现分解基可配置、位宽可配置、输入输出点数可配置。从验证结果可以看出,本文数据的可配置IP 核具有结构简单及占用硬件资源适当的特点,在FPGA 中以实现高速数字信号处理,在处理速度和灵活性方面更有优势。随着处理点数的增加,其优越性将更加明显。
[1] 张燕燕,洪龙.Windows 环境下FFT 多核并行算法的设计实现[J].计算机技术与发展,2010(9):74-77.
[2] 胡广书.数字信号处理[M].北京:清华大学出版社,2003.
[3] 肖江,胡柯良,邓元勇.基于CUDA 的矩阵乘法和FFT 性能测试[J].计算机工程,2009,35(10):7-10.
[4] 张犁,李双飞,石光明,等.一种FFT 并行处理机的设计与实现[J].西安电子科技大学学报:自然科学版,2010,37(4):630-635.
[5] 李仕专,李维涛,姜全贤,等.一种基于并行计算的快速FFT IP 核设计[J].计算机与数字工程,2010,38(4):139-141.
[6] 万红星,陈禾,韩月秋.一种高速并行FFT 处理器的VLSI结构设计[J].电子技术应用,2004(12):45-48.
[7] GHISSONI S,COSTA E,MONTEIRO J,et al.Combination of constant matrix multiplication and gate-level approaches for area and power efficient hybrid radix-2 dit/fft realization[C].2011 18th IEEE International Conference on Electronics,Circuits and Systems(ICECS),2011:567-570.
[8] MATEUS B F,EDUARDO A,César da Costa,et al.Martins design of power efficient butterflies from Radix-2 DIT FFT using adder compressors with a new XOR gate topology[J].Analog Integrated Circuits and Signal Processing,2012,73(3):945-954.
[9] 李欣,刘峰,龙腾.定点FFT 在TS201 上的高效实现[J].北京理工大学学报,2010,30(1):88-91.
[10]齐华,李勇,郝重阳.一种块递推实时FFT 算法模块设计与实现[J].西北工业大学学报,2009,27(2):240-244.

