慢速目标仅测角无源定位算法研究

张 凯,刘 洋

(1.海军92941部队93分队,辽宁葫芦岛125001;2.国防科技大学电子科学与工程学院,湖南长沙410073)

0 引言

相对雷达等有源探测手段,无源定位系统具有不发射电磁信号、生存能力强及作用距离远等显著优点[1]。单站无源定位技术作为反辐射导弹核心技术之一,原理就是利用单个运动的观测站对辐射源进行连续测量,在积累一定信息量基础上,用多个定位曲线(面)的交会实现定位。其中仅测角定位问题仍然是单站无源定位中非常活跃的研究领域。

慢速运动目标仅测角定位的难点在于：定位时完全忽略目标速度,会对定位带来误差;定位时将慢速目标看作匀速运动目标建模,定位缺乏可观测性,定位跟踪无法收敛[2]。对于单观测站无源定位,文献[3]给出了仅测角定位法的可观测性分析,指出观测器机动可以提高定位的可观测性。本文研究的反辐射导弹运动形式固定,助推段一般会急剧加速直线飞行,助推段结束后,一般会等速等高飞行,但中段制导是沿着方案弹道飞行,加速、减速是不太现实的,转弯则需要在可用法向过载的基础上实现。

文献[4]考虑了在增加不同观测量,研究系统的可观测性,实现观测器无机动条件下对匀速运动目标的无源定位方法,但增加观测量有可能要改变导弹的设计,对反辐射导弹不一定适用。因此,是否增加观测量主要还是考虑反辐射导弹被动导引头自身的测量设备等条件,也即现有的反辐射导弹被动导引头的测量条件。而目前大多数反辐射导弹都采用了仅测角体制,因此本文考虑在仅测角条件下,观测平台无机动实现对慢速目标的定位。

综上所述,分析速度对定位误差的影响以及是否满足末制导雷达对定位精度的需求,是解决慢速运动目标定位的首要工作。

1 慢速目标定位模型及误差分析

1.1 慢速目标定位模型

反辐射导弹中段制导阶段处于平飞阶段,飞行高度较低,俯仰角变化很小,因此可以忽略俯仰信息,建立二维定位模型。如果观测器不机动,根据仅测角的可观测性分析,同时估计目标位置和速度的仅测角定位系统不具有可观测性。

这里将慢速运动目标看作静止目标建模,状态方程为线性方程,测量方程为非线性方程,系统模型如下：

式中,X k为k时刻的目标运动状态变量,X=(x t y t)T,忽略目标的运动速度,βk为k时刻的角度测量值,V k为状态噪声,W k为量测噪声,均为零均值的高斯白噪声,其中Φk,k-1=I2。

对于二维仅测角定位,测量方程为

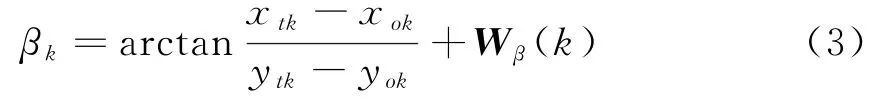
这里,方位角定义为与y轴正方向的夹角;Wβ(k)为测量噪声,服从均值为0、方差为的高斯分布。

1.2 静止目标建模的定位误差分析

慢速运动目标特点是相对于高速运动的反辐射导弹速度很小。本文研究的典型的海面运动目标运动速度为34 kn(1 kn=1 nmile/h=1.852 km/h),即17.5 m/s,最大不超过50kn(25.72 m/s)。

忽略目标的运动速度,将目标作为静止目标建模,这样系统具有了可观测性,但目标运动会带来定位误差。分别运用理论和仿真的方法分析忽略目标运动速度的可行性。这里需要说明的是,理论上观测器和目标同时作匀速直线运动时,系统不可观测,是不存在CRLB的,考虑到目标的运动速度较慢,可以近似以匀速运动观测器对静止目标的CRLB[5]来代替作误差分析。

考虑观测器和目标都作匀速直线运动,建模忽略目标速度,即取估计量x=(x t y t)T,观测量z k=(β1,β2,β3,…,βk),βk=arctan(x k/y k)+wβ,wβ为测量噪声,服从均值为0、方差为的高斯分布。x k,y k为目标和观测器的相对状态变量,根据最优估计理论[4],可以求得Fisher信息矩阵为

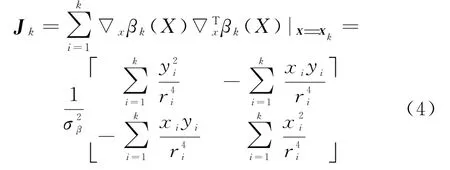
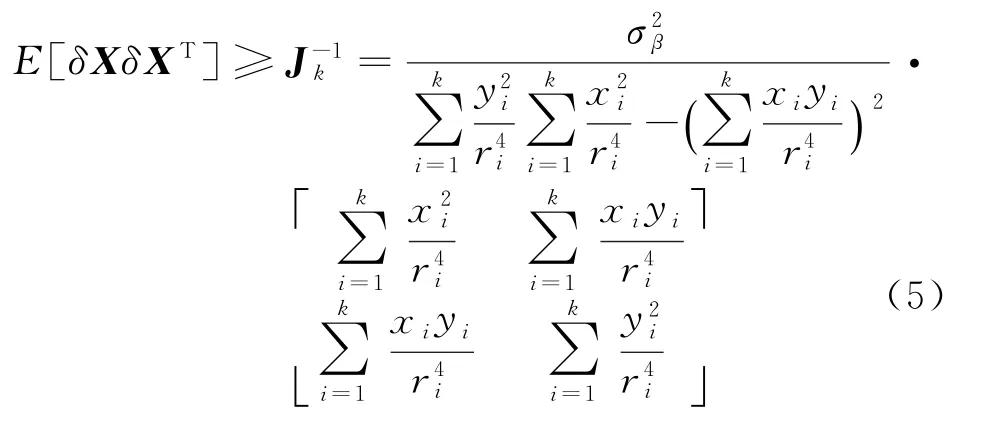
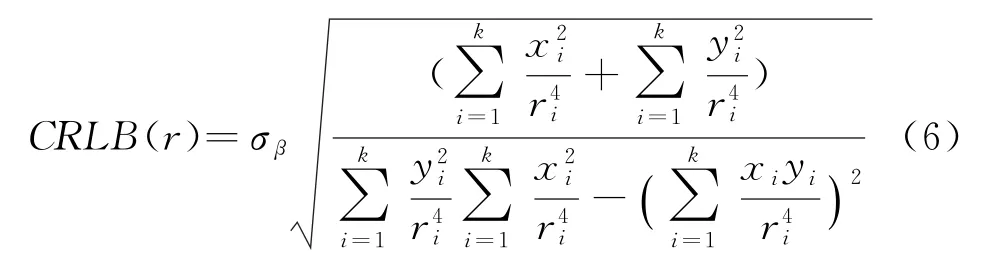
这里,x i,y i,r i每一项都包含目标的运动速度,因此目标运动速度引起的定位误差的CRLB变化无法从式(6)中看出,可以用M ATLAB来分析目标运动速度引起的定位误差的CRLB变化。

考虑观测器和目标都作匀速直线运动,角度测量误差为σβ=1°,航向以及方位角定义为与Y轴正方向的夹角,顺时针为正,逆时针为负。观测器和目标的相对运动如图1所示。

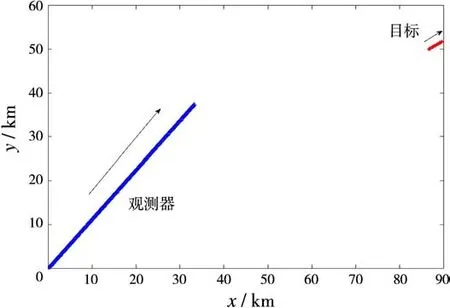
图1 观测器和目标的相对运动

图1中观测器的运动起点为(0,0)km,速度为250 m/s,航向为30°。目标的运动起点为(88.6,50.0)km,航向为60°,定位误差的CRLB随目标运动速度的变化趋势如图2所示。

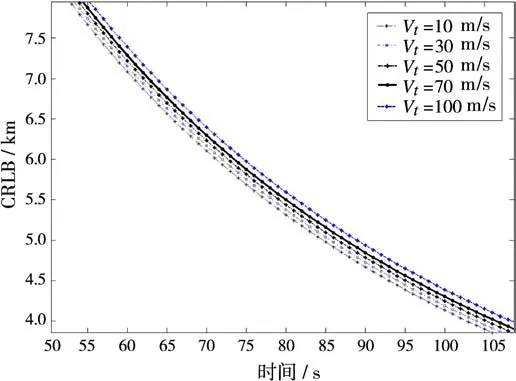
图2 目标运动速度引起的定位误差的CRLB变化

图2分析了在上述场景下,目标速度分别为10,30,50,70和100 m/s下,定位误差的CRLB变化曲线,从上图可以看出,目标的运动速度越大,忽略运动速度建模引起的定位误差就越大。但对于不超过50 kn的目标运动速度,误差变化并不大。同时考虑到末制导主动雷达对定位精度的要求为不大于2.5 km的工程需求。

同样的也可以通过仿真,分析上述场景下,忽略运动速度建模对定位算法的影响,这里算法采用EKF滤波方法,作200次Monte Carlo重复试验,RMS定位误差如图3所示。

从图3可以看出,静止目标建模时,模型和实际不符,但EKF算法仍能收敛,而考虑目标速度时,系统不具有可观测性,因此算法收敛性能并不好。

图4仿真了速度为V t=17.5,25.7和36.0 m/s时由EKF算法所计算出的定位误差对比示意图。从图中可以看出,这种模型失配系统的定位误差随着目标运动速度的增大而增大。和理论分析的结论是一致的。

因此将本文所提出的当成静止目标建模只适用于目标速度较小的情况,由于本文所研究的慢速运动最大速度不会超过50 kn,同时考虑到末制导主动雷达对定位精度的要求为不大于2.5 km,因此这里将目标看作静止目标建模对慢速目标定位,定位精度可以满足工程需求。

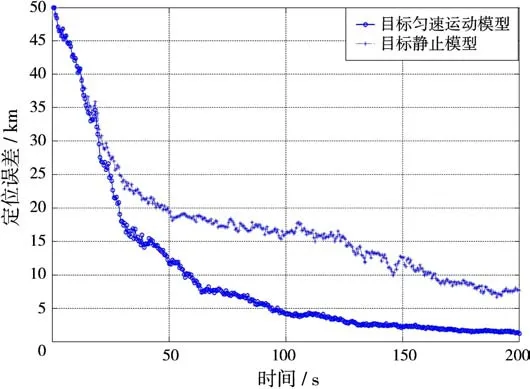
图3 静止模型和匀速直线运动模型定位误差对比

图4 目标运动速度不同时定位误差对比

2 慢速目标定位算法

2.1 基于EKF的定位算法

非线性滤波方法中,工程上应用最多的近似最优滤波方法是对非线性函数局部线性化并基于线性卡尔曼滤波器的扩展卡尔曼滤波方法(EKF),EKF在原理和计算上比较简单,在初始状态和观测精度满足一定条件的时候具有较好的效果。

由于在单站仅测角无源定位系统中,测量方程通常是非线性方程,扩展卡尔曼滤波的思路是对其进行线性化,取一阶线性化,即

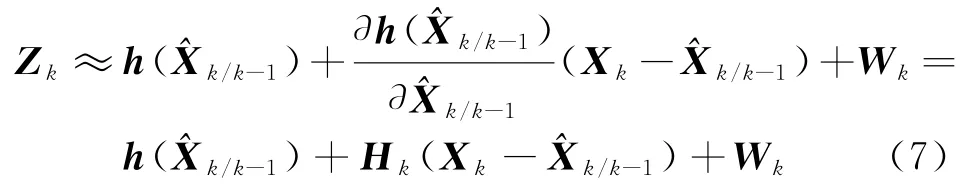
滤波过程不断地以状态更新-量测-更新的递推方式进行计算,系统扰动方差是预测精度的极限,而测量方差则决定了滤波精度的极限。

对慢速运动目标定位,若观测器无机动飞行,可以忽略目标运动速度。取状态变量X=(x t y t)T。对于本文的仅测角定位,观测方程可建立为

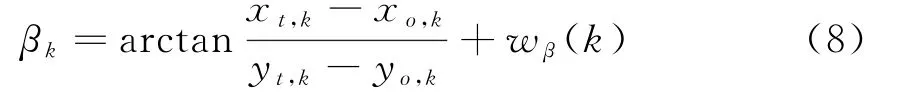
仅测角定位的Jacobin矩阵H k为

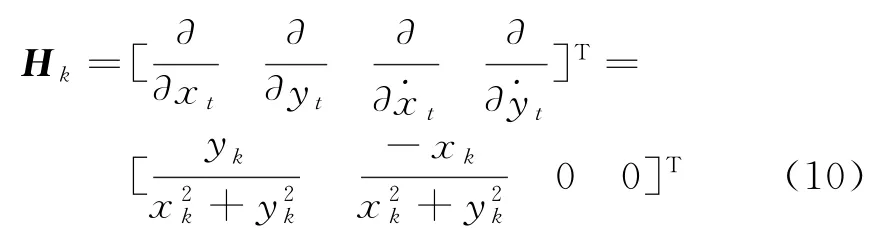
2.2 基于距离-角度划分的网格搜索法

EKF滤波算法及其改进方法的缺点是,需要足够的先验信息,一旦初始条件选得不好,就容易发散。文献[6]给出了一种无需足够准确的先验信息的更加稳健的方法,这种方法是基于状态空间离散化的网格划分。

传统网格搜索法,简称GBF(Grid Based Filter)方法。本文提到的基于距离角度划分的网格搜索法简称为RA-GBF(Range Angle Grid Based Filter)方法。GBF方法的原理描述如下：

联合概率密度函数的递推形式为

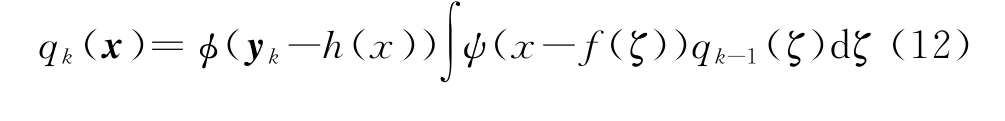
式中积分是在整个状态空间R4上,上式比较难计算的地方在于等式右边的卷积。假定不存在状态噪声,式(12)可以简化为

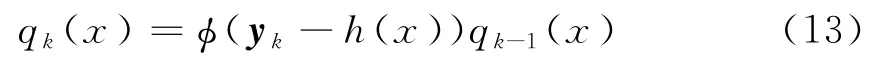
如果我们假定量测噪声一个零均值的高斯白噪声的话,即φ=N(0,σ2)。

假定目标运动是稳定的,q0(x)假定为均匀分布,于是q k(x)的具体的递推形式为

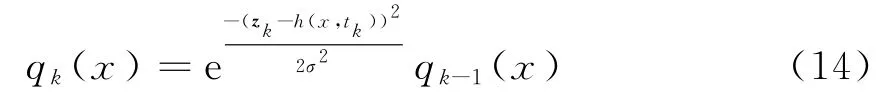
归一化之后为

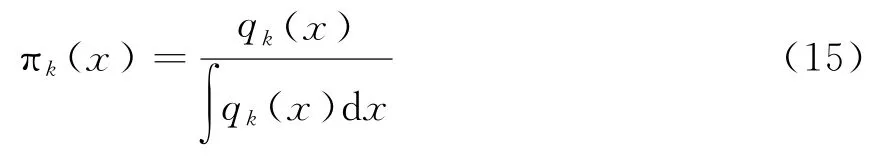
为了与EKF算法作对比,从归一化的概率密度,得到最小均方误差条件下的各种估计量

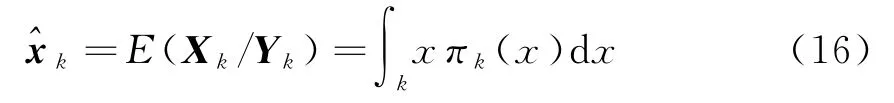
πk(x)和q k(x)是定义在整个四维状态空间R4的概率密度函数,必须在网格G上离散化。划分网格最简单的方法是,在每一个方向上的最大值和最小值之间划分网格,也即长方形网格。离散化之后,式(15)和(16)变形为

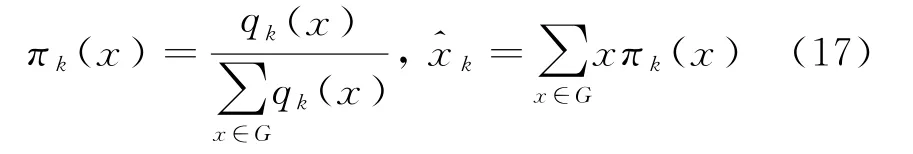
对于本文所针对的慢速运动目标,不考虑速度维,可在x,y两个维度划分网格。假设x方向的取值空间为[xmin,xmax],步长为xstep,y方向的取值空间为[ymin,ymax],步长为ystep,那么网格数N计算如下：

一般来说,网格划分得越小,定位精度就越高,但同时带来的是计算量的成倍增加。针对慢速目标仅测角定位,本文提出距离-角度划分的网格搜索法,不仅能够大大降低运算量,并且定位性能下降不是太多。RA-GBF方法的网格划分方法和GBF方法的网格划分方法区别如图5所示。

RA-GBF方法,在得到第一个角度测量值后,以观测器为原点,角度预测值β0为射线方向作距离划分,假设距离划分的范围为[rmin,rmax],步长为rstep,网格数为N r=[(rmax-rmin)/rstep],在步长一致的情况下,网格数远远小于传统的二维网格搜索。这样的网格划分方法的缺点是,在角度测量值方向上作距离划分,一是未考虑角度测量的误差,二是未考虑目标运动速度导致的目标位置在搜索范围之外。考虑这两个误差,改进网格划分范围如下：

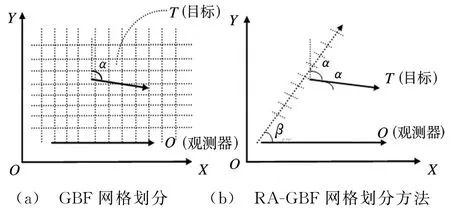
图5 两种网格划分方法对比

(1)假定测角误差为σβ,在±3σβ的扇形区域内,假设角度划分的范围为[αminαmax],每隔一定的角度步长αstep,作一条射线,在射线簇上作距离划分,这样可以有效降低因角度测量造成的固定偏差。那么网格数N r,α计算(对RA-GBF与传统的GBF进行了理论比较并给出了计算公式)如下：

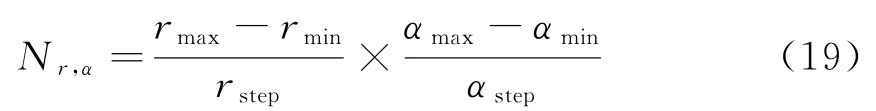
(2)考虑目标运动可能偏离搜索区域,假设目标的最大速度为V tmax,算法的仿真时间为T,那么考虑目标运动速度搜索区域应该在±V tmaxT/Rmax。

取集合(1)和(2)的并集可得到基于距离-角度划分的网格搜索范围。

RA-GBF方法的网格划分方法矫正误差之后,如图6所示。

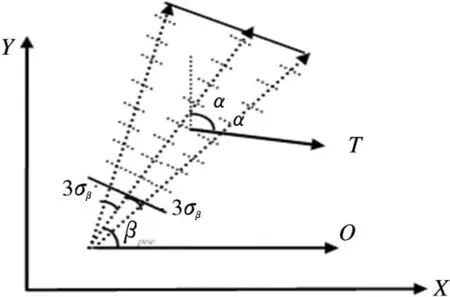
图6 矫正误差之后RA-GBF方法的网格划分方法

3 定位算法性能仿真

为了验证RA-GBF方法、EKF算法和传统GBF方法在不同条件下的定位跟踪性能,本节给出计算机仿真实例,验证忽略目标速度,观测器无机动条件下对慢速运动目标无源定位算法的性能,分别仿真了不同测角精度下算法的定位性能。

条件设置：雷达工作周期为0.5 s,仿真时间为300 s。

观测器参数：起始位置为(0,0)km,观测器速度为250 m/s,观测器航向为与Y轴正方向的夹角30°方向。

辐射源参数：起始位置为(86.6,50)km(距观测器100 km),目标速度为17.5 m/s。航向为与Y轴正方向的夹角60°方向。

仿真场景如图1所示。

仿真采用200次Monte-Carlo重复试验法,采用RMS误差统计方法进行误差统计,比较EKF算法、GBF方法以及RA-GBF方法等定位算法的性能。

(1)EKF算法的初始化

假定目标最大速度Vmax=25.72 m/s(舰船的最大巡航速度不超过50 kn),最远的探测距离为320 km,取平均距离¯R=160 km作为初始化条件。

获得第一个角度测量值β0之后,目标状态和协方差初始化如下：

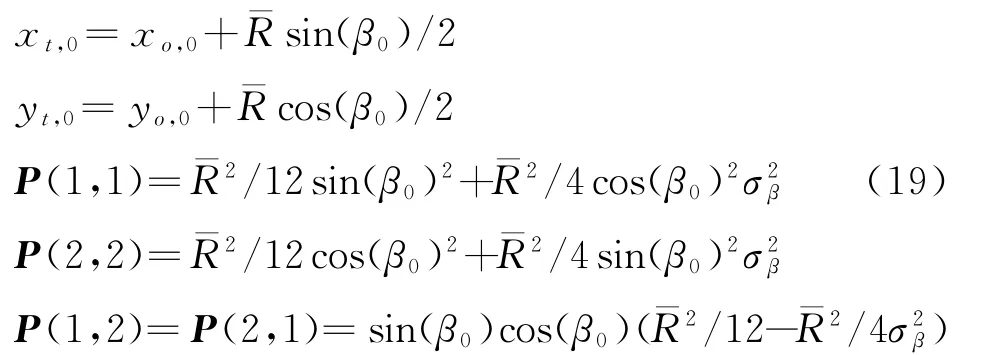
(2)GBF方法网格的划分方法

对目标距离有一定先验知识之后,网格可以划分如下：xmin=ymin=10 km,xmax=ymax=160 km,步长为1 km。

(3)RA-GBF方法网格划分方法

假定测角误差为σβ,Rmin=10 km,Rmax=160 km,步长为1 km,扇形区域为6σβ,目标运动在仿真时间300 s内产生的扇形区域为±4.73°,取两者的并集作为搜索区域,角度旋转步长为1°。

图7、图8和图9仿真在测角误差分别为0.2°,1°和2°时,EKF滤波算法、GBF方法、RAGBF方法的定位误差比较。从图中可以看出,测角误差增大时,定位误差明显变大。三种测角误差条件下,网格搜索法相比较EKF算法性能好一些。以100 s的定位误差及算法单次耗时为标准(计算机配置：CPU为Pentium 4,内存为2 GB),比较定位算法的性能,结果如表1所示。

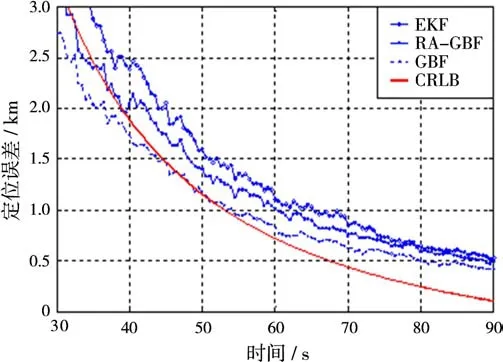
图7 测角误差为0.2°时不同定位算法的定位误差

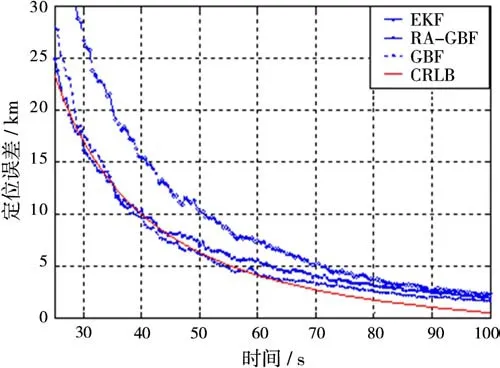
图8 测角误差为1°时不同定位算法的定位误差

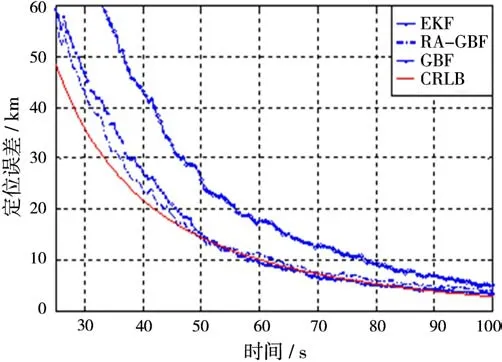
图9 测角误差为2°时不同定位算法的定位误差

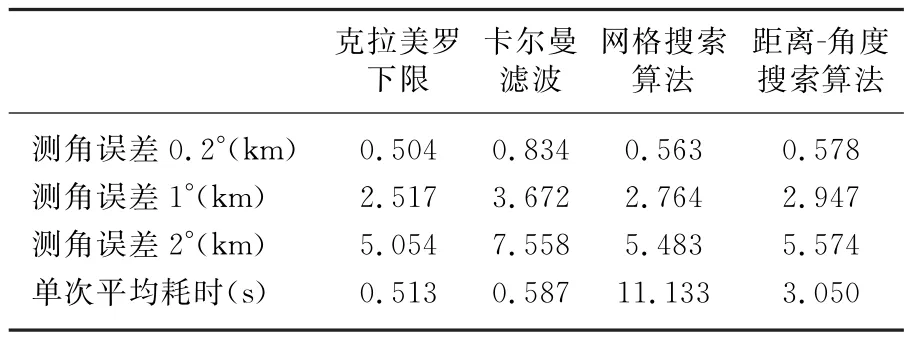
表1 不同测角误差时定位算法的定位性能比较

从表1可以看出,传统的GBF方法在全状态空间上划分网格,虽然定位精度比EKF滤波方法要高,但计算量呈倍数增加,本文针对慢速运动目标定位提出的基于距离 角度划分的RA-GBF方法定位性能和传统的GBF方法相近,计算量比GBF方法小很多。事实上,如果测角精度足够高,目标运动速度越慢,搜索区域就越小,只在初始方位线上搜索就可以达到很高的定位精度。同时,积累时间超过100 s时,定位精度可以收敛到2.5 km以下。

4 结束语

本文通过对反辐射导弹对慢速运动目标定位难点进行分析,建立了慢速目标定位的模型。将仅测角条件下,无机动单站对运动辐射源的不可观测问题转化为模型误差问题,从而在不增加观测量,同时观测器无机动的条件下,实现对慢速目标仅测角无源定位。本文提出的基于距离-角度划分的网格搜索法能有效克服传统方法运算量大的问题,可以满足末制导主动雷达对被动导引精度的需求。

[1]SUN M,HO K C.An Asymptotically Efficient Estimator for TDOA and FDOA Positioning of Multiple Disjoint Sources in the Presence of Sensor Location Uncertainties[J].IEEE Trans on Signal Processing,2011,59(7)：3434-3440.

[2]万方,丁建江.对运动目标的单站无源定位技术[J].雷达科学与技术,2011,9(1)：8-12.WAN Fang,DIGN Jian-jiang.Research on Single Observer Passive Location Technology for Moving Targets[J].Radar Science and Technology^,2011,9(1)：8-12.(in Chinese)

[3]STANSFIELD R G.Statistical Theory of DF Fixing[J].Journal of the IEE,1947,94(15)：762-770.

[4]李宗华.无机动单站对运动辐射源无源定位技术研究[D].长沙：国防科技大学研究生院,2004.

[5]罗鹏飞,张文明.统计信号处理[M].北京：电子工业出版社,1996.

[6]张文,冯道旺,姜文利.基于JPDA的单站多目标无源定位[J].航天电子对抗,2011,27(4)：47-50.