一种改进的类零相关正交多相码设计方法

孙 颖,何子述,刘 娜,李 军,林 华

(1.电子科技大学电子工程学院,四川成都611731;2.中国工程物理研究院电子工程研究所,四川绵阳621900)

0 引言

MIMO雷达是近年来的研究热点。其中波形设计问题又是雷达系统设计的基石[1-3]。现有的MIMO雷达正交波形设计的相关文献主要考虑的是自相关旁瓣,互相关以及多普勒容忍性。从第1节的分析可知发射信号的和的模糊函数等于信号成分经匹配滤波和等效发射波束形成的输出。因此对于MIMO雷达系统设计而言,我们期望和信号的模糊函数具有尽可能低的旁瓣。然而,具有良好的自相关水平和互相关水平并不能保证波形在接收端经常规处理之后还能获得高主副比。这一点可以从后文的仿真中看出。因此在设计MIMO雷达正交信号时除了自相关和互相关,还应当考虑和信号模糊函数的旁瓣性能。值得注意的是,由于MIMO波形严格正交性[4-5]对于波形设计也具有重要意义,因此波形设计时还引入了严格正交性的约束。

另一方面,在一些实际应用中,仅对发射信号在其自相关主瓣附近若干距离单元内(称为零相关区)的性能提出要求,而对远区旁瓣不作约束。研究具有零相关区域的正交波形优化设计[6-8]问题具有现实意义。文献[8]提出了一种基于遗传算法的类零相关多相码设计方法。该方法使发射信号在零相关区域具有较低的自相关旁瓣和低互相关。

本文提出了一种具有严格正交性的类零相关多相码设计方法。应用该方法设计的具有严格正交性的波形在零相关区域不但具有低自相关旁瓣和低互相关,而且在经匹配滤波和等效发射波束形成之后具有高主副比及良好的多普勒容忍性。本文同时以最小化零相关区域的自相关旁瓣水平、互相关水平,等效发射波束形成输出的距离-多普勒二维平面的主副比作为优化准则,并且约束其严格正交性,采用序列二次规划的方法优化得到发射信号的连续相位,并对连续相位进行量化得到离散的正交相位编码。该方法产生的波形足够获得超低的自相关和互相关,相对于文献[8]提高了5.8 dB。并且在接收端等效发射波束形成之后的主副比相对于文献[8]更是提高了13.44 d B。

1 信号模型

假设MIMO雷达收发阵列为均匀线阵,发射阵元数为M,接收阵元数为N。阵元间距均为半波长(d=λ/2)。每个阵元发射一个脉冲宽度为Tp的信号,信号的子码个数为L,则子码宽度等于Tp/L。第m个发射天线发射的相位编码波形可以表示为

式中,m=1,2,…,M,

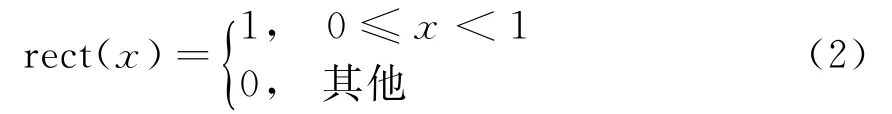
以及φm(l)是第m发射信号的第l个子脉冲的相位,对于多相码而言,φm(l)的可能取值为,其中P为相位数,也就是发射的信号是正交P相码。

在远场窄带假设下,发射信号经环境传播在目标处叠加,由目标后向散射再经环境传播到达雷达的接收端。本文分析的发射波形设计问题与接收阵列的口径无关,因此本文仅考虑一个接收阵元接收的情况,即N=1。则该接收阵元接收到的回波信号可以表示为

式中,λ和θt分别表示雷达工作波长和目标方位,2π(l-1)dsinθt/λ为第l个阵元相对于参考阵元到目标的波程差引入的相位差;fd为动目标对应的多普勒频率;n(t)为零均值的加性高斯白噪声,αt为目标回波复幅度,τ对应目标的时延。这里为了简化,不失一般性,令αt=1,τ=0。令各发射信号在目标方位处的叠加得到的信号为

则式(3)可简化为

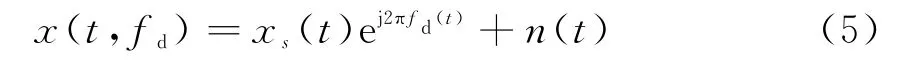
将回波信号分别与各发射信号的共轭倒相进行匹配,匹配分离出M个信号。那么回波信号与滤波器脉冲响应的匹配输出为

式中,(t)为经过匹配滤波和等效发射波束形成之后的输出噪声。注意到式(7)中的第一项是x s(u)的模糊函数,即

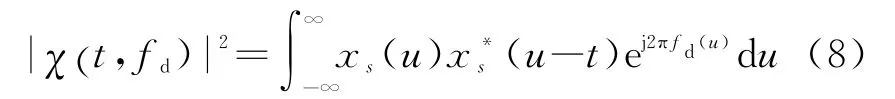
从式(4)可以看出x s(t)是发射信号的加权和。为了简化分析,我们关注θt=0°的情况。目标在其他方位上的情况将在后续研究中考虑。此时x s(t)即代表发射信号的和信号。式(7)和式(8)说明和信号的模糊函数即为信号成分等效波束形成的输出。因此和信号模糊函数具有低旁瓣在MIMO雷达波形设计中也是很重要的。然而后文的仿真显示具有良好自相关和互相关性能的相位编码波形集并不能保证它们的和信号仍然具有高的主副比。因此,在波形设计时,我们需要同时约束和信号的模糊函数,自相关和互相关。

2 波形优化设计方法

一些实际应用仅对发射信号在其自相关主瓣附近若干距离单元内(称为零相关区)的性能提出了要求,而对远区旁瓣不作约束。为了方便描述,我们首先定义零相关区。设定主瓣附近2K(K＜N-1)个距离单元为零相关区域,即需优化的距离单元是[-K,-1]∪[1,K];假定需优化的多普勒范围为(-F D,F D),将该多普勒范围按雷达的速度分辨率1/Tp划分使得该多普勒范围内包含2D-1个多普勒单元。根据模糊函数的对称性,我们只需要优化距离-多普勒平面的第一象限即可。即仅需要优化K×D的零相关距离-多普勒区域,该区域对应的距离单元范围为[1,K],多普勒单元范围为[0,D-1],这些多普勒单元对应的多普勒频率分别为fd=0.5d/Tp,d=0,2,…,D-1。MIMO雷达的非周期自相关函数和非周期互相关函数分别定义如下：

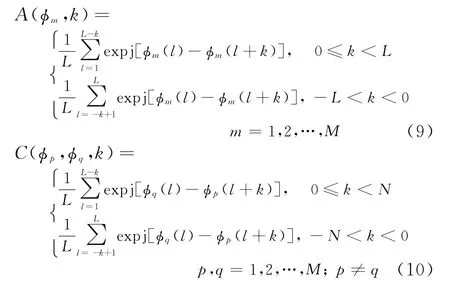
将和信号的模糊函数式(8)写成离散时间的形式：

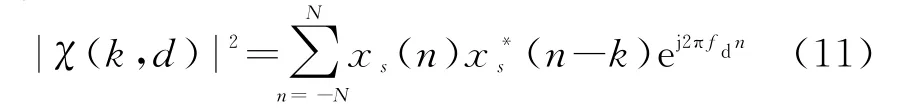
式中,k=1,2,…,K;fd=0.5d/Tp,d=0,1,…,D-1。

因此本节任务是设计能同时满足自相关函数、互相关函数以及和信号的模糊函数要求的具有严格正交性的类零相关多相码。除了严格正交的约束外,还需最小化如下的三个指标来实现：

(1)零相关区内发射信号的非周期自相关函数的峰值旁瓣,即A(φm,k),k=-K,…,K,且k≠0;m=1,2,…,M;

(2)零相关区内发射信号的非周期互相关函数峰值,即C(φp,φq,k),k=-K,…,K;p,q=1,2,…,M;

(3)零相关区内和信号的模糊函数的峰值旁瓣,即|χ(k,fd)|2,k=1,2,…,K,fd=0.5d/Tp,d=0,1,…,D-1。

则发射波形的优化的目标函数可以写为

式中,Φ为LN×1维的相位向量,Φ的每个元素的取值范围为[0,2π);为正交波形的自相关峰值旁瓣(记为APSL),为正交波形的互相关峰值(记为CP),为模糊函数在K×D的零相关距离-多普勒区域的峰值;μ1和μ2分别为互相关、和信号模糊函数权值。引入一个辅助变量z将目标函数转化为不等式约束。首先约束零相关区域内的自相关、互相关、K×D的零相关距离-多普勒区域内和信号模糊函数的旁瓣,令它们均小于等于辅助变量z,这样的整体约束使得自相关旁瓣和互相关,以及在K×D的零相关距离-多普勒区域内旁瓣幅度分布更均匀;而后极小化变量z,即极小化均匀分布的自相关旁瓣、互相关、指定距离-多普勒区域模糊函数旁瓣。通过这样的手段使得设计的波形具有低自相关旁瓣、互相关,和信号的模糊函数具有高主副比和良好的多普勒容忍性。因此式(12)转换为如下多约束的非线性规划的优化问题：

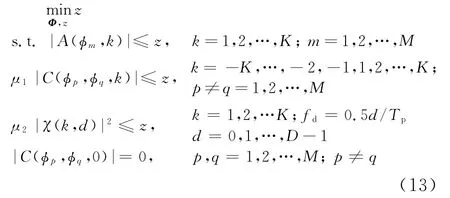
式中,z为约束的辅助变量,同时也是目标函数。

利用最优化算法中的序列二次规划(SQP,sequential quadratic programming)[9]可以求解式(13)中的优化问题。SQP是针对非线性优化的一种迭代算法。它求解的是一系列的优化子问题,每个子问题对有约束的目标函数的二次模型进行优化。当目标函数和约束均为二次连续可微时,就可以采用SQP方法进行求解。因此初始相位向量Φ0以及优化结果Φopt均为连续相位。该算法在M ATLAB中也有相应的程序包。采用M ATLAB优化工具包中的fmincon函数即可求解式(13)中的优化问题,此时fmincon函数调用了SQP算法。值得注意的是相位向量Φ的初始化问题,即Φ0的每个元素都应服从[0,2π)的均匀分布。

另外,实际应用中,优化得到的连续相位还需进行相应的量化转化为离散的正交相位编码波形。根据发射机所能提供的相位编码相位数P,按照下式能方便地将优化的连续相位量化为P相的正交相位编码：

3 仿真结果

假设MIMO雷达的发射通道数M=3,每个通道发射相位编码的子码个数L=128,脉冲宽度Tp=25.6μs,雷达工作波长λ=0.25 m。 零区域取与主瓣相邻的40个距离单元,即K=20;取多普勒域范围为[-2/Tp,2/Tp],该多普勒范围对应的目标径向速度范围为[-9765 m/s,9765 m/s]。按速度分辨率0.5/Tp采样,则正多普勒轴[0,2/Tp]包含了D=5个多普勒单元。令μ1=μ2=1,采用序列二次规划算法求解式(13)描述的优化问题,优化得到的连续相位按式(14)量化为128相码。表1为本文方法得到的128相码的相位序列,其中p,p∈(0,1,2,…,127)代表的分别代表的相位。

表1 本文方法得到的128相码

则按照表1中的相位序列产生的3个发射波形自相关和互相关归一化曲线如图1所示。

图2为图1中零相关区域的放大图。图1和图2中的实线代表的是按本文方法设计的波形的自相关和互相关;虚线为文献[8]中的波形设计结果的自相关和互相关。从图2的互相关曲线可以看出,实线在零点处(即k=0),其互相关幅值为0。即满足严格正交性。本文方法在零相关区域内的APSL和CP分别为-24.55 dB和-24.52 dB。而在相同条件下,即相同的序列个数和序列长度,文献[8]中主瓣附近的旁瓣峰值为0.1154(-18.75 dB)。本文方法对比文献[8]改善了近5.8 dB。需要说明的一点是,文献[8]中基于遗传算法设计得到的四相码正交相位编码,它随相位数P的增大并不会有多大改变[10]。

下面对发射波形经匹配滤波和等效发射波束形成之后的输出进行仿真分析。本文方法产生的波形和信号的模糊函数图以及文献[8]的波形的和信号模糊函数分别如图3和图4所示。

对比图3和图4可以看出,本文方法产生的和信号其在K×D的零相关距离-多普勒区域内旁瓣峰值为-29.27 d B,文献[8]在K×D的零相关距离-多普勒区域内旁瓣峰值为-15.83 dB。相对于文献[8],本文方法在距离维上的主副比改善13.44 dB。从文献[8]的仿真结果也可以看出,仅仅优化发射信号的自相关旁瓣和互相关,并不能保证在接收端经匹配滤波和等效发射波束形成之后能获得期望的主副比。实际上在接收端经处理后,文献[8]的旁瓣性能恶化了2.92 dB。因此采用本文方法同时优化自相关旁瓣、互相关以及和信号的模糊函数是很有必要的。

图1 本文优化方法得到128相码的自相关和互相关

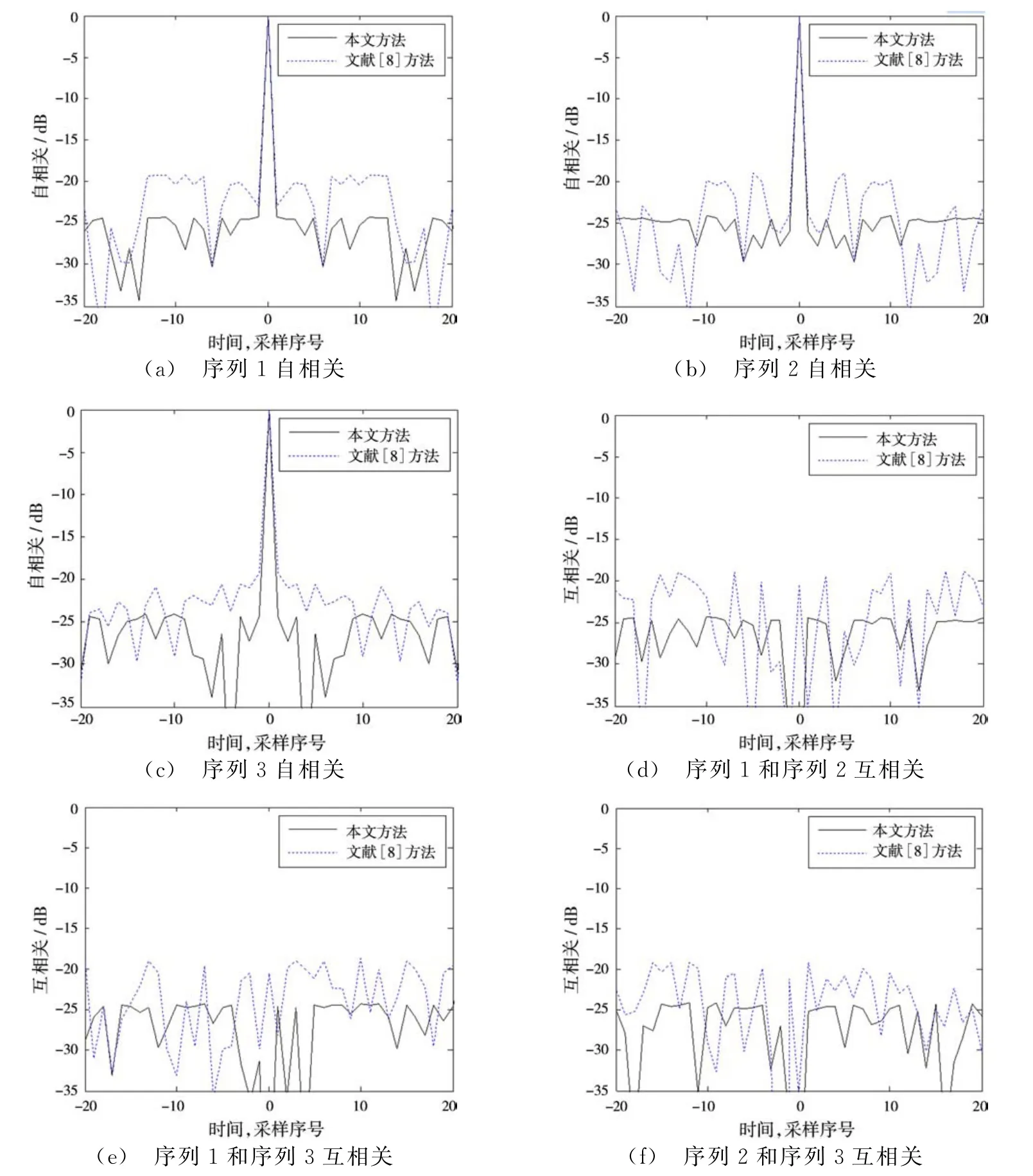
图2 零相关区域的自相关和互相关曲线

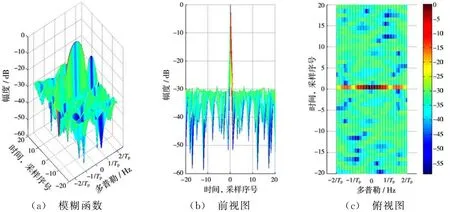
图3 本文方法设计波形的和信号的模糊函数

图4 文献[8]设计波形的和信号的模糊函数

4 结束语

MIMO雷达相关文献大多关注的是使用正交波形的情况。这些正交波形经由目标反射被接收天线接收,在接收端经过一组匹配滤波器将它们分离后再进行等效发射波束形成。根据第1节的推导可知和信号的模糊函数等于信号成分等效波束形成的输出。因此,我们期望和信号的模糊函数具有高的主副比。然而,具有良好的自相关水平和互相关水平并不能保证波形在接收端经常规处理之后还能获得高主副比。在波形设计时应当同时优化和信号的模糊函数,自相关和互相关。另一方面,一些实际应用仅对发射信号在其自相关主瓣附近若干距离单元内的性能提出了要求,而对远区旁瓣不作约束。因此,本文提出了一种基于序列二次规划算法的具有严格正交性的类零相关多相码设计方法,该方法能同时满足低自相关旁瓣,低互相关以及和信号模糊函数具有高主副比的性能以及严格正交约束的要求。值得注意的是,采用序列二次规划算法得到的编码为属于[0,2π)的连续相位。为了便于实际的工程应用,我们将连续相位量化,最终得到正交P相码波形。实际应用中能提供的相位寄存器位数越高,即P越大,越能逼近连续相位对应的正交波形所取得自相关旁瓣、互相关、和信号模糊函数主副比性能。

[1]GOGINENI S,NEHORAI A.Frequency-Hopping Code Design for MIMO Radar Estimation Using Sparse Modeling[J].IEEE Trans on Signal Processing,2012,60(6)：3022-3035.

[2]CHEN Yifan,NIJSURE Y,YUEN C,et al.Adaptive Distributed MIMO Radar Waveform Optimization Based on Mutual Information[J].IEEE Trans on Aerospace and Electronic Systems,2013,49(2)：1374-1385.

[3]陈正辉,严济鸿,何子述.MIMO雷达OFDM-LFM波形设计与实现[J].雷达科学与技术,2013,11(1)：77-81.CHEN Zheng-hui,YAN Ji-hong,HE Zi-shu.Design for MIMO Radar and Implementation of OFDM-LFM Waveform[J].Radar Science and Technology,2013,11(1)：77-81.(in Chinese)

[4]YING Sun,HE Zishu,LIU Hongming,et al.Improved Design of Binary Orthogonal Code for MIMO Radar[J].Optoelectronics and Advanced Materials-Rapid Communications,2011,5(8)：863-865.

[5]LEE N,CHUN J.Orthogonal Pulse Compression Code Design for Waveform Diversity in Multistatic Radar Systems[C]∥IEEE Radar Conference,Rome：[s.n.],2008：1-6.

[6]XU Lei,LIANG Qilian.Zero Correlation Zone Sequence Pair Sets for MIMO Radar[J].IEEE Trans on Aerospace and Electronic Systems,2012,48(3)：2100-2113.

[7]李玉博,许成谦,李刚,等.一类三元多子集零相关区序列集构造法[J].电子与信息学报,2012,34(12)：2876-2880.

[8]金明,廖桂生,李军.基于遗传算法的类零相关多相码设计[J].系统工程与电子技术,2010,32(1)：14-17.

[9]胡亮兵,刘宏伟,吴顺君.基于约束非线性规划的MIMO雷达正交波形设计[J].系统工程与电子技术,2011,33(1)：64-68.

[10]刘波.MIMO雷达正交波形设计及信号处理研究[D].成都：电子科技大学,2008.