噪声对基于PAF的PRBC-CW信号识别的影响

刘 静,赵惠昌,张淑宁

(1.中国电子科技集团公司第三十八研究所,安徽合肥230088;2.南京理工大学电子工程与光电技术学院,江苏南京210094)

0 引言

干扰和抗干扰是电子战的重要形式,而要实施有效的干扰,必须对敌方信号进行实时侦察截获,并获取对方信号的调制方式、估计调制参数等信息。伪码调相连续波(Pseudo-random biphasecoded CW,PRBC-CW)近程雷达是利用伪随机m序列的自相关函数类似于白噪声相关函数的随机特性而工作的。该体制雷达抗干扰能力强,具有良好的距离分辨率和距离截止特性[1-3],现已成为近程探测雷达的重要发展方向之一,因此研究伪码调相连续波信号的识别和特征参数提取具有重要的意义。

目前已有不少文献提出各种对伪码调相信号的识别和分类方法[4-6],取得较好的结果,然而这些识别方法大都是采用谱相关技术[4-5]或者Cohen[6]类时频分析技术,算法复杂度高、运算量大,不适合应用于近程雷达的侦察识别。周期模糊函数(Periodic ambiguity function,PAF)是对连续波雷达信号进行分析研究和波形设计的有效工具,它描述了信号的全部特性,不同形式的信号具有不同的模糊函数,为相关域表示,算法比较简单,可以通过快速傅里叶变换实现,能够满足近程雷达侦察实时处理技术的要求[7-10]。本文研究基于PAF的伪码调相连续波信号的识别,分析在有限采集时间下,噪声对基于周期模糊函数的伪码调相连续波近程雷达信号参数提取的影响,推导在模糊函数变换中由噪声所产生项(不期望项)的均值和方差,并进行了仿真验证。

1 基于PAF的PRBC-CW近程雷达信号识别

1.1 周期模糊函数理论

周期模糊函数是研究、分析周期连续波信号及进行波形设计的有效数学工具,它表示时延频偏平面的相关,为相关域表示。

设周期调制连续波信号复包络u(t)是周期为T的周期信号,即

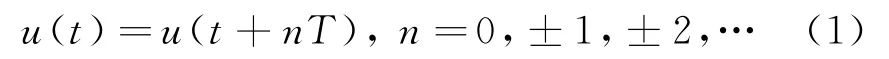
则信号的单周期模糊函数[7,9]可以表示为

式中,τ为时延,ξ为频率偏移,符号“∗”表示共轭。可以看出,式(2)可以通过FFT来实现。

若采用的参考信号长度为发射信号调制周期的N倍,则在时延为τ、多普勒频率为ξ时的周期模糊函数为[7-9]

由此可以看出,周期调制连续波信号的模糊函数|χNT(τ,ξ)|是由其单周期模糊函数|χT(τ,ξ)|与函数|sin(πξNT)/Nsin(πξT)|的乘积得到,其中N为调制信号周期数。

1.2 基于PAF的PRBC-CW近程雷达信号参数估计

在伪码调相连续波体制雷达中,伪随机二项码调制信号的复包络可以表示为

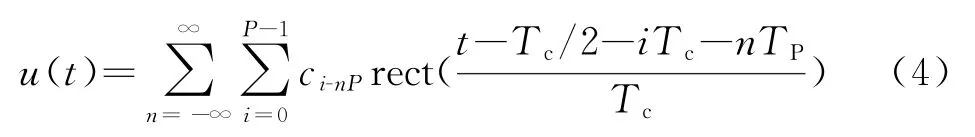
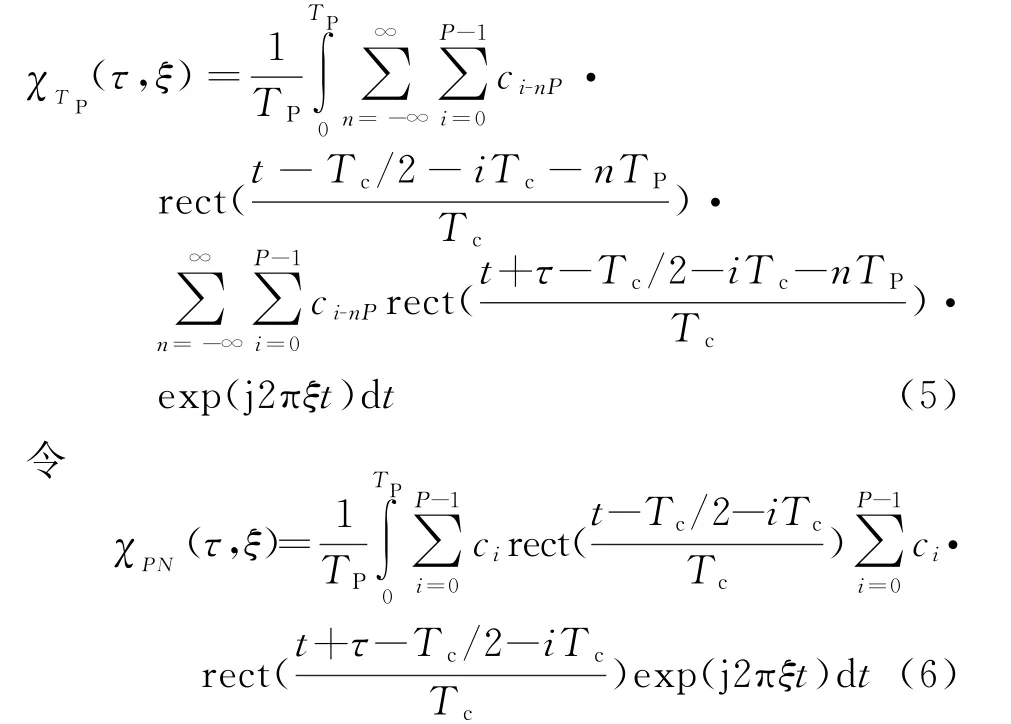
则式(5)经过整理化简后,得到伪随机二项码调制连续波信号的单周期模糊函数为

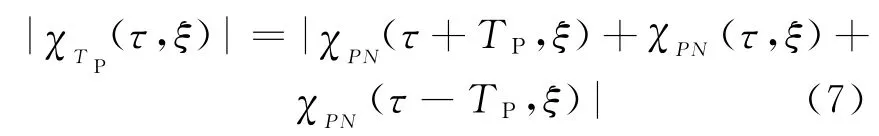
可以看出,伪随机二项码调制连续波信号的单周期模糊函数是由χPN(τ,ξ)时移后叠加而得。由模糊函数的定义及单载频矩形脉冲信号的模糊函数推导过程[11]知,χPN(τ,ξ)即为脉冲宽度为TP、子脉冲宽度为Tc的伪随机二相编码脉冲压缩信号的模糊函数。对于伪随机二相编码脉冲压缩信号的模糊函数,有很多文献已经介绍过[11-13],其中文献[11]给出了二相编码脉冲压缩信号的一般模糊函数表达式,并介绍了一种13位巴克编码信号模糊函数的推导方法,文献[12]推导了m序列二相编码信号的模糊函数表达式,并对其特性进行了详细的分析,本文在此就不详细分析了。

将式(7)代入式(3)得到伪码调相连续波近程雷达信号的周期模糊函数为

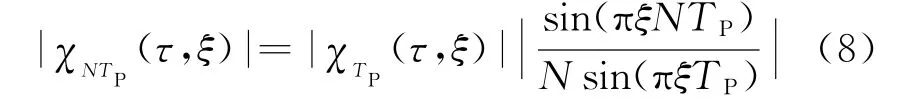
由式(5)、(7)、(8)知,PRBC-CW信号周期模糊函数峰值之间的距离即为调制周期TP,主峰半功率处在时延轴上的宽度即为码元宽度Tc,如图1所示。因此,可以通过周期模糊函数切割的值来估计PRBC-CW信号的参数。显然,此种求取伪码参数的方法只是在求信号模糊函数时运算量比较大,但可以通过FFT的快速算法来解决,在求取参数的过程中将二维搜索分别映射到一维时延轴上和多普勒频移轴上,使运算量大大减小,节省了计算时间,有利于近程雷达实施快速有效干扰。

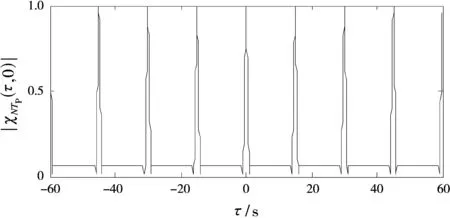
图1 PRBC-CW信号周期模糊函数切割图(Tc=1s,P=15)

2 噪声对PRBC-CW近程雷达信号参数估计的影响

在近程雷达侦察过程中,设接收机截获得到的信号为

式中,n(t)为均值为零的加性平稳噪声;s(t)为截获得到的载波频率为f0的有用信号,即

则x(t)的模糊函数[10]为

然而,在实际运算中模糊函数是以χx(τ,ξ)的离散形式来计算的,在采样频率为fs时的离散形式为

式中,N为实际接收信号的总采样点数。在计算中,由于采样时间的有限,式(11)中的噪声项并非恒为零,显然这会对参数的估计带来影响。

可以看出,当数据点数N趋于无穷大时,式(14)中的(m,k)和(m,k)将趋向于零,当τ≠0时的(m,k)也趋向于零。此时x(n)的模糊函数估计值(m,k)将趋向于理论值χx(τ,ξ)。然而在实际的信号处理中,数据长度N为有限值,由于噪声的存在而产生的项(m,k)、(m,k)及τ≠0时的(m,k)均不为零,从而对基于模糊函数的参数估计带来了影响。

不失一般性,设n(t)为均值为零的复高斯白噪声,实部和虚部独立同分布,既有,总方差为,自相关函数为,信号s(t)的平均功率为s,则有均值

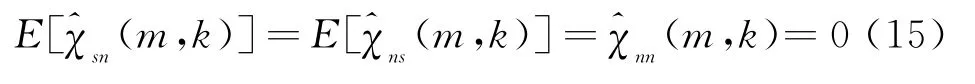
对于(m,k)的方差

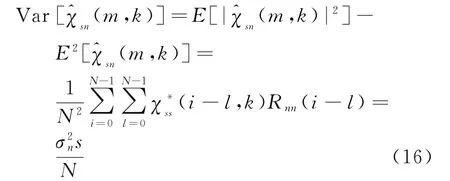
同理(m,k)的方差

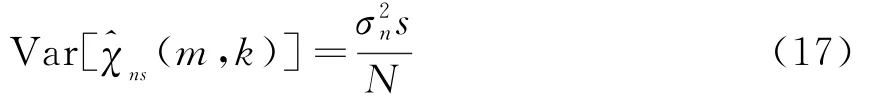
由高斯白噪声的性质

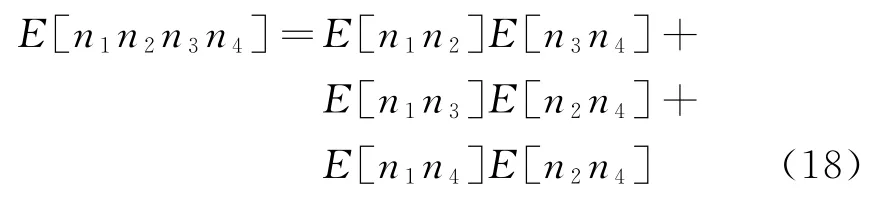
则(m,k)的方差为

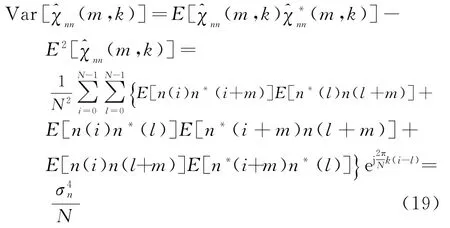
可以看出,若待分析信号中含有高斯白噪声,则在模糊函数变换中,信号与噪声的交叉项均值为零,方差为;噪声项的均值也为零,方差为。显然,截获信号的模糊函数噪声项方差与噪声功率大小和有限采样时间有关,随着采样数据的增大,噪声的方差趋于无限小。因此,为了提高参数估计精度,在不影响实时性的情况下可以适当增加采样时间。

3 仿真分析

根据第2节所说参数估计方法,通过蒙特卡罗数字仿真实验对噪声环境下的侦察信号进行识别。取伪随机序列长度为15,码元宽度分别为Tc=20ns及Tc=100ns的伪码调相连续波近程雷达信号,在采样时间为6个伪码周期和30个伪码周期的条件下来分析平稳噪声对基于周期模糊函数的伪码调相连续波信号参数估计的影响,仿真结果如图2所示。图中,纵轴为归一化的均方误差(NRMSE),横轴为输入信号的信噪比(SNR)。

图2 参数估计NRMSE随SNR变化的曲线分析

从图中可以看出,码元宽度Tc和伪码周期Tp的估计归一化均方误差随着信噪比的增加而减小,而且截取6个伪码周期的信号进行参数估计时,码元宽度Tc的估计方差在信噪比为0 dB时才趋于稳定,而截取30个伪码周期信号进行参数估计时,Tc的估计方差在-5 d B时基本趋于稳定;同样地,伪码周期Tp的估计方差在6个伪码周期时在-5 d B趋于稳定,而取30个伪码周期时在-10 dB左右就基本趋于稳定。显然,在采样频率一定时,随着采样数据的增加,噪声对参数估计精度的影响越来越小,这与理论分析结果是一致的。

4 结束语

模糊函数为相关域表示,可以通过快速傅里叶变换来实现,算法简单,能够满足近程雷达侦察实时处理的要求。本文研究基于PAF的伪码调相连续波信号的识别,分析在有限采集时间下,噪声对基于周期模糊函数的伪码调相连续波近程雷达信号参数提取的影响,并进行了仿真验证。结果表明,截获信号的模糊函数噪声项方差与噪声功率大小和有限采样时间有关,随着采样数据的增大,噪声的方差趋于无限小,对参数估计精度的影响也越来越小。而采样时间直接决定了计算量的大小,因此,为了提高参数估计精度,通常需要在估计精度和计算量之间折衷考虑。

[1]张居正.伪随机码调相引信原理及设计[J].制导与引信,2000,21(3)：1-7.

[2]徐立平,谢锡海,曹志谦,等.伪码引信的数字多相滤波和频域脉冲压缩[J].探测与控制学报,2009,31(5)：5-10.

[3]DAMIAN F A,ALBERT M K.PRC/FM CW Radar System：US,4241347[P].1980-06-28.

[4]谢然,张效义,田鹏武.一种基于循环谱的MPSK信号符号速率估计方法[J].计算机应用研究,2011,28(6)：2294-2296.

[5]ZHANG Hai-jian,LE R D,TERRE M.Signal Detection for OFDM/OQAM System Using Cyclostationary Signatures[C]∥IEEE 19th International Symposium on Personal,Indoor and Mobile Radio Communications,Cannes,France：[s.n.],2008：1-5.

[6]UPPERMAN T L O.Elint Signal Processing on Reconfigurable[sic]Reconfigurable Computers for Detection and Classification of LPI Emitters[D].Monterey,USA：Naval Postgraduate School,2008.

[7]LEVANON N,FREEDOM A.Periodic Ambiguity Function of CW Signals with Perfect Periodic Autocorrelation[J].IEEE Trans on Aerospace and Electronic Systems,1992,28(2)：387-395.

[8]LEVANON N.The Periodic Ambiguity Function-Its Validity and Value[C]∥2010 IEEE Radar Conference,Washington,DC,USA：IEEE,2010：204-208.

[9]PACE P E.Detecting and Classifying Low Probability of Intercept Radar[M].Norwood,MA,USA：Artech House,2009：67-78.

[10]李雪梅,陶然,王越.时延估计技术研究[J].雷达科学与技术,2010,8(4)：362-371.LI Xue-mei,TAO Ran,WANG Yue.Summary of the Time Delay Estimation[J].Radar Science and Technology,2010,8(4)：362-371.(in Chinese)

[11]林茂庸,柯有安.雷达信号理论[M].北京：国防工业出版社,1984：153-178.

[12]周新刚.典型无线电引信抗干扰性能测度理论和方法研究[D].南京：南京理工大学,2010：65-80.

[13]LIN C T.On the Ambiguity Function of Random Binary-Phase-Coded Waveforms[J].IEEE Trans on Aerospace and Electronic Systems,1985,21(3)：432-436.