基于粗糙集和BP神经网络的粮食产量预测研究

徐兴梅，曹丽英

（吉林农业大学信息技术学院，长春 130118）

吉林省是重要农业大省，是国家粮食主产区之一，盛产玉米、大豆、水稻和各种薯类等农产品。在农业生产过程中，影响粮食产量因素包括国家调控政策、市场状况、自然灾害、土地墒情、施肥量、灌溉情况、耕种面积等。如何准确掌握粮食生产状态，提高粮食产量，分析预测粮食生产变化规律和趋势具有重要意义。

随着计算机技术、农业信息化和3S技术发展，研究者对粮食产量的预测进行大量研究，如遥感预测法[1]、回归分析法[2]、时间序列分析法[3]、主成分分析法[4]、灰色系统理论法[5]等，每一种方法都有优缺点，造成预测的片面性，预测误差较大，难以准确预测粮食生产发展趋势。

Pawlak 提出粗糙集理论（Rough set theory）[6]，在处理大量数据、消除冗余信息等方面效果较好，但是对噪声数据很敏感。人工神经网络具有鲁棒性强、对噪声数据不敏感优点，但也有学习速度缓慢、网络训练过度缺点[7]。鉴于粗糙集理论和神经网络算法拥有很强优势互补性，因此本文将二者融合，利用粗糙集理论对诸多因素进行属性约简，找出主要影响因素，剔除冗余信息，降低数据维数，在此基础上建立粗糙集-BP神经网络（RSBP）预测模型，使其在粮食产量预测中发挥作用。

1 研究区域、材料与方法

1.1 研究区域

吉林省位于中国东北中部，地处东经122～131°、北纬41～46°之间，面积为18.74万hm2，其中耕地553.78万hm2，占总面积的28.98%。吉林省属温带季风气候，有较明显的大陆性。吉林省主要粮食作物有玉米、水稻、谷子、大豆、高粱、小麦等。

1.2 数据来源

数据来源于吉林省统计年鉴，将吉林省1980～2012年粮食产量作为研究数据，结合领域专家的意见，选取化肥施用量（x1）、大牲畜年底头数（x2）、粮食播种面积（x3）、农业机械总动力（x4）、有效灌溉面积（x5）、农村用电量（x6）、农村居民家庭平均每人全年纯收入（x7）、农村人均居住面积（x8）等8个影响因素进行分析。

1.3 粗糙集

粗糙集理论是研究不完备信息的有效工具，例如不精确（Imprecise）、不一致（Inconsistent）、不完整（Incomplete）的各类信息，优点是能直接对数据进行合理分析和正确推理，不需要预先给定某些特征或属性的数量描述，而是直接从给定问题的描述集合出发，通过不可分辨关系和不可分辨类确定问题的近似域，并发现其中隐含的知识及潜在的规律，因此，粗糙集理论广泛应用于机器学习、模式识别、支持向量机、人工智能[8-9]等领域。

定义1 四元组S=（U，A，V，f）是一个信息系统，其中U称作论域，即对象的非空有限集合；A=CD代表所有属性的非空有限集合，其中条件属性C和决策属性D不相关；V称作值域，即属性值的范围；f表示信息函数。

定义2每个属性子集R∈A决定了一个二元不可区分关系IND（R），即

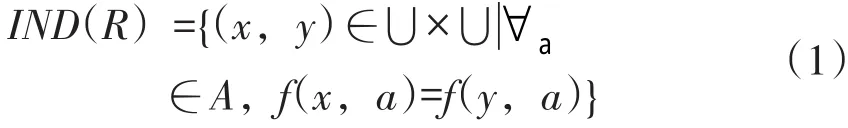
IND（R）构成U的一个划分，也就是U/IND（R），其中任一元素称为等价类，信息系统S=（U，A，V，f）也称作知识A。

已知U/IND（R）={X1，X2，…，Xn}，则知识R的信息量定义为

定义3S=（U，A，V，f）是一个信息系统，属性a在A中的重要性定义为

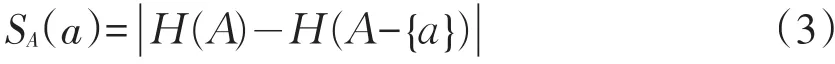
在（3）式中，当S（Aa）＞0时，称a∈A在A中是必要的；当S（Aa）=0时，a是冗余的。

根据离散数据表可以评价属性依赖度和重要度等指标，因此需要对连续的样本数据值进行离散化处理[10]，常用的处理方法有等距离法、等频率法、最大熵法等。根据离散化后的知识建立原始决策表，利用粗糙集理论知识对决策表进行属性约简处理[11-12]，属性约简要求在保证知识库分类和决策能力不变的条件下，删除不重要或不相关属性[13]。本文采用Johnson约简算法[14]，意义明确，在多数情况下可以得到最小约简集合[15]。一般步骤为：

输入：决策表S=（U，A，V，f），其中A=CD；

输出：决策表S的一个相对约简Red。

① 令Red=φ，As=φ，ωa（iA）s=0；

② 计算可分辨矩阵M，As={mij；mij≠φ}；

③ 计算属性ai在As中出现的次数ωa（iAs）；

④ 选择使得ωa（iAs）最大的属性记作a，Red=Red{a}；

⑤清除掉As中包含a属性的全部集合；

⑥当As=φ时，则停止，否则转入③步骤。

1.4 BP神经网络算法

Rumelhart等提出误差反向传递学习算法（即BP算法），这一算法的提出可实现多层网络构想[16-17]，BP算法不但有输入层节点、输出层节点[18-19]，还可以有1个或多个隐含层节点，一般称为三层前馈网或三层感知器，如图1所示。输入层各神经元负责接收来自外界的输入信息，并传递给中间层各神经元；中间层是内部信息处理层，可以设计为单隐层或者多隐层结构；最后一个隐层传递到输出层各神经元的信息，经过一步处理后，完成一次学习的正向传播处理过程，由输出层向外界输出信息处理结束。BP网络被看成是一个从输入到输出的高度非线性映射。

图1 BP神经网络结构Fig.1 Structure of BP neural network

BP神经网络的特点是各层神经元仅与相邻层神经元之间相互全连接，同层内神经元之间无连接，该算法的学习过程由正向传递和反向传递两部分组成。在正向传递过程中，输入信息从输入层经隐含层逐层进行处理，然后传向输出层。每一层神经元的状态仅仅影响下一层神经元状态。如果输出层得不到期望的输出值，则转入反向传递过程，将误差信号沿着原连接通道返回，通过修正各层神经元的权值，使得误差信号达到最小。

如果把神经网络看成从输入到输出的映射，则这个映射是一个高度非线性映射[20]。这类问题的处理流程可以分为BP神经网络的构建、训练和预测三个步骤，如图2所示。

图2 BP神经网络流程Fig.2 Flow chart of BP neural network

BP神经网络算法使用优化中的梯度下降法把一组样本的输入/输出问题转换为一个非线性优化问题。设含有n个节点的任意网络，各节点的特性为Sigmoid型。指定网络只有一个输出y。任一节点i的输出为Oi，并设有N个样本 （xk，yk）（k=1，2，3，…，N），对某一输入xk，网络输出为yk，节点i的输出为Oik，节点j的输入为

并将误差函数定义为

当j为输出节点时，则有

如果有M层，而第M层仅含输出节点，第一层为输入节点，则BP算法的运算过程如下：

第1步：选取初始权值W；

第2步：重复下述过程直至收敛；

1.对于k=1到N

（1）计算Oik，netjk和的值（正向过程）；

（2）对各层从M到2反向计算（反向过程）；

2.对同一节点j∈M，由式（1）和（2）计算δjk；

从上述BP神经网络算法可以看出，BP模型把一组样本的I/O问题转换为一个非线性优化问题。使用的是优化中最普通的梯度下降法，可以实现输入和输出的任意非线性映射，具有高度非线性和很强的自适应学习能力。因此被广泛应用于函数逼近、模式识别、经济预测等领域。

2 结果与分析

2.1 基于粗糙集理论的数据预处理

本文使用的是Rosetta软件，Rosetta软件是一个用于简化模型的通用型工具，提供多种数据预处理功能，如决策表补齐、决策表离散化等及其算法，同时提供粗糙集中常见的约简和规则的获取算法，支持从数据预处理到预测和分析规则的全过程，是一个实用的粗糙集理论软件和试验平台。

试验过程如下：将影响粮食产量的8个影响因素作为条件属性集C={x1，x2，…，x8}，将粮食产量作为决策属性D={d}。首先对原始数据进行离散化处理，计算每个影响因素的两年相对增量比，通过离散编码方式得到影响因素布尔表，结果见表1。

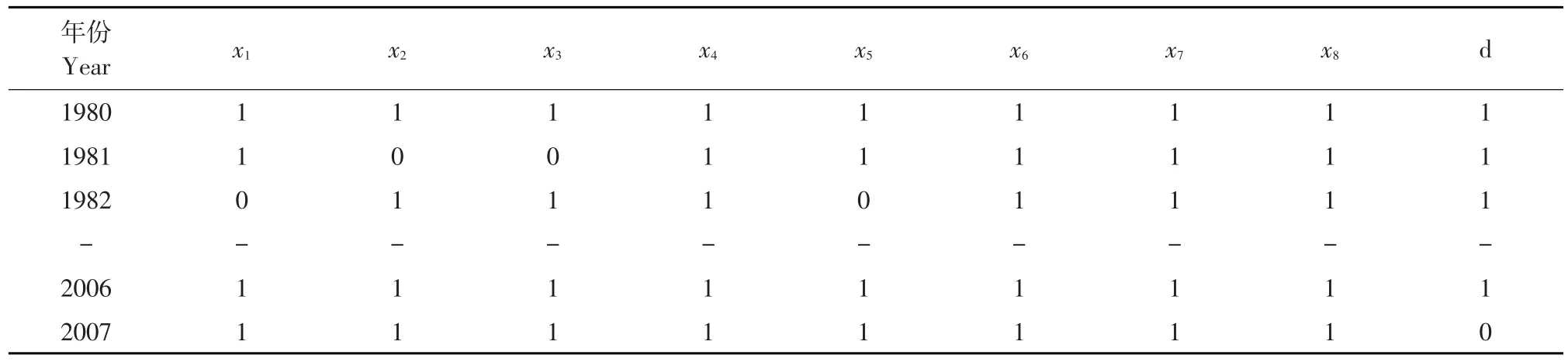
表1 影响因素Table 1 Boolean table of the influencing factors

使用Johnson算法分别进行属性约简和规则提取，经计算，最后得到最小属性约简为{x1，x2，x3，x5，x7}，约简后的影响因素为5个，即化肥施用量（x1）、大牲畜年底头数（x2）、粮食播种面积（x3）、有效灌溉面积（x5）、农村居民家庭平均每人全年纯收入（x7），去除3个冗余影响因素。可见，化肥施用量、粮食播种面积及有效灌溉面积增加必然导致总体粮食产量增加。

在得到属性约简结果后，可以得到一系列的决策规则，本试验共产生14条规则。在分类原则及决策能力保持不变的情况下，进行约简后从中选取可信度和覆盖度都较高的11条有价值主要规则，这充分体现粗糙集理论数据约简、规则约简的优势。

2.2 RSBP神经网络的建立

数据归一化方法是神经网络预测前对数据常做的一种处理方法，数据归一化处理把所有数据转化为[0，1]之间的数，目的是取消各维数据间数量级的差别，避免因为输出数据数量级差别较大而造成网络预测误差较大。归一化的方法主要采用的函数形式是：

在（4）式中，为数据序列中的最小数，为数据序列中的最大数。

对数据进行归一化处理后，采用3层BP神经网络模型，利用原来的8个变量作为输入变量建立BP神经网络模型，对数据进行训练，训练函数使用Trainlm函数，隐含层及输出层传递函数分别使用S型正切函数Tansig函数和Purelin函数，训练目标为0.01，最大训练次数为1000次。对设计好的神经网络模型进行训练，训练稳定后的训练结果为共经历42次迭代，且均方误差在34次迭代时达到1041.2238，网络平滑地收敛于全局极小值。

利用约简后的数据建立RSBP模型，训练样本采用属性约简后的11条数据，输入层节点数为5，输出层节点数为1，根据经验及网络的实际训练情况，隐含层节点数确定为11，RSBP神经网络的最终结构为（5，11，1）。在相同的条件下对设计好的神经网络模型进行训练，训练得到的均方误差曲线如图3所示。可见，训练结果很理想，共经历31次迭代，且均方误差在25次迭代时达到751.1991，网络很平滑地收敛于全局极小值。

图3 RSBP网络训练结果Fig.3 Results of RSBP network training

通过分析，不难发现RSBP模型相对于传统的BP模型具有更快的收敛速度，更精确的均方误差，优化后的神经网络模型具有更好的使用效果。

2.3 结果比较

选择2008～2012年吉林省粮食产量数据对该网络进行测试，并与未经粗糙集处理而直接建立BP模型预测结果比较，结果如表2和图4。

表2 吉林省2008～2012年粮食产量预测结果Table 2 Forecast of grain output in Jilin province 2008-2012

图4 吉林省2008～2012年粮食产量预测结果对比Fig.4 Forecast comparison of grain output in Jilin Province 2008-2012

和单一的BP神经网络模型相比，RSBP神经网络模型输入层数据由原来8个降为5个，训练时间由原来95s降为68s。由表2可见，未经粗糙集处理的BP预测模型的预测平均误差为5.4867%，RSBP模型的预测误差为4.6737%，RSBP模型的预测精度更高；从图4中可以看出，RSBP模型的预测的趋势较BP模型的预测趋势更加明显，更接近实际产量。

可见，RSBP神经网络能有效减少输入神经元的数量，简化网络结构，减少训练时间，提高神经网络的学习效率，将基于粗糙集和BP神经网络的粮食产量预测模型应用到实际农业生产中，能提高粮食产量预测的有效性和正确率。

3 讨 论

本文运用粗糙集理论，对影响粮食产量预测精度的条件属性进行约简，将约简后的数据作为BP神经网络的输入变量建立RSBP模型，并与传统BP神经网络的预测结果进行比较。结果表明，传统BP预测模型的预测误差为5.4867%，RSBP模型的预测误差为4.6737%，证明RSBP模型的预测精度比传统BP神经网络模型高。

①仿真对比试验结果表明，相对于单一的预测方法，本文使用的方法预测速度更快、预测精度更高，可解决粮食预测因素复杂情况下的非线性预测问题。该方法将先进的计算机技术融入到实际生产实践当中，对于不确定性和不精确性问题提供解决途径，拓展粗糙集理论、BP神经网络算法等数据挖掘技术的应用领域。

②粗糙集理论与BP神经网络算法的组合使用可消除冗余变量，输入变量由原来的8个降为处理后的5个，减少计算复杂度，省去粗糙集单一运用时规则提取的复杂运算；同时网络训练迭代次数由42次降为31次，均方误差减少，有效克服神经网络训练学习时收敛速度慢及容易陷入局部极小的缺点，提高了模型的预测速度与预测精度。随着农业信息技术的不断推广，农业网络覆盖技术的不断扩大，遥感预测法得到大范围使用，通过GPS全球定位技术不仅可以进行产量预测，还可实时监控农业生产的各个环节，准确、快捷地获取相关农业信息。

③采用粗糙集理论与BP神经网络算法相结合方式对粮食产量进行预测，消除噪声数据对预测结果影响，解决粮食产量预测非线性问题，具有较高的泛化能力，较好弥补这两种方法各自缺点，相对于单一研究方法取得更精准预测结果。

④本研究不足之处在于粗糙集理论只是解决不确定性和不精确性问题的数学方法，使用有一定局限性，BP神经网络算法具有鲁棒性，易陷入局部最小，隐含层数的确定要靠经验，不能通过科学方法准确确定。因此，对于粮食产量的预测存在片面性、主观性。进一步的研究工作拟采用多种处理方法相比较方式，综合得出预测结果，力求预测结果更科学、更准确。

4 结论

本文提出基于粗糙集和BP神经网络的粮食产量预测方法，利用粗糙集理论对影响粮食产量的影响因素进行属性约简、规则提取，最终确定化肥施用量（x1）、大牲畜年底头数（x2）、粮食播种面积（x3）、有效灌溉面积（x5）和农村居民家庭平均每人全年纯收入（x7）这5个影响因素，去除3个冗余影响因素，并建立RSBP神经网络粮食产量预测模型，该组合模型消除了噪声数据，降低数据维数，简化神经网络结构，增强泛化能力，可解决粮食产量非线性问题。

[1] 苏涛,王鹏新,刘翔舸,等.基于熵值组合预测和多时相遥感的春玉米估产研究[J].农业机械学报,2011,42(1):186-192.

[2] 高倩倩,邢秀凤,姚传进.基于逐步回归分析的粮食产量影响因素研究[J].当代经济,2010,5:145-147.

[3] 徐兴梅,周翠娟,陈桂芬.基于聚类分析与时序算法的玉米测产模型[J].吉林农业大学学报,2012,34(6):688-691,704.

[4] 房丽萍,孟军.化肥施用对中国粮食产量的贡献率分析——基于主成分回归C-D生产函数模型的实证研究[J].中国农学通报,2013,29(17):156-160.

[5] 程伟,刘国璧.灰色系统理论在粮食产量预测中的应用[J].北京电子科技学院学报,2008,16(2):64-67.

[6] Pawlak Z,Slowinski R.Rough set approach to Multi-attribute decision analysis[J].European Journal of Operational Research,1994,72:443-459.

[7] 姜安龙,戚玉亮.粗糙集-BP神经网络组合方法及其应用[J].中南大学学报:自然科学版,2011,42(10):3189-3194.

[8] 钟波,肖智.一种基于粗糙集理论的组合预测方法[J].统计研究,2002(11):37-39.

[9] 姜德民,王磊,徐义田,等.基于粗糙集理论与支持向量回归的预测模型[J].统计与决策,2008(10):32-33.

[10] 郑文钟,何勇.基于粗糙集的粮食产量组合预测模型[J].农业机械学报,2005,36(11):75-78.

[11] 王国胤.Rough集理论与知识获取[M].西安:西安交通大学出版社,2001.

[12] 宋仁华,吴昊,张燕子,等.基于粗糙集和神经网络在小麦病害诊断中的应用[J].农机化研究,2012,7(7):211-214,218.

[13] 何丽红,刘金刚,文友先.基于粗糙集与支持向量机的禽蛋蛋壳无损检测[J].农业机械学报,2009,40(3):167-171.

[14] 李华华.粗糙集理论研究及其在水稻病害预测中的应用[D].北京:北京交通大学,2007.

[15] 陈桂芬,马丽,董玮,等.聚类、粗糙集与决策树的组合算法在地力评价中的应用[J].中国农业科学,2011,44(23):4833-4840.

[16] 吴玉鸣,李建霞,徐建华.中国粮食多因子灰色关联神经网络预测研究[J].华中师范大学学报:自然科学版,2002,36(4):419-423.[17] 孙健敏,吴昊,李书琴.粗糙神经网络在农业病虫害诊断中的应用[J]．农机化研究,2009(11):197-199.

[18] 叶咸,许模,廖晓超,等.遗传算法优化BP神经网络在求解水文地质参数中的应用[J].水电能源科学,2013,31(12):55-57,65.

[19] 胡英杰,裴旭明,张国民,等.基于BP神经网络的粮食颗粒群流量预测[J].机械科学与技术,2013,32(10):1538-1541.

[20] 刘建华,李天玉,付娟娟,等.基于BP和Elman神经网络的智能变电站录波启动判据算法[J].电力系统保护与控制,2014,42(5):110-115.