双转子永磁电动机有限元分析

王淑红，吕 航，武 潇，赵晓春

(太原理工大学，太原030024)

0 引 言

双转子永磁直流电机由内转子(电枢转子)和外转子(永磁体转子)组成。运行时，两个转子受到耦合场的电磁转矩为等大小反方向的相互作用转矩，使两个转子朝相反的方向旋转［1］。因此电机的固定部分不承受电磁转矩，可明显提高机身的平稳性，在船舰推进系统中有广阔应用前景［2］，针对对转结构永磁直流电动机的性能进行研究尤为重要。

文献［3］使用有限元法对传统单转子永磁直流电机进行了建模分析，简要讨论了电机结构上的各参数对性能的影响。文献［4］以抑制转矩波动为目标对传统永磁直流电机进行了优化设计，使用有限元法对优化结果进行了检验。目前对于双转子永磁直流电动机的有限元研究文献较少。本文分别就静态特性与动态特性对双转子永磁直流电动机进行了有限元分析;并采用重叠换相方法，改变控制主电路中开关管提前导通角，找到了使电磁转矩波动范围减小的最佳提前导通角。减小了稳定运行过程中的电磁转矩脉动率。

1 静态有限元模型的建立

图1 双转式永磁电动机结构

2 静态性能分析

对有限元模型计算之后能够得到静态特性，包括静磁场分布情况和一对极范围内特定激励方式下电机静转矩特性Te=f(i，θ1，θ2)，与电感特性L =f(i，θ1，θ2)。

2.1 磁场分布

图2 为两个不同相对位置处静态磁密分布图。B 相绕组中通以30 A 的正向电流，C 相绕组通相等大小的反向电流。图2(a)为初始位置处磁密分布图，可以看出12 个磁极分界线处的外转子圆钢磁密达到了高度饱和，为1.76 ～1.89 T 之间。每个磁极中心线附近的内转子齿磁密也较高，为1.63 ～1.76之间。图2(b)为两个转子相对位置为15°时磁密分布图，该时刻外转子(永磁体转子)顺时针转过约10°，内转子(电枢转子)逆时针转过约5°。由图可得磁密分布不仅整体上跟随永磁体转子转过了相应的角度，每极周期内的分布情况也存在一定的差别。

图2 不同相对位置处磁通密度分布图

2.2 静转矩特性曲线

取A 相正向绕组处于S 极的中心线处为初始位置，两个转子相对位置(θ1-θ2)的变化范围为一对极。在绕组激励不变的条件下，计算不同相对位置处数据可得到静转矩特性曲线。再依次改变激励大小可得到如图3 所示一簇静转矩特性曲线。

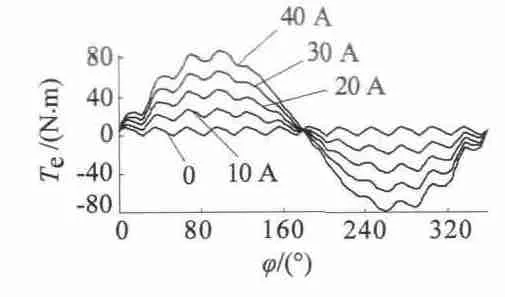
图3 静转矩特性曲线

图3 中，电流为0 时的特性曲线表示的是齿槽转矩，波动周期个数与一对极下的齿数相符，齿槽转矩是引起电机转矩脉动的主要因素。由图可得，各位置处静转矩值减去该位置处的齿槽转矩值之后基本与电流大小成正比，与永磁体励磁方式下静转矩变化规律一致。但是在少数位置处，当激磁电流超过30 A 之后，静转矩值稍低于对应理论上的正比值。这是由于该位置处磁路已经饱和，电枢反应引起每极下主磁通平均值稍有下降，因此该位置处的静转矩稍低于理论正比值。

2.3 电感特性曲线

根据不同条件下的A 相自感值可得如图4 所示的自感特性曲线簇。

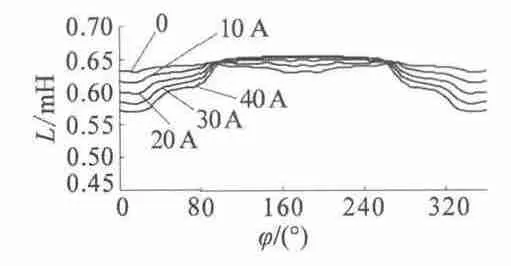
图4 自感系数变化曲线

由图4 可知，绕组中电流为0 时，自感系数随相对位置不同变化不大，绕组的自感系数近似为常数，控制系统设计时电机参数可以认为是常数。而当激磁电流变化时，特别是电流较大、转子相对位置变化时，某些相对位置处磁路饱和，绕组自感系数随转子位置不同，是近似阶梯形的曲线，并且阶梯的平顶部分都在相对位置90° ～270°的范围内，自感值也很接近。其他位置范围内的自感值随着电流值的增大而基本均匀减小，超过30 A 后随电流值变化的幅度略微降低。

根据不同条件下的A 相与B 相互感值，可得如图5 所示的互感特性曲线簇。

在数学模型研究及试验验证方面，波兰科学院[22]建立了蓄热换向流动反应器(TFRR)的一维模型的2个不同版本(①带反应器壁蓄热与②无反应器壁蓄热)，并通过大尺寸反应器上的试验数据对模型进行了验证。研究认为壁面蓄热并不会直接影响反应器内填料温度分布规律。

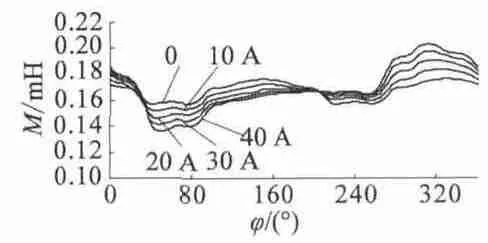
图5 互感系数变化曲线

3 动态有限元模型的建立

动态有限元模型的电机结构、绕组分相与静态模型相同，可沿用静态模型。此外，动态模型的激励形式为外接控制电路激励，并且需要将两个转子定义为独立的运动区域同时进行运算。Maxwell 2D 模块支持多个运动部分同时运算，本文在此模块下进行电机的动态有限元建模。

3.1 动态模型激励设置

动态模型的外接控制电路需要给绕组提供根据内转子和外转子的相对位置参数而周期变化的方波激励［1］，这样可保证电枢磁场与永磁体磁场等效同步，推动内转子和外转子沿着各自的方向运动。图6 为有限元计算模型中电机的主电路。通过控制主电路中的六个压控开关管，使绕组根据相对位置参数而按既定规律通断。主电路图中与各相绕组相串联支路上的电阻RA，RB，RC为相绕组电阻(三相绕组对称，RA=RB=RC=R)，电感LA，LB，LC为每相绕组的端部漏感(LA= LB= LC= Lδ)，均可通过Ansoft 软件RMxprt模块下直流电机快速建模得到:R =0.17Ω，Lδ=6.931 8 ×10-5H。图中，LWA是有限元模型A 相绕组。

图6(b)为主电路中压控开关管的控制电压检测电路。本文中设置检测电压高于0.5 V，即触发该检测表所对应的开关管导通，低于0.5 V 即关断。以A 相绕组的输入端压控开关管S1 为例，S1 所对应检测支路中脉冲信号VP1周期为60°，脉冲宽度为20°，电压下限为0，上限为1 V，上升沿位置为5°，控制信号为θ1-θ2(θ1为内转子位置变量，θ2为外转子位置变量)。相对机械位置的周期60°内，A 相正向导通范围为5° ～25°。分别设置各个开关管对应的检测支路中脉冲信号，使S2 ～S6 所对应的脉冲信号依次比前一个延后10°。采用两相同时通电方式，若A+C-表示A 相正向和C 相反向导通的状态，则一周期内绕组导通状态依次为A +C -，B +C-，B+A-，C+A-，C+B-，A+B-。

图6 使用Maxwell 编辑的外电路

3.2 运动区域设置

相对于单转子旋转电机，双转子直流电动机的机械运动部分的设置较特殊，对双转子电机的动态性能有限元计算论文较少。对本文所研究的双转子直流电动机而言，两个转子的机械运动部分是各自独立的，应为两个转子分别设置运动求解区域(Band)。建立能恰好包含内转子的面域，设为Band1;建立恰好包含外转子的面域，设为Band2，如图7 所示(图中阴影部分为各自的Band 区域)。

图7 运动区域设置图

运动区域内物体的运动方式都设定为绕Z 轴的旋转运动，并分别载入计算所得的转动惯量，内转子转动惯量为0.064 6 kg·m2，外转子转动惯量为0.034 1 kg·m2。

4 动态性能分析

双转子永磁直流电动机动态性能包括:起动过程及稳定运行时绕组电流、内转子和外转子各自的电磁转矩、转速随时间变化曲线。

4.1 电流变化曲线

从电枢绕组的电流方程、电压平衡方程来看，对转式永磁直流电动机等效电路与传统无刷永磁直流电动机一致，可借助传统单转子电机的电路平衡关系来分析该电机电枢电流。

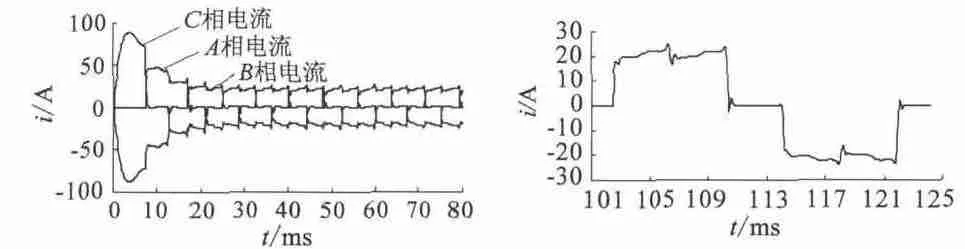
图8 电流曲线

在三相六状态工作方式下，每时刻均为两相绕组导通，另一相为续流状态或者完全关断状态，如图8(a)所示。若取一相绕组的一次续流过程和完全关断过程为一个换相周期，则电机运行过程可完全由三相的换相周期轮流组成。以A+C-状态转换至B+C-状态的换相周期为例，此换相周期可分为A 相续流过程t1和A 相完全关断过程t2组成。根据续流过程等效电路可得续流过程中电流方程式如下［5］:

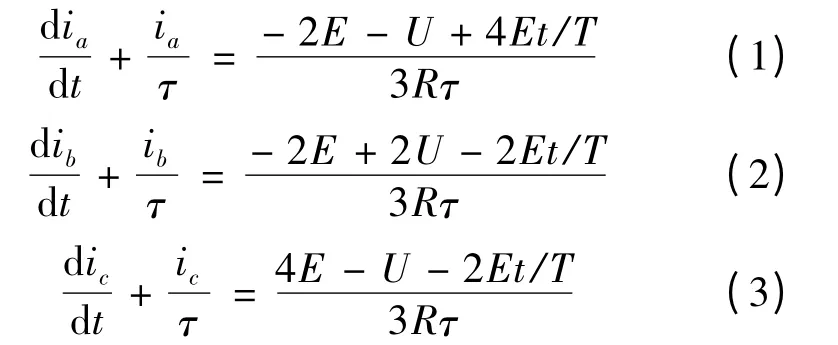
式中:τ 为相绕组电磁时间常数;R 为相绕组电阻;I0为换相过程A 相初始电流;U 为输入到逆变器的直流电源电压;E 为相绕组等效反电势幅值。有限元计算所得电机稳定运行时相绕组反电势波形如图9所示，图中曲线为相对转速稳定在430 r/min 时一个电周期内相绕组反电势波形。曲线在齿槽效应影响下具有多次波动。为方便公式计算，将反电势波形等效为规则120°梯形波。上式中，反电势幅值E为等效梯形波幅值，不能取原波形的波动峰值。

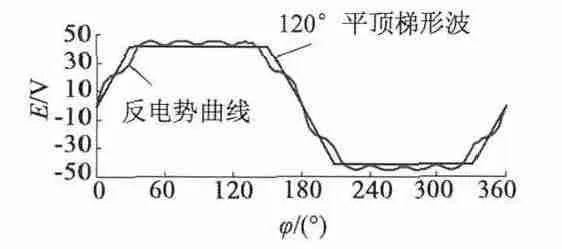
图9 相绕组反电势波形

根据式(1)至式(3)，令初始条件:ia(0)=I0，ic(0)= -I0，ib(0)=0。求取微分方程，可得A 相绕组电流降为零，所需的时间t1与t1时刻结束时B 相和C 相电流值表达式:

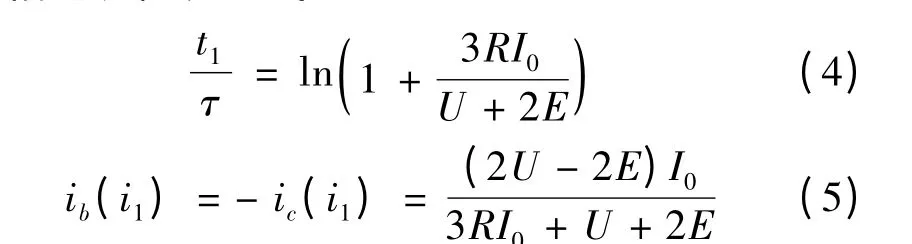
由式(4)、式(5)可得t1=0.25 ms，ib(i1)=16.9 A;与图4 中的数据t1=0.2 ms，ib(i1)=17.2 A 基本吻合。其中t1的差别是由于时间段t1很短暂且与Maxwell 中的计算步长0.2 ms 相仿，因而等效为一个步长。由计算结果可知，由于电流变化率的不同，绕组由导通到电流下降至零的时间很短暂，而此时新导通相的电流尚未上升到平均导通电流［6］，因此续流过程的三相电流值大小均会小于其他时间的电流值。

4.2 电磁转矩曲线

转矩脉动率有以下定义［7］:

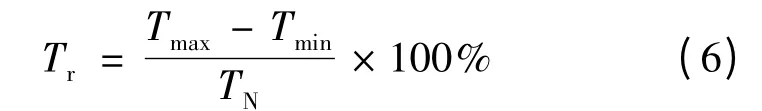
式中:Tmax为电磁转矩最大值;Tmin为电磁转矩最小值;TN为电磁转矩稳定运行的平均值。

电机起动到稳定运行过程中，两个转子所受的电磁转矩曲线如图10(a)所示。

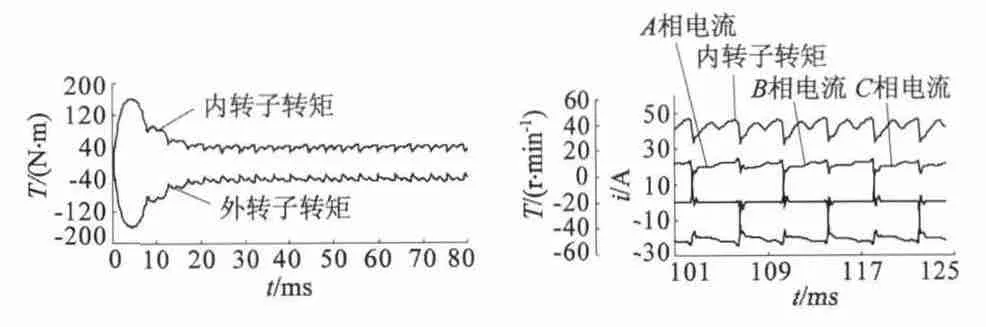
图10 电磁转矩曲线

由图10 可知，内转子与外转子所受电磁转矩时刻大小相等方向相反。根据式(6)计算可得稳定运行过程的转矩脉动率Tr=43.1%，每电周期内有12 次波动，对应于一对极范围下的12 组齿槽;其中有6次达到最小值并且均出现在关断相的续流过程中。

稳定运行过程中，一个电周期内绕组电流与内转子所受电磁转矩的曲线如图10(b)所示。电磁转矩的最小值均出现在续流过程中。根据电流曲线的分析结论可知，续流过程中续流相电流已降为零，新导通相电流还未增加至稳定值，换相过程中电磁转矩会减小［8］。并且正在换相的两相绕组也正处于气隙磁密较小的位置，因而电枢绕组所受的总电磁转矩降至转矩脉动的最低值。

4.3 转速曲线

电机起动到稳定过程中，两个转子的转速曲线如图11 所示。在30 ms 时刻到达稳定转速，内转子为150 r/min，外转子为280 r/min。两个转子稳定转速的比值为0.536，转动惯量比值为1.894，两者之积为1.015≈1。因此两个转子负载转矩相同的情况下，稳定转速的大小与各自的转动惯量基本成反比。

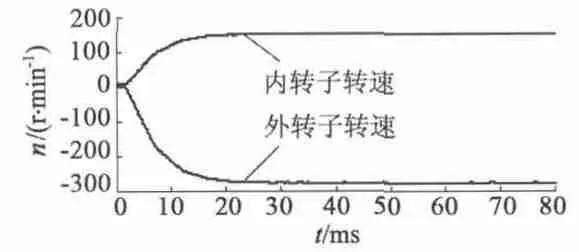
图11 转速曲线

5 转矩脉动抑制

由图10(b)的电磁转矩分析结果可得，在绕组换相的续流过程中，所引起的转矩波动较之齿槽转矩波动影响更大。采取措施减小换相转矩脉动将明显提高转矩整体平稳性。而选择适当的提前导通角度［9］，使续流绕组与将要导通的绕组重叠导通，可以补偿续流过程中的电流值下降，减小凹下的电磁转矩波动［10］。如果提前导通角度过大，则会引起新的转矩波动［11］，因此必须在合适的提前导通角下才能有效减小转矩波动。文献［12］提出了针对不同换相过程中提前导通角(时间)的计算方法。在4E＞U 的条件下，电机运行在高速段，此过程中换相时间可表示:

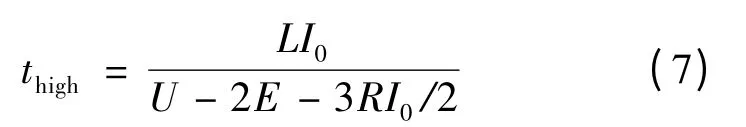
式中:L 为绕组等效电感，等于相绕组自感与绕组间互感之差。由式(7)计算出换相区间时间并换算为角度，该值的一半为最佳提前换相角，为2.2°。在有限元软件Maxwell 2D 环境下可通过改变开关管控制回路来模拟换相绕组提前导通。将控制回路中每个脉冲信号的上升沿根据相应的提前导通角前移并维持下降沿不变，可改变各脉冲信号所对应的MOS 管导通范围，实现绕组提前导通。通过比较2.2°左右的不同提前导通角下有限元分析结果发现，提前导通2°时电磁转矩波动最小。在这种方案下压控开关管S1 的导通区间为3°～25°，S2 ～S6 各自的导通区间依次比前一个延后10°。以A+C-状态转换至B+C-状态的换相过程为例，将出现23°～25°的三相同时导通区间，这就形成了重叠换相。图12 为有限元计算所得不采用提前导通与采用提前导通(提前导通角为2°)时两个转子的电磁转矩曲线比较图，由图12 可得稳定运行过程中电磁转矩脉动率Tr=27.9%，与不采用重叠换相相比减小了15.2%。

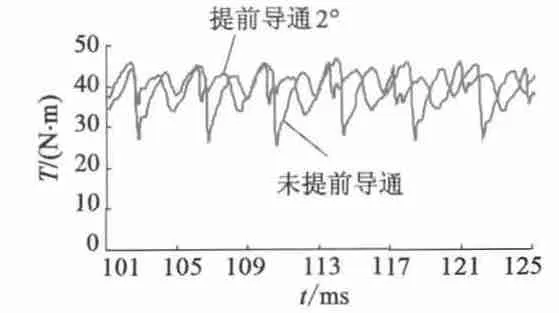
图12 电磁转矩曲线比较图

6 结 语

本文建立了双转子永磁直流电动机的电磁场有限元模型，使用有限元分析软件Maxwell 2D 模块分别对电机静态性能和动态性能进行了分析。通过静态仿真绘制了磁场分布与静态特性曲线，为优化电机结构参数与分析电机特性提供了理论依据。通过动态仿真实验得到了各参数的运行规律，并得到了减小电磁转矩波动的最佳提前导通角，为电机控制策略的优化提供了基础。

［1］ 张世勤，邱建琪. 双转式永磁无刷直流电动机的建模与仿真［J］.中国电机工程学报，2004，24(12):176 -181.

［2］ 孙希通，王育才.双转式永磁无刷直流电动机系统建模与仿真［J］.电机技术，2009(3):1 -4.

［3］ 王瑞，高尚.永磁无刷直流电机电磁场有限元分析［J］.电子技术，2011(5):69 -71.

［4］ 连军强，谢顺依.基于有限元的永磁无刷直流电机转矩优化设计［J］.电机与控制应用，2011，38(12):7 -12.

［5］ 谭建成.永磁无刷直流电机技术［M］.北京:机械工业出版社，2011.

［6］ 包向华，章跃进.无刷直流电动机换相转矩脉动的分析和削弱方法［J］.微特电机，2007，35(2):14 -17.

［7］ 孙建忠，白凤仙.特种电机及其控制［M］.北京:中国水利水电出版社，2005.

［8］ 李怀兵，丑武胜.换相期间无刷直流电机转矩脉动的抑制策略［J］.电机与控制应用，2011，38(11):20 -24.

［9］ 刘会飞，王淑红.无刷直流电动机转矩脉动的抑制［J］.电力学报，2006，21(2):157 -159.

［10］ YOSHIDAM M. Noise reduction by torque ripple suppression in brushless DC motor［C］//Proceedings Form PESC Record.1988:1397 -1401.

［11］ 王淑红，熊光煜.无刷直流电机换相转矩脉动减小及动态仿真［J］.电机与控制学报，2008，12(2):169 -173.

［12］ 罗宏浩，吴峻.永磁无刷直流电机换相控制研究［J］. 中国电机工程学报，2008，28(24):108 -112.