基于气隙磁场测定的永磁球形电动机位置检测方法研究

马 姗，李国丽，钱 喆，王群京，过希文，刘阿娟

(1.安徽大学，合肥230601;2.安徽安纳达钛业股份有限公司，铜陵240024)

0 引 言

多自由度运动系统有着广泛的运用，比如机器人机械臂、红外与激光跟踪系统、自动化制造等。当前的多自由度运动系统由单个自由度驱动和传动机构实现，系统庞大、复杂。由于受转动惯量、间隙、非线性摩擦和齿轮弹性形变等因素影响，难以获得高的动态性能。随着对多自由度执行机构动态和稳态性能的要求日益提高，科研人员积极参与研制具有多自由度运动功能的精密执行器。Lee K M 等人提出了变磁阻型球形步进电动机［1］，Wang J，Jewell G W 提出了两自由度电机［2-3］，Kahlen K 和Week E M等人研发了一种三自由度永磁球形电动机［4-5］。国内也积极推进多自由度电动机的研究。比如，苏仲飞、刘昌旭等人设计出无刷直流球形电动机［6］;黄声华等人提出双馈感应球形电动机［7-8］;程树康、蔡鹤皋等人设计研制了非球形结构的正交圆柱结构三自由度电机［9-10］，夏长亮、李洪凤、郭辰等提出了基于Halbach 阵列的永磁球形电动机［11-13］。

为了达到精确控制多自由度电机的目的，需要实时掌握转子的位置。文献［14］中，Lee K M 提出了采用一套由两个半圆形滑轨支架、固定输出轴和3 个旋转编码器组成的滑轨支架测量系统来检测转子位置的方法。该方法引入了转子与导轨相连接产生的摩擦，影响转子的定位精度。Chirikjian G S 等人提出了基于光电传感器的转子位置检测方法［15-16］;王群京、钱喆等人提出了基于机器视觉的永磁球形步进电动机的转子位置检测方法［17］，这些方法虽然克服了接触式测量带来的摩擦，但测量原理和结构复杂，而且难以实现实时位置检测。

本文提出了基于永磁体作磁源、通过三个固定检测点检测到的三维磁感应强度数据来计算转子位置的方法。

1 检测基本原理

置于转轴上的永磁体随转轴转动时，永磁体将在其周围建立一个稳态磁场。而转轴相对于参考坐标系的方位信息，包含在空间固定点的磁感应强度数据中。图1 展示了坐标系中一个长度l，半径α，均匀轴向磁化且剩余磁感应强度为M0的圆柱永磁体。永磁体中心点Pm至坐标原点的距离为Lm。永磁体所在轴线与z 轴的夹角以及轴线在xoy 平面上的投影与x 轴的夹角分别为θ 与φ。z 轴上PS点的坐标为(0，0，Ls)，将PS点的磁感应强度B 分解为平行转轴方向的Bl和垂直转轴方向的Bρ，则PS点x 轴方向的磁感应强度Bx和y 轴方向的磁感应强度By与Bl和Bρ的关系可由下式表达:

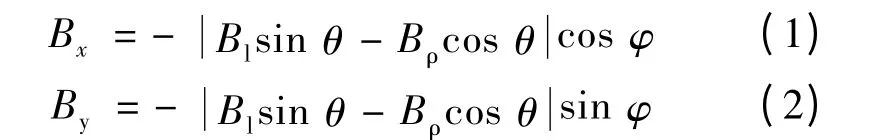
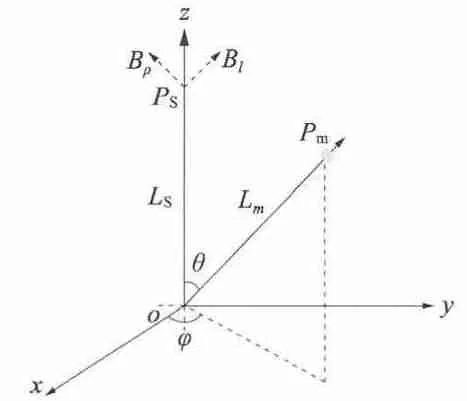
图1 阐述永磁体位置的坐标系

位于永磁体所在转轴上的P 点在xyz 坐标系的坐标P(x，y，z)可用式(3)表述。

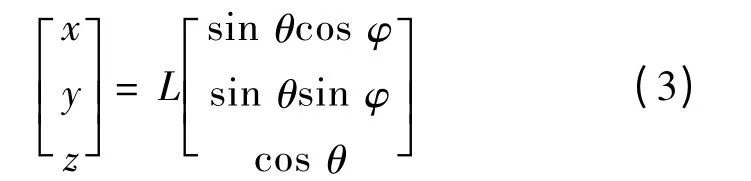
式中:L 为P 点到原点的距离。显然，P 点坐标P(x，y，z)由θ，φ 唯一决定。

式(1)和式(2)提供了求解角度φ 的方法。在PS点放置三维磁感应强度传感器S，测得磁感应强度Bx，By，Bz。则φ 可由下式求得:

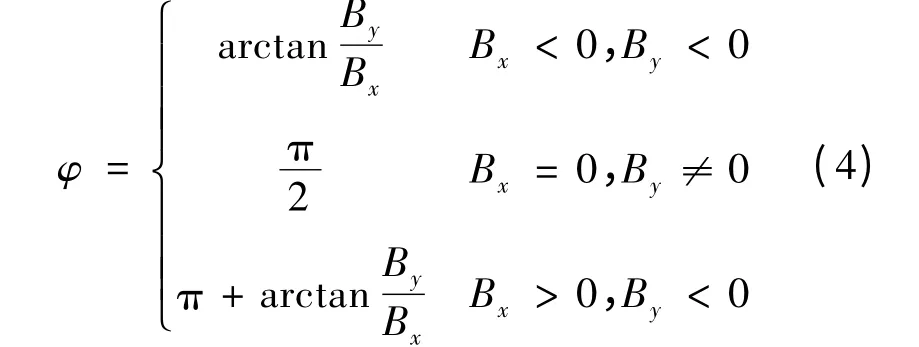
当Ls取恰当值时，B 值与θ 成单值函数关系，即B=f(θ)为单调函数，θ∈［0，θ0］。当S 测得点磁感应强度为B^时，确定Bk+1＜B^＜Bk(k∈［1，n -1］)。则此时转轴与z 轴的夹角θ^可由下式求得:

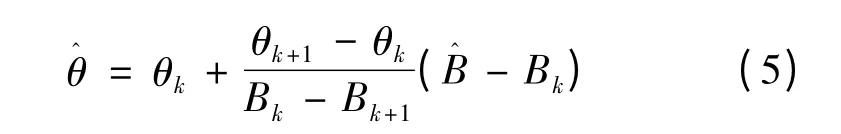
式中:θk∈［0，θ0］，Bk=f(θk)(k =1，2，…，n -1)。θ^的精度取决于n 的大小和Bk的精确度。

根据式(4)和式(5)，求得θ 和φ，确定球形电动机转子位置。据此，下文构思设计了球形电动机的位置检测系统。

1.1 球形电动机位置检测系统设计

图2 为是本文研究的球形电动机实体模型，详细参数如表1 所示。图3 和图4 展示了检测系统的设计理念，三维磁感应强度传感器分别置于x1y1z1，x2y2z2，x3y3z3坐标系中的z1，z2，z3轴上。检测点到原点O 的距离为Ls。x1y1z1坐标系由XYZ 坐标系逆时针绕X 轴旋转α 角得到;XYZ 坐标系绕Z 轴逆时针旋转120°后再绕x 轴逆时针旋转α 角得到x2y2z2坐标系;x3y3z3坐标系由XYZ 坐标系绕Z 轴逆时针旋转240°后再绕x 轴逆时针旋转α 角得到。

图2 球形电动机实体模型

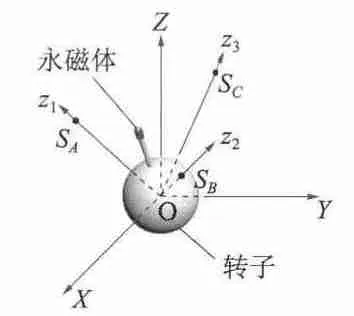
图3 检测系统立体示意图

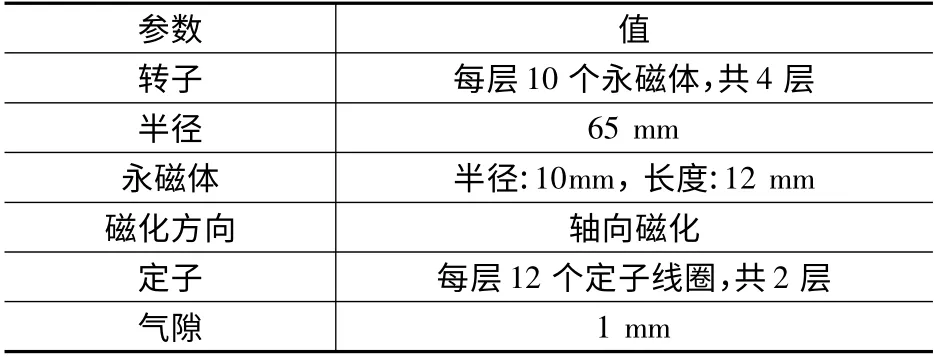
表1 永磁球形电动机参数

将检测区域划分为图4 中A，B，C 三块区域。转轴运动至A 区域时，由SA负责检测转轴上P 点位于x1y1z1坐标系中的位置P(x1，y1，z1)。通过坐标转移变换可得到P 点在绝对参考坐标系XYZ 中的坐标。式(6)给出了P(X，Y，Z)的求解方法。

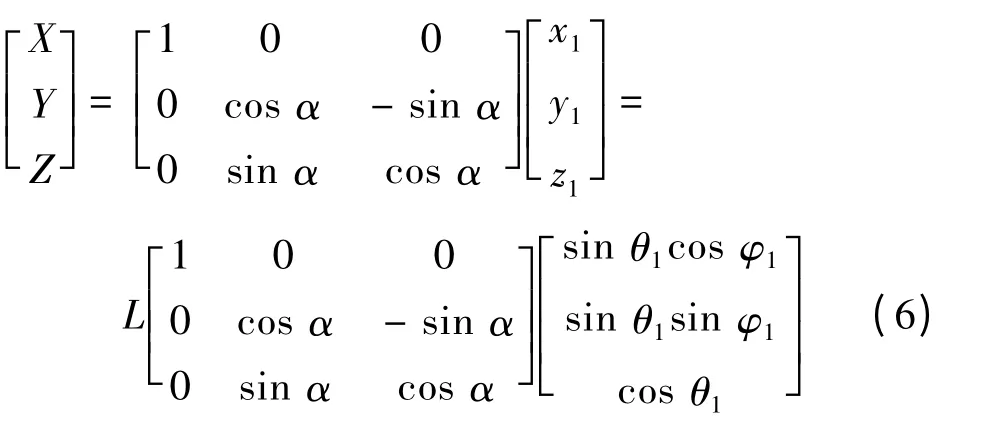
式中:L 为转轴上P 点到原点O 的距离;θ1和φ1分别为球形电动机转轴与z1轴的夹角和转轴在x1y1z1平面内的投影与x1轴的夹角。

同理，转轴运动至区域B 时点P 在XYZ 坐标系内的坐标可由下式求得:

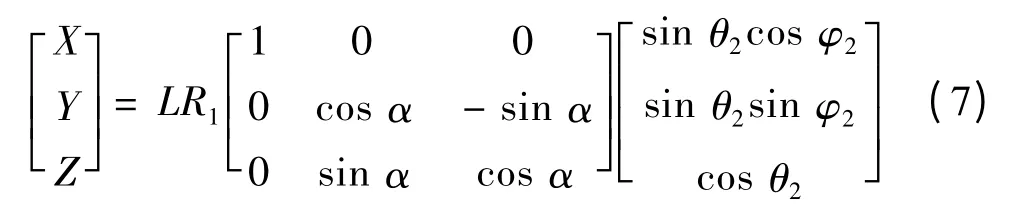
转轴运动至区域C 时P 点在XYZ 坐标系内的坐标由式(8)求得。θ3和φ3分别为球形电动机转轴与z3轴的夹角和转轴在x3y3z3平面内的投影与x3轴的夹角。

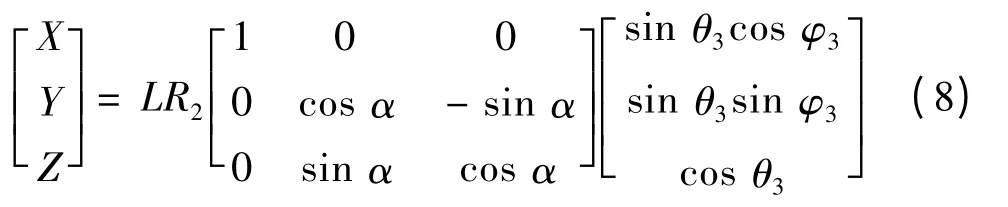
1.2 圆柱永磁体产生的磁感应强度计算

预知PS点的磁感应强度B 是前文提出算法实现的前提，而且掌握了解PS点磁感应强度Bx和By的变化范围对角θ0的大小及三维磁感应强度传感器的选择至关重要。点的磁感应强度可以通过分布式磁偶极子法按照式(9)～式(12)求得［18］。

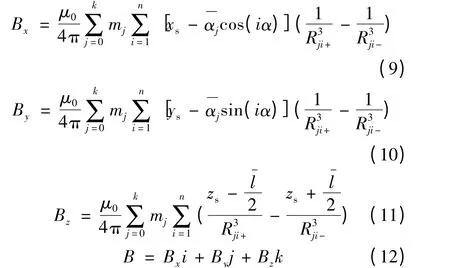
上述公式中，μ0是真空磁导率，k 和n 分别为分布式磁偶极法模拟的永磁体的圆周对数目以及每对圆周上含有的磁偶极子对数目，mj是位于第j 个圆周上的磁偶极子的磁偶极矩。γ 角为相邻的两个磁偶极子对应的圆心角。为第j 个圆周的半径，且

1.3 检测点磁感应强度计算分析

永磁体运动在A 区域内SA检测的磁感应强度变化情况与永磁体运动在B、C 区域SB、SC感知的磁感应强度变化情况完全一样。因此可仅分析运动于区域A 内SA检测的磁感应强度变化情况。

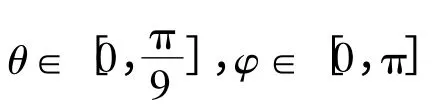
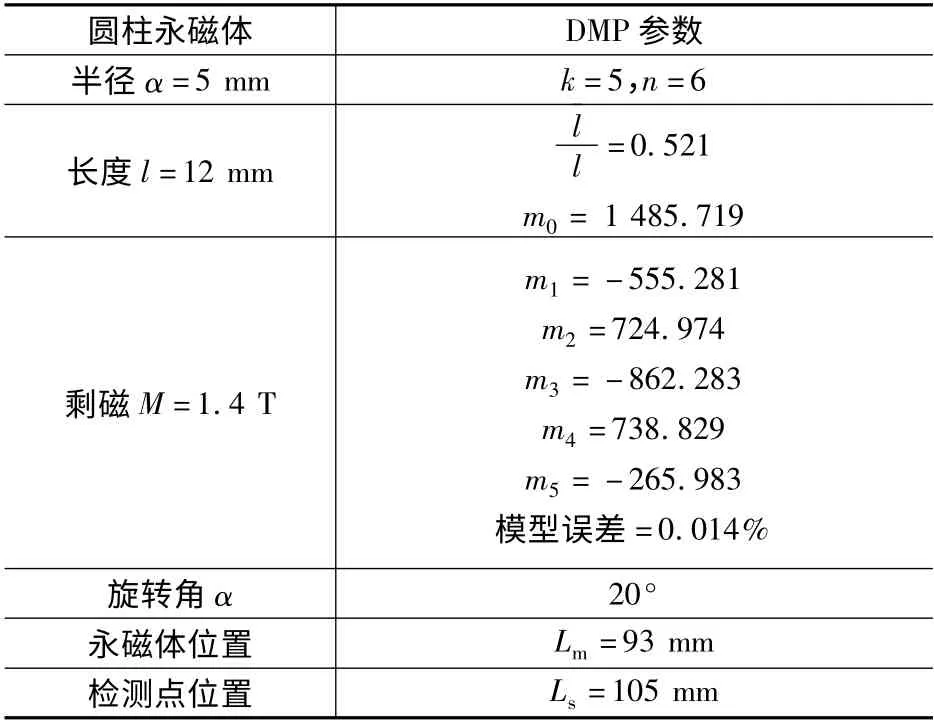
表2 磁源及固定检测点参数

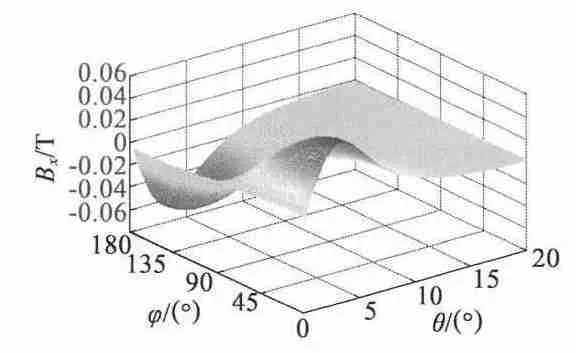
图5 x 方向磁感应强度

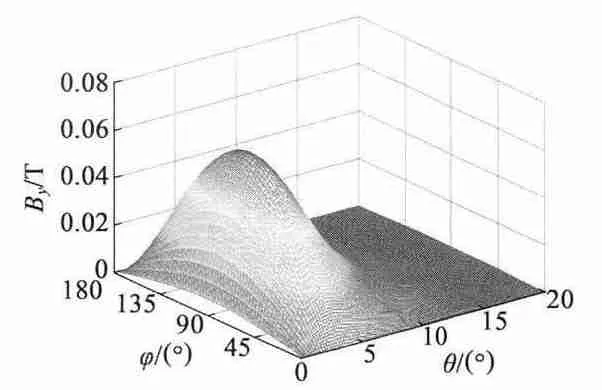
图6 y 方向磁感应强度

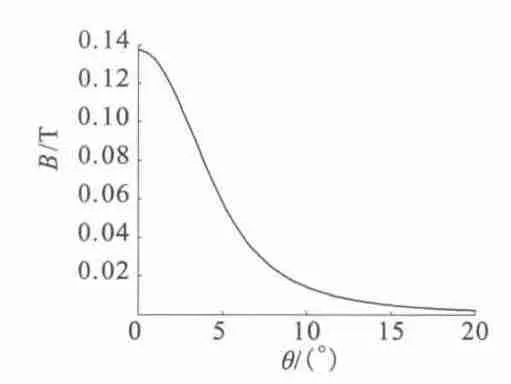
图7 随θ 变化的磁感应强度B

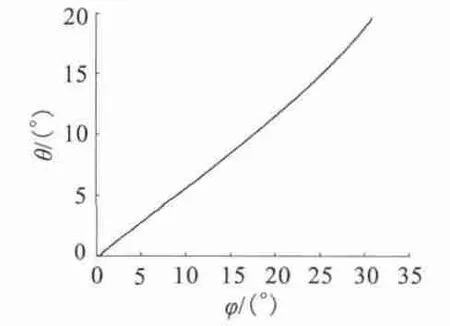
图8 φ1 与θ1 的函数关系

1.4 转子永磁体以及通电线圈对检测点磁感应强度影响分析

转子永磁体以及通电线圈对检测点的磁感应强度影响会降低位置检测的精度。因此，选择检测点位置时应以尽量减少转子永磁体和通电线圈对检测点磁感应强度影响为原则。图9 是用MagNet 建立的本文研究的球形电动机模型，基于此模型分析转子永磁体以及通电线圈对本文选取的检测点磁感应强度影响。

图9 球形电动机仿真模型

转轴与Z 轴重合时记α 角为0°，转子绕X 轴逆时针旋转记为正，反之为负。图10 刻画了α 角变化范围为［-20°，20°］时，固定检测点A 的由转子永磁体产生的磁感应强度变化情况。由于将整个检测区域等分为三个部分，所以当转子顺时针旋转时，虽检测点A 受到的来自转子永磁体的磁感应强度影响较大，但此时检测点B 或C 检测到的磁源永磁体产生的磁感应强度大于前者，转子的位置检测通过B 或C获得。转子逆时针旋转时，从图中可以看出，转子永磁体对检测点的磁场影响在5 ×10-4T 以下，而此时磁源永磁体作用于检测点A 的磁感应强度较大，转子永磁体对检测结果的准确度有微弱的影响。

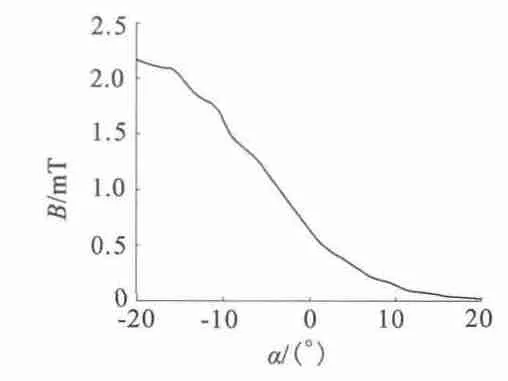
图10 转子永磁体产生的磁感应强度

图11 分析的是一个通以电流1 A，1 200 匝的线圈，在检测点所在圆周产生的磁感应强度。从图中可以看出，通电线圈在圆周上产生的磁感应强度在1 ×10-4T 左右，对检测点的影响可以忽略。由于定子线圈与检测点是相对静止的，将检测点选择在过两个定子线圈中间线的平面与圆周的交点处可以最大限度降低通电线圈对检测点磁感应强度的影响。

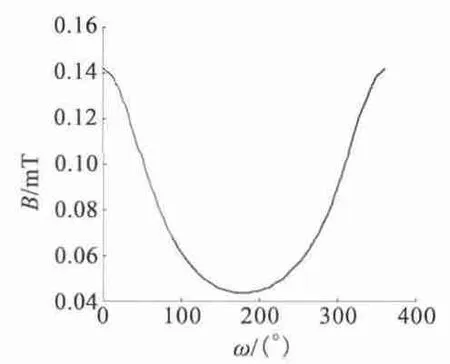
图11 通电线圈产生的磁感应强度

2 仿真分析

本文选取了转轴运动在A 区域内的不同位置的P 点的一系列坐标P(Xi，Yi，Zi)(L 取100 mm)，通过MagNet 软件，求解出PS点在转轴上P 点处于这些位置时的磁感应强度Bxi、Byi以及Bi。再通过公式求解出相应的点P 的坐标P(，，)。图12和图13 展示了三维和二维的定位结果。图14 展示了P 在不同位置时的定位误差。仿真结果表明，转轴运动在A 区域内时，定位误差在2 mm 以内。另外，前20 个采样点的定位误差比剩余采样点的小，这是由于前者这些点对应的转轴与z1轴的夹角θ较后者小;前者采样点对应的检测点磁感应强度较强，计算结果精确度高。提高θ 角较大时的定位精度以及扩大检测区间范围，取决三维磁感应强度传感器测量下限的提高。

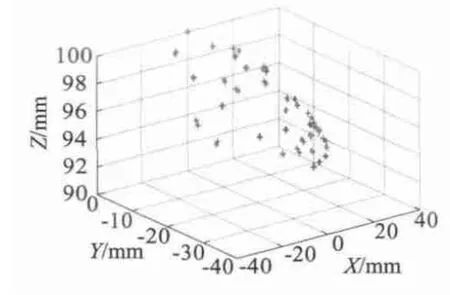
图12 三维空间位置

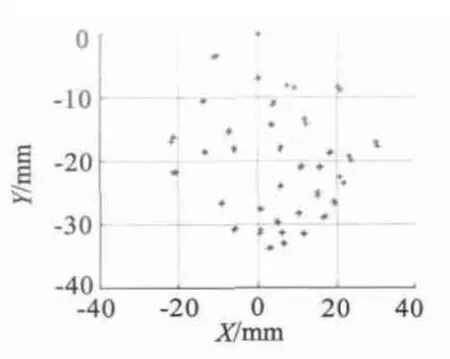
图13 二维空间位置

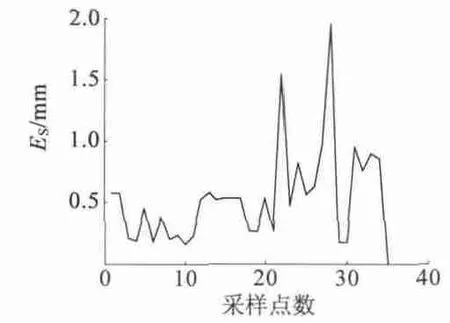
图14 位置误差

3 结 语

本文用分布式磁偶极子法分析了磁源永磁体随转轴在检测区域转动时空间固定点的磁感应强度变化情况。以此为基础，通过固定检测点的三个正交方向的磁感应强度数据的处理计算，获得转轴位于相对坐标系中的方位信息，再通过坐标转移变换，得到球形电动机转轴位于绝对坐标系中的位置。仿真结果表明了该方法的可行性。本文提出的非接触式检测方法能够实现实时二自由度位置检测，为以后进一步研究基于磁场的三自由度位置检测提供了参考。

［1］ LEE K M，VACHTSEVANOS G，KWAN C. Development of a spherical stepper wrist motor［J］.Journal of Intelligent and Robotic Systems，1988，1(3):225 -242.

［2］ WANG J，JEWELL G W，HOWE D. A novel spherical actuator:design and control［J］.IEEE Transactions on Magnetics，1997，33(5):4209 -4211.

［3］ WANG J，JEWELL G W，HOWE D.Modelling of a novel spherical permanent magnet actuator［C］//Proceedings of IEEE International Conference on Robotics and Automation.1997:1190 -1195.

［4］ WEEK E M，REIARTZ T，HENNERBERGER G，et al.Design of a spherical motor with three degrees of freedom［J］.CIRP Annals-Manufacturing Technology，2000，49(1):289 -294.

［5］ KAHLEN K，VOSS I，PRIEBE C，et al.Torque control of a spherical machine with variable pole pitch［J］. IEEE Transactions on Power Electronics，2004，19(6):1628 -1634.

［6］ 苏仲飞，刘昌旭，韦平顺，等.机器人关节用三自由度球形直流伺服电机［J］.高技术通讯，1994(8):16 -18.

［7］ 黄声华，陶醒世，林金铭. 三维电动机的电磁模型［J］. 电工技术学报，1994，9(4):17 -20.

［8］ 黄声华，陶醒世，林金铭. 三维电动机力学模型及解耦控制［J］. 电工技术学报，1996，11(1):12 -16.

［9］ 程树康，崔淑梅，刘宝廷，等.正交圆柱结构双气隙共磁钢三自由度电动机初探［J］.中国电机工程学报，1997，17(5):7 -11.

［10］ 崔淑梅，柴风，程树康.正交圆柱结构三维电动机磁系统分析［J］.微特电机，1999，27(6):26 -28.

［11］ LI H，XIA C，SHI T.Spherical harmonic analysis of a novel Halbach array PM spherical motor［C］//IEEE International Conference on Robotics and Biomimetics.2007:2085 -2089.

［12］ LI H，XIA C，SHI T.3 -D magnetic field and torque analysis of a novel Halbach array permanent - magnet spherical motor［J］.IEEE Transactions on Magnetics，2008，44(8):2016 -2020.

［13］ XIA C，SONG P，LI H，et al. Research on torque calculation method of permanent-magnet spherical motor based on the finite-element method［J］. IEEE Transactions on Magnetics，2009，45(4):2015 -2022.

［14］ LEE K M，KWAN C K.Design concept developpment of a spherical stepper for robotic applications［J］.IEEE Transactions on Robotics and Automation，1991，7(1):175 -181.

［15］ STEIN D，CHIRIKJIAN G S.Experiments in the commutation and motion planning of a spherical stepper motor［C］//ASME Design Engineering Technical Conferences and Computers and Information in Engineering Conference.2000:1 -7.

［16］ STEIN D，SCHEINERMAN E R，CHIRIKJIAN G S.Mathematical models of binary spherecal - motion encoders［J］. IEEE/ASME Transactions on Mechatronics，2003，8(2):234 -244.

［17］ 王群京，钱喆，李争，等. 基于机器视觉的永磁球形步进电动机转子位置检测方法［J］.中国电机工程学报，2008，28(36):73 -79.

［18］ SON H，LEE K M. Distributed multipole models for design and control of PM actuators and sensors［J］. IEEE/ASME Transactions on Mechatronics，2008，13(2):228 -238.