EEMD联合AOK-TFR提取车辆微多普勒特征
张万君,牛敏杰,吴晓颖
(装甲兵工程学院兵器工程系,北京100072)
目标或者目标的组成部件存在平动以外的振动、转动等微动时,会对雷达回波信号进行频率或幅度调制并产生多普勒边带,即微多普勒效应(micro-Doppler effect)[1]。微多普勒效应可以视为目标或者部件微动和主体运动相互作用的结果,雷达信号经过目标微动(如直升机叶片的转动、人的体动、车体振动等)的调制,产生相对稳定的微多普勒边带特征,准确提取这种微多普勒特征对探测和识别目标具有重要潜在价值。国外对利用微多普勒效应识别地面车辆的研究较早,G.E.Smith 等人[2]在研究轮式车辆和履带车辆识别时,成功引入了语音识别技术。Thales公司开发了基于微多普勒特征的小型跟踪雷达,对单兵、坦克等具有很高识别率[3]。在回波特征提取方法上,时频分析法成为主要手段,复杂微动特征的提取通常需要利用回波多分量瞬时频率特征,经验模态分解法(Empirical Mode Decomposition,EMD)得到广泛应用[4-5]。
EMD尽管能分解多分量回波信号,但由于车辆雷达回波存在地杂波等噪声,会出现模态混叠问题,Hilbert谱也会被噪声严重污染。基于此,本文通过建立地面车辆振动和车轮转动回波模型,提出了用总体经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)联合自适应最优核时频分布(Adaptive Optimal Kernel Time-Frequency Distribution,AOK-TFR)提取运动车辆微多普勒特征,并进行了低信噪比下多分量信号回波仿真,结果表明:该方法有效克服了EMD分解产生的模型混叠问题,并且成功抑制了噪声污染,得到了时频分辨率更高的车辆微多普勒时频像。
1 运动车辆的微动回波模型
高频状态下,车辆微动回波可以看作是若干点散射体的叠加,微动建模时可从点目标入手获得车辆微动回波模型。
1.1 车体振动回波模型
图1为简化的车体振动回波模型,该模型基于以下假设:在高频区远场条件下,将入射波近似视为平面波,车辆为电大尺寸目标,考察时间范围内雷达视线角不变。
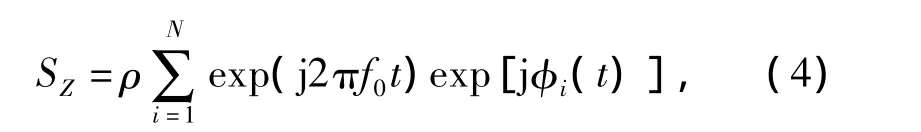
式中:φi(t)为各散射点回波调制相位。
1.2 车轮转动回波模型
车轮转动对回波调制分析方法和车体振动类似,其回波模型如图2所示。ω0。在t时刻,散射点P到雷达距离为
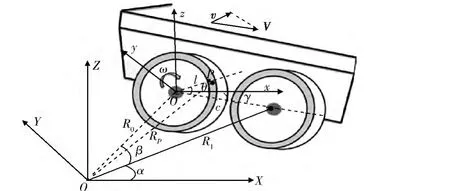
图2 车轮转动回波模型
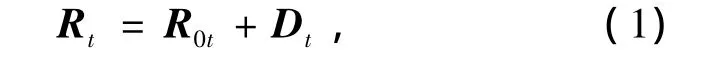
则P点到雷达的距离表达式为
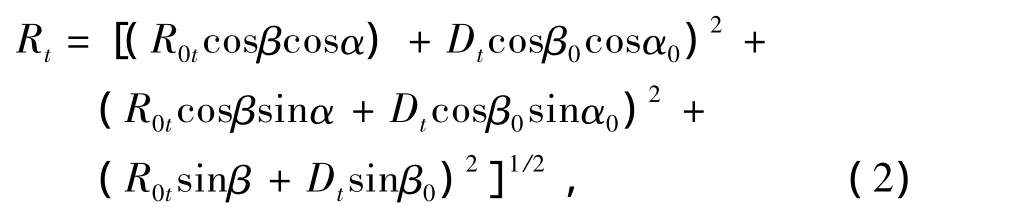
式中:R0t为 t时刻参考坐标系与雷达距离;Dt=Dvsinω0t,为t时刻车体表面振动振幅。
P点的回波信号可以表示为
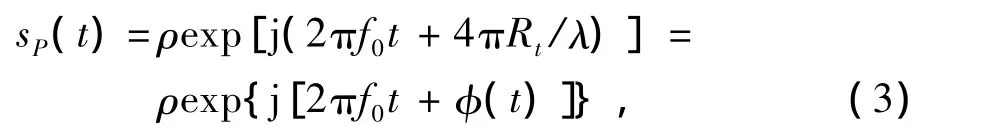
式中:ρ为散射系数;φ(t)为调制相位;λ为雷达波长。
假设振动目标由N个散射点组成,则振动回波信号为
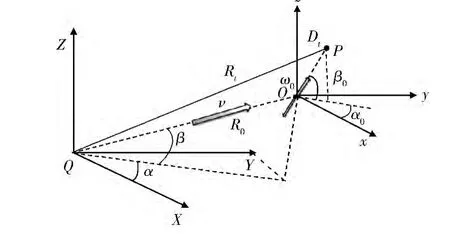
图1 车体振动回波模型
雷达坐标系是以Q为中心的Q(X,Y,Z);参考坐标系是以O为中心的O(x,y,z),与雷达坐标系平行且随车平动,O与雷达初始距离为R0,车辆相对雷达速度为V。设雷达发射单频连续波信号:s(t)=exp(j2πf0),其中f0为载频。雷达视线角方向向量:n=(cosβcosα,cosβsinα,sinβ)T。取车体振动散射点P,在参考坐标系中作简谐振动,振动方向方位角为α0,俯仰角为β0,振幅为D0,角频率为
车轮半径为l,散射点P在圆周上,车体运动方向与x轴的夹角为γ。t时刻时,P点转角为θt=θ+ωt,其中,θ为初始转角,ω为转动角速度。散射点 P在参考 坐标系 中的 坐 标为 (cosθtcosγ,-l cosθtsinγ,l sinθt),参考坐标系到雷达的距离为Rt=R0+vt,O点相对于雷达的径向速度v=cos(α+γ)·|V|。车轮间距为d,这里考虑6轮情况,R1和R2分别为其他车轮相对雷达的初始距离,由图2所示三角关系可得
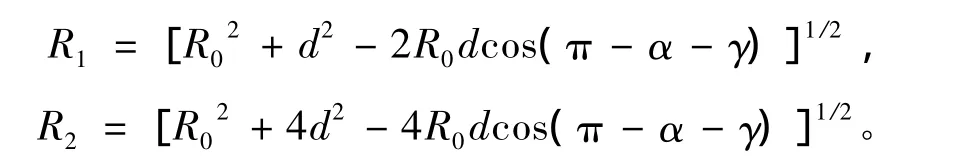
t时刻P点到雷达的距离为
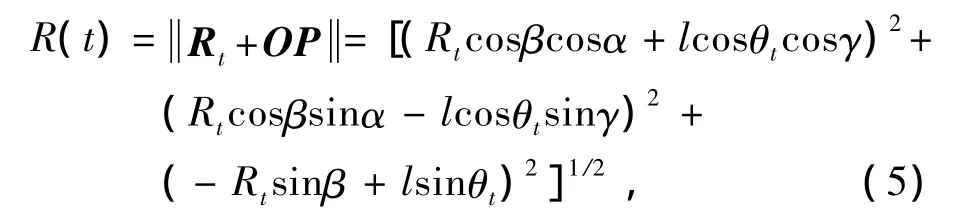
则散射点P的回波信号为
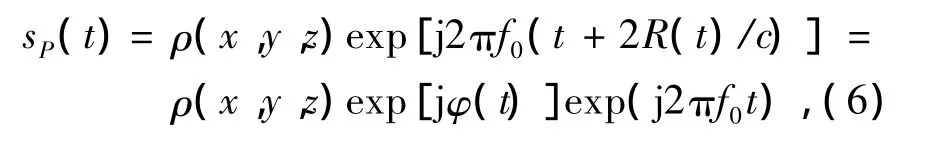
式中:c为电磁波传播速度。将车轮回波散射看作N个散射点沿圆周方向积分,得到车轮转动回波为
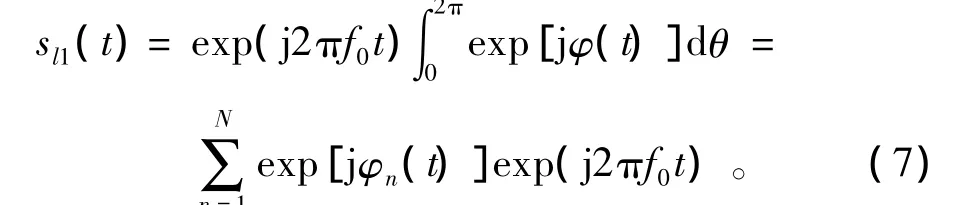
同理,可得其他两车轮散射回波sl2(t)、sl3(t),总的车轮散射回波sl=sl1+sl2+sl3。
2 运动车辆微动特征解析方法
由车辆微动雷达回波模型得到了调制回波,但在实际微动回波接收时还会有噪声干扰,这种非平稳、非线性多分量微动回波已不能用简单的频谱分析。EMD分解成为解决车辆微动复合信号的主要工具,但模态分量和Hilbert谱易被地杂波等强噪声干扰,故本文提出利用加入高斯白噪声平滑信号的EEMD[6]联合AOK-TFR的方法,得到运动车辆微多普勒的稳定、高分辨率时频像,具体算法如图3所示。
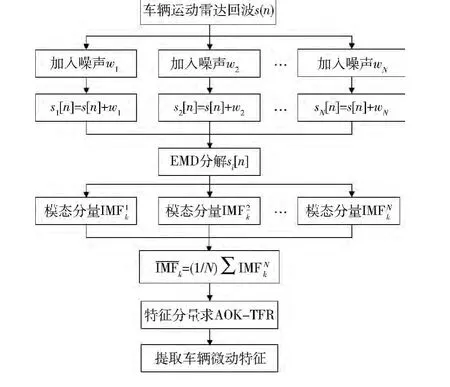
图3 运动车辆微动特征解析算法
EEMD分解时对车辆回波加入了高斯白噪声,噪声干扰将充斥在各个频段,使得回波在分解过程中表现出尺度的连续性,相当于对回波进行了平滑操作,地杂波等干扰将包含在噪声中,通过对模态分量的多次平均运算后,噪声被逐渐剔除,在很大程度上抑制了回波噪声和模态混叠问题。
在对分解后的微动特征分量进行时频分析时,短时傅里叶变换等传统加窗时频分析方法窗口一旦选定,则不能随微动回波变化而改变[7]。AOK-TFR是一种二次型时频算法,显著的优点是能自适应分析车辆回波,既抑制了交叉干扰项,又保证了时频分辨率[8]。运动车辆回波分解后的微动特征分量IMFk在区间[t-T,t+T]内的AOK-TFR可表示为
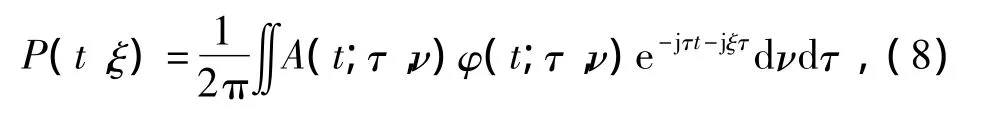
式中:ξ为频率;τ和ν分别为时延和频延;A(t;τ,ν)为短时模糊函数;φ(t;τ,ν)为自适应核函数。与一般核函数相比,自适应核函数能随车辆微动回波变化通过最优核计算准则改变[9],极大地提高了分析微动回波时的自适应能力。
3 运动车辆微动回波分析
通过对运动车辆车体振动和车轮转动复合回波信号S(t)=SZ(t)+Sl(t)的仿真分析,对比EMD和EEMD对车辆微多普勒回波分析效果,并对微动特征模态分量求AOK分布,提取运动车辆微动特征。
3.1 运动车辆回波的EEMD分解
首先利用车辆微动回波模型,对雷达回波进行仿真,仿真参数:雷达载频f0=10 GHz,初始距离R0=2 km,目标平动速度 v=25+2t,雷达视角(α,β)=(π/4 rad,π/36 rad),振动参数(α0,β0,ω,Dv)=(π/6 rad,π/4 rad,10π rad/s,0.2 m),车轮参数(γ,l,d)=(π/6 rad,0.5 m,2 m),采样频率为1 kHz,仿真时长4 s,结果采用归一化表示。在复合回波信号S(t)中加入SNR=5 dB的噪声,EEMD分解时加入方差为0.2的100组高斯白噪声,采用EMD和EEMD分别分解回波。
分别采用EMD和EEMD对车辆复合微动回波进行分解,结果如图4、5所示。就时域分量而言,很难判断2种分析方法的差异,本文提出利用模态分量瞬时频率平稳度的方法比较分解效果。理论上,瞬时频率方差越大,平稳性越差,模态混叠越严重。图6中取EMD分量imf4和EEMD分量IMF4,在信噪比SNR=5 dB和SNR=1 dB时,分别比较车辆微动特征分量的瞬时频率。由图6可见:imf4瞬时频率波动较大,“突变”更明显,即EEMD抗混叠、抗杂波效果更好。为验证这一结论,对前6阶分量瞬时频率方差进行比较,结果如表1所示。
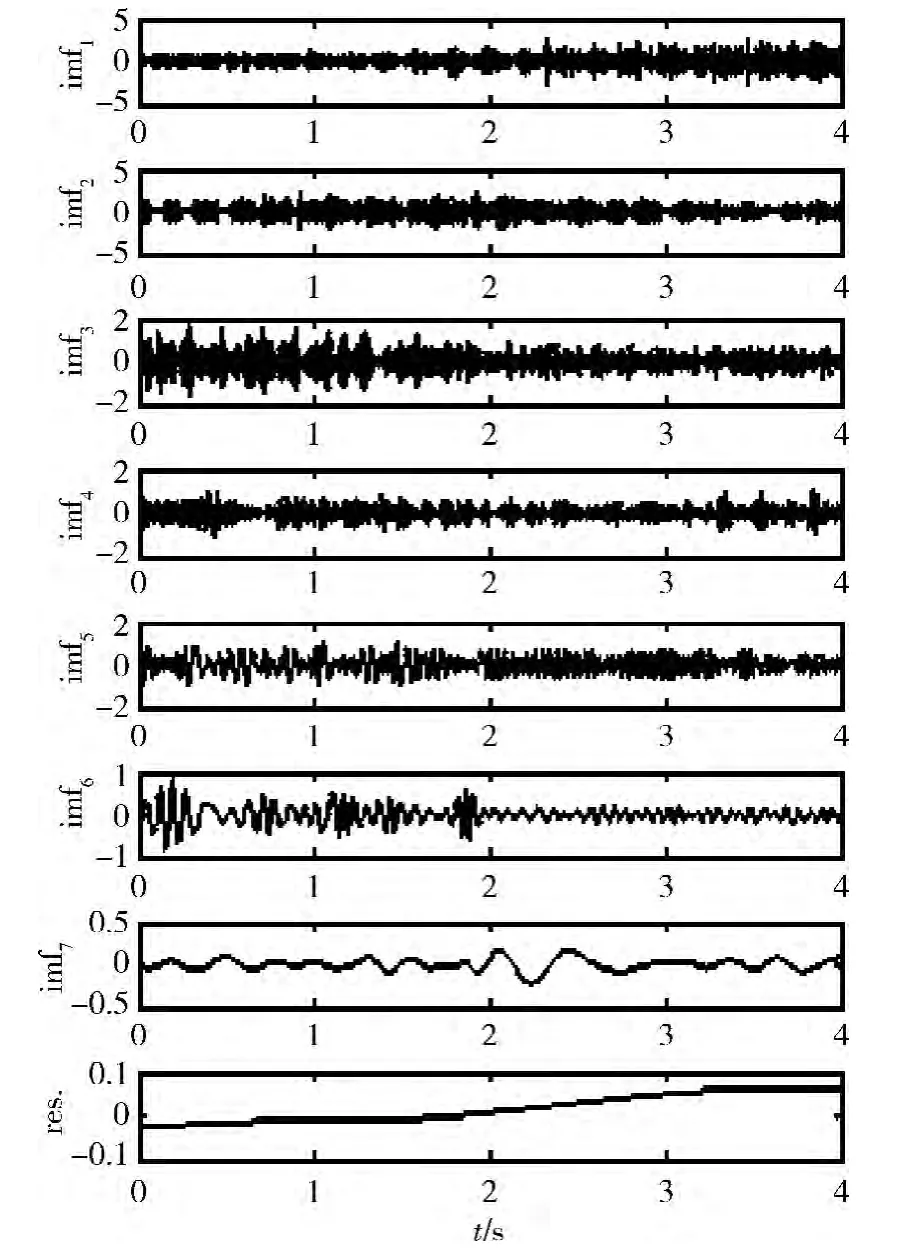
图4 EMD分解车辆回波
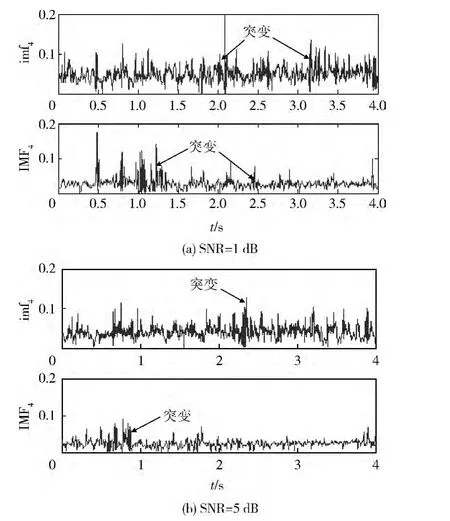
图6 不同信噪比下imf4和IMF4瞬时频率
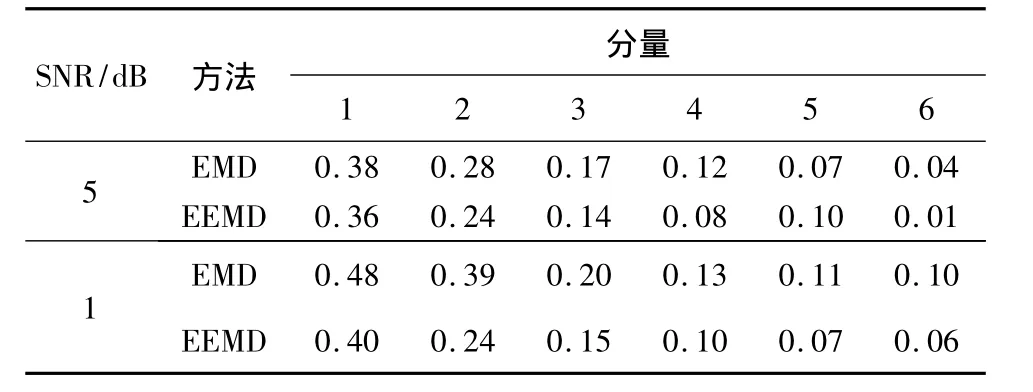
表1 前6阶分量瞬时频率方差
由表1可见:车辆复合微动回波的EMD分量瞬时频率方差总体上大于EEMD分量,从而验证了EEMD分量能更好地抑制模态混叠和噪声干扰。
3.2 运动车辆微多普勒特征提取
由上文分析可知:EEMD在分解运动车辆微动回波时比EMD分解效果更好。传统希尔伯特变换方法是对EEMD分解后分量求Hilbert谱,得到回波瞬时频率分布,如图7所示。
图7对EEMD模态分量直接求Hilbert谱,噪声存在整个时频面内,导致微多普勒特征模糊,不易提取。通过对图5和表1观察,IMF1-IMF3的频率和特征能量都明显高于其他分量,假定为相同微动产生的微多普勒频率,前3阶分量和的AOK时频分布如图8所示,IMF4-IMF7分量和的AOK时频分布如图9所示。
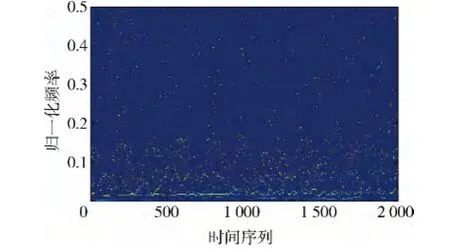
图7 EEMD分解的Hilbert谱
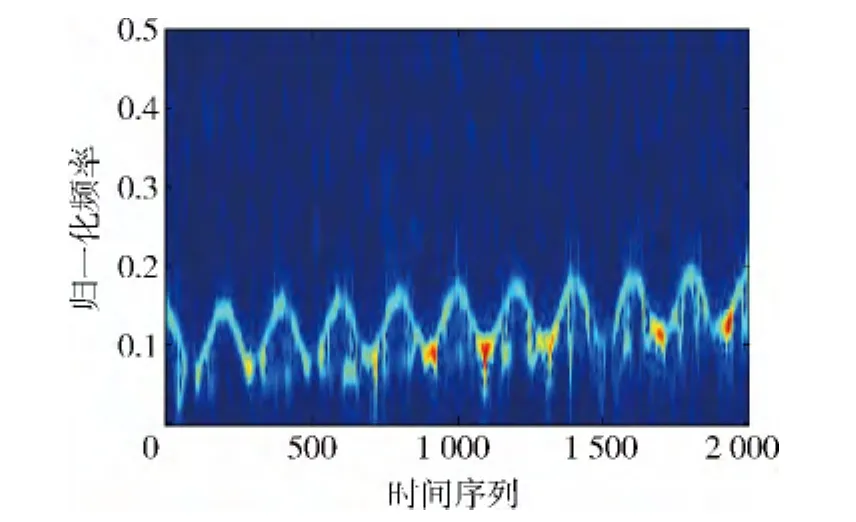
图8 IMF1-IMF3分量和的时频像
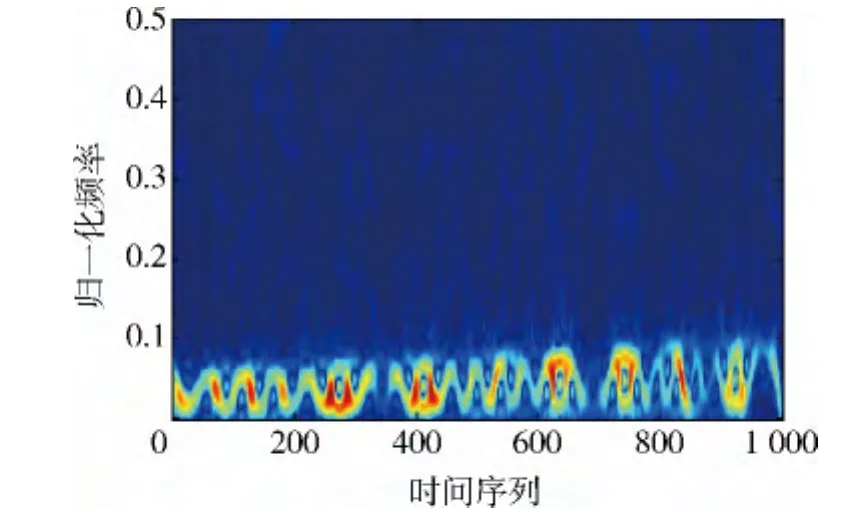
图9 IMF4-IMF7分量和的时频像
由图8可见:时频像微多普勒特征明显,有效抑制了噪声和低频干扰,调制频率约为5 Hz,且频率趋势递增,这和振动角频率为10πrad/s的仿真参数和匀加速平动相吻合,可认为是由振动引起的。由图9可见:频率较小,每个调制周期都有零点,考虑到车轮散射点P运动触地时到雷达径向速度为0 m/s,且模型为6轮,可看作是车轮转动引起的,微多普勒频率波动周期约为8 Hz,即每秒车轮转动8个周期,故平动速度 v=2πlf=2π ×0.5×8≈24 m/s,和速度仿真参数基本吻合。综上所述,利用EEMD联合AOK-TFR方法比较准确地分离并估计了运动车辆不同微多普勒特征参数。
4 结论
通过对车辆运动时微动回波进行分析,提出了利用EEMD联合AOK-TFR提取微多普勒特征的方法。仿真结果表明:该方法较好地分离了低信噪比下车体振动和车轮转动产生的微多普勒频率,能够较准确地提取车体振动频率和车轮转动频率,并估计了车体平动速度,具有抗模态混叠能力强、可有效抑制回波噪声和微多普勒时频分辨率高的优点,为进一步利用车辆运动的微多普勒特征识别坦克、卡车、步战车等地面目标提供了技术支撑。
[1] Chen V C,Li F Y,Ho S S,et al.Micro-Doppler Effect in Radar:Phenomenon,Model and Simulation Study[J].IEEE Transon Aerosp ElectronSyst,2006,42(1):2-21.
[2] Smith G E,Woodbridge K.Template Based Micro-Doppler Signature Classification[J].Radar Conference Manchester,2006,9(3):158-161.
[3] Stove A G,Sykes SR.A Doppler-based Automatic Target Classifier for a Battlefield Surveillance Radar[C]∥Thales Sensors Ltd.Proceedings of IEEE International Conference on Radar.Manchester:IEEE,2002:419-423.
[4] Bai X R,Xing M,Zhou F,et al.Imaging of Micro-motion Targets with Rotating Parts Based on Empirical-mode Decomposition[J].IEEE Transactions on Geoscience and Remote Sensing,2008,46(11):3514-3523.
[5] Cai C J,Liu W X,Fu JS,et al.Radar Micro-Doppler Signature Analysis with HHT[J].IEEE Trans Aerosp Electron,2010,46(2):929-938.
[6] Wu Z H,Huang N E.Ensemble Empirical Mode Decomposition:A Noise Assisted Data Analysis Method[J].Advances in Adaptive Data Analysis,2009,1(1):1-41.
[7] 胡广书.现代信号处理教程[M].北京:清华大学出版社,2004:103-105.
[8] Sun B,Wang E P,Ding Y.Time-frequency Signal Processing for Gas-liquid Two Phase Flow Through a Horizontal Venturi Based on Adaptive Optimal-kernel Theory[J].Chinese Journal of Chemical Engineering,2011(2):243-251.
[9] 张宇辉,金国彬,李天云.基于自适应最优核时频分析理论的间谐波分析新方法[J].中国电机工程学报,2006,26(8):84-89.

