基于小波神经网络的短时交通流预测

金玉婷，余立建

（西南交通大学 交通信息工程及控制实验室，四川 成都610031）

小波分析克服了傅里叶分析的不足，具有良好的时域——频域局部特性和多尺度分辨能力。为提高神经网络的鲁棒性，本文将小波分析与神经网络各自的优点结合，用小波基函数代替传统的Sigmoid函数，形成小波神经网络（Wavelet Neural Network，WNN），并用此来代替BP神经网络对短时交通流量进行预测。

1 基础理论介绍

1.1 小波变换理论

小波变换即为用一个合适的母小波函数ψ（t）通过时间轴上的位移、放缩和幅度的变化产生一系列的派生小波，用系列小波对要分析的信号进行时间轴上的平移比较，获得用以表征信号与小波相似程度的小波系数。

若对∀ψ（t）∈L2（R），如果ψ（t）的傅里叶变换＾ψ（t）满足容许的条件

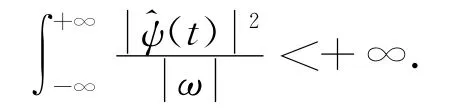
则称ψ（t）为一个基本小波或小波母函数。

小波函数是由一个母小波经过平移与尺寸伸缩得到的，小波变换就是指把某一母小波函数ψ（t）进行平移（平移度为）后，在尺度因子a下与待分析信号x（t）做内积，公式为

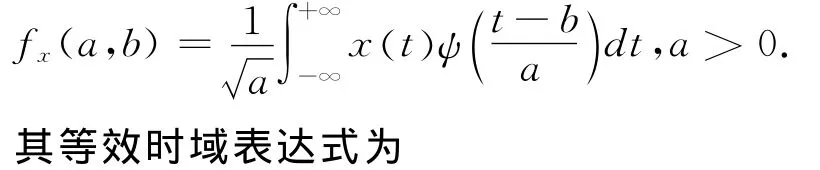
1.2 小波神经网络

小 波 神 经 网 络 （Wavelet Neural Network，WNN）是小波分析与神经网络理论相结合的产物，可概括为两类:松散结合类以及紧密结合类。

松散结合类又称小波与神经网络的无机式结合，它是一种以小波分析为基础的信号预处理，处理后的信息再传输给神经网络进行处理的一种方式。

紧密结合类又称小波与神经网络的有机式结合，是目前研究小波神经网络广泛采用的一种结构形式。它的基本思想由Zhang Qinghua等人于1992年正式提出，即用小波函数来代替常规神经网络的隐含层函数，同时相应的输入层到隐含层的权值及隐含层阈值分别由小波基函数的尺度参数和平移参数来代替。文中采用紧密结合类的小波神经网络。

2 仿真预测模型及算法

2.1 仿真预测模型

由于三层结构模型（输入层，隐含层，输出层）是解决单一非线性问题的最简单且最有效率的结构，且少于三层无法逼近非线性曲线，而多于三层又会大大增加复杂度和训练时间。因此，本文中小波神经网络预测模型采用三层网络拓扑结构，结构模型如图1所示。

图1 小波神经网络预测模型

根据需要，设定在输入层中有n个输入，即一次输入含有n个元素的输入序列，n表示预测序列值与它之前的相关度，或者称相关步数。隐含层包含m个神经元。输出层有1个神经元，输出为第t＋1个时间序列的预测值。其中w2ij表示从输入层的第i个神经元到隐含层的第j个神经元之间的权值，w3jk表示第j个隐含层神经元到输出层神经元之间权值。隐含层节点的传递函数φ为小波基函数。

在输入信号序列为xi（i＝1，2，…，k）时，隐含层输出计算公式为

式中:h（j）为隐含层第j个节点输出值，wij为输入层和隐含层的连接权值，bj为小波基函数的平移因子，aj为小波基函数的伸缩因子，hj为小波基函数。

小波基函数的选取有多种选择，目前常用的母小波有Haar小波、Shannon小波、墨西哥帽小波和Morlet小波等，根据实际需要，本文采用国际常用的小波基函数Morlet母小波基函数，数学公式为

函数图形如图2所示。

图2 Morlet母小波基函数图形

可以看出，小波神经网络输出层的计算公式为

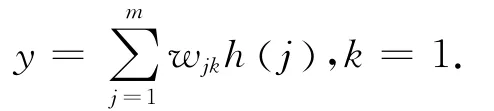
式中:wjk为隐含层到输出层权值，h（）j为第j个隐含层节点的输出，m为隐含层节点数。

2.2 仿真预测算法

小波神经网络权值参数修正算法类似于BP神经网络权值修正算法，采用梯度修正法修正网络的权值和小波基函数参数，从而使小波神经网络预测输出不断逼近期望输出。

小波神经网络训练算法步骤如下:

1）初始化。随机初始化伸缩因子、平移因子以及连接权重，并根据需要设置网络学习速率。

2）样本分类。把事先准备好的样本数据分为训练样本和测试样本，训练样本用于训练网络，测试样本用于测试网络预测精度。

3）预测输出。把训练样本输入网络，计算网络预测输出并计算网络输出和期望输出的误差e。

4）权值修正。根据误差e修正网络权值和小波函数参数，使网络预测值逼近期望值。

5）判断算法是否结束，如若没有，返回步骤3。

小波神经网络训练完成后，用测试样本对网络进行预测仿真，根据仿真的效果来评价网络的性能。综上所述，基于小波神经网络的短时交通流量预测流程如图3所示。

图3 小波神经网络预测流程

3 预测网络仿真及评价

3.1 数据的来源、处理以及网络的评价指标

实验采用交通流数据，运用美国加州高速公路通行能力度量系统数据（Caltrans Performance Measurement System ，简称PeMS）中数据库第7区某检测器2013－08－06～2013－08－09的交通数据，数据采样间隔为5min，数据总数量达到1 152。将搜集的数据进行归一化预处理，并将前3d的交通流量数据作为训练样本，第4d作为测试样本，即通过前3d的训练之后，对第4d的交通流量情况进行预测。

短时交通流预测问题——时间序列预测问题，即用神经网络来拟合一个函数，然后用这个函数求得某一点的未来值。如何根据不同对象的时间序列找到神经网络的输入量维数m是建立预测模型的关键一步，这就是相空间重构问题。

由于小波神经网络模型输入为3维数据，所以要把一维的时间序列转换成3维的数据矩阵，本文采用时间延滞技术，把一维的时间序列嵌入到m维空间中去，从时间序列中得到动力系统相空间的几何结构，只要得到延滞参数τ和嵌入维数m就可以确定预测模型的输入向量，即小波神经网络的输入层神经元个数。利用原始数据经过计算可以得到其延滞参数τ和嵌入维数m分别为24和3。

为了评价交通流量预测的效果，我们常用到的几个评价指标有平均相对误差（Mean Relatively Error，MRE）、均方误 差 （Mean Square Error ，MSE）和均等系数（Equalization Coefficient，EC，即拟合度）。本文引入以上几种评价指标:

1）平均相对误差

2）均方误差

3）拟合度

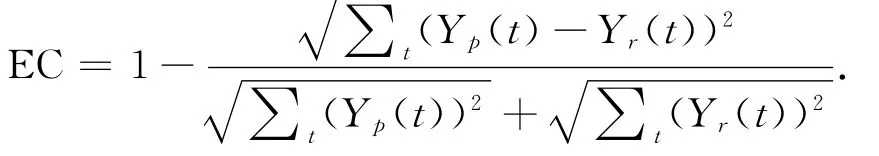
式中:Yp（t）为预测的输出，Yr（t）为实际的输出。

MRE可以用来表征预测值与真实值偏离的程度。它的值越小说明预测值与实际值偏离越小，预测效果越好。MSE是用来反应误差分布情况的，它的值越小误差分布就比较集中，预测效果就越好。EC值的大小用来表明预测值与真实值之间的拟合程度，它的值越大，说明曲线拟合程度越高，预测效果也越好。一般情况下，较好的预测其EC值应大于0.85，若大于0.9则认为是可用性较高的预测。

3.2 预测网络仿真

由于隐含层神经元个数的确定直接关系到预测精度的高低，本文采用“拼凑法”来确定隐含层神经元个数。虽然这种方法费时，但它是目前确定隐含层神经元数最有效和简单的常用方法，以本文某次实验为例。测试网络为传统BP网络，训练次数为100，不同隐含层神经元个数所产生的效果也不同，经过测试，当隐含层神经元个数为8时，预测网络的各项指数最好，这时的网络输出与期望的输出最为接近，所对应的预测效果也就最好。

确定了隐含层神经元个数之后，就可以用已经确定好的网络拓扑结构去构造仿真环境。先用传统BP神经网络测试，BP神经网络模型采用3－8－1结构，即输入3个神经元，隐含层8个神经元，输出1个神经元。输入层3个神经元代表模型设定的相关度T＝3，学习速率lr＝0.01。训练目标goal＝0.007 5，先设定最大训练次数为100次。仿真软件采用Matlab2010b，仿真结果如图4、图5所示。

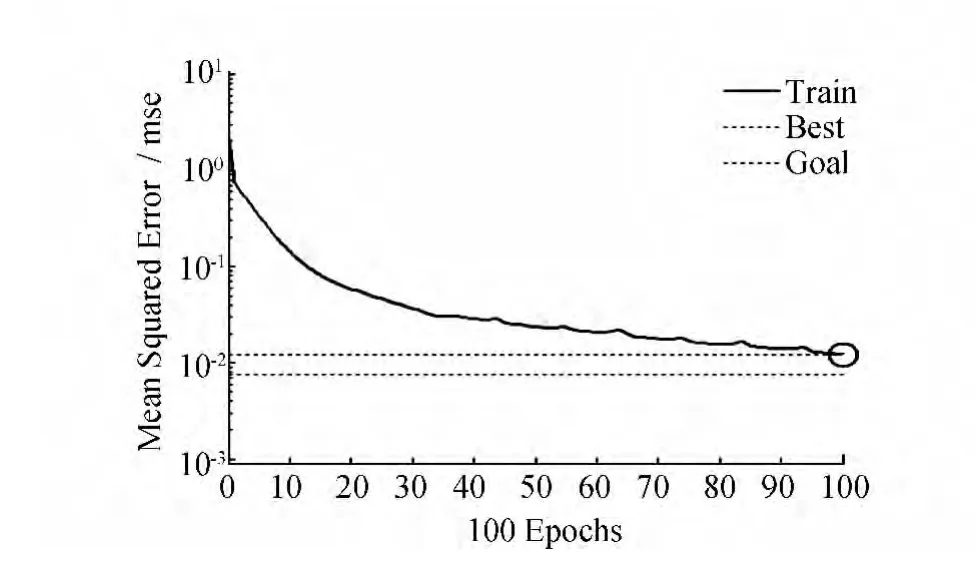
图4 训练100次时BP神经网络训练过程

图5 训练100次时BP网络的预测效果和误差直方图

此时，BP网络预测交通流量的性能指标为:MSE＝464.253 667 36，MAPE＝ 20.07%，EC＝0.863 900 22。

使用小波神经网络在低训练次数环境中测试，网络模型同样采用3－8－1结构，权值更新学习速率lr1＝0.01。小波基函数伸缩因子和平移因子的更新学习速率为lr2＝0.001，最大训练次数为100次。仿真结果如图6、图7所示。

图6 训练100次时小波神经网络训练过程

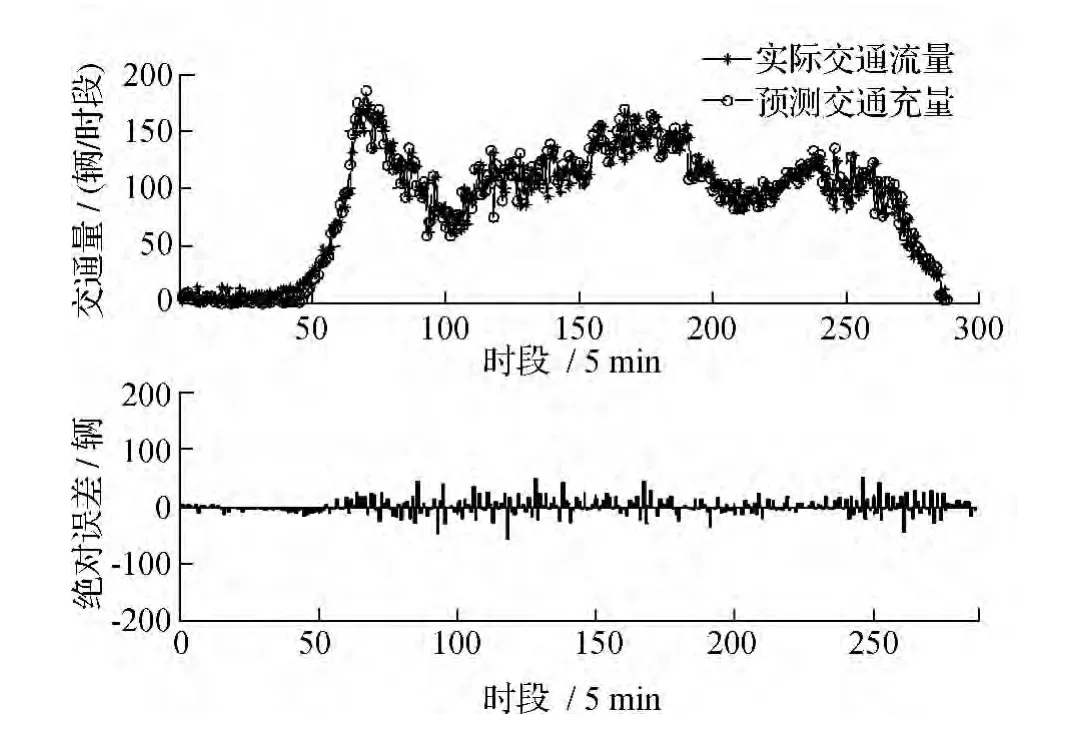
图7 训练100次时小波神经网络的预测效果和误差直方图

此时，小波网络预测交通流量的性能指标为:MSE＝257.249 918 13，MAPE＝ 12.57%，EC＝0.924 819 86。

3.3 预测网络仿真

可以看出，传统BP网络在低训练次数（100次）的情况下对交通流量的预测效果不理想。在网络训练中收敛较慢，训练100次还未达到预设的收敛值，并且预测相似度值（EC值）只有86.39%，达不到须大于90%预测精度要求，在上午10时左右存在着极大的预测误差。而小波神经网络在低训练次数的情况下对交通流量的预测效果相比较于传统的BP网络有着压倒性的优势，网络训练过程中收敛极快，在训练次数为10次的情况下就基本达到了所预期的效果，预测相似度更是高达92.48%。然而，对于小波神经网络而言，低训练次数所带来的问题就是不稳定，训练次数达到62次左右的时候网络发生了一次震荡。这对于实际应用中的预测是不利的。

为了克服上述问题，解决方法就是增加训练次数来增加网络的冗余性和容错率，训练次数为500次时，再次实验BP网络和小波神经网络的网络预测性能。为了便于比较，两组对于短时交通流量的预测实验，及二者的性能指标对比如表1、表2所示。

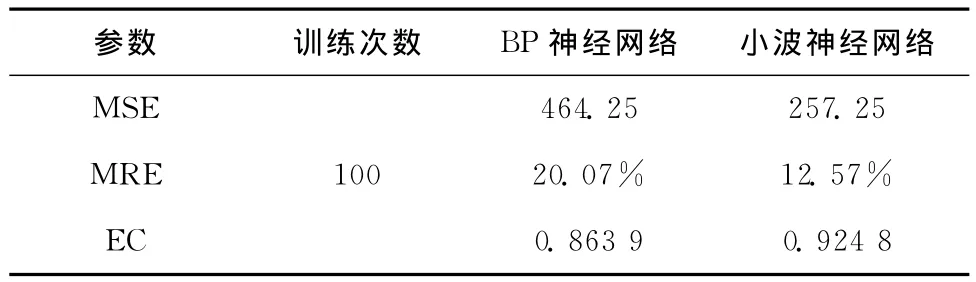
表1 低训练次数下BP网络与小波神经网络对于短时交通流量的预测的性能指标

表2 高训练次数下BP网络与小波神经网络对于短时交通流量的预测的性能指标

4 结束语

本文提出了将小波分析与神经网络相结合的方法来对短时交通流进行预测，并把预测结果与传统BP神经网络预测结果相比较，发现预测精度不仅有了极大的提高，而且收敛的速度也相较于传统BP神经网络有着无可比拟的优势。由此可知，使用小波神经网络预测短时交通流量更为合适。

［1］李波.基于小波分析和遗传神经网络的短时城市交通流量预测研究［D］.北京:北京交通大学，2012.

［2］姚智胜.基于实时数据的道路网短时交通流预测理论与方法研究［D］.北京:北京交通大学，2007.

［3］谢忠玉，韩桂华，初红霞，等，两种短时交通流混沌预测方法分析［J］.交通科技与经济，2011，13（4）:110－112.

［4］陈振伟，郭拯危.小波神经网络预测模型的仿真实现［J］.计算机工程与科学，2005，25（6）:147－150.

［5］魏立龙，许东方，孙浩，等.基于遗传算法的小波神经网络在股票预测中的应用［J］.信息与电脑，2011，5（5）:130－131.

［6］魏文，徐立建，龚炯，等，基于混沌理论和PSO神经网络的短时交通流预测［J］.物流工程与管理，2010，32（2）:75－77.

［7］史峰，王小川.MATLAB神经网络30个案例分析［M］.北京:北京航空航天大学出版社，2010.

［8］张德丰.MATLAB神经网络应用设计［M］.北京:机械工业出版社，2009.

［9］李万庆，张金水，孟文清，等.基于小波神经网络的房地产价格指数预测研究［J］.河北工程大学学报，2008，25（1）:74－76.

［10］郑长江，陈田星.基于小波神经网络的路段短时交通流预测［J］.大连交通大学学报，2012，33（5）:50－53.