独立需求生产批量优化问题的遗传算法实现

卫 妍

（兰州交通大学 交通运输学院，甘肃 兰州730070）

生产批量问题是企业生产管理中一个常见的约束批量问题。主要目标是确定最优的生产批量，使得生产费用、生产准备费用和库存费用综合指标最小。MRPII是在MRP的基础上发展起来的，它主要在考虑市场的需求、企业的生产能力和对用户的服务水平等诸多因素的前提下安排企业的生产发展战略:①长期规划（公司层）；②中、短期生产计划 （分厂或车间层）；③生产计划的具体实现（车间或班组层）。在MRPII中，第②层的主要问题之一是生产计划中的约束批量问题。对该问题的研究，可以指导在生产实践中的批量生产问题，并为企业生产产生重大的经济效益。

1 模型建立

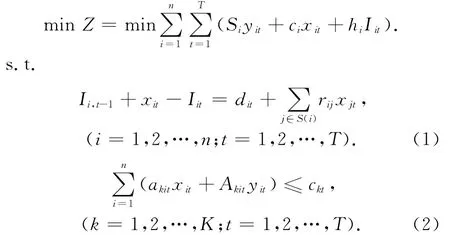
本文建立的是基于独立需求的生产批量优化问题的遗传算法，所以对该批量生产问题做如下假设。

假设:该问题中对各产品的需求是独立的。原模型:

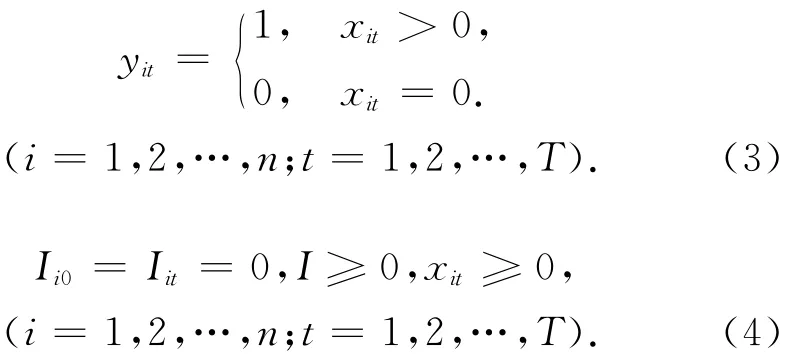
式中:T为计划时段，如一年的12个月，一周5d等；n为产品的品种数；xit为决策变量；Iit为决策变量；dit为时段t内对产品i的需求量；Si为生产产品i时的生产准备费用，这一费用是由于机器要求更换加工产品而一次性发生的；ci为单位产品i的生产费用；hi为单位产品i的库存费用；akit为时段单位产品i占用资源k的量；Akit为t时段产品i的生产准备占用资源k的量；ckt为t时段资源k的可提供量；rij为产品j的生产过程中对产品i的需求量，由于本文是基于独立需求的生产批量问题，所以rij＝0。式（1）的约束条件变为

2 问题求解

主要思想:

1）每次记录下当前较优解，单点交叉法、交配概率Pc＝0.6。

2）交配后代直接替代双亲，而将没有交配的双亲使其直接遗传到下一代，从而使得交配后的群体规模同旧群体的规模相同。

3）再以p＝0.14的概率变异。更新当前最优染色体的进化循环过程。

2.1 编 码

本文xit，Iit为连续性决策变量，所以通过产生特定范围的随机数初始化为各阶段生产品量，并且将其转换为二进制编码当作染色体，yit根据生产批量确定是否为1或0。当xit＞0时，yit＝1；否则，yit＝0。初始种群

由于生成的初始解有可能不是可行解，可根据约束式（1）、式（2）、式（4）来剔除。

2.2 交配规则

本文使用单点交叉法:确定双亲后，随机选择一个交配位，然后交换交配位后面的基因，对换后形成两个后代。

2.3 变 异

使用随机函数Random（）先从种群中选出个体，再随机选出一个生产阶段中的某个产品，对其随机位进行变异。

2.4 种群选择

计算过程中，通过计算获得较小目标函数值并将该个体的信息记录下来，计算出概率，将大于设定概率的个体二进制编码两两交叉变异，获得新的种群。此时计算出新种群的目标函数值，与记录中的目标函数值作比较，将新旧种群中的优秀个体再重新组成下一代新种群。依次重复，得到收敛目标函数值。

3 算法及流程

在算法编写过程中做到较优种群的及时记录和更新。本文在初始化种群时，为减少不可行解的产生，在产生同一阶段的生产批量时，使用下式:

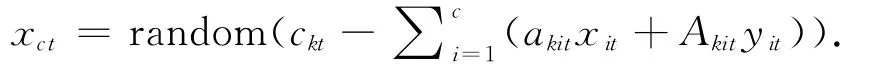
xct为t阶段生产c的批量，其他同上。因此，产生的个体具有较强的可行性。

在交配函数中，采用双亲双子交配规则进行交叉后，对Iit和yit进行计算和更新。然后进行选择变异，接下来剔除不可行的个体。为了保证种群的规模不变，在计算时，首先会将上次的记录中未参与交配的个体加入计算种群中。

最后，经过100次迭代，得到100次中最优值和最差值、平均值，以及最优与最差的差值，分别与最优和最差的比。算法流程图如图1所示。

图1 算法流程

4 计算结果与结论

本文采用VS2010对独立需求生产批量优化问题的遗传算法进行编程实现，在n＝7，Pc＝0.6，Pm＝0.14时，分别对阶段T＝5，15，20，…，35进行100次模拟计算，所得结果如表1所示。

为了加快该遗传算法的收敛速度，本文在传统二进制遗传算法中引入了记忆机制。应用改进的算法求解了一个具体实例，结果表明该算法不论在寻优能力方面，还是在求解速度和稳定性方面都取得很好的效果，能够较好地解决基于独立需求的约束生产批量计划问题。

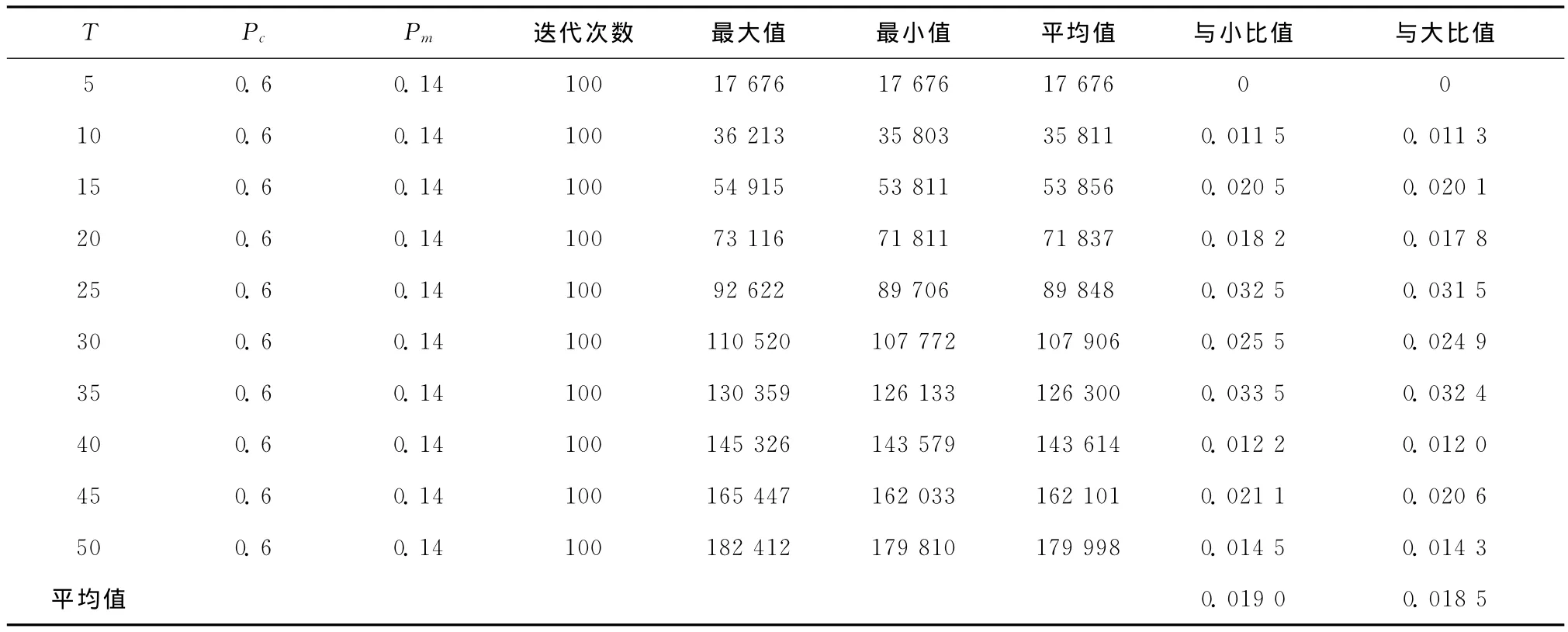
表1 算法结果

［1］邢文训，谢金星.现代优化计算方法［M］.北京:清华大学出版社，1999.

［2］潘正君，康立山.演化计算［M］.北京:清华大学出版社，1998.

［3］谢金星，姜启源，邢文训.能力受限的批量问题的数学模型与算法新进展［J］.运筹学杂志，1996，15（1），1－12.

［4］唐立新，杨自厚，王梦光.单级无能力约束批量问题大小问题的遗传搜索算法［J］.东北大学学报，1997（3）:46－48.

［5］王锡凡.电力系统优化规划［M］.北京:水利电力出版社，1990.

［6］李茂军，童调生.单亲遗传算法及其全局收敛性分析［J］.自动化学报，1999，25（1）:68－71.

［7］李睿，孙有信，吴德瑄，等.基于遗传算法的供应链分层协调机制［J］.交通科技与经济，2012，14（1）:93－95.