灰色预测模型在铁路客流预测中的应用

黄召杰，冯 硕

（1.北京铁路局南仓站，天津300000；2.北京铁路局石家庄培训基地，河北 石家庄050000）

1 模型介绍

1.1 灰色预测概念

灰色系统预测理论的基本思路是按某种规则将已知的数据序列构成非动态的或动态的白色模块，然后按照某种变换解决来求解未来的灰色模型。在灰色系统理论中，常用的模型是微分方程所描述的动态方程，最简单的是基于灰色系统理论模型GM（1，1）以及GM（1，N）模型的预测分析。灰色预测分析可分为几类，即数列预测，灾变预测，季节性灾变预测，拓扑预测及系统综合预测。

1.2 灰色预测模型

灰色理论的微分方程模型称为GM模型，GM（1，N）表示一阶、N个变量的微分方程模型，GM（1，1）表示一阶、单个变量的微分方程。

1.2.1 GM（1，1）模型

GM（1，1）是一阶单序列的线性动态模型，用于时间t序列预测的是其离散形式的微分方程模型，具体形式为

由上式可知，这是一个单变量x对时间的一阶微分方程，是连续的，实际使用的是其离散的单个数据形式。

设 有 数 列x（0）共 有n个 观 察 值x（0）（1），x（0）（2），x（0）（3），…，x（0）（n），对x（0）作一次累 加 生成，得到新的数列x（1），表达式为

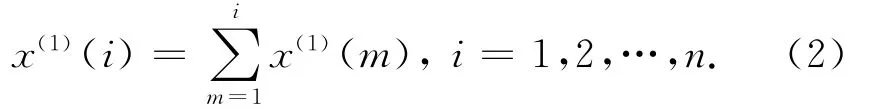
対一阶生成数列x（1）建立预测模型，其方程为

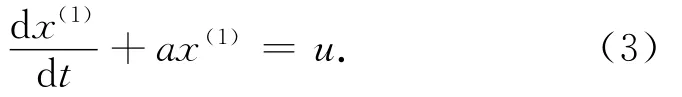
式中:a，u为待估参数，分别称为发展灰数和内生控制灰数。

将上式的离散形式展开，可得

将两个待估模型参数表示为向量形式得

将上述离散方程组用最小二乘法求解，得

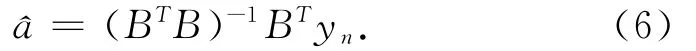
将上式中的＾a代入上式，解微分方程，得到GM（1，1）的预测模型为

式中

1.2.2 GM（1，N）模型

对于n个变量x1，x2，…，xn，如果每个变量都有m个相互对应的数据，则形成n个数列展开为

对x（1）i累加生成，形成n个生成数列x（1）i有

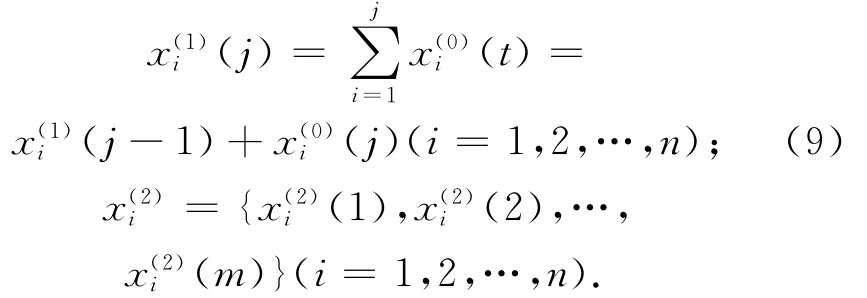
则

可建立微分方程

上式中的参数可表示为

按最小二乘法估计参数＾a，则有

可得GM（1，N）模型为

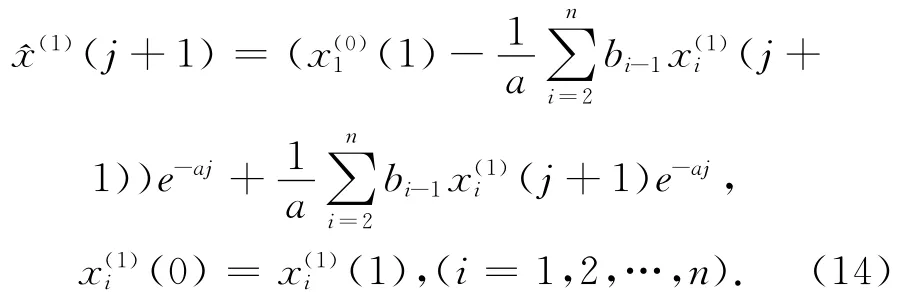
1.2.3 模型检验

灰色预测模型的检验，有关联检验、后验检验和残差检验。残差检验分两种:一是相对误差，二是绝对误差。检验步骤为

设 原 始 序 列:X0＝ （x（0）（1），x（0）（2），…，x（0）（n）），灰色模型预测序列为

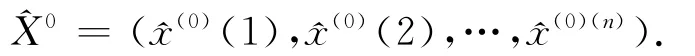
计算残差

计算相对误差

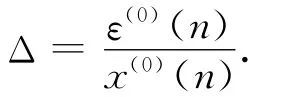
计算x（0）（n）的均值和方差为

计算ε（0）（n）的均值和方差为

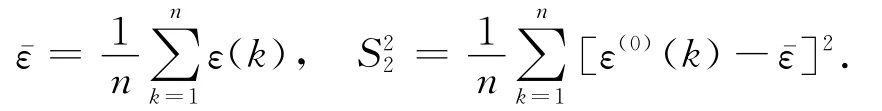
称为均方差比值 ，称p＝为小误差概率。

C＝S2

S1

一般精度等级的划分如表1所示。

表1 灰色预测精度等级

如果关联度、方差、小误差概率和相关误差比都在允许范围之内时，则可用所建模型进行预测，否则应进行残差修正。

2 具体实例

用2007～2010年的数据来预测2011年的1～9月各月客运量，建立铁路客运量灰色系统预测模型。

以2011年1月客运量预测为例，2007～2010年各年1月客运量如表2所示。

表2 2007～2010年各年1月客运量

由表1中2007～2010年各年1月的客运量可知

求得一次累加生成数列

即

预测模型为

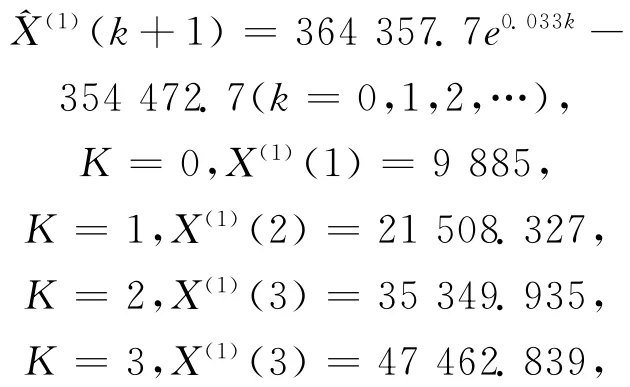
累减生成

计算绝对误差序列

相对误差序列

关联度检验

不满足ρ＝0.5时，γ大于0.6的要求，所以，要对模型进行残差修正，取

修正后的模型为

由修正后的模型计算得到2011年1月的预测值为15 226.102万人。用同样的方法计算2011年其他各月的预测值（见表3）和灰色预测值与实际值的拟合值（见图1）。

表3和图1可以看出，虽然有些月份预测值与实际值拟合效果一般，但总体预测值与实际值拟合效果较好。

表3 2011年客运量实际值与灰色预测值分析表

图1 灰色预测值与实际值拟合结果

3 结 论

1）灰色预测方法简单。虽然该模型是建立在高等数学基础上，但计算步骤简单，可以借助计算机软件或者Excel很容易计算出来，计算时间短。

2）灰色预测模型需要的数据少。由于灰色预测把随机过程看作灰色过程，所以，灰色预测只根据实际情况选择适量的数据即可。

3）灰色预测可有效的处理贫信息和数据少的情况。在一定时间段内预测的精度较高，但是随着信息的增加，不断进入灰色系统时，会发现预测效果越来越差，灰色系统不适合长期的预测，不能用该模型预测未来的所有值。

［1］张永波.基于灰色系统理论的预测模型的研究［M］.哈尔滨:哈尔滨工程大学出版社，2005.

［2］闵惜琳.基于灰色预测模型的人才需求分析［J］.科技管理研究，2005（6）:72－77.

［3］何静.京津客运专线短期客流预测研究［M］.北京:北京交通大学出版社，2006.

［4］韦英娜，吕从高.基于灰色模型的铁路货运量预测［J］.货物运输，2007（7）:16－17.

［5］邓聚龙.灰色系统（社会，经济）［M］.北京:国防工业出版社，1985.

［6］吕从高.城际客运专线客运量预测理论及方法研究［D］.成都:西南交通大学，2008.

［7］任民.铁路客运专线运量预测方法研究［J］.铁道工程学报，2008（5）:89－92.

［8］唐小我.预测理论及其应用［M］.成都:电子科技大学出版社，1992.

［9］赵海青.灰色马尔科夫预测模型及其在市盈率预测中的应用［J］.保定师范专科学校学报，2006，19（2）:15－17.

［10］马琰.组合预测模型在航空客运量预测中的应用［D］.长沙:中南大学，2008.

［11］黄召杰，陈伟.组合预测方法在我国铁路客流预测中的应用［J］.交通科技与经济，2011，13（4）:97－98.