相位平滑伪距差分技术在北斗定位中的应用探讨

凌 青，于清波

（1.江苏省交通规划设计院股份有限公司，江苏 南京210014；2.天津市普讯电力信息技术有限公司，天津300384）

载波相位平滑伪距差分技术可以消除或削弱很多卫星定位的误差源，从而提高定位的精度，已被广泛应用于GPS导航定位中。唐卫明、范士杰、张成军等分析了GPS载波相位平滑伪距的精度，得出载波相位平滑伪距精度可达到分米级的结论；常志巧、周泽波、谢翔等人继续研究了GPS载波相位平滑伪距差分技术在定位导航中的应用，表明利用载波相位平滑伪距差分技术可实现优于0.4m的定位精度。北斗卫星导航系统采用与GPS系统相同的被动式定位原理，但同时又具有自己独特的星座系统和信号频率等特点。因此，这里将载波相位平滑伪距差分技术应用到北斗系统中，来实现北斗的高精度定位服务。

1 模型推导

1.1 伪距双差定位模型

假设有两台静止的北斗接收机1和2，对卫星i进行了同步观测，将1视为基准站，2视为流动站，则北斗伪距的非差观测方程分别为

1）对基准站1，有

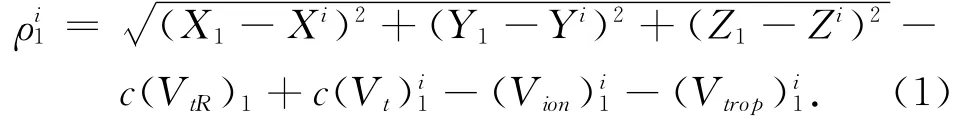
2）对流动站2，有

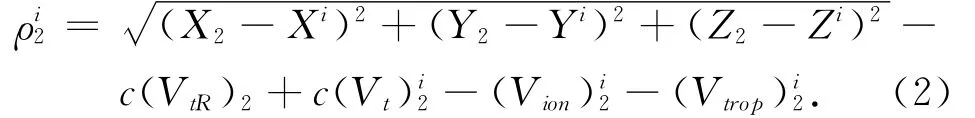
对伪距观测方程在测站和卫星间求二次差，得到伪距的双差观测方程为，其中

若以Nr和Ns表示包括参考站在内的测站总数和同步观测的卫星数目，则有方程总数，未知数总数为3（Nr－1）。由此可得，在任一历元环境下观测数据的求解条件为或

从伪距双差观测方程可以看出，伪距观测方程消除了接收机钟差和卫星钟差的影响，削弱了对流层和电离层等误差的影响，特别是在短基线中尤为明显。

1.2 载波相位平滑伪距

在这里我们只列出伪距与载波不同的误差项，相同误差项省略，则伪距和载波的观测方程为

式中:ρ为卫星到接收机的几何距离；Vion为电离层延迟项；ΔDΦ，ΔDp分别为伪距和载波的多路径效应影响；εΦ，εp分别为伪距和载波观测噪声；N为整周模糊度。

由于相位的多路径效应影响和观测噪声相比伪距很小，忽略ΔDΦ，εΦ两项，由式（4）和式（5）得

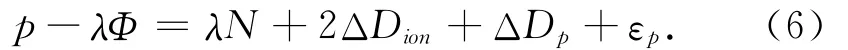
顾及到一定历元内，伪距的多路径效应和观测噪声的随机性，认为两者的均值为0，而电离层折射变化很小，可视为常数，有

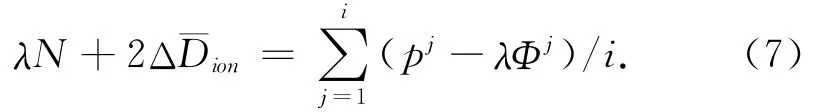
式中:i为历元序号，j＝1，2，3，…，i。

从而可以得到第i个历元上的平滑伪距为

在实际计算中，常采用Hatach滤波公式

当i＝1时，ω＝1以后按历元递减，减少伪距权重，并充分利用载波的高精度观测值。文中采取将加权值ω按0.01逐历元递减，第100个历元后便不再变化，结果证明该定权方法效果较好。实际操作中周跳和平滑窗口的合理选择对平滑结果影响很大，如果存在周跳，上述算法将会失效。一个简单的探测数据不规则变化（如周跳）的方法是，检查两个相邻历元相位差与多普勒频移值乘以两个历元时间间隔的一致性。周跳出现后，须将加权值ω重置1，这将完全消除载波观测值中的错误信息影响。

2 实验实例

为验证北斗单双频相位平滑伪距差分定位技术的可行性和有效性，采用两台司南M300GNSS接收机进行静态实验，数据采样率为1Hz。两台接收机分别位于上海市徐汇区莲花路的两栋大楼楼顶，选取观测条件较好的2012－12－26上午10:00～10:30的观测时段（周跳粗差已经剔除），解算一条长度为126.713m的基线，基线长度通过全站仪准确测量得到。

为了比较研究载波相位平滑伪距差分技术改善伪距差分定位的效果，采用四种方案进行解算:单频伪距差分解算；双频伪距差分解算；单频载波平滑伪距差分解算；双频载波平滑伪距差分解算。将0.5h的载波相位差分定位结果当作“准确值”，四种解算方案的结果分别与“准确值”作差对比，截取了600个历元的残差图。其中蓝线、绿线、红线分别代表X、Y、Z轴方向的残差，结果如图1～图4所示。

将图3，图4的实验结果与图1，图2的结果对比我们可以看到，北斗单双频载波相位平滑伪距差分，较直接伪距差分定位的精度和稳定性都有了明显提高；直接伪距差分得到的各历元间的结果抖动剧烈，而经过平滑后的值变化就会相当平缓。这是由于载波观测值的观测精度较高且有较小的观测噪声，经过相位平滑后的伪距观测值精度明显提高了；而伪距差分定位结果中的观测残差较大，受到测量噪声的影响使其变化具有随机性。

图1 单频伪距双差位置坐标残差

图2 双频伪距双差位置坐标残差

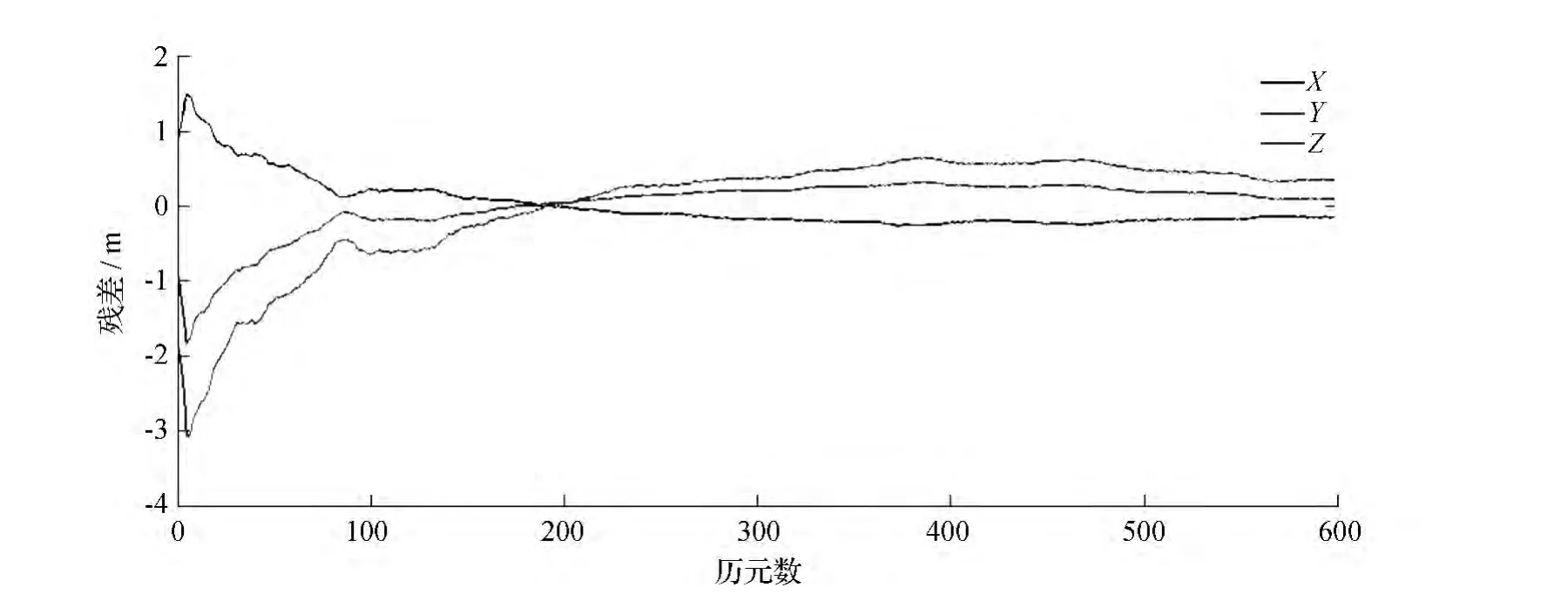
图3 单频相位平滑伪距双差位置坐标残差

对比图1与图2可以看到，单频伪距双差定位的残差曲线与消去电离层的双频伪距双差定位的残差曲线在X，Y，Z三向的走势基本一致，但后者较前者更加平缓，这是由于双频伪距组合消去了电离层延迟噪声的影响。

对比图3与图4可以看到，单频相位平滑伪距差分和双频相位平滑伪距差分的X，Y，Z三向残差曲线的走势基本一致，但单频平滑伪距差分得出的残差曲线比双频平滑伪距差分残差曲线更加光滑。这说明双频平滑伪距虽然可以消除电离层延迟影响，使平滑滤波不易发散，但是观测噪声却比单频增加了。

最后，统计出0.5h观测时段内直接伪距差分、单频载波平滑伪距差分、双频载波平滑伪距差分解得的基线在X，Y，Z三向的中误差，及基线长度S的中误差，结果如表1所示。

图4 双频相位平滑伪距双差位置坐标残差图

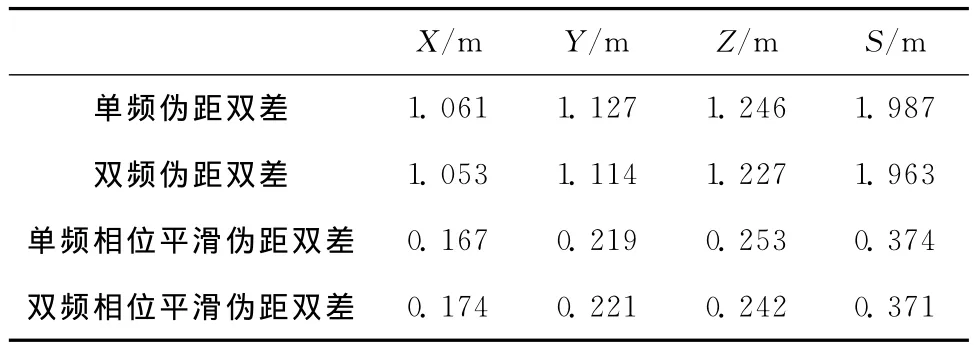
表1 误差对比

从表1的结果我们可以看到，无论单频相位平滑伪距差分技术还是双频相位平滑伪距差分技术，都可以将直接伪距差分定位的精度提高5倍左右，并且双频相位平滑伪距差分相比单频相位平滑伪距差分在定位解算的精度上没有明显提高；同样的，双频伪距双差定位相比较单频伪距双差定位在精度上略有提高，但不十分明显。在本实验的相对定位解算中，北斗相位平滑伪距差分定位的精度可以达到0.4m以内，可以用于高精度的定位。这与文献研究中的GPS相位平滑伪距为30～60cm定位精度的结论一致，说明载波平滑伪距差分技术可以用于北斗卫星导航系统，并且可以达到其在GPS应用中的同等精度。

3 结束语

通过实测的北斗数据实验，对平滑前后的伪距差分定位结果进行了对比分析。结果表明，用北斗载波相位平滑后的伪距作差分定位可以明显地提高定位的精度和稳定性。在短基线的相对定位中，无论是直接伪距定位还是相位平滑伪距定位，双频组合观测值较单频观测值对定位精度的提高并不十分明显。同GPS一样，北斗载波相位平滑伪距差分技术可以有效提高定位导航的精度和稳定性，算法也不复杂。

［1］杨元喜.北斗卫星导航系统的进展、贡献与挑战［J］.测绘学报，2010，39（1）:1－6.

［2］刘基余.北斗卫星导航系统的现况与发展［J］.遥测遥控，2013（3）:1－8.

［3］刘伟平，郝金明，李建文，等.一种北斗卫星精密定轨方法［J］.测绘科学技术学报，2013（3）:247－250.

［4］唐卫明，刘智敏.GPS载波相位平滑伪距精度分析与应用探讨［J］.测绘信息与工程，2005（3）:37－39.

［5］范士杰，郭际明，彭秀英.GPS双频相位平滑伪距及其单点定位的精度研究［J］.测绘工程，2005（4）:39－42.

［6］张成军，杨力，陈军.提高GPS载波相位平滑伪距定位精度的算法研究［J］.大地测量与地球动力学，2009（4）:106－110.

［4］罗和平，邱蕾.利用载波相位平滑伪距分析深圳市电离层变化规律［J］.测绘工程，2014，23（2）:54－56.

［8］常志巧，郝金明，李军正.载波相位平滑伪距及其在差分定位中的应用［J］.海洋测绘，2009（3）:21－23.

［9］周泽波，沈云中，李博峰.基于相位平滑伪距与多普勒数据的GPS动态定位［J］.大地测量与地球动力学，2008（3）:59－63.

［10］伍岳，邱蕾.网络RTK模式下多频载波相位观测值解算整周模糊度［J］.测绘工程，2013，22（4）:1－4

［11］谢翔，喻小东，郭际明，等.单频相位平滑伪距差分技术监测动态目标分析［J］.测绘地理信息，2013（2）:14－16.

［12］张亮，岳东杰.相位减伪距法与电离层残差法探测和修复周跳［J］.测绘工程，2014，23（2）:36－38.

［13］彭秀英，郭际明，薛树强.GPS单频伪距相位平滑及其单点定位的精度分析［J］.测绘科学，2011（5）:39－41.