基于蚁群算法的车辆调度问题

王建玲，齐紫茜，何 璐

（上海海洋大学 工程学院，上海201306）

随着运输的发展，物资的流通从单一的车辆配送运输发展到了大规模的车辆配送系统，将多个车辆多个需求地点放在一个系统中进行考虑，确定车辆的运输线路。车辆调度问题实质上是个复杂的组织优化问题，求解的基本方法可分为精确算法和启发式法两大类:精确算法指可以精确地求出最优解的算法，计算量随着问题规模的增大呈指数增长，因此其实际应用范围受到了一定的限制，所以专家们主要研究的是高质量的启发式算法，目前的主要算法有粒子群算法、蚁群算法等。

本文采用基于模型的预先优化法，根据配送中心和多个配送点，使用蚂蚁算法，用matlab软件仿真出最短路径。运送时，配送车辆可以根据预先优化的最短路径进行无返回一站式运输；并且可以根据当时的路况信息和配送货物量自动选择车辆进行区域式的运输方式，实现车辆动态调度。

1 车辆调度数学模型的建立

不失一般性，设整个蚁群中的蚂蚁数量为m，所需访问的配送点的数量为n，城市i与城市j之间的距离为dij（i，j＝1，2，…，n），在t时刻配送点i和配送点j连接路径上的信息素浓度为τij（t）。初始时刻，各个城市间连接路径上的信息素浓度相同，不妨设τij（t）＝0。

蚂蚁k（k＝1，2，…，m）根据各个城市间连接路径上的信息素浓度决定选择下一步要转移的配送点，设为t时刻蚂蚁k从配送点i转移到城市j的概率，其计算式为

式中:ηij（t）为启发函数，ηij＝1／dij为蚂蚁从配送点i转移到配送点j的期望程度。allowedk（k＝1，2，…，m）为蚂蚁k下一步被允许访问的配送点的集合，参数m即为蚁群系统中蚂蚁的数量，文中，令它等于配送地点的数量。开始时，allowedk中有（n－1）个元素，即包括除了蚂蚁k出发的配送点的其他所有配送点，随着时间的推进，allowedk中的元素不断减少，直至为空，即表示所有城市均访问完毕。信息启发因子α代表蚂蚁在运动过程中积累的信息素，α取值范围为1～2.5，系统中α取值为1。期望启发因子β表达了蚂蚁在选择路径时相对重要程度，β一般取值范围为1.5～5，系统中β的取值为5。

在蚂蚁释放信息素的同时，为了不让蚂蚁选择已经访问过的城市，采用禁忌表来记录蚂蚁k当前所走过的城市，各个城市间连接路径上的信息素逐渐消失。经过t时刻，所有蚂蚁都完成一次周游，计算每只蚂蚁所走过的路径长度，并保存最短的路径长度，同时，更新各边上的信息素。运算式为

式中:Δτkij为第k只蚂蚁在城市i与城市j连接路径上释放信息素浓度；Δτij为所有蚂蚁在城市i与城市j连接路径上释放的信息素和浓度之和。参数p反映了路径信息素的衰减系数（亦挥发系数和蒸发系数），而1－p则反映了信息的残留量，及持久性系数。信息残留因子的最佳值应该处于0.4～1.0，本系统中p值取0.5。

针对蚂蚁释放信息素问题，一般选用Antcycle System模型计算释放的信息素浓度，及蚂蚁经过的路径越短，释放的信息素浓度越高，其Δτij的计算式如下:

式中:Q为常数，表示蚂蚁循环一次所释放的信息素总量，即信息素释放强度，在本文系统中，Q＝100；Lk为第k只蚂蚁经过路径的长度。

2 数值仿真

如图1为某配送站需配送地点详图，配送中心位于坐标星号处，横坐标向东为正，纵坐标向南为负，而各数字所标明的地点为22个配送地点，配送中心为配送地编号1，该配送中心坐标为（390，－265），各配送地点坐标如表1所示，坐标原点如图1所示。

基于蚁群算法原理，解决上述问题一般需要以下几个步骤，如图2所示。

图1 某配送站需配送地点详图

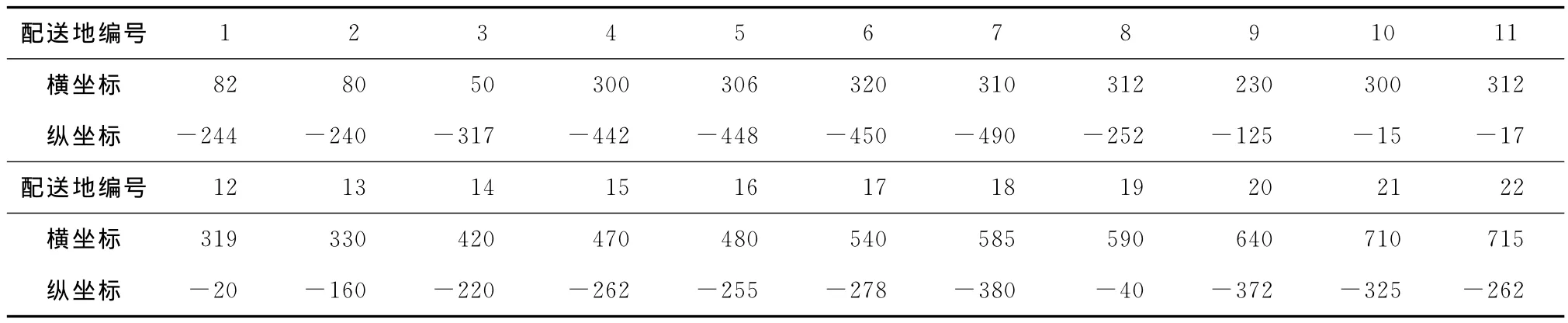
表1 各配送地点坐标

图2 蚁群算法原理步骤

1）初始化各参数。计算时，需要对相关的参数进行初始化，如果蚁群的规模（蚂蚁数量）m、信息素重要程度因子α、启发函数重要程度因子β、信息素挥发因子p、信息素释放总量Q、最大迭代次数和迭代次数初值。

2）构建解空间。将各个蚂蚁放置于不同出发点，对每个蚂蚁k（k＝1，2，…，m），按照第一个概率函数计算其下一个待访问的配送点，直到所有蚂蚁访问完所有配送点。

3）记录本次迭代最佳路径。

4）计算各个蚂蚁经过的路径长度Lk（k＝1，2，…，m），记录当前迭代次数中的最优解，即是所求的最短路径。

5）根据信息素浓度更新Δτkij计算式。

6）判断是否终止。若iter＜iter＿max，令iter＝iter＋1，清空蚂蚁经过的记录表，并返回步骤2）；否则，终止计算。

7）结果输出与结果分析。用一辆车进行配送，根据现实环境，会出现路况堵塞或是配送量较大等情况。当路况堵塞时，排在后面的配送点不能够及时收到货物，或是配送量较大时，一辆货车不能够装载足够的货物。这里，需要采用3辆车的配送方式。

运用上述运算方法进行多辆车分区域路径优化，各个蚂蚁仍然均以配送中心为起始点进行最短路径迭代。为了更直观的对结果进行观察和分析，以图形的形式将最短路径的配送顺序显示出来。如图3所示，3辆车配送的路径优化，如图4所示，3辆车各自的最短路程和平均路径。

图3 3辆车配送最短路径仿真示意

图4 3辆车配送最短路径与平均路径示意

由仿真线路图和最短路径迭代显示来看:

当采取3辆车的配送方式，系统将配送点分为三个部分，进行分区域的3辆车的配送方式。

第1辆车的配送路线为:配送地1→配送地5→配送地6→ 配送地7→ 配送地8→配送地4→ 配送地2→ 配送地3→ 配送地9→ 配送地1。

配送的最短距离为:970.286 1km

第2辆车的配送路线为:配送地1→ 配送地14→ 配送地10→ 配送地11→ 配送地12→ 配送地13→ 配送地20→ 配送地15→ 配送地1。

配送的最短距离为:950.456 0km

第3辆车的配送路线为:配送地1→ 配送地16→ 配送地17→ 配送地18→ 配送地23→ 配送地22→ 配送地21→ 配送地19→ 配送地1。

配送的最短距离为:761.726 4km

所以，两辆车配送最短路径总长度为2.682 5×103km。

3 结 语

本文采用无返回式的一站式运输，保证最短路径的同时，大大提高了运输效率，节约了运输时间和运输成本。并且根据路况信息，选择多辆车的分区域运输方式，完成动态调度，在保证路况信息的同时，更合理地完成配送。

［1］吴斌，倪卫红，樊树海等.放式动态网络车辆路径问题的粒子 群 算 法 ［J］.计 算 机 集 成 制 造 系 统，2009，15:1788－1794.

［2］段海滨.蚁群原理算法及其应用［M］.北京:科学出版社，2005:12－35.

［3］马良，朱刚，宁爱兵.蚁群优化算法［M］.北京:科学出版社，2008:2.

［4］吴斌，邵建峰，方叶祥，等.基于客户满意度的开放式车辆路径 问 题 研 究 ［J］.计 算 机 工 程，2009，35（17）:193－194，197.

［5］刘冉，江志斌，耿娜，刘天堂.半开放式多车场车辆路径问题［J］.上海交通大学学报，2010（11）:1539－1545.

［6］王洪雪，雷黎黎.集装箱堆场箱位最优分配［J］.交通科技与经济，2013，15（1）:50－53.

［7］周佳，沈岩，夏宇，等.智能交通最短路径Dijkstra模糊动态方法分析［J］.交通科技与经济，2014，16（4）:9－12.