基于回归分析的卫星测高布格重力异常求取
胡桢干,张春灌,任祖松 刘超,何永清
(西安石油大学地球科学与工程学院,陕西 西安710065)
20世纪80年代初,卫星测高重力异常分辨能力达到30~40km,开始应用于难以开展实测工作的海洋地质构造研究,尤其是板块构造与盆地构造研究[1]。20世纪90年代以后,美国与英国都进一步研究与提高了卫星测高重力的分辨力,基本达到了20km,卫星测高重力被石油公司用于海洋油气快速普查与早期评价,一些盆地的应用取得了较好的地质效果[1-2]。21世纪初,卫星测高重力的分辨力已经达到15km,目前,卫星测高重力异常的分辨力已经接近10~8km和4×10-5m/s2的观测精度,已经用于中等比例尺的海洋地质与资源调查[1,3-5]。下面,笔者在对重力资料精度要求不高的情况下,基于一元线性回归分析方法,对船测布格重力异常和卫星测高自由空气重力异常进行了回归分析,获得了回归方程,进而利用回归方程计算了卫星测高布格重力异常。
1 问题的提出
卫星对地观测当前主要是海洋卫星测高技术[6]。由于水对雷达频域中的微波脉冲具有良好的反射性,所以卫星测高技术特别适用于海洋,能用于确定海洋大地水准面和海洋重力异常,目前尚不能应用于陆地。海洋卫星测高技术是利用星载雷达测高仪向海面发射脉冲信号,经海面反射后由卫星接收,根据卫星的轨道位置并考虑到海潮、海流、海风、海水盐度及大气压等因素的影响,推求海洋大地水准面高[7-9]。根据卫星的轨道位置推算出的海洋大地水准面高,它具有较高的分辨率,可根据重力场理论计算得到自由空气重力异常,再进行相关的改正,可得到相应的布格重力异常[1,10]。
对于近海,许多国家都开展了精度相对较高的船测重力测量工作。而对于离岸相对较远的海域,由于受政治争端等各种条件的影响,船测重力测量工作很难开展或者无法开展,这种情况下,可选择利用卫星测高数据计算重力异常。相对于卫星测高布格重力异常,卫星测高自由空气重力异常相对容易获得。由自由空气重力异常计算布格重力异常过程中,海水校正相对复杂。对于海底地形起伏较小的情况下,可以研究已知海域船测布格重力异常和卫星测高自由空气重力异常间的相关性,利用一元线性回归分析方法计算出预测方程,进而求取未知海域的卫星测高布格重力异常。
2 一元线性回归分析方法原理
回归分析中,只包括一个自变量和一个因变量,且2者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。一元线性回归分析是研究2个变量的线性相关性,它不仅可以说明2个变量是否一起变化,还可以计算出预测方程以预计这2个变量是如何一起变化的[11-12]。预测方程的形式为:

方程(1)通常叫作回归方程。其中,y为因变量;x为自变量;a是常数项;b是一元回归系数。
一般,线性回归都可以通过最小二乘法求出其方程:

式中,n为样本数;Xi、Yi、、分别为2个变量的观测值和均值。若b>0,表明2变量是正相关;若b<0,表明2变量是负相关。

图1 海底地形图 (图中数字单位:m)

图3 卫星测高自由空气重力异常图 (图中数字单位:10-5 m/s2)
3 卫星测高布格重力异常的计算
选取黄海海域青岛东部地区作为研究区域,海底地形起伏见图1,已知船测布格重力资料范围见图2,卫星测高自由空气重力异常见图3。由图1可见,自西向东,该区海域海水逐渐变深,但是海底起伏变化相对较平缓。由于研究区东部海域处于中国和韩国的争议海域,因此没有收集到该区域的船测重力数据。虽然船测布格重力异常 (见图2)和卫星测高自由空气重力异常 (见图3)值大小不等,但是异常的走向、梯度变化、高低起伏等特征宏观上一致,只是局部异常变化有些差异。
对比收集到的1747个船测布格重力异常数据和相对应的卫星测高自由空气重力异常数据,两者之间存在明显的线性关系(见图4)。对这些布格重力数据和自由空气重力数据进行一元线性回归分析,获得了如下回归方程:

式中,y为布格重力异常值;x为自由空气重力异常值。
根据上述回归方程,笔者计算了研究区东部海域的布格重力异常,这里称为卫星测高布格重力异常。利用该区西部海域的船测布格重力数据和东部海域卫星测高布格重力数据,编制了研究区布格重力异常图(见图5)。由图5可见,船测布格重力资料和卫星测高布格重力资料的数据拼接处,并不存在明显的南北向的异常同向扭曲、异常梯度变化带等数据拼接中常见的拼接问题,说明数据拼接效果良好,在另一方面也说明利用上述回归方程计算的卫星测高布格重力异常没有问题。
4 结语
自20世纪80年代以来,海洋卫星测高技术快速的发展,使得卫星测高重力异常分辨力及精度得到了很大的提高,已经可用于中等比例尺的海洋地质与资源调查。鉴于目前的海洋测高技术以及各种重力改正技术,卫星测高布格重力异常的分辨力及能力很难获得更大的提高。在海底地形起伏变化不大时,研究已知海域船测布格重力异常和卫星测高自由空气重力异常间的相关性,利用一元线性回归分析方法计算出预测方程,进而求取相邻未知海域的卫星测高布格重力异常,能满足中等或者小比例尺的海洋地质与资源调查。
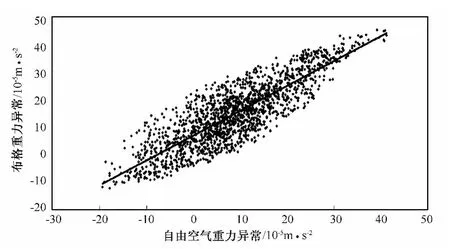
图4 回归分析图

图5 布格重力异常图 (图中数字单位:10-5 m/s2)
[1]张明华,张家强 .现代卫星测高重力异常分辨能力分析及在海洋资源调查中应用 [J].物探与化探,2005,29(4):295-298.
[2]王懋基,宋正范,尹春霞 .南海卫星重力研究 [J].物探与化探,1998,22(5):329-335.
[3]姚运生,姜卫平,晁定波 .南海海盆重力异常场特征及构造演化 [J].大地构造与成矿学,2001,25(1):46-54.
[4]许惠平,刘万崧,周云轩,等 .卫星测高重力资料及其在南海莺-琼盆地中的应用 [J].吉林大学学报 (地球科学版),2003,33(3):368-371.
[5]Chatterjee S,Bhattacharyya R,Majumdar T J.Utilization of high resolution satellite gravity over the Carlsberg Ridge[J].Mar Geophys Res,2007,28:309-317.
[6]宁津生 .卫星重力探测技术与地球重力场研究 [J].大地测量与地球动力学,2002,22(1):1-5.
[7]曾华霖 .重力场与重力勘探 [M].北京:地质出版社,2005.
[8]孙和平,周江存,彭碧波 .确定卫星重力场中的海潮负荷影响问题 [J].地球科学进展,2006,21(5):482-486.
[9]周江存,孙和平 .海潮对卫星重力场恢复的影响 [J].地球物理学报,2007,50(1):115-120.
[10]Bhattacharyya R,Majumdar T J.Residual geoid and free-air gravity over the Indian offshore from ERS-1high resolution altimeter data[J].Journal of the Indian Society of Remote Sensing,2006,34 (3):289-298.
[11]张明华,乔计花,黄金明,等 .重磁电数据处理解释软件:RGIS[M].北京:地质出版社,2011.
[12]张春灌,张明华,安玉林 .青藏高原重力异常与地形高程的负相关校正 [J].物探与化探,2007,31(3):236-238.

