逆向累积分布图及其在疫苗免疫原性数据分析中的应用

东南大学流行病与卫生统计学系（210009） 陈召青 王诗远 杨舒静 刘 沛

逆向累积分布图及其在疫苗免疫原性数据分析中的应用

东南大学流行病与卫生统计学系（210009） 陈召青 王诗远 杨舒静 刘 沛△

在疫苗临床试验中，接种后血清抗体水平的高低与该疫苗能否产生保护作用及保护水平的高低有着直接关系，因此对免疫原性的分析是疫苗临床试验统计分析的重要部分。就体液免疫反应而言，这类数据的一个重要特征是数据的取值范围较大，变化范围常跨越多个数量级，观察值间呈现倍数关系。虽然其原始观测数值呈右偏态分布［1］，但经对数转换后，免疫原性值一般满足正态或近似正态分布。对这类数据，目前国内通用的方法是首先计算其描述性统计指标如几何均数和对数标准差，而后对经对数变换后的数据采用假设检验和区间估计等方法进行统计推断［1-2］。这些方法虽然行之有效，但其结果表达方式均为在特定点（如几何均数）和较抽象的范围（如95%可信区间）表达其临床试验结果，这样一方面使研究工作者难以从体液免疫原性的整体数据变化上（如不同滴度的抗体水平上）把握数据的变化趋势和分布状况，另一方面也使非统计工作者难以理解一些组间比较的假设检验结果。为解决这些问题，Reed、Meade和Steinhoff于1995年提出了逆向累积分布图（reverse cumulative distribution，RCD）的概念和方法，这一方法因具有结果表达直观、传达信息量大等优点，一经提出就受到了疫苗临床试验工作者的青睐并在国外得到了较广泛的应用［3］。然而国内对此法却少有介绍，本文将从概念、方法及应用实例上对这一数据表达方式进行介绍。

原理与方法

逆向累积分布图（以下简称RCD曲线）是用来显示免疫原性数据分布的图形工具，特别适合于疫苗组间分布的可视性图形比较。该图的横轴为经过对数转换后的抗体滴度或浓度，纵轴代表至少有此抗体水平个体所占百分比。根据定义，图中的曲线从100%开始，然后从左到右逐渐下降至0，曲线最低点就是抗体水平最大时的观察者比例。逆向累积分布函数的表达形式为

式（1）中Rx（x）表示变量X大于等于某一数值x的概率。而通常的累积分布函数为

式（2）中Cx（x）表示变量X小于等于其某一数值x的概率。由此可知，逆向累积分布图之所以被称为逆向，是因为它是累积分布图（cumulative distribution plot）的逆转。而正是这一逆转，使得它特别适合于对疫苗免疫原性数据的直观表达［4-5］。

与逆向累积分布图相似的是Kaplan-Meier生存曲线（survival curve），只不过生存曲线多以生存时间为横轴、生存率为纵轴，随着生存时间的递增，生存率曲线从1到0逐渐下降，与逆向累积分布图不同的是它不是一条平滑的曲线，而是阶梯状逐渐下降的图形［2］。

绘制RCD曲线时，首先要根据每一抗体水平在y轴上找出至少有此抗体水平个体所占的百分比，然后将这些点用折线连接起来。第一个绘制的点通常表示在最低抗体水平下个体所占的百分比，一般为100%。曲线从左至右，x值越来越大，y值越来越小，最后会无限接近于0。利用RCD曲线可以估计各种百分位数，如求第50分位数所对应的抗体滴度对数值，就可在y轴上找到50%，画一条水平线与曲线相交，然后再找出交点所对应x轴上的值，就是所求值，即中位抗体滴度的对数值。另外，通过已知x值也可求得y值，这一般用于已知保护水平或最低检测限估计观察对象所占的累积百分比［3］。

图1给出了四条颇具代表性的RCD曲线。大部分RCD曲线是倒S型，如曲线D，直到在x轴上到达某一数值时迅速下降至最小值。曲线A呈现近似直角形，开始保持高且平坦，直到一个在横轴上达到较大数值时迅速下降至最小值，表示抗体水平较高者所占比例较大。如果曲线以一条相对直的斜线降到x轴如曲线C，说明抗体滴度的变异较大。曲线的陡峭程度反映了观察值的伸展程度和变异性。中部和尾部一样陡，说明较少的变异，而此时曲线C比较浅的中部表示较大的伸展性和变异性。在极端的例子中，RCD曲线以垂直的曲线结束，说明数据集中，几乎没有变异，所有余下的数据都相等［3］。曲线B比曲线C陡峭，但是又不及曲线D，表示其变异性比曲线D大，但又小于曲线C。曲线B和曲线C相交，两者有一个相同的百分位值，如图1中，该点为当抗体滴度对数转换值为6时，累积频率百分比为40%，在小于抗体水平6时，B组更占优势，但是超过6时，C组就更占优势了。

图1 逆向累积分布图

实例分析

我们以肠道病毒71型灭活疫苗（Vero细胞）做试验组和安慰剂做对照组进行的III期临床试验为例说明RCD曲线和目前通用的统计描述和统计推断方法相结合，以提高统计结果形象化和增加数据信息量之效果。研究人群按发病特征分成6～11月龄和12～35月龄两层。

从表1我们可以看出在肠道病毒71型（EV71）疫苗组免疫前后经配对t检验t＝60.92，P＜0.0001，差异有统计学意义，所以可认为试验组疫苗在免疫前后抗体水平不同，提示EV71疫苗对健康人群可能有保护作用；安慰剂组经配对t检验t＝-2.34，P＝ 0.0194，差异有统计学意义，所以安慰剂组在免疫前后抗体水平也不同。从表1我们还可以看出免疫前EV71疫苗组和安慰剂组经过两样本t检验t＝-0.51，P＝0.6103，P＞0.05，差异没有统计学意义，所以尚不能认为在免疫前后两组疫苗的受试者抗体水平不同；免疫后EV71疫苗组和安慰剂组同样经过两样本t检验t＝30.73，P＜0.0001，差异有统计学意义，所以可以认为在免疫前后两组疫苗的受试者抗体水平不同。面对上述统计分析结果，有时难以使人一下子得到试验疫苗是否有效的清晰结论。此时借助RCD曲线（图2）不但可增加统计结果的直观性，方便理解，而且可有效把握数据的变化趋势和分布状况。由图2可知，免疫前试验组和免疫前后安慰剂组的曲线，在抗体水平较小时就迅速下降，说明试验组免疫前以及安慰剂组免疫前后抗体水平都较低，而免疫后试验组曲线开始保持高而且平坦，直到达到一个在横轴上较大数值时才下降，表示试验组免疫后抗体水平较高者所占比例较大，安慰剂组免疫前后抗体水平变化不大，这也说明了虽然安慰剂组统计分析结果有意义（P＝0.0194），但是实际意义不大，从而从实际角度直观地解释了表1中一系列（4个）假设检验结果的实际意义。

表1 两试验组抗体滴度免疫前后结果比较

图2 不同组别抗体滴度逆向累积分布图

随着分组数的增加，假设检验的数量也成倍增长，对统计检验结果的综合分析和判断也更趋抽象，此时RCD曲线的优势则更为明显。如在本次试验中每组疫苗又分成两个年龄层，为得出试验结论，需要在八个组中进行比较。从表2我们可以看出免疫前两个年龄组6～11月龄和12～35月龄中试验组和安慰剂组P值分别0.4696和0.7641，差异无统计学意义。免疫后两个年龄组中试验组和安慰剂组P值都小于0.0001，差异有统计学意义。在6～11月龄中EV71疫苗组免疫前后经配对t检验t＝-36.31，P＜0.0001，差异有统计学意义，所以可认为6～11月龄试验组疫苗在免疫前后抗体水平不同，安慰剂组免疫前后配对t检验t＝0.32，P＝0.7458，差异没有统计学意义，所以尚不能认为6～11月龄安慰剂组在免疫前后抗体水平不同；在12～35月龄中EV71疫苗组免疫前后经配对t检验t＝-50.31，P＜0.0001，差异有统计学意义，所以可认为12～35月龄试验组疫苗在免疫前后抗体水平不同，安慰剂组免疫前后配对t检验t＝-2.59，P＝0.0099，差异有统计学意义，所以12～35月龄安慰剂组在免疫前后抗体水平也不同。

表2 不同年龄层两试验组抗体滴度结果比较

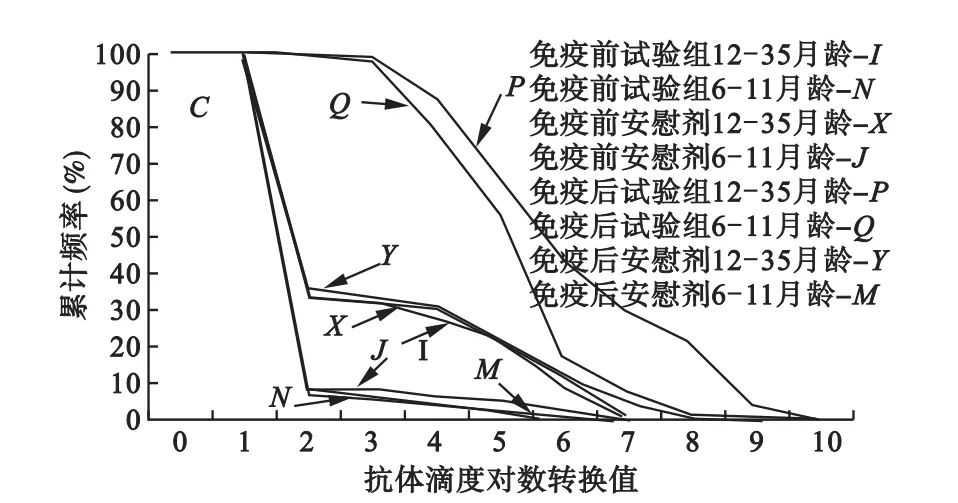
图3 不同组别不同年龄层抗体滴度逆向累积分布图

图3描述的是两组疫苗两个年龄层在免疫接种前后抗体滴度的RCD曲线图，经过观察我们可以明显看出免疫后试验组12～35月龄和6～11月龄的曲线（曲线P和Q）形状与位置与其他曲线不同，其他曲线在抗体滴度较小时就迅速下降，而曲线P和Q开始保持高而平坦，在抗体滴度较大时才开始下降，说明两个年龄组免疫后EV71疫苗组较高抗体水平者比例较大。同时曲线N、J和M有着多处交叉，三者总体的形状和位置基本一样，说明6～11月龄受试者在接种前试验组和对照组抗体水平无差异，并且接种了安慰剂之后抗体水平未见变化。同样的情况也发生在曲线I、X和Y中，表示12～35月龄与6～11月龄组结果基本相似，虽然接种了安慰剂之后统计检验结果显示抗体水平有变化（t＝2.59，P＝0.0099），但从图3可见，其变化幅度较小，提示其实际意义有限。所以通过解读图3，我们发现RCD曲线图不仅可以直观地解释表2中一系列（8个）假设检验结果的意义，让非统计人员更容易理解，而且还能形象说明统计检验结果的实际意义。

讨 论

本文介绍了逆向累积分布图的概念、制作方法及其在疫苗III期临床试验中的应用。我们可以看出逆向累积分布图不仅增大了信息量，结果直观，而且具有绘制简单、易于非统计人员理解的优点，特别适合对疫苗免疫原性数据的表达。在绘制过程中需要注意的是，曲线上的点表示的是至少有此抗体水平个体所占的百分比，所以计算方法是先通过每一个抗体水平个体所占百分比计算出正向累积百分比，然后再算出其逆向累积百分比绘制图形。另外，逆向累积分布图不能提供准确数据信息，因此需要和相应的统计指标和假设检验方法同时使用，而这些信息常通过统计表的形式表达。通过图表结合，我们不仅可以准确的表达数据信息，而且可以使一些抽象的统计结果直观化，有利于我们从整体上把握数据蕴含的信息。建议在免疫原性数据统计分析结果表达中将传统的统计指标描述和统计假设检验与RCD曲线图示法相结合，以取得相互补充、相得益彰之效果。

1.方积乾.卫生统计学.第6版.北京：人民卫生出版社，2008.

2.孙振球.医学统计学.第3版.北京：人民卫生出版社，2010.

3.Reed GF，Meade BD，Steinhoff MC.The reverse cumulative distribution plot：A graphicmethod for exploratory analysis of antibody data.Pediatrics，1995：600-603.Jozef Nauta.Statistics in Clinical Vaccine Trials. New York：Springer，2010：19-52.

4.Edward KM，Meade BD，Decker MD，et al.Comparison of 13 acellular pertussis vaccines：overview and serologic response.Pediatrics.1995：548-557.

5.Horne AD.The Statistical Analysis of Immunognicity Data in Vaccine atials.New York：Annals of the New York Academy of Sciences，2006：2211-2215.

（责任编辑：丁海龙）

△通信作者：刘沛