基于磁共振技术的生物电阻抗成像研究进展

陈 会 闫丹丹

基于磁共振技术的生物电阻抗成像研究进展

陈 会 闫丹丹

磁共振电阻抗成像（magnetic resonance electrical impedance tomography, MREIT）是将MRI与电阻抗成像（electrical impedance tomography, EIT）技术相结合，通过MRI系统测量成像体内部的磁通密度值对成像体的电导率图像进行重建，是无创性地进行阻抗成像的一种新方法。MREIT由Zhang[1]于1992年首次提出，其基本方法是利用物体内的电流密度分布和磁感应强度测量值来重构物体内电导率的分布。传统的EIT需测量多个边界电压值来提高重建图像的精确度与空间分辨率，但求解过程值不稳定，利用磁感应强度进行重构图像能够解决此缺陷。本文拟对MREIT的最新研究作一综述。

1 MREIT的原理

MREIT通过表面电极将电流注入物体中，由MRI扫描仪检测到注入电流引起的电磁场变化，根据电磁场的变化运用安培定律求得电流密度，已知电流密度和磁感应强度可以利用MREIT算法重构出物体的电阻抗分布。它有效地解决了传统EIT边界测量值对物体内部电阻率变化不敏感的问题，得到物体高分辨率、高精确度的电阻率分布图，系统框图见图1。

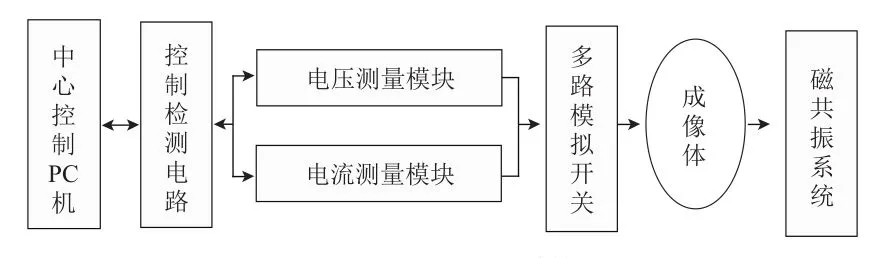
图1 MREIT系统

将成像物体置入MRI扫描仪中，通过表面电极注入与MRI时序相匹配的电流，此电流在物体内部产生的电流密度会在物体周围及内部产生电磁场。该电磁场平行于MRI主磁场的分量可以通过MRI扫描仪进行测量，将物体进行三维旋转，则可以得到电磁场的3个分量Bx、By和Bz。运用安培定律得到物体内部的电流密度分布Jx、Jy、Jz，可以根据电流密度分布和物体内部电导率分布对电阻抗分布进行逆问题重建。电阻抗重构可以分为正问题和逆问题两种。

1.1 正问题描述 正问题根据已知电阻抗的分布和注入电流边界条件求得由内部电流引起的磁感应强度，它为逆问题提供数据并验证所提出的算法。MREIT正问题用泊松方程表述，见公式（1）及公式（2）。

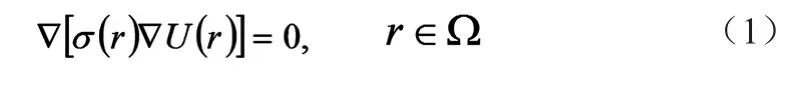
其中U(r)为物体内电势分布，σ(r)为物体内电导率，Ω为所要成像的三维物体，n为方向向量。得到物体内部电势分布U(r)，则利用公式（3）及公式（4）求得电场强度E和电流密度J。

根据Biot-Savat定律求得物体内磁感应强度分布，见公式（5）。

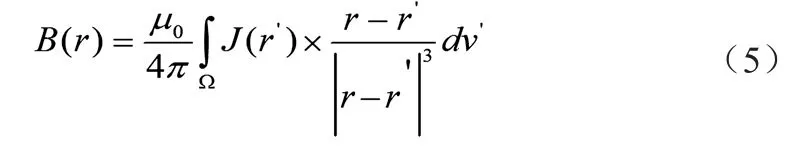
其中μ0为真空磁导率，B(r)为磁感应强度。

1.2 逆问题描述 重构三维物体内部未知的电导率分布，通过对正问题的描述可以得到适当的边界条件下物体内部的电场分布，逆问题求解需要建立电导率分布关系，并根据此关系反解出电导率的分布。MREIT逆问题可以根据物体内部电流密度J或磁感应强度B分布，对物体内部电阻抗（电导率）的分布进行重构，因此MREIT的成像算法分为基于电流密度的重建算法和磁感应强度的重建算法。目前研究热点多是获得磁感应强度进行电导率重构。

运用磁感应强度分布对电导率进行重建获取的信息量相对较多，因此成像分辨率和精确度较高，但在实际操作过程中要对成像物体进行三维旋转获得3个方向的磁感应强度难以实现。利用电流密度分布对电导率重建获取信息相对较少，成像精确度不高，空间分辨率低。

1.3 MREIT的研究方向 在生物医学工程领域中，MREIT是重要的分支和研究热点。韩国、英国、土耳其、加拿大等国家都在进行研究，中国起步相对较晚。根据MREIT发展状况来看，主要研究方向见图2。

2 MREIT算法的研究

2.1 基于电流密度的算法 基于电流密度分布对物体内部电导率分布进行重建的算法，首先对外加注入电流引起的磁场分布的3个分量进行测量，然后利用安培定律对物体内部的电流密度进行求解，最后利用电流密度、边界电压关系对物体内部电导率分布进行重建。

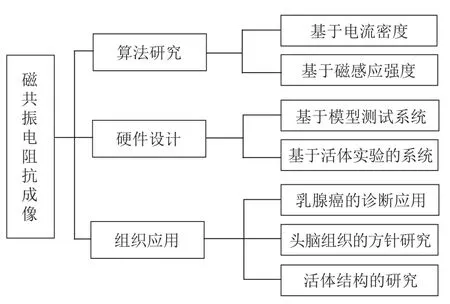
图2 MREIT的发展状况

基于电流密度的MREIT算法包括：①求解电导率分布的MREIT算法，其基本思想是最小化测量的电流密度J与通过正问题求解的电流密度J*之间的差得到求解电导率的迭代方法；②基于非线性偏微分方程的J-Substitution算法，利用内部电流密度来重构静态的截面阻抗图像；③由于J-Substitution算法要求解非线性偏微分方程，故提出另一种求解物体内真实电导率分布的MREIT算法——基于等势线的非迭代MREIT算法，即利用物体内电流密度分布与边界电压测量值来重建阻抗图像，其内涵与J-Substitution算法类似。

J-Substitution算法的思想是计算出每个有限单元的电流密度分布值与电流密度测量分布值之差最小，即目标函数定义为公式（6）。

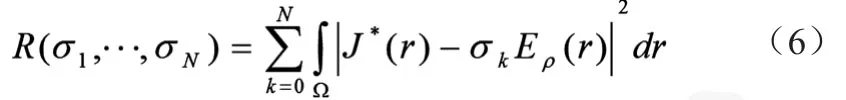
Eyüboglu等[2]和Kwon等[3]分别提出了基于等势线的MREIT算法，将电流密度进行分解，求出物体内的电场分布，这种算法可以得到分辨率和精确度很高的重建电导率分布图，收敛性良好；但其是在二维基础上建立起来的算法，推广到三维成像不精确。2005年，Ozparlak等[4]采用基于单方向磁感应强度测量的感应电流成像方式的重构算法，该方法使残留的主磁场经过拉普拉斯运算后进一步减弱，减少了重建时间，加快了成像速度。2013年，Park等[5]使用快速梯度脉冲回波序列最大化测量Bz数据，并在短时间内读取物体内部电流变化，直接测量2Bz来代替Bz获得k-空间数据，避免了繁琐的展开过程。

2.2 基于磁感应强度的算法 基于磁感应强度测量值对成像物体内部电导率进行重建的算法，先利用MRI扫描仪对注入电流引起的电磁场分布的一个分量进行测量，然后利用电磁场对物体内电导率的分布进行重建。

最初的磁感应强度主分量Bz的算法是Birgül等[6]于 1996年基于灵敏度矩阵提出的，其基于Bz和电导率的线性关系而建立，利用奇异值分解方法将灵敏度矩阵转化改进实现了MREIT的二维成像。迭代灵敏度算法实现重建图像是通过不断更新电导率分布函数使得磁通密度的计算值逐渐逼近测量值，当满足一定终止条件时即可以用当前电导率分布作为重构值。李刚等[7,8]将灵敏度矩阵算法推广到三维空间，通过分层与整体两种重建方式对比提出了改进后的分层重建算法，在对每个层面仅利用该层的磁通量密度测量值进行重建数据修正，降低了计算维数，使得到的数据更精准，有效地缩短了阻抗图像重建时间。

李小霞等[9]及Jeon等[10]通过表面注入电流产生电流J和磁感应强度B之间的物理关系建立MREIT的数学模型，结合截断奇异值正则化方法提出了MREIT的算法，采用新的偏微分方程对Bz数据进行去噪，改善了算法的不适定性，提高了重建图像的质量。巩玉香等[11]研究证实通过斜位电流注入增大了MRI的空间，提高了成像质量，并且验证了电阻抗分布正交各向异性的MREIT问题的唯一性。

Seo等[12]将单一磁场分量Bz的谐波算法与局部谐波Bz算法结合起来，有效避免了重建图像在低电导率区域成像模糊的问题。2003年，Oh等[13]对Seo提出的谐波Bz算法进行改进，利用2个注入电流测量得到的单个方向的磁感应强度，对物体内的电导率分布有效地进行了评估。刘阳等[14]将MREIT算法扩展到三维，利用单个磁感应强度测量值在多种脑组织球头模型进行仿真实验，避免了成像物体在MRI系统中的旋转问题，在复杂的三维脑组织成像算法方面取得进展。

Park等[15]于2004年提出了梯度Bz分解算法，该算法把所求区域分成多个薄层降低求导阶数，运算简便、抗噪能力强。在此基础上改进的算法典型包括调和Bz算法和局部调和Bz算法，不仅改善了不适定性，抗噪也得到提高。2005年，Sadleir等[16]在实验的基础上分析了MREIT系统中的噪声来源，研究了噪声对重构电流密度和电阻率的影响，提出了优化脉冲序列和信号平均的方法降低噪声水平。Xu[17]及Chen[18]基于怀柔算法提出了新的去噪技术，怀柔运算的核心是高斯卷积，通过Bz数据消除测量噪声，有效地重建出边界清晰的图像。2011年，Woo等[19]在phantom实验中采用测量单方向磁感应强度Bz测量值来重建图像，通过相位展开、几何误差校正等数据处理方法来提高图像的精确度。

2013年，Jeon等[20]给出了CoReHA2.0的软件包，包括MREIT体内试验的数据、二维图像识别区域、可对图像进行缩放、去噪、修复等各种工具，方便进行仿真、验证实验。该软件的建立推动了从二维到三维图像重建的发展。

目前对电阻抗图像重建主要集中在三维算法上，三维图像较二维图像更能直观地反映病变组织的存在及位置信息，但三维图像涉及更大的矩阵、存储空间和重建时间，因此需要更高的硬件来满足需求。

3 MREIT的硬件系统研究

随着医疗条件的改善，使用MRI设备获得高分辨率的生物电阻分布图方便可行。MRI的测量主要是主磁场方向的磁通量密度，以主磁场为轴向的MREIT系统的应用是研究热点。

既往研究实现了工作频率为10 MHz的生物组织仿真模型成像系统，补偿线圈有效地抵消了测量信号中的主磁场，提高了测量灵敏度，推进了磁感应断层成像理论在生物医学领域中的应用。利用磁阻抗成像的思想，即电极向物体表面注入电流，通过测量物体周围的磁场强度重构电流密度分布，Ireland等[21]提出磁探测电阻抗成像方式并建立实验系统，该系统在物体轴向注入电流，测量与中心轴垂直的平面内的磁场，实验中分别对电阻抗离散分布的物体、盐溶液和人体进行测量，利用反投影算法和灵敏度矩阵法重构出电流密度分布，进而重建出电阻抗分布图，该成像方法为无创生物电阻抗成像提供了一个新思路。

2011年，Kim等[22]对人体下肢进行成像，运用3T MRI扫描仪和四电极系统，在小腿和膝盖周围覆盖四碳棒水凝胶电极，选择了多对相反的电极注入电流方式重复试验，从0开始增加电流的幅值直到小腿疼痛阈值，记录疼痛的电流阈值数据，并在阈值范围内成功得到清晰的下肢重构图像。

Li等[8]在开放MRI系统上利用半球模型进行模拟实验，得到准确的重建图像。此外，该课题组采用三维圆柱模型和人体小腿磁共振图片的真实模型用以检验环形电极模式，环形电极模式仅利用竖直方向的磁场分量信息即对成像的电导率分布进行重建，验证了开放式MREIT系统具有普遍适用性。

2011年，Minhas等[23]设想了采用三维MREIT模拟器（MREITSim）模拟演示静态生物电阻抗成像，并把模拟用的k-空间数据应用到模拟器中，对于开发新的脉冲序列及精确的图像重建具有重要意义。随后，Sadleir等[24]建立连接心脏的逼真乳腺模型，运用3T MRI扫描仪和4通道线圈进行扫描，把不同生物组织应用在实验模型中，在评估监测细胞的癌变方面取得显著成果。

4 MREIT在不同组织中的应用

4.1 MREIT在乳腺癌中的应用 2011年，Kim等[22]构建逼真的三维乳腺癌模型，实验和数值模拟检测癌变组织，验证了注入电流＜1 mA可以重构图像的可行性。实验中运用的3T MRI扫描仪采用总宽度为28 ms的多回波脉冲序列和高性能射频线圈区分了重建图像＜1 mm的像素，成功区分猪肌肉和鸡肉的电导率值，最终将注入电流降低为0.7 mA。

2012年，Sajib等[25]在以NaCl、CuSO4、琼脂等材料制成的乳腺模型上进行模拟仿真，检测癌变的乳腺，阻抗重建图像可以有效地区分出病变组织与正常组织的微小差异。采用MRI扫描仪评估测量磁通量密度数据噪声水平，测量通过乳腺表面注入电流在心脏处产生电流密度的大小，得出最大电流密度在心脏区域远低于神经设定阈值的结论。

2013年，Sadleir等[24]通过限制心脏的最大电流密度使其低于神经兴奋的水平，在乳腺表面注入＜1 mA的电流诊断出直径＜5 mm的癌变区域，指出恶性肿瘤较正常组织具有更高的电导率，MREIT对乳腺癌的诊断提供独特的信息。

4.2 MREIT在头部组织的仿真研究 Yang等[26]通过四层球头模型和真实头模型对颅内病变组织电阻抗成像进行仿真研究，用MRI系统对人体头部进行三维构建和不同组织的边界区分，利用多种算法分别对均质和非均质颅内病变的模型进行重建，结果表明，MREIT对颅内病变组织（血肿或脑瘤）的阻抗成像过程简单，重构的阻抗图像精确性高，且算法具有一定的抗噪性能。

由于头部结构复杂，注入电流的大小、不同组织间相互干扰等仍然是研究的难题，尤其是颅骨的低电导率使成像更加困难。

4.3 MREIT在活体中的应用 作为一种无创检测手段，MREIT已经在理论、算法和实验技术方面得到迅速发展，并已经在动物和人体内进行实验。既往研究利用MREIT分别成功对活体和死亡小猪头部的电流密度分布测量进行阻抗重建，根据阻抗变化结果发现流入死亡小猪头部的电流值较正常小猪大大减少。

杨瑞霞[27]在患有癌症的白鼠体内进行MREIT实验，得到可以区分的正常组织和癌变组织的电导率分布图，但缺少具体的数据；随后，该课题组在10只患有癌症的白鼠上进行系列实验，获得的癌变组织与正常组织的电导率分布图具有明显差异，得出活体中癌变组织的电导率是正常组织的2～3倍。

2011年，Kim等[28]对人体下肢进行成像，运用单回波和多回波两种脉冲序列基于Dixon数据进行化学位移伪影校正，通过注入3 mA电流成功重构电导率图像，延长电流注入总时间来降低被测磁通量密度信号中的噪声，首次解决了化学位移伪影和Bz数据测量噪声的技术问题，提高电导率成像质量。此后，该课题组[22,25,28]再次运用Siemens 3.0T MRI扫描仪和多通道线圈，注入脉冲宽度为30 ms、幅值为0.5～3.0 mA的电流，成功检测到乳腺癌病灶。

2013年，Oh等[29]将MREIT技术运用到动物模型体内，以评估脑脓肿感应前后电导率随时间变化的特点，为脓肿病灶提供一个对比新信息，结果发现，脓肿病变与电导率的相对相关系数随诱导时间发生改变，中央脓肿病灶高于周边地区。超过12 h，诱导时间和相对电导率对比度先呈正相关后呈负相关。该研究通过电导率的恢复监测体内温度，初步证实温度和电导率呈高精度的线性关系。

5 结束语

近年来，MREIT不仅在图像重建算法方面得到优化和完善，随着软硬件技术的迅速发展，在组织模型和活体实验研究方面也以其独特的优势取得了重大突破，这将有助于疾病的临床诊断。然而，MREIT在重建算法的抗噪性和收敛性、电极系统的选取、注入电流幅值大小等方面仍需提高，尤其在活体实验方面仍需更多突破。

生物阻抗的变化与其生理和病理状态密切相关，MRI检查能够显示病变组织的部位、大小和范围，具有较高的空间分辨率和对比灵敏度[30]，将电阻抗与MRI相结合的功能成像方式可以检测出已发生病变但未表现出病变特征的组织，为疾病的诊断及治疗提供更早、更有效的信息。参考文献

[1] Zhang N. Electrical impedance tomography based on current density imaging. Toronto: Msc Thesis University of Toronto, 1992.

[2] Eyüboglu BM, Reddy R, Leigh JS. Magnetic resonance electrical impedance tomography: 21st Annual Conference and the 1999 Annual Fall Meeting of the Biomedical Engineering Society. Atlanta: IEEE, 1999: 1127.

[3] Kwon O, Lee JY, Yoon JR. Equipotential line method for magnetic resonance electrical impedance tomography. Inverse Problem, 2002, 18: 1089-1100.

[4] Ozparlak L, Ider YZ. Induced current magnetic resonanceelectrical impedance tomography. Physiol Meas, 2005, 26(2, SI): S289-S305.

[5] Park C, Kwon OI. Current density imaging using directly measured harmonic Bz data in MREIT. Comput Math Methods Med, 2013, 2013: 381507.

[6] Birgül Ö, Ider YZ. Electrical impedance tomography suing the magnetic field generated by injected currents: 18th Annual international conference of the IEEE Engineering in Medicine and Biology Society. Amsterdam: IEEE, 1996: 784-785.

[7] 李刚, 陈瑞娟, 郝丽玲, 等. 三维磁共振电阻抗成像的改进分层灵敏度算法. 计算物理, 2012, 29(6): 845-852.

[8] Li G, Chen RJ, Hao LL, et al. Three dimensional MREIT for breast cancer detection on open MRI scanners. Information and Automation (ICIA), 2012, 33(10): 446-450.

[9] 李小霞, 王泽文, 何碧琴. 基于偏微分方程去躁的磁共振电阻抗成像. 东华理工大学学报(自然科学版), 2012, 35(1): 94-100.

[10] Jeon K, Kim HJ, Lee CO, et al. Integration of the denoising, inpainting and local harmonic B(z) algorithm for MREIT imaging of intact animals. Phys Med Biol, 2010, 55(24): 7541-7556.

[11] 巩玉香, 王慧贤, 王玉宇, 等. 斜位电流注入磁共振电阻抗成像(MREIT)与硬件设计. 波谱学杂志, 2007, 24(2): 183-189.

[12] Seo JK, Yoon JR, Woo EJ, et al. Reconstruction of conductivity and current density images using only one component of magnetic feld measurements. IEEE Trans Biomed Eng, 2003, 50(9): 1121-1124.

[13] Oh SH, Lee BI, Woo EJ, et al. Conductivity and current density image Reconstruction using harmonic Bz algorithm in magnetic resonance electrical impedance tomography. Phys Med Biol, 2003, 48(19): 3101-3116.

[14] 刘阳, 吴占雄, 朱善安, 等. 各向异性头部组织感应电流磁共振电阻抗成像. 浙江大学学报(工学版), 2011, 45(1): 168-172.

[15] Park C, Kwon O, Woo EJ, et al. Electrical conductivity imaging using gradient B, decomposition algorithm in magnetic resonance electrical impedance tomography (MREIT). IEEE Trans Med Imaging, 2004, 23(3): 388-394.

[16] Sadleir R, Grant S, Zhang SU, et al. Noise analysis in magnetic resonance electrical impedance tomography at 3 and 11 T field strengths. Physiol Meas, 2005, 26(5): 875-884.

[17] Xu HL. A new denoising technique in magnetic resonance electrical impedance tomography: 2011 Fourth (BMEI). Shanghai: IEEE, 2011: 38-41.

[18] Chen Q. Reconstruction of conductivity based on radial basis functions in MREIT: 2011 Fourth International Conference on Information and Computing. Phuket Island: IEEE, 2011: 122-125.

[19] Woo EJ. High-resolution MREIT using low imaging currents: 33rd Annual International Conference of the IEEE EMBS. Boston: IEEE, 2011: 7025-7028.

[20] Jeon K, Lee CO. CoReHA 2.0: a software package for in vivo MREIT experiments. Comput Math Methods Med, 2013, 2013: 941745.

[21] Ireland RH, Tozer JC, Barker AT, et al. Towards magnetic detection electrical impedance tomography: data acquisition and image Reconstruction of current density in phantoms and in vivo. Physiol Meas, 2004, 25(3): 775-796.

[22] Kim YT, Minhas AS. Conductivity imaging of human lower extremity using MREIT with multi-echo pulse sequence and 3 ma imaging current: 2011 8th NFSI & ICBEM. Banff: IEEE, 2011: 48-52.

[23] Minhas AS, Meng ZJ, Kim YT, et al. Three-dimensional MREIT simulator (MREITSim): 2011 8th NFSI & ICBEM. Banff: IEEE, 2011: 64-67.

[24] Sadleir RJ, Sajib SZ, Kim HJ, et al. Simulations and phantom evaluations of magnetic resonance electrical impedance tomography (MREIT) for breast cancer detection. J Magn Reson, 2013, 230: 40-49.

[25] Sajib S, Kim HJ, Kim YT, et al. Potential of MREIT conductivity imaging to detect breast cancer: experimental and numerical simulation studies: 2012 Annual International Conference of the IEEE. San Diego: IEEE, 2012: 440-443.

[26] Yang L, Dai S. A simulation study on induced current magnetic resonance electrical impedance tomography of anisotropic brain tissues: 2010 3rd International Conference on Biomedical Engineering and Informatics (BMEI),Yantai, BMEI 2010: 75-77.

[27] 杨瑞霞. 磁共振电阻抗成像与乳腺癌早期检测. 山东轻工业学院学报(自然科学版), 2009, 23(1): 56-59.

[28] Kim YT, Meng Z, Minhas AS, et al. In vivo MREIT conductivity imaging of canine brain to evaluate ischemia and abscess, 2011: 44-47.

[29] Oh TI, Jeong WC, Mcewan A, et al. Feasibility of magnetic resonance electrical impedance tomography (MREIT) conductivity imaging to evaluate brain abscess lesion: in vivo canine model. J Magn Reson Imaging, 2013, 38(1): 189-197.

[30] 寿小婧, 魏青云, 赵莉娜, 等. 孤独症谱系障碍的功能磁共振成像研究进展. 中国医学影像学杂志, 2013, 21(8): 628-630, 633.

磁共振成像；电阻抗成像；综述

2014-05-15 【修回日期】2014-09-10

（本文编辑 张春辉）

R445.2

国家自然科学基金青年科学基金项目（NSFC-51107130）。

中国计量学院信息工程学院 浙江杭州 310018

闫丹丹 E-mail: dandanyan@cjlu.edu.cn

10.3969/j.issn.1005-5185.2014.09.020