单通道下基于盲源分离扩频通信抗干扰算法研究
沈 雷 盛 迪 孙闽红 王海泉 于 淼
(1.杭州电子科技大学通信工程学院,浙江 杭州310018;2.南京电讯技术研究所,江苏 南京210007)
引 言
扩频通信系统由于伪随机序列调制的保密性和发射的低功率特性,在军用通信、卫星导航等各个方面得到了广泛的应用.然而,现代通信系统往往会受到各种干扰源的干扰,使得通信系统性能降低.
为了提高扩频通信系统在干扰下的可靠性,必须采取一定的抗干扰措施.现有的干扰抑制技术有单通道的时域干扰预测抵消[1]、频域干扰抑制[2-4]和多通道的空域抗干扰[5-7]等方法.基于时域的干扰抵消技术利用干扰信号的相关性,通过时域滤波得到干扰信号的时域估计波形,并从接收到的信号中减去来消除干扰信号.基于变换域的处理技术主要利用扩频信号和白噪声的频谱相对比较平坦,而窄带干扰信号的频谱往往表现为很高很窄的冲激,从而可以在变换域中识别出存在干扰信号的谱线,通过相应的处理来去除干扰信号.这里的变换域滤波算法有基于快速傅里叶变换(Fast Fourier Transform,FFT)的频域干扰抑制方法[2],基于小波包变换的自适应干扰抑制方法[3],基于滤波器组的变换域干扰抑制技术[4].多通道的基于空域滤波的盲波束成形技术就是把时域滤波的原理推广到空域滤波[5],利用阵列天线技术使得天线波束方向对准扩频用户方向,波束零点对准干扰信号方向,从而降低干扰信号对扩频通信系统的影响.但是,多通道的空域滤波算法要求接收天线个数必须大于用户个数,并且其抗干扰性能也严重依赖于接收天线阵元个数.大规模天线阵元增加了接收机的成本、降低了终端的可移动性.而单通道的抗干扰算法仅利用一根接收天线来去除干扰信号,更适合移动终端.
目前的单通道抗干扰算法,主要包括基于时域和频域的滤波抗干扰算法.这些算法都是在某个域中对干扰信号进行估计的,然后从接收到的信号中减去估计的干扰信号.这种基于某个域的滤波算法,是从部分域对干扰信号进行估计和抵消的,因而其估计精度较低、抗干扰性能较差[8-9].
本文提出了单通道下基于扩频序列辅助的盲源分离扩频通信抗干扰方法.所提方法利用扩频序列的周期性,把多输入单输出(Multiple-Input Single-Output,MISO)信道建模成多输入多输出(MultipleInput Multiple-Output,MIMO)信道,从而把欠定盲源分离问题转换成超定盲源分离问题,克服了盲源分离对阵列天线个数的要求.所提的盲源分离方法,把干扰信号当作一种信源,利用扩频序列辅助的独立分量分析(Independent Component Analysis,ICA)算法对干扰信号和扩频信号进行分离.这种分离方法是从干扰信号和扩频信号的统计独立性出发的,是从信号整体特性对干扰信号进行估计分离来完成抗干扰的.从原理上讲,单通道下这种基于盲源分离的抗干扰方法性能比目前广泛应用的基于局部域估计的抗干扰方法(时域滤波抗干扰[8]、频域滤波抗干扰[9])具有更好的性能.理论分析和仿真结果表明了本文所提算法的有效性.
1 单通道盲源分离建模
本文研究的是存在多径的慢衰落信道,在接收到的M个信息序列时间内,信道衰落保持不变,此时接收到的基带信号可以表示为
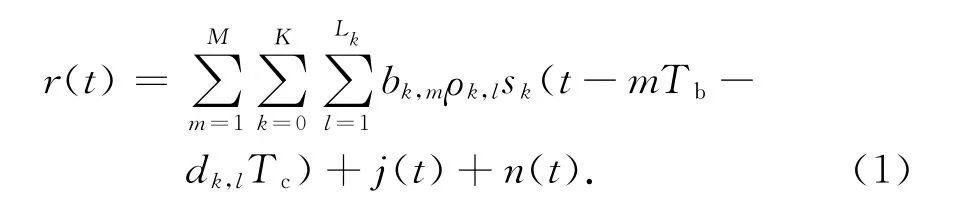
式中:b0,m、ρ0,l、d0,l和L0分别表示扩频用户的数据信息、第l个路径信号的幅度、以及以Tc为单位的离散量化的延迟和多径个数;s0(t)∈{±1}为扩频用户的扩频序列;bk,m、ρk,l、dk,l、Lk和sk(t)分 别 表 示第k个多址干扰信号的数据信息、多径信号的幅度、延迟、多径个数和扩频序列;Tb为信息比特持续时间,Tc为码片持续时间,且Tb=CTc,C为扩频序列的长度;M为观测信息比特数;n(t)为高斯噪声;这里假设j(t)=ρjcos(ωjt+θj)为单音干扰信号,ρj、ωj和θj分别为单音干扰信号的幅度、频率和相位.
由于在DS-CDMA的盲估计中每个码片持续时间Tc和扩频序列的长度C可以通过循环谱估计[10]和功率谱二次估计[11-12]等算法得到,因此本文中假设码片持续时间Tc和扩频序列的长度C为已知.对接收到的扩频信号r(t)以Tc进行采样,连续C个点组成如下向量为

定义一个长度为2C的向量qm:
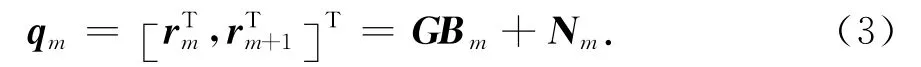
式中:Nm是方差为σ2的高斯噪声连续2C次采样得到的向量;混合矩阵G包含了扩频用户与干扰信号的特征序列[13]


G中包含的向量为

Bm是统计独立的信源组成的独立向量[13],包含了扩频用户和干扰信号的数据信息
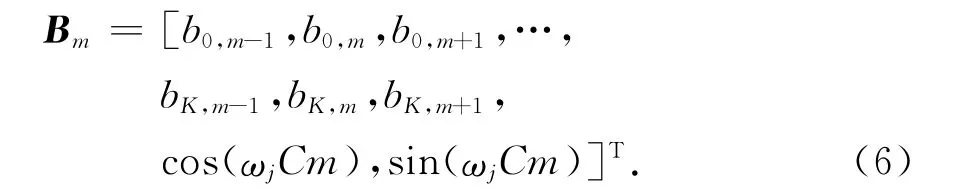
从式(4)~(6)可以得到,混合矩阵G的列向量包含了扩频用户、多址干扰和单音干扰信号的特征序列.其中扩频用户和多址干扰信号的特征序列是扩频序列,而单音干扰信号包含两个特征序列,分别为离散的正弦序列向量和余弦序列向量.信源向量Bm中包含了扩频用户和干扰信号的信息序列,其中单音干扰信号的信息序列是频率为ωjC的正弦波和余弦波.
2 基于扩频序列辅助的盲源分离抗干扰算法
由式(5)~(6)可知,混合矩阵G的列向量由扩频用户的扩频序列、多址干扰信号的扩频序列和单音干扰信号的正弦序列和余弦序列构成,则混和矩阵G是满秩的[13],并且信源矩阵中的各个信息序列满足统计独立性.本文所提算法,利用扩频序列的周期性,把单通道欠定盲源分离算法,建模成多输入多输出的超定盲源分离的形式.这种模型克服了传统的单通道盲源分离在欠定环境下没有稳定解的问题,并且可以采用ICA算法对扩频用户、多址干扰和单音干扰信号进行完全分离,从而完成抗干扰.
经典的ICA算法,存在多个局部收敛点[14].由于没有全局收敛点,分离顺序不确定,无法直接用来得到扩频用户的数据信息.本文提出的基于扩频序列辅助的ICA算法,利用扩频序列信息来构造正则函数对目标函数进行优化,使得目标函数具有全局最优解.利用ICA算法,迭代后收敛到唯一的最优解,分离出扩频用户的数据信息,完成抗干扰.
由于扩频信号是亚高斯信号,可选择四阶统计量峭度函数为目标函数.在扩频用户的扩频序列信息辅助下,寻找一个向量w,使得式(7)输出最大
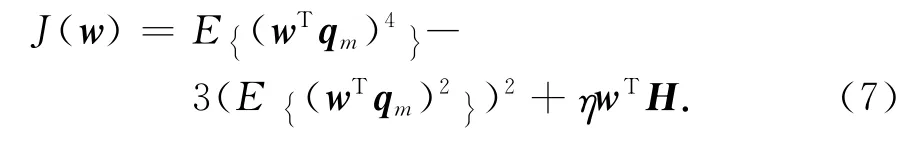
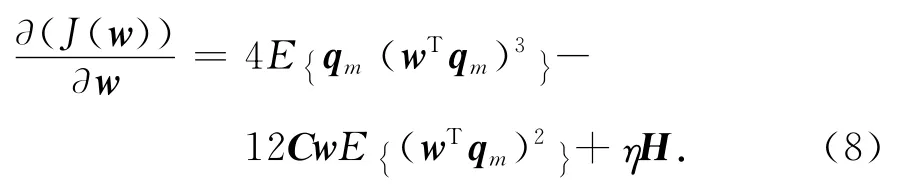

进而利用最陡下降法,可以得到迭代收敛公式为
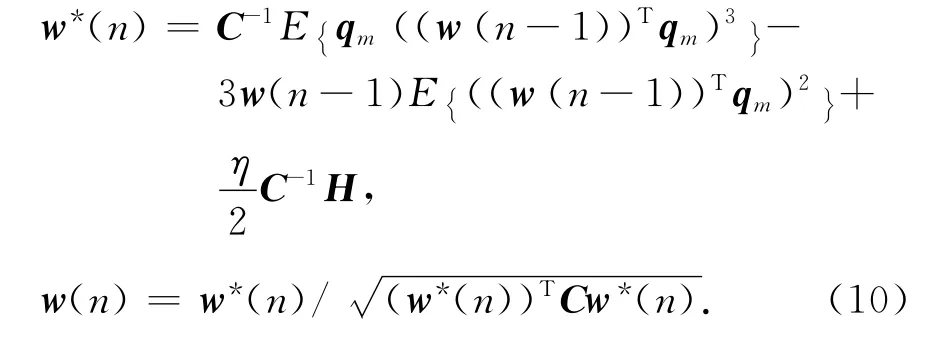
3 扩频序列辅助盲源分离抗干扰算法性能分析
由扩频序列辅助的盲源分离算法可以得到,盲源分离后的输出为

为了分析此盲源分离抗干扰算法的性能,下面采用均方误差MSE来衡量[15],其计算定义式为

为了求出上面定义的均方误差,需要求出wTopt的封闭表达式.由文献[15]结合式(9)可知,在高斯噪声下,在σ2=0处利用一个二阶泰勒级数对,其中表示σ4的无穷小量函数.是G2向量的伪逆向量,是噪声不存在时候的最优解.把的表达式代人式(11),可以得到

式中,β=Δw G2.由于盲源分离得到的输出信号的均方值为把式(13)代入可以得到然后把其再代入的表达式中,可以得到

把式(14)代人式(12)可以得到

式(15)为盲源分离抗干扰算法输出信号的均方误差MSE的表达式,其中右面第一项表示干扰信号对MSE估计的影响,其值与干信比成正比,与扩频序列的长度平方成反比,与干扰信号的特征序列的长度平方成正比.后两项与噪声方差σ2有关,且扩频序列的长度越长,滤波性能越好,信号估计均方误差越小.
4 仿真结果
为了验证所提抗干扰算法的性能,用Matlab对程序进行了仿真.仿真中扩频序列采用伪随机序列,长度为63.信息速率为1kHz,扩频后的码速率为63kHz,单音干扰信号载波频率采用4kHz.扩频用户和多址干扰信号的多径延迟为3个,幅度分别为1、0.5和0.2.用户和干扰信号的延迟在0和Tb之间等概率随机取值.慢衰落信道的持续时间为400个信息比特.为了比较,同时对目前常用的单通道下基于时域滤波[8]和频域滤波[9]的抗干扰算法性能也在相同环境下做了仿真.
在以下仿真中,正则化因子η取200.大量的仿真结果表明,此算法对η的依赖性不强,当η取值从4变化到100 000时算法依然能够取得同样好的性能.由此可知,η的可取范围多达5个数量级以上,说明此算法非常稳健.
图1给出了扩频通信中存在单音干扰信号,但不存在多址干扰信号环境下,单通道下三种抗干扰算法的误码率仿真曲线.横坐标为信噪比(RSN),在扩频序列长度63情况下,RSN=RSN,in+10lg63,纵坐标表示误码率(RBE),干信比(RJS)为25dB.由图1可以得到,在单音干扰信号下,所提的单通道下基于盲源分离的抗干扰算法比现在广泛应用的基于时域滤波和频域滤波的单通道抗干扰算法,性能有一定提高,并且逼近于无干扰时的误码率性能曲线.
图2给出了存在一个多址干扰和单音干扰信号时,三种抗干扰算法的误码率性能比较.横坐标为RSN,在扩频序列长度63情况下,RSN=RSN,in+10lg63,纵坐标表示RBE,多址干扰和单音干扰信号的RJS都为10dB.由图2可以看出,在宽带干扰和单音干扰信号都存在的环境下,所提的单通道下基于盲源分离的抗干扰算法比传统的基于时域滤波和频域滤波的单通道抗干扰算法具有更好的性能,而且这种性能的提高比只有单音干扰信号时候的效果更明显.这是由于时域滤波和频域滤波抗干扰对多址干扰信号消除性能下降,而所提的方法对多址干扰信号依旧具有良好的抗干扰效果.

图1 RJS=25dB单音干扰下抗干扰算法RBE性能比较

图2 RJS=10dB多址干扰和单音干扰下抗干扰算法RBE性能比较
图3给出了单音干扰信号下,三种抗干扰算法估计得到的扩频信号幅度的估计精度.横坐标为RSN,在扩频 序列长度63情况下,RSN=RSN,in+10lg63,纵坐标表示均方误差MSE,RJS为25dB.由图3可见,所提的单通道下基于盲源分离的抗干扰算法性能最佳,明显优于传统的基于时域滤波和频域滤波的单通道抗干扰算法性能.图3中,盲源分离RMS计算值是公式(15)的计算值,这个值与盲源分离MSE仿真值吻合,验证了式(15)的正确性.

图3 RJS=25dB单音干扰下抗干扰算法MSE性能比较
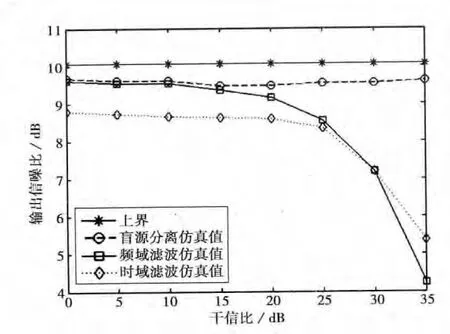
图4 单音干扰下RSN,out与RJS的关系曲线
图4给出了单音干扰信号下,三种抗干扰算法的相关输出信噪比与干信比的关系曲线.横坐标为RJS,纵坐标表示输出信噪比RSN,out,输入信噪比RSN,in为-8dB.由图4看出,所提的单通道下基于盲源分离的抗干扰算法对干信比不敏感,输出信噪比不会随着干信比的增加而下降,并且高于传统的基于时域滤波和频域滤波的单通道抗干扰算法的,接近于理论上限.而传统的基于时域滤波和频域滤波的抗干扰算法,随着干信比的增大到某个门限,抗干扰性能快速下降.表明所提的抗干扰算法在单音干扰信号下比传统的基于时域滤波和频域滤波的抗干扰算法具有更好的性能.
5 结 论
论文提出了单通道下基于盲源分离的抗干扰方法.该方法利用扩频序列的周期性,把单通道下接收到的信号,建模成多输入多输出的盲源分离模型.论文所提方法利用扩频序列信息对基于峭度的目标函数进行正则化,使得目标函数具有全局收敛点,克服了独立分量分析算法分离顺序不确定的缺点.所提方法在进行抗干扰时完成解扩,同时得到期望扩频用户的数据信息.所提方法从整体域统计特性出发,对干扰信号进行估计分离来完成抗干扰.理论分析和仿真结果表明了这种基于整体域统计特性的盲源分离抗干扰方法比传统的基于局部域滤波的抗干扰方法具有更好的性能.
[1]AMIN M G,WANG C,LINDSEY A R.Optimum interference excision in spread spectrum communications using open-loop adaptive filters[J].Signal Processing,IEEE Transactions on,1999,47(7):1966-1976.
[2]ANDO S,NARA T.An exact direct method of sinusoidal parameter estimation derived from finite Fourier integral of differential equation[J].Signal Processing,IEEE Transactions on,2009,57(9):3317-3329.
[3]JIANG Y,GAO H Y,YU S P.Adaptive interference excision in digital spread spectrum communication systems based on wavelet packet transform[C]//Machine Learning and Cybernetics,2007International Conference on.IEEE,2007,6:3278-3282.
[4]STITZ T H,RENFORS M.Filter-bank-based narrowband interference detection and suppression in spread spectrum systems[J].EURASIP Journal on Applied Signal Processing,2004,2004(8):1163-1176.
[5]YU K B,MURROW D J.Adaptive digital beamforming for angle estimation in jamming[J].IEEE Transactions on Aerospace and Electronic Systems,2001,37(2):508-523.
[6]WANG N,AGATHOKLIS P,ANTONIOU A.A new DOA estimation technique based on subarray beamforming[J].IEEE Transactions on Signal Processing,2006,54(9):3279-3290.
[7]刘聪锋,廖桂生.基于空域滤波的方向波数域测向测频新方法[J].电波科学学报,2010,25(1):60-65.LIU Congfeng,LIAO Guisheng.Novel method of angle and frequency estimation in direction wavenumber region using space filtering[J].Chinese Journal of Radio Science,2010,25(1):60-65.(in Chinese)
[8]WU W R,YU F F.New nonlinear algorithms for estimating and suppressing narrowband interference in DS spread spectrum systems[J].Communications,IEEE Transactions on,1996,44(4):508-515.
[9]刘拥军,胡捍英.GPS频域抗干扰算法研究[J].信号处理,2009,25(11):1738-1741.LIU Yongjun,HU Hanying.The study of GPS frequency domain anti-jamming algorithms[J].Signal Processing,2009,25(11):1738-1741.(in Chinese)
[10]MAZET L,LOUBATON P.Cyclic correlation based symbol rate estimation[C]//Thirty-Third Asilomar Conference on IEEE Signals Systems,and Computers,1999,2:1008-1012.
[11]张天骐,周正中.直扩信号伪码周期的谱检测[J].电波科学学报,2001,16(4):518-521.ZHANG Tianqi,ZHOU Zhengzhong.A new spectral method of periodic detection of PN sequences in lower SNR DS/SS signals[J].Chinese Journal of Radio Science,2001,16(4):518-521.(in Chinese)
[12]张天骐,林孝康,周正中.一种直扩信号伪码周期及序列的盲估计方法[J].电波科学学报,2005,20(3):400-405.ZHANG Tianqi,LIN Xiaokang,ZHOU Zhengzhong.A new method for periodic and sequence estimation of the PN code in the lower SNR DS/SS signals[J].Chinese Journal of Radio Science,2005,20(3):400-405.(in Chinese)
[13]HYVARINEN A,OJA E.Independent component analysis:algorithms and application[J].Neural Networks,2000,13(4):411-430.
[14]EKICI O,YONGACOLU A.Application of noisy-independent component analysis for CDMA signal separation[C]//2004IEEE 60th Vehicular Technology Conference,2004.VTC2004-Fall,2004,5:3812-3816.
[15]LOESCH B,YANG B.On the relation between ICA and MMSE based source separation[C]//2011IEEE International conference on Acoustics,Speech and Signal Processing(ICASSP),2011:3720-3723.

