高斯型功率谱噪声调频信号的性能分析

翁晓明 史小斌 顾 红 苏卫民

（南京理工大学 电子工程与光电技术学院，江苏 南京210094）

引 言

随机噪声雷达是以随机噪声信号为发射信号的一类雷达.由于随机噪声信号的无规律性，随机噪声雷达会有一些不同于常规雷达的特性，包括强电子反对抗能力（Electronic Counter Countermeasure，ECCM）、低截获概率（Low Probability of Intercept，LPI）、低识别概率（Low Probability of Detecting，LPD）等［1-3］.随机噪声信号具有“图钉型”的模糊函数，因此不存在测距测速模糊［4-5］，同时由于随机噪声信号在频域同样具有随机性，相同频段的随机噪声雷达间的相互干扰很小，使得随机噪声雷达具有较高的频谱利用率［6］.随机噪声雷达理论产生于20世纪50年代［7-8］，并于近些年应用于近距离成像，穿墙成像等领域［9-11］，得到了较为广泛的关注与发展.

如今，随机噪声雷达已由原先的直接发射非调制噪声信号转向发射通过噪声调频得到的信号［12］，其好处在于：噪声调频（Noise Frequency Modulation，NFM）信号的功率仅与载波功率有关，具有较低的峰均功率比（Peak to Average Power Ratio，PAPR）［13］；NFM信号在一定条件下具有高斯型的功率谱，从而具有单瓣的高斯型自相关函数，具有较高的峰值旁瓣比（Peak Side-Lobe Ratio，PSLR）［12，14］.但是高斯型 的功率谱存在一个问题，其理论上无穷的宽度与实际工程中有限的系统带宽形成矛盾.在实际工程中，更多关心的是NFM信号所需的最低系统带宽以及在此带宽下的信号能量与距离分辨力.文献［14-15］计算并给出了NFM信号的半功率带宽（Half Power Bandwidth，HPB）以及均方根带宽（Root Mean Square Bandwidth，RMSB）表达式，由于高斯型功率谱与传统矩形功率谱相比，形状上差别较大，两种带宽均不能表示NFM信号所需要的最低系统带宽.文献［16-17］推导了NFM信号的能量及距离分辨力表达式，但均未考虑系统带限对于理论宽度无穷的高斯型功率谱的作用，以及由此带来的对信号能量及距离分辨力的影响.

本文推导了在系统带限的情况下，具有高斯型功率谱的NFM信号的能量与距离分辨力的精确数学表达式，指出了在不过度损失信号能量及距离分辨力的条件下NFM信号所需的最低系统带宽，通过仿真实验验证了推导结果的正确性.

1 噪声调频信号

NFM信号的时域复数形式表达式为

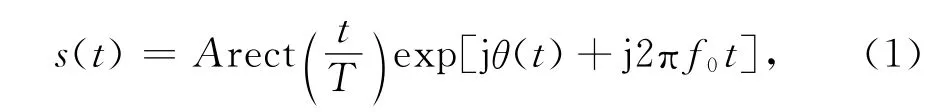
式中：A为幅度；T为脉宽；f0为载频；rect（x）＝1，x≤｜0.5｜为矩形函数；信号相位θ（t）＝2πKfm为调制斜率，调制噪声u（x）为广义平稳窄带高斯白噪声，其功率谱密度表达式为

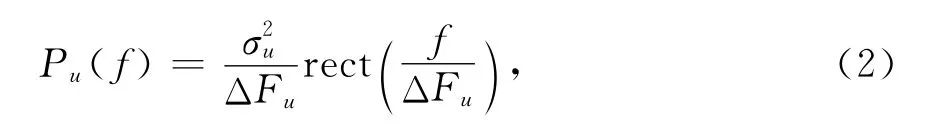
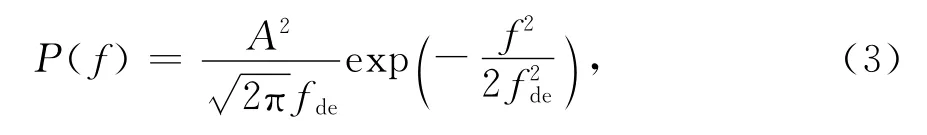
式中fde＝Kfmσu为有效调制带宽.由式（3）可以得到XdB带宽与有效调制带宽之间的关系为

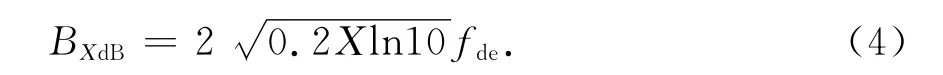
图1给出了有效调制带宽fde＝15MHz时仿真与理论的NFM信号功率谱密度.由式（4），此参数下NFM信号的3dB带宽（X＝3时）约为35 MHz，由于高斯函数具有较长拖尾，图1中功率谱在频率轴上占据的范围远大于35MHz，显然工程中关心的NFM信号所需的系统带宽无法用3dB带宽准确衡量.此参数下NFM信号的20dB带宽（X＝20时）约为90MHz.从图1中可以看到，超过±45MHz时信号功率谱幅度已经低于-20dB，因此近似认为NFM信号的最大调制带宽为其20dB带宽.

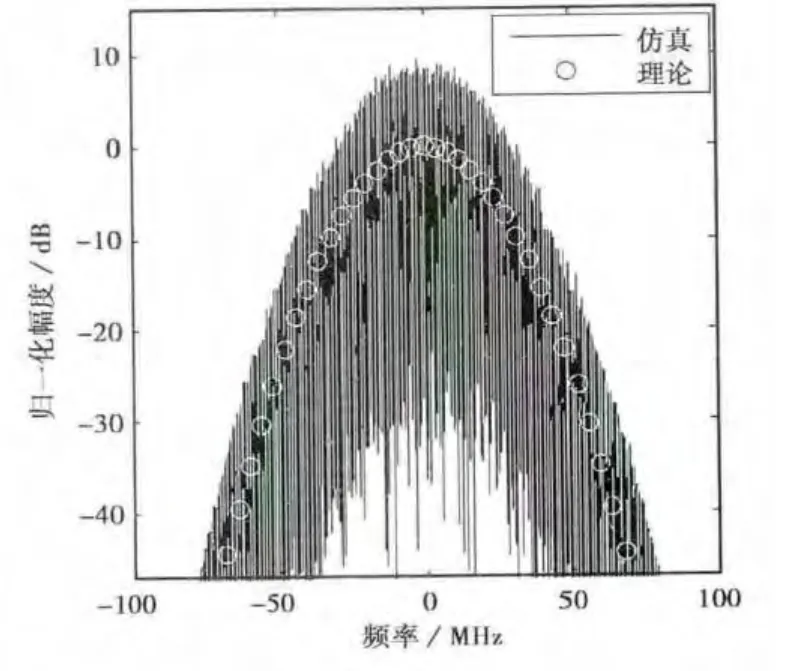
图1 NFM信号在fde＝15MHz时理论与仿真的功率谱密度

2 信号能量

由式（1），幅度为A、脉宽为T的NFM信号总能量为［16］

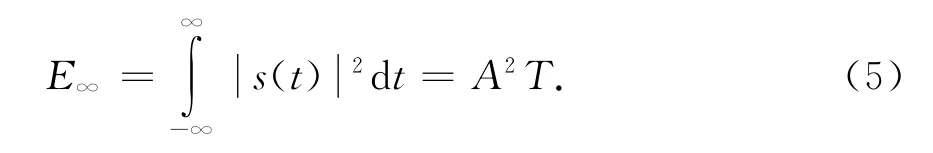
实际信号处理系统带宽必然有限，为了避免混叠，信号需要通过抗混叠滤波器强制带限至系统带宽.理想的抗混叠滤波器的频率响应为

式中Ωc为滤波器带宽.由于高斯型功率谱具有无穷的宽度，通过抗混叠滤波器后，NFM信号能量会有一定的损失.由式（3）及式（6），通过抗混叠滤波器后，幅度为A、脉宽为T的NFM信号能量为

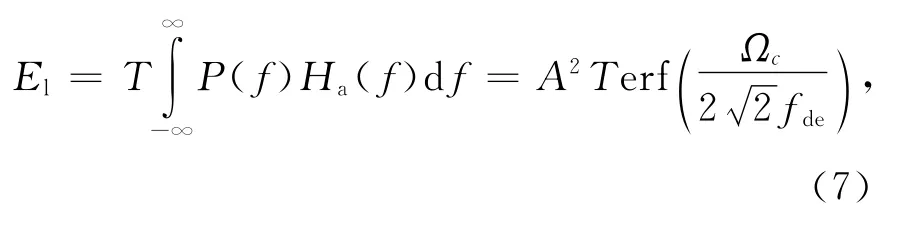
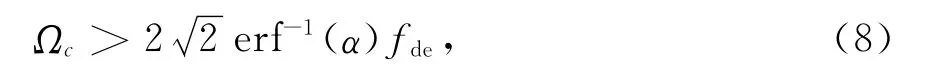
式中erf-1（·）表示误差函数的反函数.举例来说，若希望因带限造成的NFM信号能量损失小于其总能量的5%，即α＞0.95，由式（8）得到Ωc＞3.92 fde，又由式（4）得到3.92fde≈9dB带宽.综上可知，能量损失小于5%所需的抗混叠滤波器带宽或者说系统带宽应至少大于NFM信号的9dB带宽.

3 距离分辨力

根据Wiener-Khinchine定理，NFM信号的自相关函数为其功率谱的傅里叶逆变换，即由式（3）的傅里叶逆变换得到

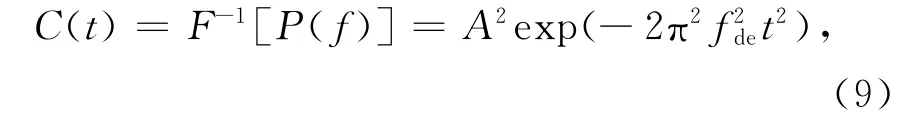
式中F-1（·）表示对于频率f的傅里叶逆变换.图2给出了有效调制带宽为15MHz时NFM信号仿真与理论的自相关函数.由图2，NFM信号的自相关函数仅具有单一主瓣，旁瓣表现为均匀噪声基底且幅度较低［12，18］，因此，其自相关函数的-3dB主瓣宽度可以较准确地衡量其距离分辨力.令C（tρ）代入式（9），得到时间量纲下NFM信号自相关函数-3dB主瓣宽度，即距离分辨力为

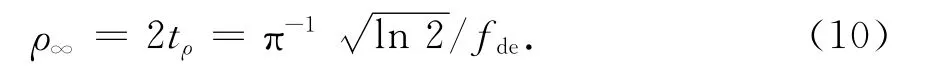
系统带限时，由于抗混叠滤波器对于高斯型功率谱形状的修正，自相关函数主瓣存在一定程度的展宽，距离分辨力会有所下降.考虑由式（6）表示的抗混叠滤波器的影响，式（9）修正为

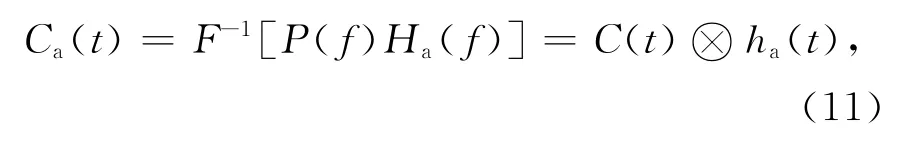
式中⊗为卷积符号，且有

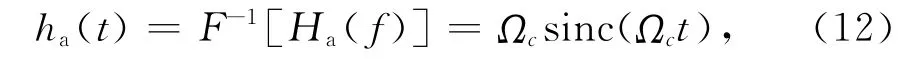
式中sinc（x）＝sin（πx）／（πx）.式（11）中sinc函数与高斯函数的卷积无法计算得到解析表达式，需要对式（12）做近似处理.根据Taylor展开，在x＝0点附近可以近似认为sinc（x）≈exp（-π2x2／6），同时考虑到当Ωc与fde相近时，Ha（f）在边缘处应具有陡峭的衰减，体现出其带限作用；当Ωc≫fde时，Ha（f）应近似为一矩形函数，具有较为平坦的幅频响应.综上，对ha（t）作如下近似：当Ωc／fde＜6时，ha（t）的近似高斯函数表达式为

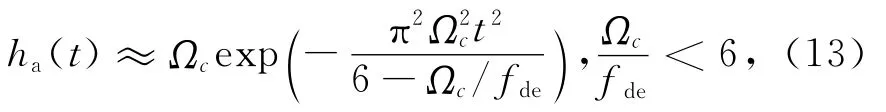
当Ωc／fde≥6时，ha（t）主峰宽度要比C（t）窄得多，近似认为ha（t）＝δ（t）为一个冲激函数.则式（11）可以改写成

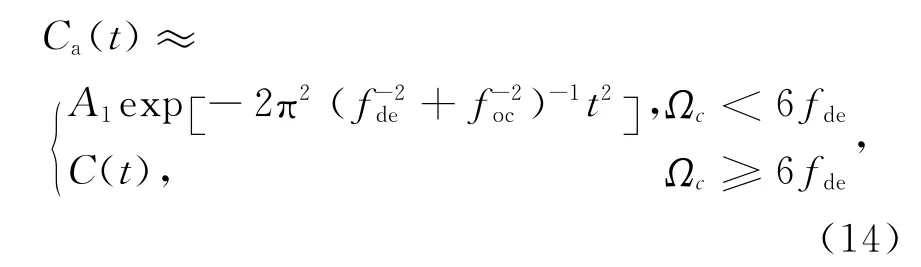
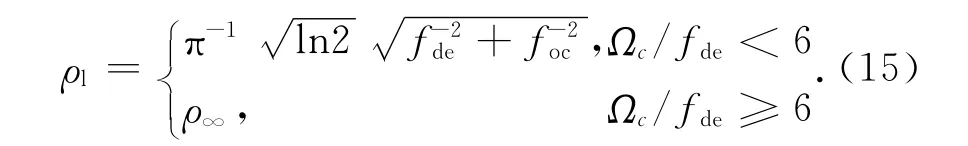
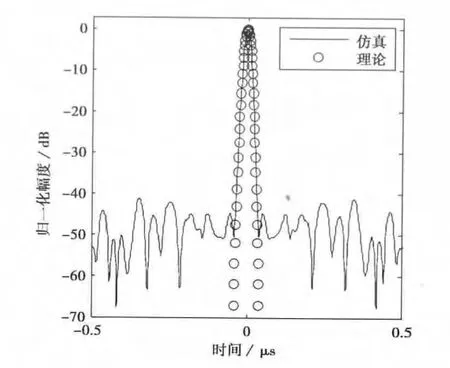
图2 NFM信号在fde＝15MHz时理论与仿真的自相关函数

由式（15）可知，当Ωc／fde＜6时，NFM信号自相关函数主瓣宽度因为多了一项foc而有所展宽；当Ωc／fde≥6时，近似认为系统带限对NFM信号没有影响，其自相关函数主瓣宽度没有变化.此处同样以Ωc等于9dB带宽为例，由前文所述可知此时Ωc≈4fde，代回式（15），得到.即由于带限的影响，NFM信号的自相关函数-3dB主瓣展宽了约倍.由于主瓣展宽程度随着foc的增大而减小，可知展宽不超过原宽度的1.12倍所需的抗混叠滤波器带宽，或者说系统带宽应至少大于NFM信号的9dB带宽.

4 仿真实验

以下通过仿真实验验证前文结论的正确性.仿真信号为具有高斯型功率谱的NFM信号，仿真参数：信号脉宽为50μs，有效调制带宽（fde）为15 MHz，抗混叠滤波器带宽（Ωc）从NFM信号的1dB带宽（约20.4MHz）变化至25dB带宽（约101.8MHz）.

图3给出了在不同抗混叠滤波器带宽（Ωc）时，NFM信号能量的理论与仿真曲线.图3纵坐标为滤波后与滤波前NFM信号能量之比，横坐标为抗混叠滤波器带宽Ωc（换算为XdB带宽）.仿真曲线与理论曲线吻合.由图3可知，Ωc／fde越大，El／E∞越大，能量的损失越小.当Ωc＞9dB带宽时，El／E∞＞0.958，此时带限造成的能量损失小于信号总能量的5%.当Ωc＞20dB带宽时，El／E∞＞0.99，几乎不存在能量损失，与式（7）的结论相吻合.

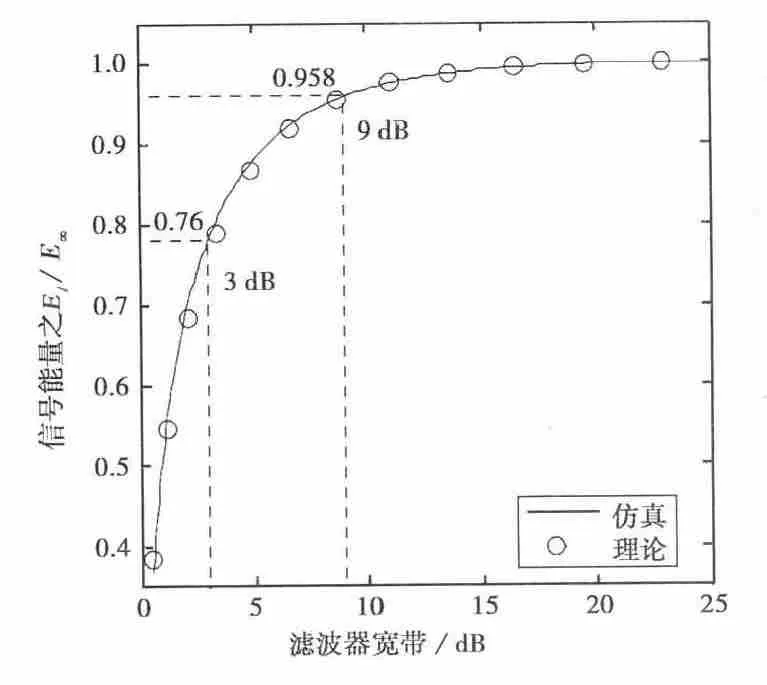
图3 NFM信号在不同Ωc时理论与仿真的能量

图4给出了在不同抗混叠滤波器带宽（Ωc）时，NFM信号自相关函数-3dB主瓣宽度，即信号距离分辨力的理论与仿真曲线.图4纵坐标为滤波后与滤波前NFM信号自相关函数-3dB主瓣宽度之比，横坐标为抗混叠滤波器带宽Ωc（换算为XdB带宽）.仿真曲线与理论曲线吻合，图4中误差主要来自式（13）的近似处理.由图4可知，Ωc／fde越大，ρl／ρ∞越小，主瓣展宽程度越小.同样可以看到，当Ωc＝9dB带宽时，ρl／ρ∞＝1.118，即主瓣展宽为原宽度的1.118倍.当Ωc＞20dB带宽时，ρl／ρ∞≈1，其主瓣宽度几乎没有任何展宽，与式（15）的结论相吻合.

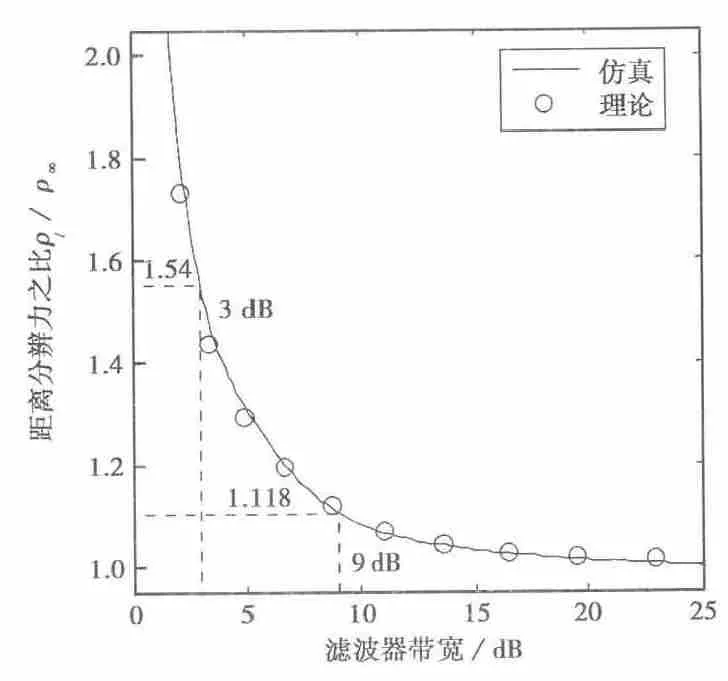
图4 NFM信号在不同Ωc时理论与仿真的距离分辨力

由图3以及图4还可知，若信号处理系统带宽以NFM信号的3dB带宽（半功率带宽，约等于2.35倍有效调制带宽）为设计依据，能量损失超过信号总能量的23%，主瓣展宽超过原宽度的1.5倍，显然与设计初衷不符，故3dB带宽明显小于NFM信号所需的最低系统带宽.当系统带宽不低于NFM信号的9dB带宽（约等于4倍有效调制带宽）时，信号能量损失不超过5%，主瓣展宽不超过12%，可近似认为9dB带宽为NFM信号所需的最低系统带宽.当系统带宽不低于NFM信号的20dB带宽（最大调制带宽，约等于6倍有效调制带宽）时，信号能量以及主瓣展宽程度均小于1%，几乎可以忽略不计，但与系统带宽限定于9dB带宽相比，所需的系统带宽提高了50%，而信号能量及距离分辨力的提高并不明显，说明最大调制带宽作为NFM信号的系统带宽过宽，实际对系统资源造成了一定的浪费.

5 结 论

本文推导了在带限情况下，具有高斯型功率谱的NFM信号能量与距离分辨力的数学表达式，并指出NFM信号所需的系统带宽应大于等于其9dB带宽以使得信号能量与距离分辨力均不会因带限而产生较大损失，同时应小于等于其20dB带宽以避免对于系统资源的浪费.实际工程中，也可根据需求，直接利用式（7）及式（15）推算出NFM信号能量、距离分辨力与所需系统带宽等参数，为NFM信号的波形设计提供理论依据.

［1］GARMATYUK D S，NARAYANAN R M.ECCM capabilities of an ultrawideband bandlimited random noise imaging radar［J］.IEEE Transactions on Aerospace and Electronic Systems，2002，38（4）：1243-1255.

［2］THAYAPARAN T，DAKOVIC M，STANKOVIC L.Mutual interference and low probability of interception capabilities of noise radar［J］.IET Radar，Sonar and Navigation，2008，2（4）：294-305.

［3］张新相，吴铁平，陈天麒.随机噪声雷达抗干扰性能分析［J］.电波科学学报，2008，23（1）：189-194.ZHANG Xinxiang，WU Tieping，CHEN Tianqi.ECCM capabilities of random signal radar［J］.Chinese Journal of Radio Science，2008，23（1）：189-194.（in Chinese）

［4］LIU Guosui，GU Hong，SU Weimin，et al.Random signal radar-a winner in both the military and civilian operating environments［J］.IEEE Transactions on Aerospace and Electronic Systems，2003，39（2）：489-498.

［5］GOVONI M A，LI H B，KOSINSKI J A.Rangedoppler resolution of the linear-FM noise radar waveform［J］.IEEE Transactions on Aerospace and Electronic Systems，2013，49（1）：658-664.

［6］KULPA K，GAJO Z，MALANOWSKI M.Robustification of noise radar［J］.IET Radar，Sonar and Navigation，2008，2（4）：284-293.

［7］HORTON B M.Noise-modulated distance measuring system［J］.Proc Institute of Radio Engineers（IRE）.1959，47（5）：821-828.

［8］LUKIN K A，NARAYANAN R M.Fifty years of noise radar［C］／／11th International Radar Symposium（IRS）.Vilnius，Lithuania，2010：504-506.

［9］TARCHI D，LUKIN K A，FORTUNY G J.SAR imaging with noise radar［J］.IEEE Transactions on Aerospace and Electronic Systems，2010，46（3）：1214-1225.

［10］CHEN P H，SHASTRY M C，LAI C P，et al.A portable real time digital noise radar system for through-the-wall imaging［J］.IEEE Transactions on Geoscience and Remote Sensing，2012，50（10）：4123-4134.

［11］MALANOWSKI M，KULPA K.Detection of moving targets with continuous-wave noise radar：theory and measurements［J］.IEEE Transactions on Geoscience and Remote Sensing，2012，50（9）：3502-3509.

［12］AXELSSON S R J.Noise radar using random phase and frequency modulation［J］.IEEE Transactions on Geoscience and Remote Sensing，2004，42（11）：2370-2384.

［13］高许岗.随机噪声合成孔径雷达性能分析及其信号处理技术研究［D］.南京：南京理工大学，2011.GAO Xugang.Research on performance of random noise SAR and its signal processing technique［D］.Nanjing：Nanjing University of Science ＆Technology of China，2011.（in Chinese）

［14］张先义，苏卫民，顾 红.随机噪声超宽带雷达信号性能分析［J］.兵工学报，2007，28（5）：557-560.ZHANG Xianyi，SU Weimin，GU Hong.Performance analysis for random noise ultra-wideband radar signal［J］.Acta Armamentarii，2007，28（5）：557-560.（in Chinese）

［15］武 昕，李 澍，刘 畅，等.基于特征参数的随机噪声雷达相关输出研究［J］.电波科学学报，2012，27（3）：543-550.WU Xin，LI Shu，LIU Chang，et al.Correlation output of noise radar based on characteristic parameters［J］.Chinese Journal of Radio Science，2012，27（3）：543-550.（in Chinese）

［16］高许岗，苏卫民，顾 红，等.随机噪声雷达信号性能分析［J］.南京理工大学学报：自然科学版，2010，34（1）：126-130.GAO Xugang，SU Weimin，GU Hong，et al.Performance analysis of random noise radar signal［J］.Journal of Nanjing University of Science ＆Technology Natural Science，2010，34（1）：126-130.（in Chinese）

［17］高许岗，苏卫民，顾 红.随机噪声连续波SAR的性能分析［J］.电波科学学报，2010，25（1）：47-51.GAO Xugang，SU Weimin，GU Hong.Performance analysis of random noise CW SAR［J］.Chinese Journal of Radio Science，2010，25（1）：47-51.（in Chinese）

［18］程院兵，张 卫，顾 红，等.噪声连续波雷达脉压输出主旁瓣比推导与分析［J］.兵工学报，2012，33（1）：1-6.CHENG Yuanbing，ZHANG Wei，GU Hong，et al.Derivation and analysis of mainlobe to sidelobe ratio after pulse compression in noise continuous wave radar［J］.Acta Armamentarii，2012，33（1）：1-6.（in Chinese）