加肋锥－环－柱结合壳应力峰值的计算方法

吕岩松

(海军工程大学，湖北 武汉 430033）

加肋锥－环－柱结合壳应力峰值的计算方法

吕岩松

(海军工程大学，湖北 武汉 430033）

提出加肋锥－环－柱结合壳环壳块应力峰值的计算公式，并通过数值计算，拟合出公式中参数的计算曲线，为潜艇加肋锥－环－柱结合壳结构的初步设计提供方便快捷的计算方法。公式的计算结果与分区样条等参元方法的计算结果相对误差较小，可以在工程中应用。

加肋锥－环－柱结合壳;环壳块;应力峰值;计算方法

0 引言

在现代潜艇耐压艇体结构设计中，通常采用锥壳将不同直径的圆柱壳连接起来，形成锥－柱结合壳。在锥、柱结合部由于壳体子午线切线倾角不连续，会产生很大的局部弯曲应力，应力集中十分明显。黄加强和郭日修［1］等提出在锥－柱结合部嵌入一段环壳块，即采用加肋锥－环－柱结合壳来降低结合部的应力集中，以分区样条等参元方法计算加肋锥－环－柱结合壳的应力和稳定性［2］，并进行了一系列的精车模型试验和焊接模型试验［3－4］(见图1）。模型试验结果表明，以分区样条等参元方法计算加肋锥－环－柱结合壳的应力分布，计算结果与试验结果吻合良好。

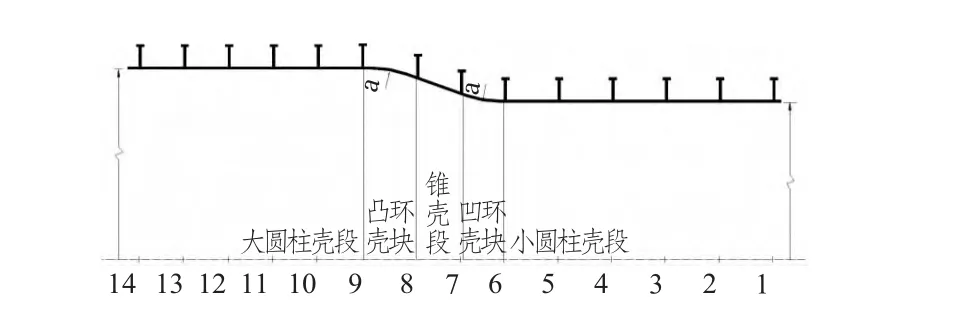
图1 加肋锥－环－柱结合壳Fig.1 Ring-stiffened cone-toroid-cylinder combination shell

在对潜艇加肋锥－环－柱结合壳进行结构设计时，以分区样条等参元方法进行强度计算，需要首先建立有限元模型。如果能够提出加肋锥－环－柱结合壳环壳块应力峰值的计算公式，则可以大大简化计算过程。文献 ［5］利用内力和位移的连续条件，以解析法计算锥－环－柱结合壳环壳块的应力。文献 ［6］将锥－环－柱结合壳简化为无限长的弹性基础梁，提出用显式表示的环壳块的应力计算公式。但上述方法均未计入肋骨对组合壳应力分布的影响，由于潜艇耐压壳体为加肋组合壳，因此需要考虑肋骨的影响。

本文提出计算加肋锥－环－柱结合壳环壳块应力峰值的显式公式，利用分区样条等参元方法，对大量的计算模型进行数值分析，拟合出公式中参数的计算曲线。该显式公式在潜艇加肋锥－环－柱结合壳初步设计时使用，可以方便地得到加肋锥－环－柱结合壳环壳块的应力峰值。

1 加肋锥－环－柱结合壳环壳块应力峰值计算公式

文献［6］利用无限长弹性基础梁的计算方法近似计算锥－环－柱结合壳的应力，提出下列公式:

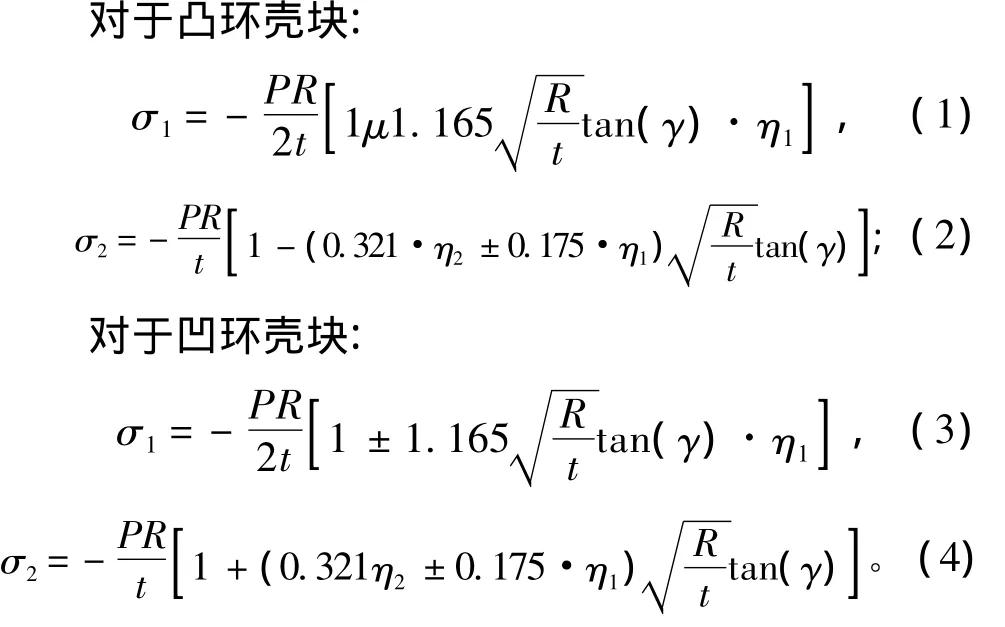
式中:a为环壳块半径;R为与环壳块相邻的圆柱壳半径;γ为锥壳半锥角;t为环壳块厚度。

并给出η1和η2的计算曲线。借鉴该公式的形式，并考虑到实际工程应用时，对于凸环壳块，应校核其中部最大内表面纵向应力;对于凹环壳块，应校核其中部最大中面环向应力，因此本文提出加肋锥－环－柱结合壳环壳块应力峰值的计算公式:

式中k1和k2为计算参数，需通过数值计算拟合得到。

2 系数k1和k2的计算

参照潜艇的结构参数，建立252个计算模型，以

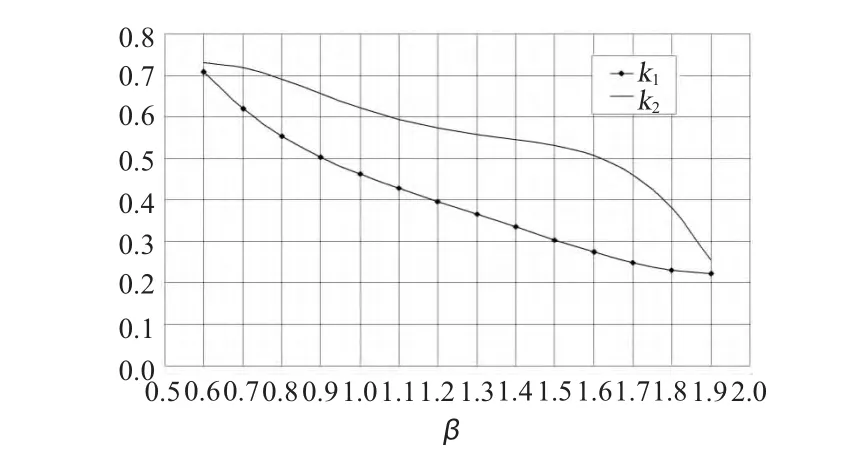
图2 k1和k2计算曲线Fig.2 Calculation curve of k1 and k2

利用式(5）、式(6）和图2，可以快速得到加肋锥－环－柱结合壳凸环壳块和凹环壳块的应力峰值。在潜艇加肋锥－环－柱结合壳的初步设计阶段，可以省略建立有限元模型的繁杂过程。

3 误差分析

为分析本文提出公式的计算误差，分别以本文公式和分区样条等参元方法对某加肋锥－环－柱结合壳进行应力计算，表1和表2给出了计算结果。

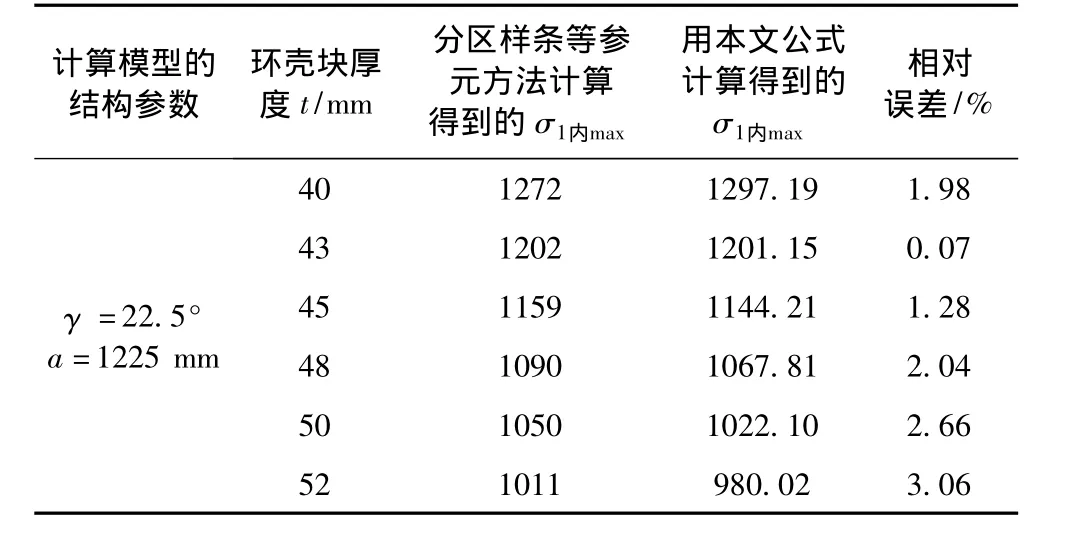
表1 凸环壳块应力计算结果 单位:MPaTab.1 Stress at convex toroid segment(MPa）

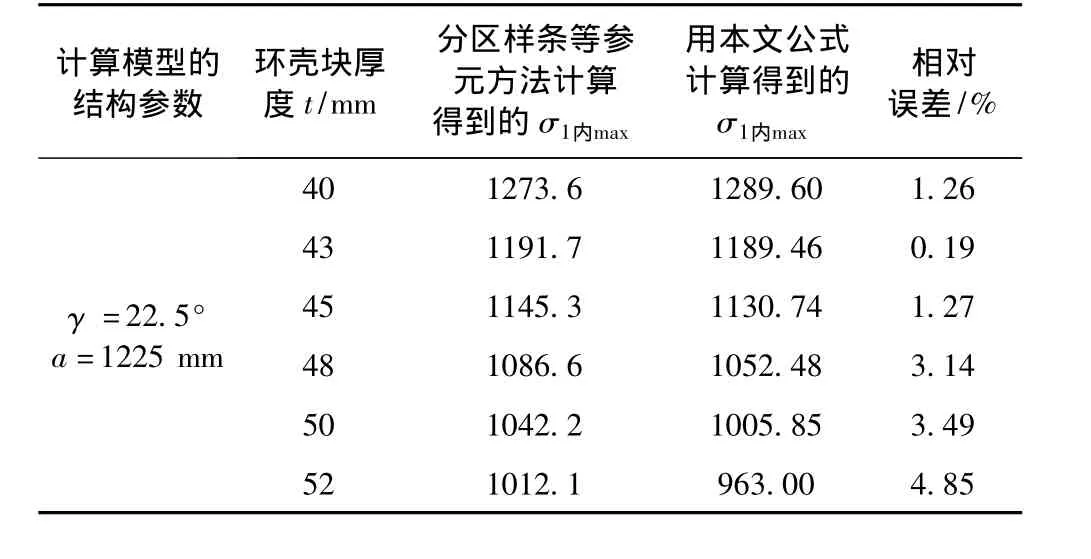
表2 凹环壳块应力计算结果 单位:MPaTab.2 Stress at concave toroid segment(MPa）

由表1和表2可以看出，本文方法与分区样条等参元方法计算结果的相对误差在5%以内，能够满足工程使用的要求。

4 结语

本文提出潜艇加肋锥－环－柱结合壳环壳块应力峰值的计算公式，在加肋锥－环－柱结合壳的初步设计阶段，利用该公式可以方便快捷地得到凸环壳块和凹环壳块的应力峰值，从而省略了建立有限元模型的繁杂过程。本文方法与分区样条等参元方法计算结果的相对误差较小，可以在工程中应用。

［1］黄加强，郭日修.加肋锥－环－柱组合壳强度及稳定性模型实验研究［J］.中国造船，1998(4）:57－65.

HUANG Jia-qiang，GUO Ri-xiu.Model experimental research on stresses and stability of ring-stiffened conetoroid-cylinder combined shell［J］.Shipbuilding of China，1998(4）:57－65.

［2］黄加强，郭日修.分区样条等参元方法分析加肋轴对称组合壳［J］.计算力学学报，1998，15(1）:58 －68.

HUANG Jia-qiang，GUO Ri-xiu.Sub region isoparametric spline element analysis of strength and stability of ring stiffened combined shell of revolution［J］.Chinese Journal of Computational Mechanics，1998，15(1）:58 －68.

［3］郭日修，吕岩松，黄加强，等.加肋锥－环－柱结合壳试验研究［J］.船舶力学，2008，12(2）:252 －257.

GUO Ri-xiu，LV Yan-song，HUANG Jia-qiang，et al.Experimental research on the ring-stiffened cone-toroidcylinder combination shell［J］.Journal of Ship Mechanics，2008，12(2）:252 －257.

［4］白雪飞，陈昕，丁锦超，等.凹型加肋锥－环－柱结合壳强度的模型试验研究［J］.船舶力学，2006，10(2）:65 －72.

BAI Xue-fei， CHEN Xin， DING Jin-chao， et al.Experimental research of the strength of ring-stiffened concave cone-toroid-cylinder combined shell［J］.Journal of Ship Mechanics，2006，10(2）:65 －72.

［5］王安稳.有环壳过渡段的锥－柱组合壳的应力和稳定性［J］.应用力学学报，1997，14(1）:128 －135.

WANG An-wen.Stress and stability of cone cylinder with toroidal transition［J］.Chinese Journal Applied Mechanics，1997，14(1）:128 －135.

［6］戴自昶.锥－环－柱结合壳和锥－柱结合壳应力的近似解［J］.舰船科学技术，2002，24(5）:3－27.

DAI Zi-chang.Approximate solutions of stress in conetoroid-cylinder and cone-cylinder complex shell［J］.Ship Science and Technology，2002，24(5）:3－27.

Calculation of peak stress of ring-stiffened cone-toroid-cylinder combination shell

LV Yan-song
(Naval University of Engineering，Wuhan 430033，China）

A formula which could be used to calculate the peak stress of ring－stiffened cone-toroidcylinder combination shell is presented in this paper.The parameters in formula are presented by numerical calculation.By formula in this paper，it is easy to calculate the peak stress of ring-stiffened cone-toroidcylinder combination shell.The results of formula are good agreement with the results of sub region isoparametric spline elementmethod and the formula could be used in engineering.

ring-stiffened cone-toroid-cylinder combination shell;toroid segment;peak stress;calculation method

U663.1

A

1672－7649(2014）04－0063－03

10.3404/j.issn.1672－7649.2014.04.012

2012－11－20;

2012－12－31

吕岩松(1976－），男，博士，讲师，主要从事船舶结构力学和潜艇强度研究。