舰船水下爆炸冲击环境实用建模方法

孙 丰，吴 彬，王 喆，白兆宏

(1.中国特种飞行器研究所，湖北荆门 448035;2.哈尔滨工程大学船舶工程学院，黑龙江哈尔滨 150001）

舰船水下爆炸冲击环境实用建模方法

孙 丰1，吴 彬1，王 喆1，白兆宏2

(1.中国特种飞行器研究所，湖北荆门 448035;2.哈尔滨工程大学船舶工程学院，黑龙江哈尔滨 150001）

梁单元方向点的定义和流场大小和其单元尺寸的选取一直以来都困扰着船体建模工作者。本文提出两点适合工程应用的实用建模方法，旨在尽量减小前处理过程中的人为误差，提高仿真精度。本文首先对流场大小和单元尺寸的选取提出依据，然后提出“远距”法简化梁单元方向点的定义。经验证，文中提出的方法都取得了较好的简化效果。

模型简化;标准化;水下爆炸;冲击环境

0 引言

作为当前科学研究的主要方法之一，数值仿真用于理论验证、实验对比，在科学技术发展领域和工程应用领域内发挥了巨大作用。随着计算机硬件系统和仿真算法的快速发展，数值计算结果的精度不断提高，在解决一些相对简单的问题时，用数值计算结果可以替代真实解和实验值，可节约大量的人力、物力和财力［1］。

保证仿真计算精确的前提是建立足够精细的有限元模型。舰船一般在几千吨到几万吨不等，结构复杂尺寸巨大且包含大量设备，对于此类大型结构仿真前处理过程所消耗的资源要远大于后处理，因此提高前处理工作效率十分必要。本文对水下远场非接触爆炸问题中的舷外流场的大小和单元尺寸的选择进行讨论，并针对大量的梁模型引入的定义大量方向点问题提出了“远距”法的简化方法，分析了不同舷外流场模型和“远距”法定义的方向点距梁单元的距离对计算精度和计算时间的影响，在保证一定精度的前提下提出几点简化模型的方法，尽量提高前处理工作效率，为工程实际问题做参考。

1 水下远场爆炸中流场的建模方法

远场水下爆炸过程中，外流场大小及其单元尺寸对计算结果的影响很大。本节深入研究远场水下爆炸中外流场尺寸及单元大小对舰船冲击响应的影响，综合考虑计算精度和计算时间等因素决定流场大小及其单元大小，确定一套通用性较强的舷外流场建模方法和网格划分方法。

1.1 单元尺寸的选取

冲击波的精确传播是影响计算精度的重要因素，流场单元尺寸对冲击波的传播有较大影响。根据文献［2］单元最大长度Lmax是冲击波的最大频率的函数，即

式中:c为冲击波在材料中的传播速度;n为一个冲击波波长内的单元个数，一般不应少于6个;fmax为冲击波的上限频率，等于脉宽的倒数。

以下主要研究流场大小对舰船冲击响应的影响，选取冲击因子为0.32的计算工况，药包位于模型中部正下方。流场单元尺寸按式(1）划分为0.1 m，可保证每个波长内含有的单元不少于6个;与之相匹配的结构单元大小也为0.1 m。

1.2 流场大小对低频响应的影响

舷外流场大小会改变舰船自振时的附连水质量，从而影响舰船在水下爆炸载荷作用下的冲击响应。Blevins［1］推导了无限长圆柱壳在无限长圆柱形流场中附连水质量的解析解。表1给出了附加质量率r随流场半径的变化关系，其中附加质量率表示有限元模型在有限域流场中附连水质量与在无限域流场中附连水质量的比值。

表1 附加质量率与流场半径关系Tab.1 The relation of added mass and fluid field radius

从表1中看出，随着流场半径的增加，附加质量率越来越小，即附加质量越来越接近真实值。但是随着流场半径的增大，网格数量会急剧增加，计算耗时量也随之增大。当流场半径由6倍半宽增加到8倍时，计算精度变化不大，但网格数会成倍增加，必然导致计算时间大增。因此综合考虑计算精度和计算时间，认为流场半径与结构半宽比为6时可以足够精确的计算带有附连水质量的舰船湿模态。

设流场半径为R，结构半宽为R0，定义β为二者的比。对 β =2，3，4，5，6 的外流场进行建模，并应用ABAQUS自带算法进行固有频率的计算。计算模型为一细长半圆柱壳，有限元模型如图1所示。对各工况下前3阶湿模态进行统计，如表2所示。

图1 加筋圆柱壳有限元模型Fig.1 Stiffened cylinder shell FEModel

表2 湿模态统计Tab.2 Wetmode statistic

对比表1和表2可以看出，随着流场半径的增大，附连水质量越来越小，垂向振动频率越高。并且流场半径越小时，流场尺寸对垂向振动频率的的影响较大，随着流场半径的增大，垂向振动频率的变化率减小，逐渐趋于平缓。

在实际工程领域，流体介质具有可流动性，但在ABAQUS中采用声固耦合法计算水下爆炸问题时，外流场被模拟为一整块固定大小的声学介质，只能传播冲击波而不能流动且边界被固定，使得船体振动时由于流场过小能量无法传递出去，结构只能在有限的空间内振动，增大了振动阻尼，降低了耦合振动频率。体现为附连水质量的增加，随着流场半径的增加，流场边界的固定对船体振动的约束变小，振动频率变大附连水质量减小并趋于真实值。综上分析可知，流场半径与结构半宽比为6时，认为计算的湿模态满足工程应用。

1.3 流场大小对高频响应的影响

以β=6的流场为参考，利用图2模型，研究流场大小对高频响应的影响，计算工况同上，冲击因子为0.32，药包位于模型中部正下方。由于模型具有对称型，因此只考察模型的1/4冲击响应即可，考察点编号和位置如图3所示。考察点1处的加速度时历曲线如图4所示。

图2 有限元模型Fig.2 FEmodel

图3 考察点位置Fig.3 Check point location

图4 考察点1的加速度曲线Fig.4 Acceleration curve of check point1

如图4所示，在5个不同大小的流场中，考察点1处加速度时历曲线的变化过程几乎相同。提取其他考察点的加速度曲线也得到相同的结论，说明流场尺寸对考察点处的加速度变化过程影响不大。根据所提取的各考察点处的加速度数据，计算各考察点的谱速度。以参考流场为对比，统计不同流场大小工况中各考察点谱速度的相对误差、所有考察点的平均误差和总的计算时间，结果如表3所示。可知随流场半径的增大，相对误差和平均误差均不断下降，当流场半径与结构半宽比为5时，相对误差的变化率已经很小(见图5），但计算时间和单元数量却显著增加。

表3 谱速度相对误差和计算时间Tab.3 Relative error of spectra velocity and computation time

图5 相对误差随流场大小变化曲线Fig.5 Relative error versus fluid field radius curve

根据表3中的平均相对误差和计算时间作图6，给出了计算时间和计算精度的关系。从图中可看出，随着计算精度的提高，计算时间逐渐增加。曲线的变化率最大阶段对应了β=4的工况，也就是说当大于4时，提高计算精度的同时计算时间的增加量更大。

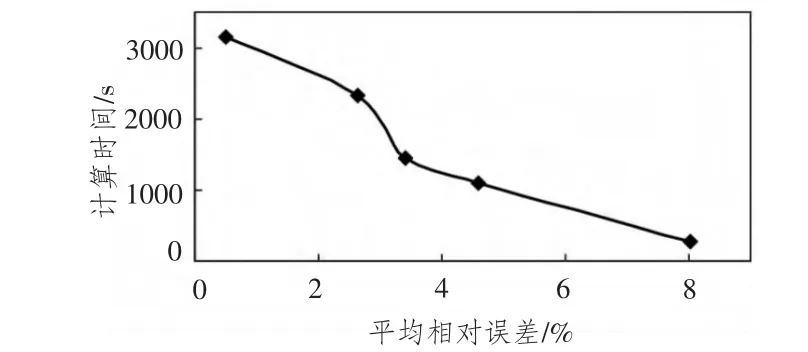
图6 计算时间随相对误差变化曲线Fig.6 Computation time versus relative error curve

所以当流场半径与结构半宽比为4时，认为在获得较高计算精度的同时耗费了较少的计算时间。

2 梁单元方向点的简化定义方法

舰船结构中存在大量的梁结构，因此会导致有限元模型中梁单元数量巨大，标准的建模方法是为每根梁指定一个方向点，由于工作量巨大，会耗费大量的时间。对于船体结构由于其形状不规则，将导致曲面上梁的方向难以确定，由于方向点的数量太多，定义方向点编号时易出错，这些问题都降低了前处理过程的工作效率，因此本文提出“远距”法简化梁单元方向点的定义方法。

2.1 “远距”法有效性检验

远距法的基本思想是选择一个相对较远的点作为一类朝向相近梁的方向点，这样的梁多是在一块板上朝向同一侧。本文选取一个带有加筋的横舱壁作为研究对象，用来检验“远距”法的有效性。横舱壁模型的主尺度如图7所示。

图7 横舱壁模型Fig.7 Bulkhead model

为分析远距法方向点位置对结构强度的影响，建立以下4个不同位置方向点的模型:

Model－1:为计算模型上每根梁分别定义1个方向点，此时有限元模型最接近真实模型。这是标准的定义方向点的方法，但该方法繁琐且工作量较大。以此模型为参考模型，对另外3个简化模型进行对比分析。

Model－2:在距离横舱壁中心垂直距离L的位置定义一个方向点，作为该模型上全部梁单元的方向点。

Model－3:在距离横舱壁中心垂直距离5L的位置定义一个方向点，作为该模型上全部梁单元的方向点。

Model－4:在距离横舱壁中心垂直距离10L的位置定义一个方向点，作为该模型上全部梁单元的方向点。

其中L为横舱壁结构的宽度，L=11 m。4种模型的有限元模型如图8所示。从图中可以清晰地观察到方向点的位置对梁单元朝向的影响。

定义α为梁与舱壁之间的最小夹角:

图8 横舱壁有限元模型Fig.8 Bulkhead FEmodel

式中:D为远距法定义的方向点距横舱壁的中心的垂直距离，本文中D=L/5L/10L;L为横舱壁的宽度。最小夹角α如图9所示。Model－1中角α为90°，其他工况中角α大小和相对误差见表4。下面从静载荷作用下结构响应和结构模态2个方面考察“远距”法对结构强度的影响。

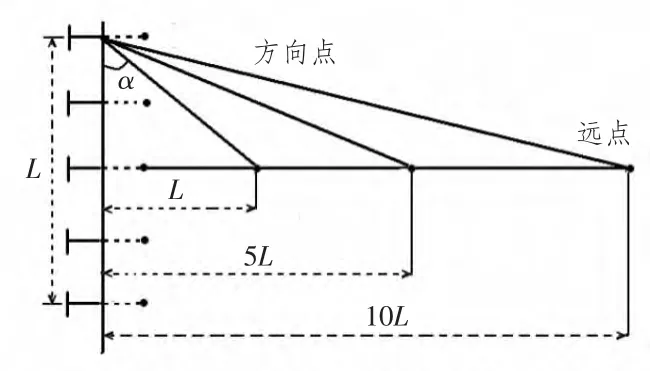
图9 角α示意图Fig.9 Angleαsketch map

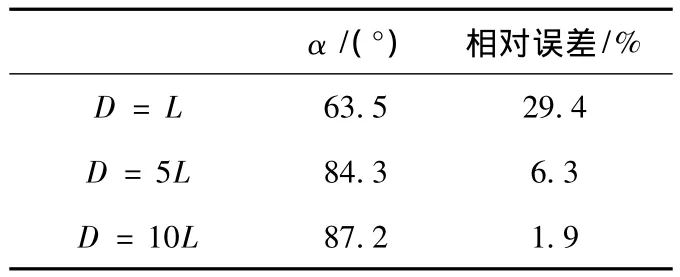
表4 偏转角α的相对误差Tab.4 α's relative error

2.1.1 静载荷作用下结构响应

根据文献［3］对潜艇横舱壁强度校核，取静载荷为10 000 Pa。横舱壁四周的边界条件为刚性固定，分别从结构变形、最大位移和应力3个方面响应考察4种横舱壁模型的强度。

Model－1～Model－4的结构变形云图如图10所示。为清楚地观察变形情况，将结构变形放大了100倍。

图10 结构变形Fig.10 Structure deformation

从图中可以看出，4个模型的结构变形相似。提取模型的最大变形和最大应力如表5所示。

表5 最大变形和最大应力Tab.5 Max deformation and max stress

从表5中看出，随着方向点距舱壁中心距离的增大，最小夹角α逐渐增大并趋于90°，最大变形和最大应力的误差不断减小。当D=10 L时，结构最大变形和最大应力误差均小于0.07%，可以预见随着方向点距离的增加，相对误差会不断减小，验证了远距法的有效性。

2.1.2 模态分析

由于梁单元的方向的改变并不会引起结构质量的改变，但会对刚度产生一定的影响，因此通过分析4种模型模态的差别可以看出方向点的改变对结构刚度产生的影响。根据公式ωn=可以求解系统的固有频率，其中K为结构刚度，M为结构质量。图11所示为Model－1的前3阶模态振型。

图11 Model－1前3阶模态振型Fig.11 The first threemode of Model－1

统计4个模型的前3阶垂向自振频率，并与参考模型进行对比计算相对误差，如表6所示。

表6 横舱壁前3阶垂向固有频率Tab.6 The first three inherent frequency of bulkhead

从表6可知，若梁单元方向不与面板正交，横舱壁垂向刚度会减小。随着梁单元方向与面板最小夹角α趋于90°，相对误差会逐渐减小。当方向点与舱壁中心距离在舱壁宽度5倍以上时，相对误差已经足够小可以忽略不计。远距法可以很大程度上节约建模时间，只要方向点距离结构足够远就可以达到相当高的计算精度。

4 结语

本文针对船体结构建模过程中存在的不确定性问题进行分析，以工程实践为基础，兼顾计算时间和计算精度，对不同的建模方法和模型简化方法进行对比分析，主要得出以下结论:

1）适当选取流场尺寸对分析舰船冲击响应至关重要。采用声学单元模拟舷外流场，与真实物理流场不同，流场边界固定且流体介质不能流动。分析结果表明，流场半径越小，附连水质量越大;随着流场半径的增加，附连水质量逐渐下降并趋于真实值。综合考虑认为流场半径与结构半宽比为6时，既能保证模态分析的准确性，又能较准确的计算结构响应。

2）远距法可大大减少建模过程中定义梁单元方向点的工作量。通过静力分析和模态分析两方面验证了远距法的正确性，当方向点与舰船的垂直距离大于10L时 (L为船长），远距法对整船刚度的影响可以忽略不计。

［1］BLEVINSR D.Formulas for natural frequencies and mode shapes［M］.Reissue Edition.Krieger Publishing Company，1979.

［2］郭君.加筋双层筒形结构冲击环境特性研究［D］.哈尔滨:哈尔滨工程大学，2005.

［3］COLE R H.Underwater explosions［M］.Princeton University Press，1948.

［4］姚熊亮，李克杰，张阿漫.水下爆炸时舰船正交异性板的简化方法研究［J］.中国舰船研究，2006，1(3）:30 －37.

［5］殷玉梅，赵德有.船舶与海洋工程结构物振动分析中的设备实用建模方法究［J］.中国海洋平台，2006(6）:28－32.

［6］ABAQUS Analysis User's Manual，Hibbitt，Karlsson and Sorensen，2004.

［7］JIN Qian-kun，DING Gang-yi.A finite element analysis of ship sections subjected to underwater explosion［J］.International Journal of Impact Engineering，2011，38:558－566.

Primary investigation of warship shock environment practicalmethod under far field underwater exp losion

SUN Feng1，WU Bin1，WANG Zhe2，BAIZhao-hong2
(1.China Special Vehicle Research Institute，Jingmen 448035，China;2.College of Shipbuilding Engineering，Harbin Engineering University，Harbin 150001，China）

The orientation definition of beam elements and the choices of fluid and its elements size alwaysmake trouble to themodel builders.This paper puts forward two kinds of Practicalmethod for engineering aimed atminimizing human error and improve simulation precision.First，the accordance of fluid field is put forward in element size and fluid field radius;Last，the far pointmethod is given to define the orientation point of beam element.By checking，themethods given in this paper havemade a considerable effect.

model simplification;practicalmethod;underwater explosion;shock environment

U663.2

A

1672－7649(2014）04－0022－05

10.3404/j.issn.1672－7649.2014.04.004

2013－03－26;

2014－03－03

国家自然科学基金青年科学基金资助项目(51109042），黑龙江自然科学资助基金资助项目(E201124），中国博士后基金资助项目(2012M520707）

孙丰(1988－），男，硕士，主要从事船舶结构冲击动力学研究。