三次参数样条曲线恒线速插补的研究
李勇波,裴雪丰
(中国地质大学 (武汉)机械与电子信息学院,湖北武汉 430074)
三次参数样条曲线恒线速插补的研究
李勇波,裴雪丰
(中国地质大学 (武汉)机械与电子信息学院,湖北武汉 430074)
针对非线性曲线轮廓的插补,在数据采样插补的基础上,研究三次参数样条曲线恒线速插补方法,并通过构建OpenGL渲染环境,对数据进行仿真,完成了曲线恒线速插补的G代码设计,实现了复杂零件轮廓的插补。
三次参数样条曲线;恒线速插补;OpenGL
由于样条曲线的二阶连续性,在具有复杂轮廓的曲面机械加工中,其实现方法得到广泛研究,其参数化实现是国内外数控和CAD/CAM技术的研究热点[1-3]。复杂零件轮廓的加工实现,传统的做法是通
过微小直线段来逼近曲面轮廓,为了满足精度要求,直线段取值很小,造成NC代码量大的问题。为了满足复杂曲线高速、高精度加工要求,在分析数控系统数据采样插补方法的基础上,研究了样条曲线的参数实现方式,并对参数方程进行微分处理,实现恒线速插补。插补实现原理如下:在已知曲线控制点坐标的前提下,将曲线分段,分别求出相邻两点之间的曲线
参数方程;由进给速度计算每个插补周期的进给量,由恒线速原理计算各轴向进给量,送给伺服系统实现插补。
1 三次参数样条曲线的构造
数控系统中数据采样插补在以直流或交流电机为执行机构的闭环和半闭环位置采样系统中应用较多。
三次样条插值方法数值稳定性好,曲线具有一阶、二阶导数连续的性质,精度与样条函数的次数无关[4]。但也存在其局限性,如不能模拟大挠度曲线、依赖于坐标系的选择、缺乏几何不变性等,采用参数曲线可克服上述问题[5-7]。
1.1 参数函数方程求解
对给定的一组控制点Q0,Q1,…,Qn,假设曲线由n段r(t)拼接而成。


1.2 恒线速插补实现
由上节求出参数样条曲线方程,恒线速插补即在曲线切线方向上单位进给量不变,令单位进给量为DIV。如图1所示,图中的点C和点D之间通过两个插补周期即可完成,以两段直线段来代替曲线段。

图1 插补示意图

Δx,Δy即为每轴单位时间内的插补进给量,曲线切线方向的单位进给量d s(t)=DIV保持恒定。
2 数控系统中样条曲线实现
2.1 样条曲线数据仿真
样条曲线在数控领域应用比较广泛,以电子凸轮为例,传统的机械凸轮是通过凸轮实现非线性的加工轨迹,而电子凸轮则直接将轨迹点输入到驱动器内,方便根据需求更改曲线,并且没有机械凸轮的磨损。
例如加工出如图2所示凸轮中间轮廓,按照轮廓参数要求设定控制点坐标 (以圆心为坐标系原点),采样12个控制点 (单位mm):


图2 凸轮
为了验证计算结果的正确性,通过OpenGL对计算的数据进行仿真。OpenGL是个专业的图形程序接口,通过调用底层图形库实现绘图,同样应用在数控仿真领域[8]。按照一定的步骤在VC++6.0开发环境下进行配置[9],令DIV=10.0 mm。按上述方法计算每段曲线的参数方程,通过恒线速处理,得到各轴向每段时间的单位时间进给量xi(t),yi(t)并描绘出来,仿真曲线如图3所示,改变DIV=5.0 mm,插值点的个数增加,见图4。
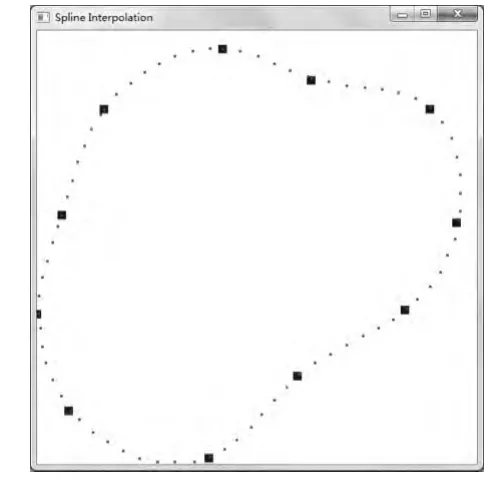
图3 OpenGL仿真图(DIV=10.0mm)
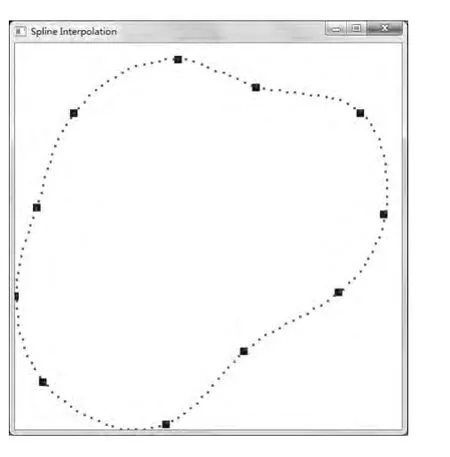
图4 OpenGL仿真图(DIV=5.0 mm)
图3中标注的为控制点,其余为插值点,控制点按照在曲线上的顺序依次赋值。图5为AutoCAD所绘的非闭合样条曲线图 (拟合公差为0)。对比3个图可知:用该方法得到的参数曲线通过微分处理后,将曲线分成若干小直线段,通过设置DIV来调节小直线段,进而提高精度。

图5 AutoCAD所绘的非闭合样条曲线图
2.2 样条曲线G代码的实现
分析上述样条曲线可知,所需参数如下:控制点各轴坐标、插补周期、进给速度。
在数控系统中将各控制点坐标存储在用户变量中,起点为上节G代码的结束点;插补周期在以数控采样插补为主的系统中为恒定值;进给速度由用户定义,可以更改。因此可定义如下G代码格式:

其中:G06为自定义G码,可以设为其他值;Q、E分别是控制点坐标的起始、结束地址;D为坐标指定方式 (0绝对或1相对);A、B为样条曲线结束点坐标值;F为进给速度。
设置以上G代码格式,其执行流程如图6所示。

图6 样条曲线执行流程图
将OpenGL仿真程序稍做更改,移植到数控系统中进行描图,并进行测试。将上述采样数据点保存在起始地址为1000的变量中,测试G码如下:


根据数控器程式预览功能,得到如图7所示的描图轨迹。

图7 样条曲线测试图
从测试可知:该方法有效地描绘了复杂曲线的轨迹,测试程序简单,可移植性强。
3 总结
综上所述,采用建立三次参数样条曲线方程的方法,在已知复杂曲线关键控制点的前提下,仿真效果明显,并在实际数控系统中得到应用。
[1]盖荣丽,王允森,孙一兰,等.样条曲线插补方法综述[J].小型微型计算机系统,2012,33(12):2744-2748.
[2]黄建,宋爱平,陶建明,等.一种三次插值样条曲线的插补方法研究[J].现代制造工程,2012(4):46-49.
[3]LIN Bin.Parametric Cubic Spline Method for the Solution of the Nonlinear Schrodinger Equation[J].Computer Physics Communications,2012(2):60-65.
[4]李庆扬.数值分析[M].北京:清华大学出版社,2008.
[5]张彩明.高精度三次参数样条曲线的构造[J].计算机学报,2002,25(3):262-268.
[6]MOHANTY R K,JAIN M K,DHALL Deepika.High Accuracy Cubic Spline Approximation for Two Dimensional Quasi-linear Elliptic Boundary Value Problems[J].Applied Mathematical Modelling,2012(2):155-171.
[7]FYFED J.The Use of Cubic Splines in the Solution of Twopoint Boundary Value Problems[J].Computer Journal,1969,12(2):188-192.
[8]李琳茹,游林儒,刘少君.利用OpenGL实现数控系统加工过程的三维动态仿真[J].组合机床与自动化加工技术,2012(1):62-65.
[9]王正强.OpenGL在VC++6.0开发环境下的编程实现[J].软件技术,2011(1):89-91.
Research on Constant Linear Velocity Interpolation of Parametric Cubic Sp line
LIYongbo,PEIXuefeng
(College of Mechanical& Electronic Information,China University of Geosciences,Wuhan Hubei430074,China)
In order to realize nonlinear curve contour interpolation,how to achieve constant linear velocity interpolation was discussed for parametric cubic spline and OpenGLwas used to do some data simulation based on data sampling interpolation,then G code of constant linear velocity interpolation was designed.Interpolation of outline of complex partswas completed.
Parametric cubic spline curves;Constant linear velocity interpolation;OpenGL
TP29
A
1001-3881(2014)10-025-3
10.3969/j.issn.1001-3881.2014.10.007
2013-04-16
李勇波 (1967—),男,硕士,副教授,研究方向为机电一体化与自动控制。E-mail:13986290039@139.com。

