不定积分解法研究
李明
(苏州工业职业技术学院,江苏 苏州 215104)
不定积分解法研究
李明
(苏州工业职业技术学院,江苏 苏州 215104)
不定积分形式千变万化,这种形式上的多变和易变给高职学生解题带来非常大的困难,面对高职学生现状和特点,立足基础,归纳基本方法,通过对比增强解法间的区分度,帮助学生快速准确地选择积分方法,激发学生的学习兴趣,增强学生的自信心,在此基础上,展开有意的思维拓展才是有效的.
不定积分;积分方法;解法研究
极限、导数和积分是微积分的三大概念,极限是导数和积分的基础,导数与积分是互逆运算.积分中不定积分的概念不抽象也不难理解,但公式多且形式千变万化,而高职学生的数学基础比较薄弱,缺乏分析问题和解决问题的能力,不会对知识进行有效迁移,造成了学生学完不定积分的各种解法后仍不知所措.经多年教学总结发现,学生并非未掌握各种解法,而是面对积分的众多解法及解题思路时,混淆了解法之间的区别所致,针对这样的情况,总结积分类型,罗列对应解法,通过对比加强解法间的区分度,帮助学生快速准确地选择积分方法,是解决这一困境的有效办法[1].
目前,高职院校高等数学课程中所传授的不定积分解法有四种,分别是直接法、凑微分法、变量代换法和分部积分法.每一种解法都是为了解决一个难点而产生的.
1 直接法
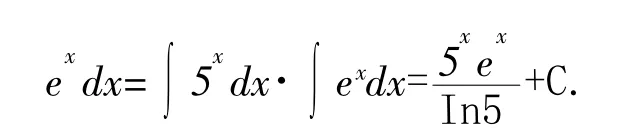
分析错解的原因:(1)积分只有加减法法则,没有乘除法法则;(2)被积函数是幂函数,属于基本初等函数,只要被积函数属于基本初等函数都可以通过16个公式直接得到结果.因此,会背公式,但不分析16个基本公式被积函数的特点,也很难做到应用自如.
2 凑微分法
凑微分法需要使用化简、变形,然后才能使用公式,知识难度大,解题需要较高的技巧和积累,学生往往感觉无从下手,不知所措,教师需要做到以下几个方面:
(1)对比法.所谓对比法是与错例展开对比,加强区分度,总结出常用凑微分式子.表1所列内容是搜集了学生平时易错易混淆的知识点,通过对比法教学,能较大程度减少学生学习凑微分的困难,提高教学效果.导数与积分互逆,这样的对比可以从导数与积分的16个基本公式中列举出更多.
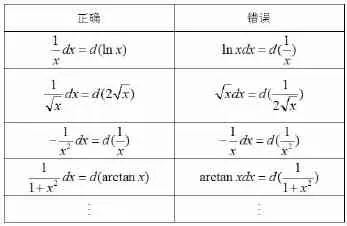
表1 凑微分正误对照表
(2)逐次凑微分法.所谓逐次凑微分法是针对需要两次及两次以上使用凑微分公式的,具有较大难度凑微分问题的解决办法.如
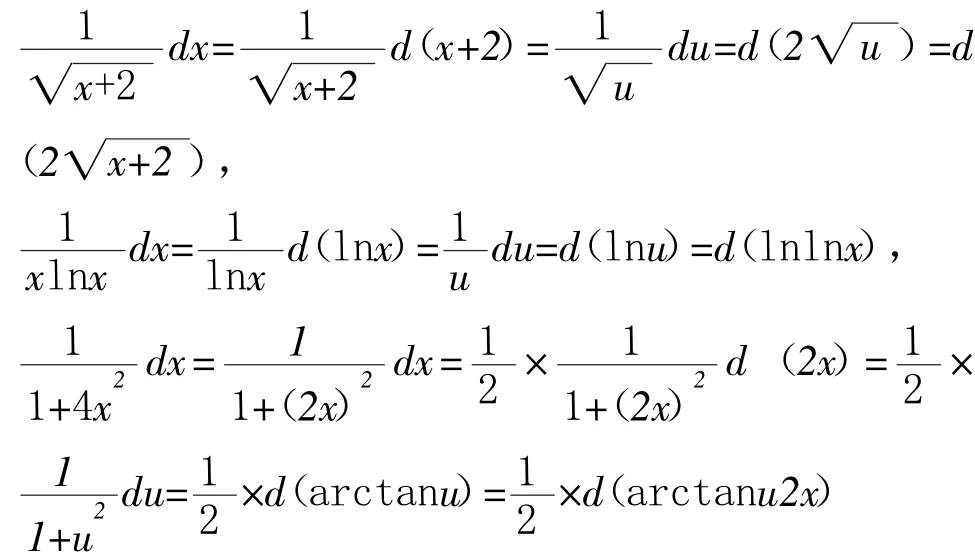
(3)整体代换法.所谓整体代换法是一种整体意识的表现形式,是将被积函数(或被积函数中的某因子)看成一个整体,使得凑微分后,微分因子也具有相同的式子,可达到整体代换的目的.如
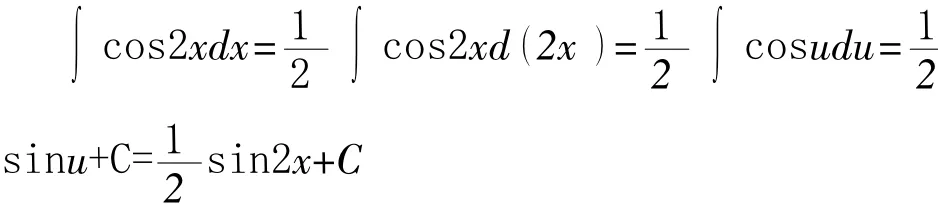
解析:以基本公式∫cos xdx=si n x+C为参考,较容易得出将cos2x中的2x看成一个整体,凑微分后,微分符号d后也要凑成2x这个整体,自然有凑微分式子dx=d( 2x ),然后做整体代换u=2x即可得出正确的结果.再如,
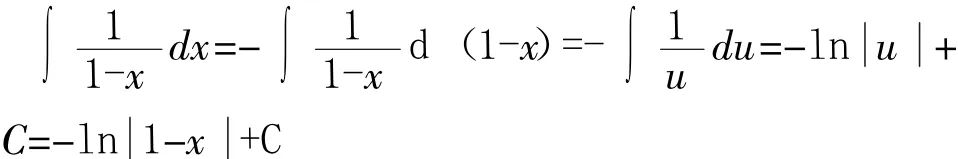
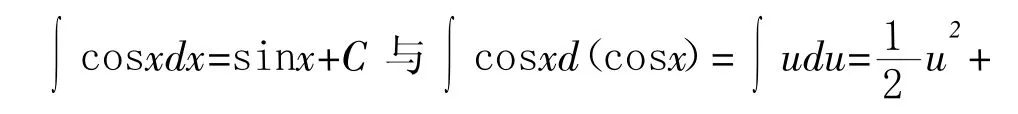
(4)类型辨别法.所谓类型辨别法是将被积函数按函数类型分类进行解法归纳的一种方法.
类型Ⅰ被积函数为有理分式,归纳为以下四种解法:
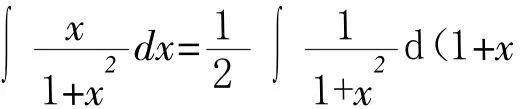
第一种解法:直接凑微分,此时被积函数中含有明显的可凑微分因子,如
cosxdx=d(sinx),secxtanxdx=d(secx),sec2xdx=d (tanx)等等.
第二种解法:利用三角恒等式关系,如
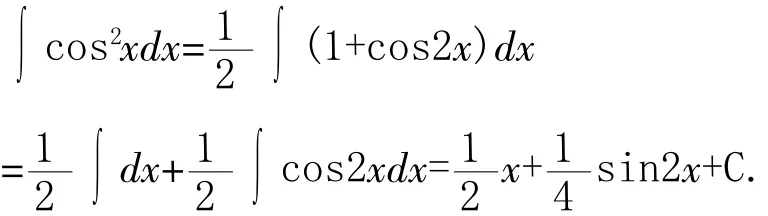
以上例子的被积函数具有较大的相似度,但是方法确相差较大,这些例子的讲解过程,也较好地实施了对比和反差,为后期学习打下了坚实的基础.
3 变量代换法
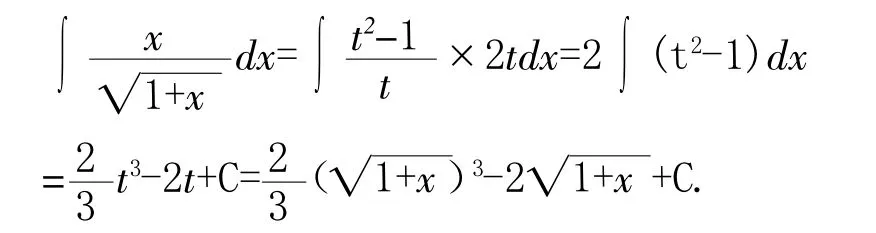
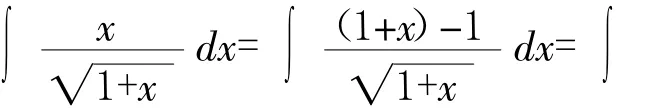
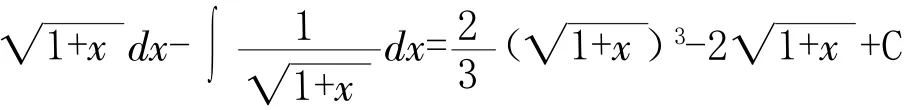
此解法是需要学生对积分知识的积累,更需要学生的思维拓展,以及对积分各种解法的熟练掌握.
4 分部积分法
分部积分法是教师实施错误体验教学的绝佳环节.其基本原理是∫udv=uv-∫vdu,主要解决被积函数是两个函数相乘的形式,解法与u的选取有关,u选择对了,分部积分也就成功了.而u的选取过程教师应该让学生体验错误,经历了错误,才知道选择正确的方法是什么,从而才能得到u应遵循以下规律,见表2[2]
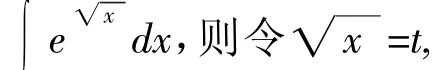
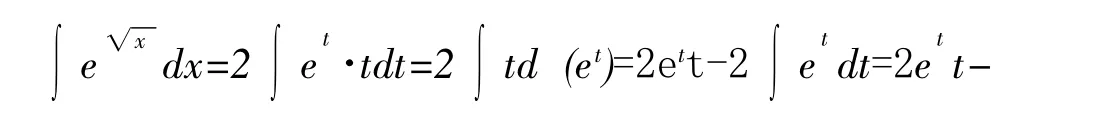
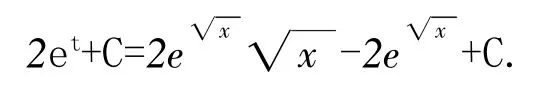

表2 分部积分法中u的选取规律
5 结束语
虽然不定积分定理少,但公式多形式复杂,千变万化,这种形式上的多变和易变给高职学生学习带来非常大的困难,面对高职学生现状和特点,立足基础,归纳基本方法才能激发学生的学习兴趣,增强学生的自信心,在此基础上,展开有意的拓展才是有效的[3].
[1]吴凤珍.不定积分教学研究[J].兰州教育学院学报,2013, 29(4):71-73.
[2]许艾珍,黄莉萍,李明.高等数学应用教程[M].北京:航空工业出版社,2010.
[3]段馨娜.不定积分的题型归纳[J].吕梁教育学院学报,2013,30(1):96-98.
Indefinite Integral Method Research
LI Ming
(Suzhou Institute of Industrial Technology,Suzhou Jiangsu 215104)
Indefinite integral forms are changeable and mutable which brings great difficulties to higher vocational students.Facing the present situation and characteristics of the higher vocational students basing on the foundation, this paper summarized the basic method, comparied the degree of differentiation between solution, helped students to quickly and accurately choose integral method, in order to stimulate students' interest in learning, enhance students' self-confidence.
Indefinite Integral; Integral Method; Method Research
O172
A
1672-2094(2014)05-0150-04
责任编辑:张隆辉
2014-06-18
李 明(1975-),女,苏州工业职业技术学院文化与艺术系副教授,硕士.研究方向:应用数学研究.

